高度計波高數據同化對印度洋海域海浪模式預報影響研究

齊鵬，范秀梅

（1.中國科學院海洋研究所海洋環流與波動重點實驗室，山東青島 266071；2.中國科學院大學，北京 100039）

1 引言

近年，我國海洋環境業務預報部門已建立基于第三代海浪模式的全球海浪數值預報業務化系統。但是，目前在海浪預報工作中，仍未能有效利用衛星高度計波高測量數據進行海浪的同化預報。從另一方面看，越來越多的海洋衛星通過高度計提供全球大覆蓋量、高精度和實時的海洋表面測量數據，使得將高度計實時波高觀測數據同化到海浪模式以改善模式預報初始場，進而提高海浪數值預報精度成為可能。

如上所言，海浪觀測方面，當前海洋衛星觀測已成為海洋環境立體觀測的主要手段之一。1978年，美國國家航空航天局（NASA）發射了具里程碑意義的海洋衛星SeaSat-A，它發回的數據通過處理可獲得包括海面風速、風向、波高、波長、波譜、海面溫度、大氣水含量、海冰、海面地形、海洋水準面和高分辨率雷達圖像，而且測量精度基本達到實用要求。其后，主要有歐空局（ESA）1991和1995年先后發射的資源衛星ERS-1和ERS-2；1992年NASA與法國國家空間研究中心（CNES）合作發射的TOPEX/Poseidon（簡記為T/P），其后繼衛星Jason-1于2001年底發射；2008年發射的Jason-2則是T/P和Jason-1的后繼衛星，它的發射出于以下兩個目的：一是為海洋研究提供高質量的觀測，二是為同化和預報提供業務產品。另外，值得特別指出的是，2012年4月起我國第一顆海洋動力環境衛星海洋二號（HY-2）已開始向社會發布海洋環境監測數據產品。

海浪模式方面，WAVEWATCH IIITM是由美國NCEP（National Centers for Environmental Prediction）的 EMC(Environmental Modeling Center)下面的MMAB（Marine Modeling andAnalysis Branch）在WAVEWATCHⅠ和WAVEWATCHⅡ的基礎上開發的全譜空間的第三代海浪模式。其不同之處主要體現在控制方程、程序結構、數值和物理方法方面，允許用戶用自己的數值或物理方法發展一個基于WAVEWATCH IIITM框架的新的海浪模式；同時，WAVEWATCH IIITM框架下的優化方案、并行化算法、嵌套方案、輸入和輸出功能能方便地得到共享和使用。此外，本文所用版本WAVEWATCH IIITMversion 3.14提供多網格相互作用即網格嵌套的模式方案，使得在處理有開闊水域邊界時，能使用網格嵌套方案為開邊界提供邊界條件。WAVEWATCH IIITM沒有提供可用的海浪同化代碼（雖然NCEP表示已在做海浪同化技術方面的工作，但目前并不打算發布海浪同化模塊），但提供了海浪同化的接口，這就方便我們將自己開發的同化程序植入模式和隨模式的積分運算而被調用，并將同化結果反饋到模式中，為模式預報所用。

只使用高度計波高數據的同化方法是由Esteva[1]和Janssen等[2]較早提出。Lionello等[3]認為Janssen等[2]的同化方法太復雜，提出了更簡明的方法。其方法分兩步：第一步，以實測有效波高（SWH）做最優插值分析；第二步，由浪高分析場求總波能，然后利用總波能和初估模式譜得到最終的海浪分析譜。他們是利用插入觀測法或最優插值法（Optimal Interpolation，OI）將觀測值同化到WAM（Wave Modelling）模式中。Mastenbroek等[4]，Breivik 和Reistad[5],Lionello 等[6]，Bender和 Glowacki[7]以 及Greenslade[8]應用類似方法開展同化海浪預報，均收到不同程度改進海浪預報的效果。國內方面，張志旭等[9]使用一種簡單的逐時同化的方法對海浪模式進行高度計SWH數據同化試驗；王毅和余宙文[10]將最優插值和海浪譜重構技術與SWAN模式結合，建立海浪最優插值同化預報模式。

總之，為提高海浪模式預報精度和延長其預報時效，當前，人們有條件大量使用高度計海浪觀測資料，將其同化到海浪模式以提高模式預報初始場的質量，進而提高海浪預報效果。

根據我國海洋公益性行業科研專項的要求，結合當前我國海上能源運輸安全和海軍護航任務迫切需求，特別是圍繞關于重點開展海洋環境預報中關鍵技術的研究，建立印度洋海域海洋環境數值預報系統，提升我國遠洋環境保障能力，我們研制了基于OI方法的高度計SWH數據同化并行模塊，并將其植入第三代海浪模式WAVEWATCH IIITMversion 3.14。通過同化Jason-2高度計SWH數據，實現模式邊積分邊同化的功能，進行印度洋目標區域海浪場短期預報，并對同化提高模式預報初始場的質量和同化對短期預報影響的效果和時效性進行檢驗。

2 高度計有效波高OI同化模塊研制

最早，Eliassen[11]利用最小二乘法推導觀測值和背景場向量的OI方程。在對背景場和觀測誤差性質充分了解的基礎上，OI方法充分利用背景場和觀測值的信息，給出一個方差最小意義下的最優線性估計。式（1）和（2）為OI同化表達式。

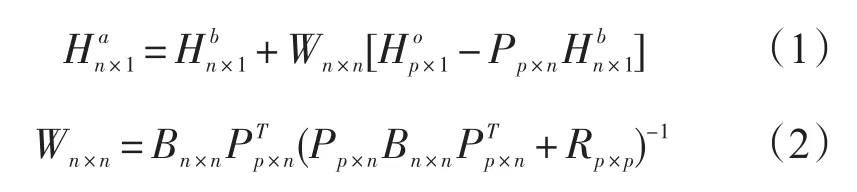
式中，各下標代表矩陣的維數，n表示所有點數，p表示觀測點數；上標a代表分析場，也即加入同化后的模式波高場；b代表背景場，也即同化之前模式給出的（待同化的）波高場；o代表觀測場；矩陣H代表有效波高；P是觀測算子，它是一個插值算子（本文的插值方法為雙線性插值），作用于背景場Hb，可以得到觀測值的第一猜值PHb；W代表最優權重矩陣；R代表觀測誤差協方差矩陣；B代表背景誤差協方差矩陣。

對于觀測誤差協方差矩陣R，與國內外同類研究的做法一樣，這里R中元素的值取為：

式中，δkj是kronecker符號；σ0的取值，根據Jason-2產品手冊中給出的高度計有效波高誤差為5%或0.25 m，同時考慮文中所用觀測時次的有效波高大都在5 m以內，故取σ0=0.25。易知，這里R事實上是一個p×p維的常值對角方陣，即不同點上觀測值之間是不相關的。

對于背景誤差協方差矩陣B，與國內外同類研究的做法一樣，根據相關長度法，其元素的值采用下面的經驗表達式：

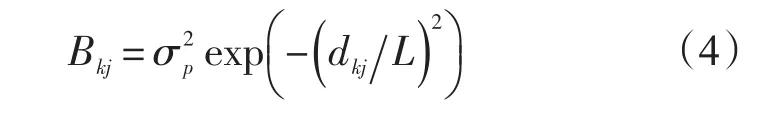
式中，σp是模式預報的背景場的均方根誤差（RMS），并參考已有的業務化預報結果，這里σp取為0.6 m；dkj是觀測點k與 j之間的距離，以度為單位。L為經驗常數，根據相關文獻，取L=8Sx，Sx為模式的空間網格分辨率，本文取為1/3°，故L約為2.67°；換算成以km為單位，則L在300 km左右。通過試算同化效果，將L值調整到相對較為合理。

計算背景誤差時，還需考慮兩點的背景方差能相互影響的最大距離，即影響半徑的問題。文中影響半徑r的取法為r=11Sx，即約為400 km。最后，B矩陣中的元素由下式得到：

由式（5）可知，兩點之間的距離如果大于影響半徑r，就認為它們之間的背景方差不相關。在OI同化方法中，觀測誤差協方差和背景誤差協方差對同化效果至關重要。因而，不排除為了同化的效果更好，不同海區在參數選取上可有不同，一般通過試算，可以獲得一個較合理的參數設置。

在處理占用內存較大的背景誤差協方差矩陣時，文中采用稀疏矩陣的表示方法，對稀疏矩陣的計算則采用專門處理稀疏矩陣的Sparse Blas函數庫里的函數，以提高運算速度。

完成上面工作后，接下來要做的是使編寫好的OI同化模塊與WAVEWATCH IIITM模式實現對接。值得指出的是，這里開發的同化模塊也是按并行設計的，這樣就與要植入其中的海浪模式在程序并行風格上取得了一致。

WAVEWATCH IIITM由模塊ww3_shel控制整個模式的運行（見圖1），而w3wavemd是模式的核心計算模塊；調用同化模塊是在模式積分到目標時刻，輸出結果之前，被調用；同化完有效波高數據后，調用輸出模塊，輸出同化后的模式結果（見圖 1）。

作為全譜空間模式，WAVEWATCH IIITM模式中的海浪是以二維波譜形式出現，而被同化的是高度計的有效波高，由此需要在每次同化過后利用同化后得到的有效波高分析場重構出相應的二維海浪譜。同化前與同化后的波能表達式如下：

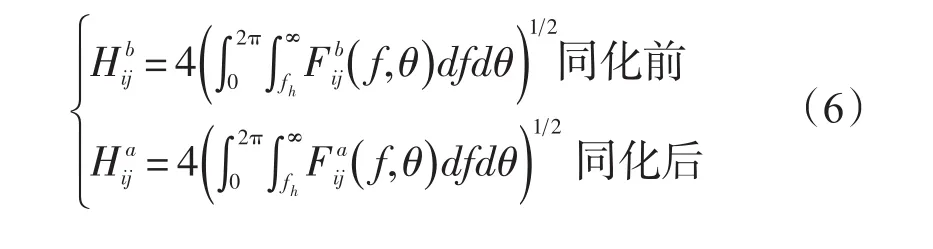
式中，i、j為網格點坐標；上標b和a分別代表同化前和同化后；Hij代表有效波高，Fij(f,θ)代表海浪二維波譜；f是海浪頻率，θ是波向。在有效波高的變化不會引起波能在頻率和方向上的重新分布，而只會引起波能在譜空間中相同的線性變化的假定下，由上面同化前與同化后的波能表達式可以得到同化后的海浪譜調整形式為：

在使用Jason-2高度計有效波高（SWH）數據時首先需要對數據進行質量控制，即剔除不合理的異常數據。此外，我們在同化數據選取時規定，取計算范圍內有觀測數據的時刻作為同化時刻，以此時刻為中心，在其±0.5 h時間范圍內取觀測數據，作為該時刻同化所采納的數據，這樣基本上可保證同化時刻觀測值與模式輸出值在時間上取得一致，從而保證同化效果。本文同化2010年12月15—17日期間Jason-2在北印度洋海域上空軌道線上高度計測量SWH（見圖5），得到同化初始場，并以此做2010年12月18—20日3天的海浪預報。前后6天對應的衛星軌道周期號是Cycle90。

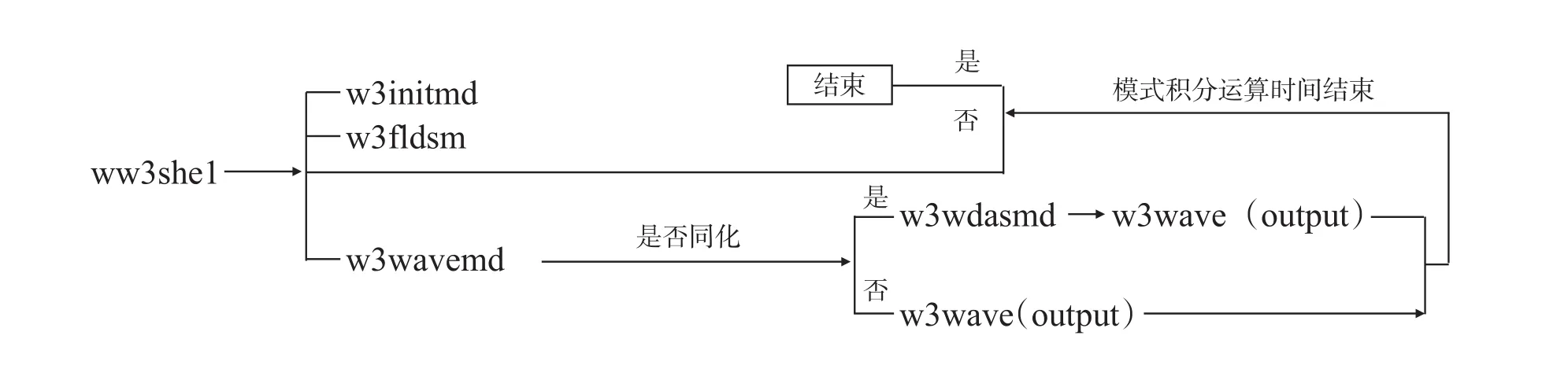
圖1 植入同化模塊的WAVEWATCH IIITM流程圖

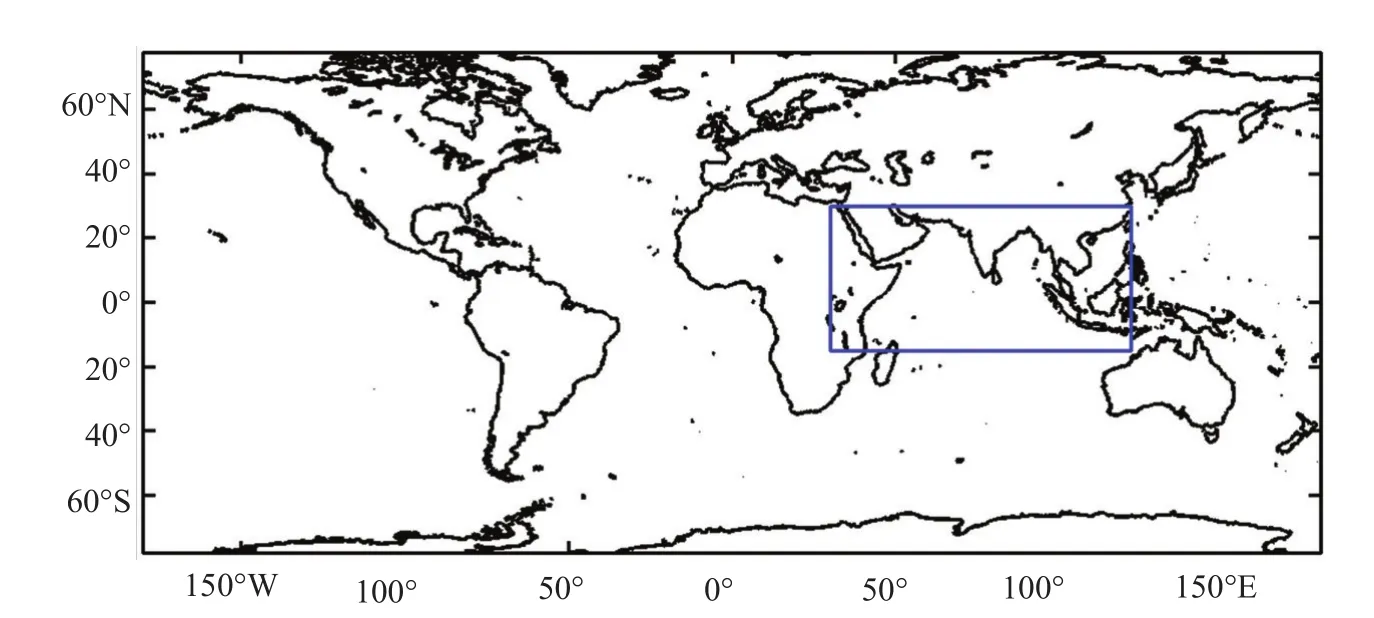
圖2 網格嵌套模式方案

3 高度計SWH同化初始場的檢驗

為檢驗上述高度計SWH數據同化模塊用于WAVEWATCH IIITM得到的同化初始場對比無同化的情形，對模式初始場是否有改善以及改善程度，設計了以下數值試驗。以5°S以北印度洋海域作為目標計算區域，即5°S—25°N，40°—105°E；空間網格分辨率取1/3°×1/3°；海浪譜網格分辨率取24個方向（即方向分辨率為15°）,和25個頻譜段，即按公式fm=αfm-1，這里，m=1,2,···,25 ，初始頻率 f0取0.0418，頻率增長因子α取1.1。海面大氣強迫采用業務預報單位提供的WRF（Weather Research and Forecasting）模式的海面10 m風場產品，1 h 1次的。

考慮目標計算區域南邊界連接開闊大洋，極易受傳入大洋涌浪信號影響，采用全球網格嵌套印度洋區域網格的方案（見圖2），為其提供開邊界條件。全球網格計算范圍：78°S—78°N，180°W—180°E；所給空間網格分辨率相對較低：1.0°×1.25°；海面大氣強迫采用6 h1次的NCEP再分析風場。全球網格模式中的頻譜和方向譜參數設置與嵌套其中的區域網格的一致。

WAVEWATCH IIITMversion 3.14提供了多網格嵌套的模式運行功能。采用嵌套方案后，由ww3_multi模塊替代ww3shel（單網格模塊）管理和調用其它的函數，完成多網格嵌套后的模式積分。

2010年12月15—17日這3天在目標計算區域有Jason-2高度計測量數據的時刻列于表1，數據同化即發生在這3天中有觀測數據的那些時刻。

首先，我們檢驗利用同化數據生成同化分析場的效果。我們將同一時刻同化模式的結果（SWH）、無同化的模式結果（SWH）分別與高度計測量SWH進行比較（見圖3）。圖3為沿軌比較，容易看出，同化模式的結果與高度計SWH更接近。

表1 用于同化的高度計波高數據所在時刻

表2 同化和無同化的模式SWH分別與高度計測量SWH之間的統計檢驗(2010年12月15—17日)

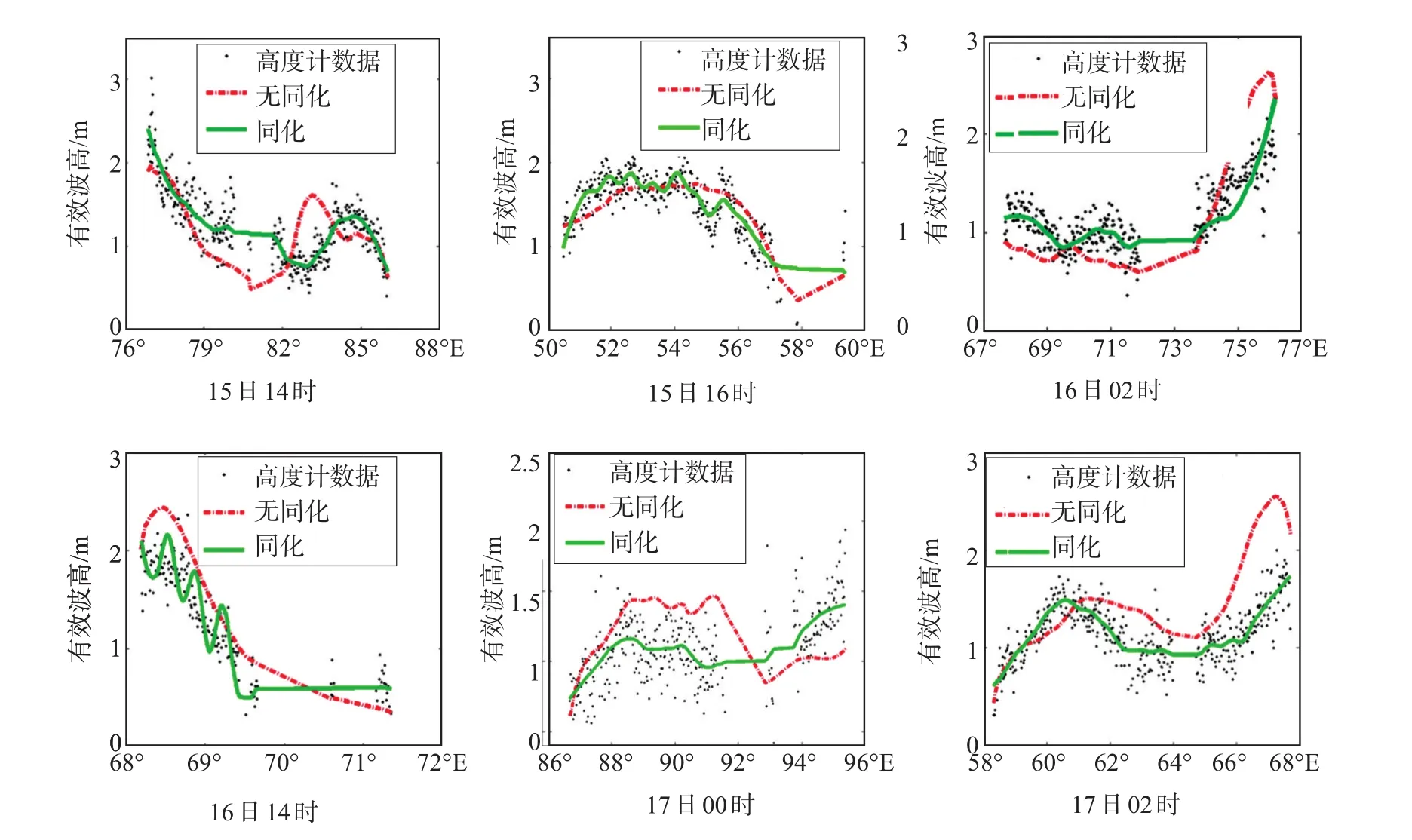
圖3 不同時刻同化的和無同化的模式結果（SWH）與高度計測量（SWH）的比較

為定量評估同化改善模式預報初始場的效果，引入以下統計量，

均方根誤差：

相關系數：

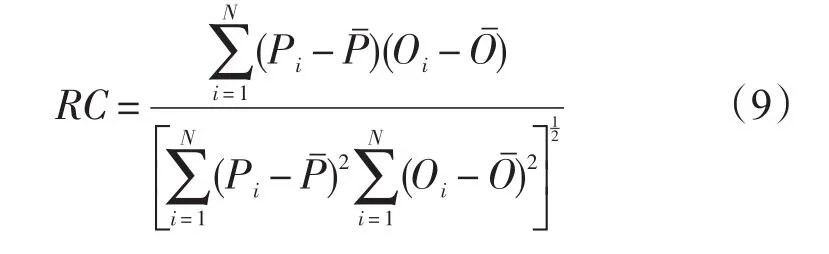
式中，Pi代表模式輸出值，Oi代表觀測值，N為樣本個數。

為簡單起見，我們將15日、16日和17日各日在觀測時刻（見表1）的數據（包括同化和無同化的模式輸出SWH及高度計SWH）按所在的日期分別并入一個統計組，進行統計特征量的計算，計算結果列于表2。由表2容易看出，同化模式輸出的SWH與高度計SWH之間的均方根誤差較無同化的情況明顯地減小，而相關系數明顯地增大。這表明，高度計SWH數據同化模式的初始場與觀測更為接近，表明所研制的高度計波高數據同化模塊是有效的，能夠起到改善模式分析場的作用。

4 同化初始場影響預報結果的時效性

海浪模式預報對于時間跨度太長的初始場是不敏感的。為考察同化初始場影響短期海浪預報結果的時效性，取軌道上數據連續，數據較多的同化時刻，且其后不能再有與其相交或離它很近的同化軌道，以免影響到檢測效果。我們選擇2010年12月17日14時，以同化和無同化所形成的初始場（見圖4中17日14時的同化初始場與高度計SWH的沿軌分布更接近）為起點，對其后6 h、12 h、24 h、36 h、48 h、60 h和72 h等各預報時間點上輸出的預報結果進行比較（見圖4），其中，還將6 h前（即17日14時）的沿軌高度計SWH拿來與6 h預報的同化預報結果和無同化的預報結果進行比較，以考察它們何者更接近于觀測。

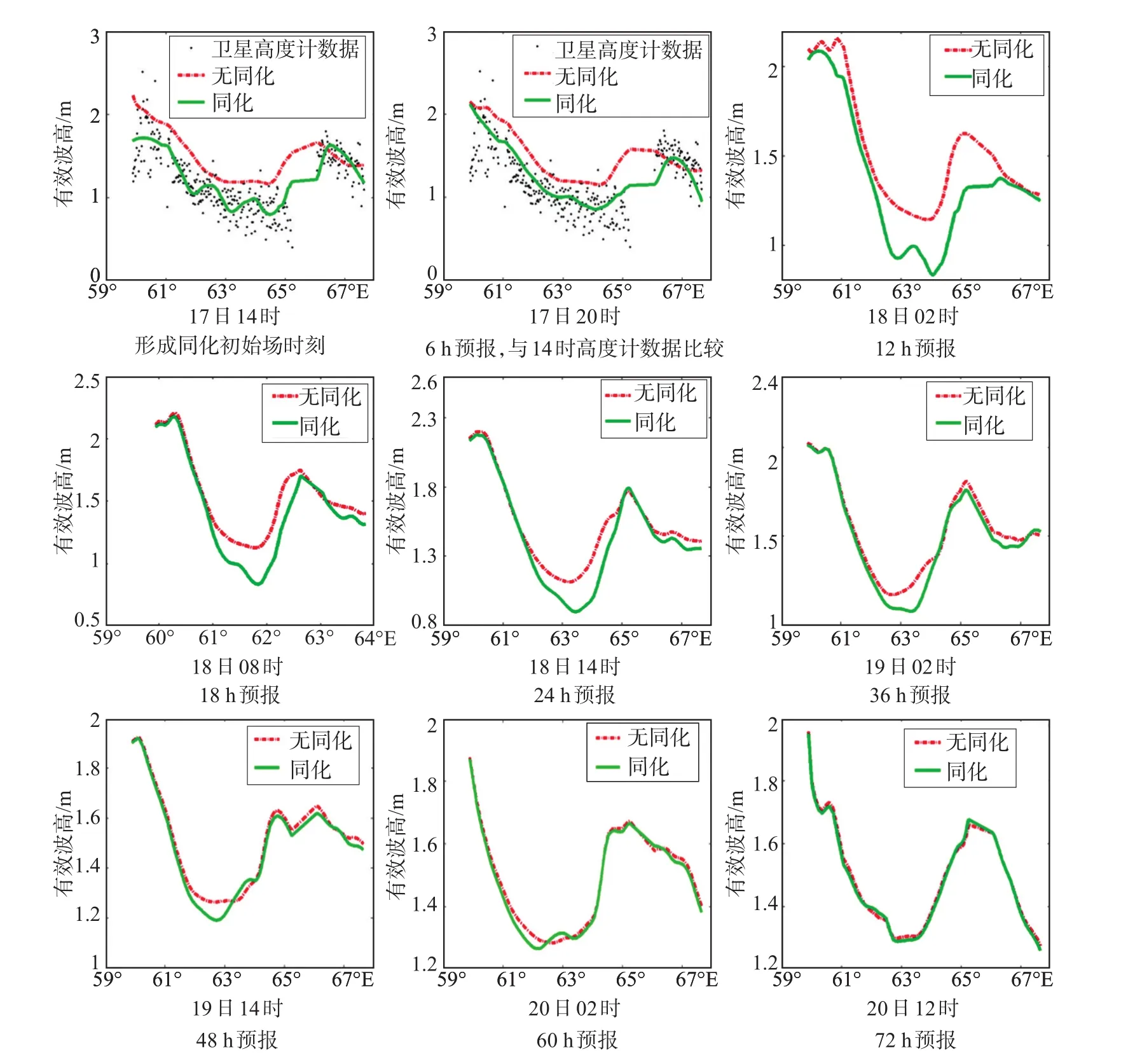
圖4 同化初始場對預報影響時效性的試驗結果

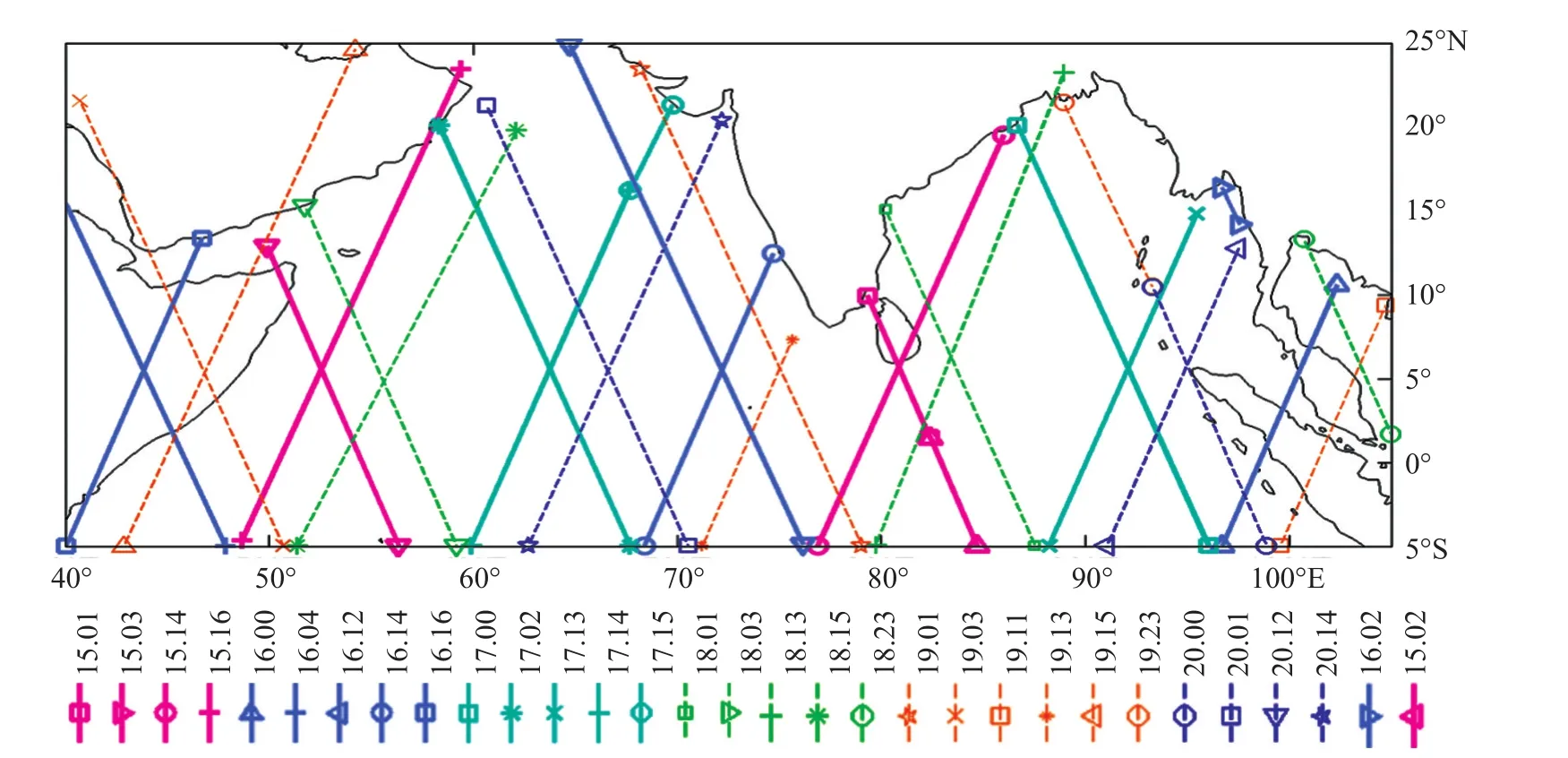
圖5 Jason-2衛星軌道（2010年12月15日00時—20日23時時間段）

表3 預報階段高度計波高數據所在時刻

顯然，對于6 h預報（即17日20時），同化初始場的6 h預報結果較無同化的預報結果更接近6 h前的高度計觀測。隨著預報時段延長，對后期預報結果的影響，同化模式與無同化模式之間趨于減小；從60 h以后的預報結果來看，同化預報和無同化預報之間差別基本消失。另外，從這一組圖來看，無同化的模式預報結果普遍偏大，特別是在波高較小區域。

5 高度計SWH同化對北印度洋海域海浪預報影響評估

為評估高度計SWH數據同化初始場對印度洋海域海浪預報影響，我們以連續同化12月15日、16日和17日3天的該海域高度計SWH數據得到的同化分析場作為預報初始場，進行12月18日、19日和20日3天（即從6 h直到72 h）的印度洋海域短期海浪預報。前3天的高度計測量數據被同化到預報模式，形成同化分析場和預報初始場，后3天（即預報階段）的高度計數據則不再參加同化，而是用于對預報結果的檢驗評估。上述6天（即12月15—20日）有衛星觀測值的時刻詳見表1和表3。

圖5粗實線表示用于同化的高度計數據的衛星軌道位置，細虛線表示用來作檢驗的數據的軌道位置。該圖下方是各條軌道所對應的具體時刻，如15.01表示15日01時刻。這些軌道分別就是2010年12月15日、16日、17日、18日、19日和20日各日各時刻（以此時刻為中心，并在其±0.5 h時間范圍內取觀測數據）經過該目標區域的軌道。由于Jason-2衛星在這6天之內在該區域沒有重復的軌道，一天之內又分為下行線和上行線，所以同化之后，在同一個同化位置沒有新的高度計觀測數據可用來檢測同化后的預報效果，因而檢驗預報效果只能利用其附近的軌道上的觀測數據。相鄰的用來同化和用來檢驗的軌道如果同為上行線或下行線則它們是相互平行的；如果一根為上行線而另一根為下行線則它們是相交的；但是，它們之間的時間差卻都不小。舉例來說，2010年12月18日01時刻的軌道是下行線，而與其（在時間上）最近的下行線是15日01時刻和15日02時刻的，與其相交的上行線是15日14時刻的，故它們之間時間上相距都已超過72 h。由此，在同化時刻過去72 h之后再來檢驗同化對預報影響的效果其實是很困難的。因為，模式經過1 h一次的風場驅動，3天以后的同化與無同化的風浪場結果之間基本就沒有什么差別了。另外，由于我們在該目標區域目前還難以獲得浮標等其它來源的觀測數據，所以，為檢驗同化預報的效果也只有利用高度計測量數據了。故在文中還是給出了同化預報和無同化預報在有高度計觀測時刻的SWH比較圖，但因為用于同化的與用于檢驗的二者時間上相距太長，同化雖有優勢但已不明顯。圖6中，每幅圖下方括號中所標注的是與該驗證時刻較近的用來同化的觀測數據其軌道所對應的時刻。可以看出，它們在時間間隔上都很長，都超過了48 h，有的還超過了72 h。但從這組圖中還是可以看出加入同化的預報要比無同化的效果好，不過隨著積分時間的延長，同化與無同化效果漸趨一致。

6 結論與展望

海浪的模式預報對于時間跨度太長的初始場并不敏感，而大氣模式提供的即時風場又總是存在著一定的誤差。因此，為提高海浪模式預報精度，及時更新和提高海浪模式預報初始場的質量是解決途徑之一，即在海浪模式的積分運算過程中應充分利用當前衛星遙感技術所能提供的觀測數據，盡可能大面積吸收高度計測量海浪數據并利用一定的同化手段及時更新海浪分析譜，如此可為模式預報提供更接近準確的初始場，從而提高海浪模式預報的精度。

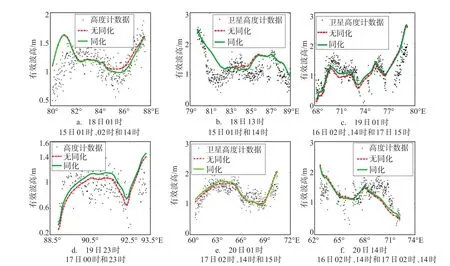
圖6 預報階段同化、無同化預報結果比較（包括與最近的高度計觀測的比較）

研制了基于OI方法的高度計波高數據同化并行模塊，并將其植入WAVEWATCH IIITM，使同化模式仍能保證其以并行方式運行。為解決同化背景場誤差協方差矩陣占用內存較大問題，采用稀疏矩陣的存儲方法節省內存和使用Sparse Blas函數庫中的相關函數，使該問題得到較好解決。

以5°S以北的印度洋海域作為目標計算區域，嵌套在WAVEWATCH IIITM的全球網格中，較好解決了目標區域的開邊界條件問題。所建立的海浪同化預報模式由大氣模式WRF輸出的一小時一次的海面10m風場驅動運行。同化模式的結果（SWH）和無同化的模式結果（SWH）分別與高度計測量波高（SWH）比較，顯示高度計波高數據同化可明顯改善模式預報初始場。

進行印度洋目標區域海浪場72 h以上時段同化預報試驗，初步分析表明，同化高度計SWH數據進入海浪模式進行邊同化邊預報，能起到改善海浪短期預報效果的作用；但同化影響模式預報的時效性，限于72 h內；預報時效越短，同化模式的結果與無同化的模式結果之間差別越顯著。

總之，本文初步研究表明，連續同化高度計SWH數據進行邊同化邊預報可望明顯提高海浪短期預報結果的精度。

在強調高度計波高數據同化改善海浪模式預報水平的同時，我們也注意到，由于衛星觀測所獲得的僅是星下點數據，因此，其軌道重現頻率與空間覆蓋率一直如同一對矛盾。若要追求空間上的高覆蓋率，則其軌道重現頻率必然受到影響。例如，Envisat衛星兩相鄰軌道之間最寬距離僅80 km，但其軌道完全重合一次的周期卻需35天之久；Jason-2，Jason-1的完全重合周期為10天，但兩相鄰軌道間的距離卻寬達315 km。總之，在本文的研究中不難發現，僅依靠單衛星提供的波高數據是相當有限的，而且無法做到時空同步（實時提供大范圍海浪場的高度計測波資料），難以滿足進行大洋區域海浪場同化預報時對大面積吸收實測海浪資料的渴求。因而，今后應考慮利用多衛星融合的高度計波高資料進行大洋海浪場的同化預報，應能至少在一定程度上彌補上述不足。例如，利用最近的短時段可獲得的Cryosat-2，Jason-2，Jason-1以及Envisat等4顆衛星（隨著新衛星上天，將不斷有新的衛星高度計資料作為數據源加入）在內的最少兩顆衛星的數據，通過一定的濾波方法進行空間平滑和外插處理之后，得到準實時的多衛星融合的測波資料用于大范圍海浪場的同化預報。

[1]Esteva D C.Evaluation of preliminary experiments assimilating Sea sat significant wave heights into a spectral wave model[J].J GeophysRes,1988,93(C11):14099-14105.

[2]Janssen PA E M,Lionello P,Reistad M,et al.Hind cast and data assimilation studies with the WAM model during the Sea sat period[J].J Geophys Res,1989,94:973-993.

[3]Lionello P, GüNTHER H, Janssen PAE M.Assimilation of altimeterdata in a global third-generation wave model[J]. J Geophys Res,1992, 97(C9): 14453-14474.

[4]Mastenbroek C,Makin V K,Voorrips A C,et al.Validation of ERS-1 altimeter wave height measurements and assimilation in a North Sea wave model[J].Global Atmos Ocean Syst,1994,2:143-161.

[5]Breivik L A,Reistad M.Assimilation of ERS-1 altimeter wave heights in an operational numerical wave model[J].Weather Fore-cast,1994,9:440-451.

[6]Lionello P,Guenther H,Hansen B.ASequential data Assimilation Scheme Applied to the Global Wave Analysis and Prediction[J].J MarSyst,1995,6:87-107.

[7]Bender LC,GlowackiT.The assimilation of altimeter data into the Australian wave model[J].Aust Meteorol Mag,1996,45:41-48.

[8]Greensladed J M.The assimilation of ERS-2 significant wave height data in the Australian region[J].J Mar Syst,2001,28:141-160.

[9]張志旭,齊義泉,施平，等.衛星高度計波高資料的同化實驗分析[J].海洋學報,2003,25(5):21-28.

[10]王毅,余宙文.衛星高度計波高數據同化對西北太平洋海浪數值預報的影響評估[J].海洋學報,2009,31(6):1-6.

[11]EliassenA.Provisional report on calculation of spatial covariance and autocorrelation of the pressure field[R].Institute for Weather andClimateResearch,AcadSci,Oslo,ReportNo.5,1954.