兩兩可換的對合矩陣的群逆和可逆性

李虹曄, 崔小琴

(湖北師范學院 數學與統計學院， 湖北 黃石 435002)

1 引言及預備引理

冪等矩陣和對合矩陣是矩陣分析和算子理論中,兩類最基本的矩陣,它們在矩陣分析、算子理論、統計學、經濟學等中起著很重要的作用.在[1]中Graybill F A發現了兩個冪等矩陣的線性組合在統計學中的作用.人們對于這兩類矩陣組合的問題有不少的研究成果.例如:秩、可逆性、群逆、Drain逆等.在[2]和[3]中,Tian研究了兩個冪等陣的線性組合及塊為冪等陣的組合的分塊矩陣的秩.在[4-7]中,Zuo和Gro J ,Trenkle G,以及Koliha J J,Rakocevic V研究了兩個冪等矩陣的線性組合可逆性.在[8-11]中Deng和Zhang研究了冪等矩陣的和與差的Drain逆.本文先研究了兩個冪等(對合)矩陣之差的可逆性和群逆的充要條件，并給出了三個兩兩可換的對合矩陣組合的群逆和可逆性的幾個充要條件.

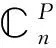
設P∈n×n,令,則P∈?A=I-2P∈,從而A∈?∈

設A∈n×n,如果存在唯一的X∈n×n使得AXA=A,XAX=X,AX=XA成立.則稱A是一個群逆陣,且X是A的 群逆.用A#來表示A的群逆.容易證明,若A的群逆存在,則群逆一定唯一.且A是群逆陣?r(A)=r(A2) .用表示所有的n階群逆陣組成的集合,即:

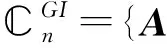
由文獻[12]，我們有

引理1 設P是冪等矩陣,則存在n階可逆陣S,使得

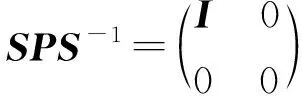
a)M#存在?A#與C#都存在,并且AπBCπ=0 .其中Aπ=I-AA#,Cπ=I-CC#.

b)如果M#存在,則

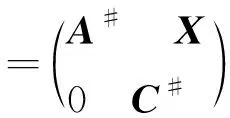
其中X=(A#)2BCπ+BCπ+AπB(C#)2-A#BC#.

2 主要結果及其證明

定理1 若P,Q是兩個冪等矩陣,則有

1)P-Q可逆當且僅當I-PQ和P+Q-PQ可逆.

2)P-Q是群逆陣,則I-PQ和P+Q-PQ是群逆陣.

證明1):? 設P-Q可逆，則(P-Q)2是可逆的. ?x∈N(I-PQ),有

x=Px=PQx,QPx=QPPQx=QPQx=Qx,(P-Q)2x=(P+Q-PQ-QP)x=0

可得出x=0 .從而I-PQ是可逆的.

又因為?x∈N(P+Q-PQ), 則有Px+(Q-PQ)x=0.兩邊同乘P,可得出Px=0,有

(Q-PQ)x=0=(Q2-PQ)x=(Q-P)Qx=0

又因為P-Q可逆,則

Qx=0,Px=Qx=0=(P-Q)x=0

P-Q可逆,則x=0.從而P+Q-PQ是可逆的.

? 設I-PQ與P+Q-PQ都可逆,對?x∈N(P-Q) ,則有

Px=Qx=PQx=QPx,PQPQx=PQPx

而

(I-PQ)(P+Q-PQ)x=(P+Q-PQ-PQP-PQ+PQPQ)x=

Px+Qx-2PQx-PQPx+PQPQx=0

因為I-PQ與P+Q-PQ都可逆,有x=0.從而P-Q可逆.

2)P-Q是群逆陣,由引理1，設

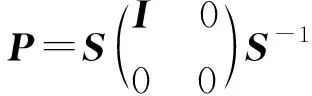
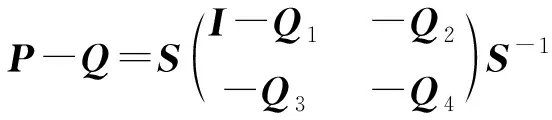
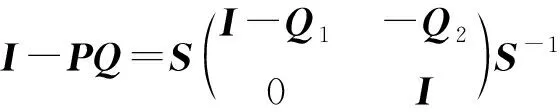
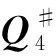
定理2 設A,B是兩個對合矩陣，有

1)A-B可逆當且僅當3I+A+B-AB, 3I-A-B-AB可逆.

2)A-B是群逆陣,則3I+A+B-AB,3I-A-B-AB是群逆陣.

證明 設

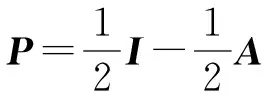
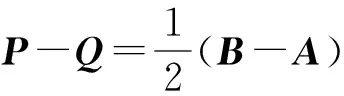
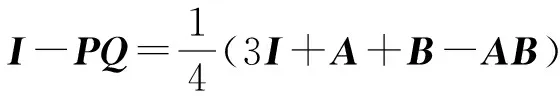
由定理1,我們得到A-B可逆，當且僅當 3I+A+B-AB和 3I-A-B-AB都可逆.同時由A-B是群逆陣，則3I+A+B-AB和3I-A-B-AB是群逆陣.

定理3 設A,B,C滿足A2=B2=C2=I,且A,B,C兩兩可換

T=aI+bA+cB+dC+eAB+fBC+gAC+hABC

則有

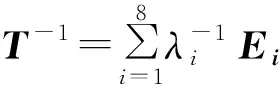
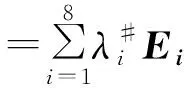
其中Ei和λi，i=1,2,…,8 定義如下:

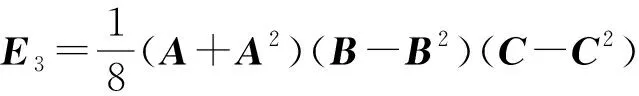
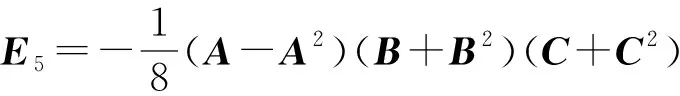
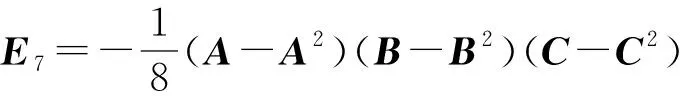
λ1=a+b+c+d+e+f+g+h,λ2=a+b+c-d+e-f-g-h

λ3=a+b-c-d-e+f-g+h,λ4=a+b-c+d-e-f+g-h

λ5=a-b+c+d-e+f-g-h,λ6=a-b+c-d-e-f+g+h

λ7=a-b-c-d+e+f+g-h,λ8=a-b-c+d+e-f-g+h

證明 由于A,B,C可對角化且它們兩兩可換,所以我們可以對A,B,C作如下的分解

A=S(I⊕I⊕I⊕I⊕-I⊕-I⊕-I⊕-I)S-1

B=S(I⊕I⊕-I⊕-I⊕I⊕I⊕-I⊕-I)S-1

C=S(I⊕-I⊕-I⊕I⊕I⊕-I⊕-I⊕I)S-1

那么可分別計算

A+A2=S(2I⊕2I⊕2I⊕2I⊕0⊕0⊕0⊕0)S-1

B+B2=S(2I⊕2I⊕0⊕0⊕2I⊕2I⊕0⊕0)S-1

C+C2=S(2I⊕0⊕0⊕2I⊕2I⊕0⊕0⊕2I)S-1

A-A2=S(0⊕0⊕0⊕0⊕-2I⊕-2I⊕-2I⊕-2I)S-1

B-B2=S(0⊕0⊕-2I⊕-2I⊕0⊕0⊕-2I⊕-2I)S-1

C-C2=S(0⊕-2I⊕0⊕-2I⊕0⊕-2I⊕0⊕-2I)S-1

從上面的表達式中,觀察可得

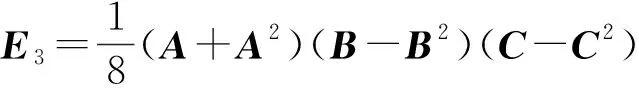
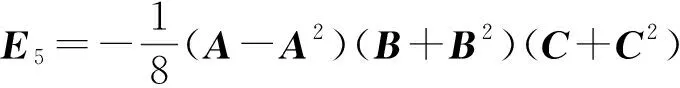
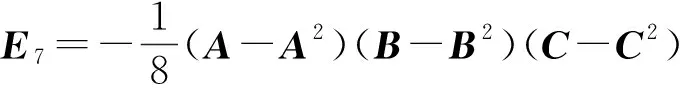
又因為

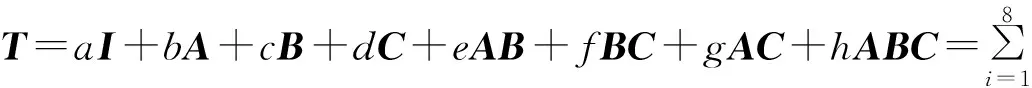
則可得

λ1=a+b+c+d+e+f+g+h,λ2=a+b+c-d+e-f-g-h

λ3=a+b-c-d-e+f-g+h,λ4=a+b-c+d-e-f+g-h

λ5=a-b+c+d-e+f-g-h,λ6=a-b+c-d-e-f+g+h

λ7=a-b-c-d+e+f+g-h,λ8=a-b-c+d+e-f-g+h

我們知道

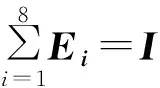
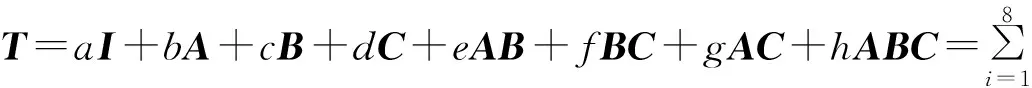
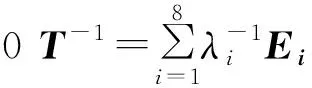
參考文獻：

[1]Fraybill FA.Introduction to matrices with applications in statistics[M].wadsworth publishing compang Inc.california,1969.

[2]Tian Yongge, Styan G P H.Rank equlities for idempotent and involutory matries[J]. Linear Algebra Appl,2001,335:101～117.

[3]Tian Yongge,Styan G P H.Rank equlitiesfor idempotent matries with applications[J].Journal of Computational and Applied Math, 2006,191:77～97.

[4]Zuo Kezheng.Nonsingularity of the difference and the sum of two idempotent matrices[J].Linear Algebra Appl,2010,433:476～482.

[5]Gro J,Trenkler G.Nonsingularity of the difference oftwo oblique projectors[J]. SIAM J Matrix Anal Appl,1999,21:390～395.

[6]Koliha J J, Rakocevic V.Invertibility of the difference of idempotents[J].Linear and Multilinear Algebra, 2003,51:97～110.

[7]Koliha J J, Rakocevic V, Straskraba I.The difference and sum of projectors[J]. Linear Algebra Appl,2004,388:279～288.

[8]Deng Chunyuan.The Drain inverses of products and difference of orthogonal projections[J].J Math Anal Appl,2007,335:64～71.

[9]Zhang S, Wu J.The Drain inverse of the linear combinations of two idempotents in the Banach algebra[J]．Linear Algebra Appl.2012,436:3132～3138.

[10]Deng Chunyuan.The Drain inverses of sum and difference of idempotents[J].Linear Algebra Appl,2009,430:1282～1291.

[11]Deng Chunyuan.Characterizations and representations of the group inverse involving idempotents[J]．Linear Algebra Appl,2011,434:1067～1079.

[12]Horn R A ,Johnson C R.矩陣分析[M]. 北京:人民郵電出版社，2005.

[13]Julio Benitez,Murat Sarduvan,Sedat Ulker,et al.On nonsingularity of combinations of three group invertible matrices and three tripotent [J].Linear Algebra Appl,2013,61:463～481.

[14]孫文瑜,何旭初.矩陣引論[M]. 南京:江蘇科學技術出版社,1990.