錐度量空間中一類壓縮映射不動點定理

江秉華

(湖北師范學院 數學與統計學院， 湖北 黃石 435002)

1 預備知識

眾所周知, 非線性映射的不動點的存在唯一性是非線性分析的重要課題之一, 而且不動點理論廣泛地應用于非線性積分方程和微分方程中.文[3]通過引入Banach 空間代替實數集合, 引進了錐度量空間并且證明了完備錐度量空間中Banach 壓縮映象原理仍然成立. 此后, 壓縮不動點定理在錐度量空間中得到推廣和應用.受文[1～2]啟發, 本文證明了錐度量空間中一類壓縮不動點定理, 推廣了相關文獻結果.

下面先介紹一些基本概念和已知結果.

設E是實Banach 空間，P是E的一個子集, 如果

1)P是非空閉集且P≠{θ} ;

2)?a,b∈+,x,y∈P,則ax+by∈P；

3) 若x∈P,-x∈P, 則x=θ;

則稱P是一個錐. 規定x≤y?y-x∈P,熟知“ ≤”是E上一個偏序，稱“ ≤”為P誘導的偏序關系. 用x0，使得當θ≤x≤y時，‖x‖ ≤K‖y‖ (x,y∈E), 則錐P稱為正規錐. 滿足上式的最小正常數K稱為P的正規常數. 如果intP≠?，則稱錐P是體錐.

在本文中，總假設E為實Banach 空間, 錐P?E是體錐， “ ≤ ”為P誘導的一個偏序關系.

定義1 設X是一個非空集合，映射d：X×X→E滿足

d1)θ≤d(x,y),?x,y∈X;d(x,y)=θ?x=y;

d2)d(x,y)=d(y,x),?x,y∈X;

d3)d(x,y)≤d(x,z)+d(y,z),?x,y,z∈X;

則稱d為X上的一個錐度量，同時稱 (X,d)為錐度量空間.

錐度量空間是向量度量空間的推廣.

定義2 設(X,d) 為錐度量空間，

1) 若?c?θ, 存在正整數N，使得當n,m>N時，有d(xn,xm)?c, 則稱{xn} 為柯西列；

2) 若?c?θ,存在正整數N，使得當n>N時，有d(xn,x)?c, 則稱{xn} 收斂于x∈X；

3) 若X中任意Cauchy列都是收斂序列，則稱X是完備的錐度量空間.

2 主要結果

在這里省略了[1]中錐的正規性這個條件，給出定義在錐度量空間中映射公共不動點定理.

定理1 設(X,d) 是一個完備的錐度量空間，P是E中的一個錐，假設映射f,g:X→X滿足

d(fx,gy)≤λ1d(x,y)+λ2d(x,fx)+λ3d(y,gy)+λ4[d(x,gy)+d(y,fx)]

(1)

對?x,y∈X都成立，其中λi≥0 為常數，i=1,2,3,4,λ1+λ2+λ3+2λ4< 1，則f和g在X中有唯一的公共點不動點.

證明 取x0∈X設x2n+1=fx2n,x2n+2=gx2n+1(n=0,1,2,3…),則得到一個序列{xn} . 因此，由(1)式，對于正整數n，有

d(x2n+1,x2n+2)=d(fx2n,gx2n+1)≤

λ1d(x2n,x2n+1)+λ2d(x2n,fx2n)+λ3d(x2n+1,gx2n+1)+λ4[d(x2n,gx2n+1)+d(x2n+1,fx2n)]=

λ1d(x2n,x2n+1)+λ2d(x2n,x2n+1)+λ3d(x2n+1,x2n+2)+λ4[d(x2n,x2n+2)+d(x2n+1,x2n+1)]=

(λ1+λ2+λ4)d(x2n,x2n+1)+(λ3+λ4)d(x2n+1,x2n+2)

所以

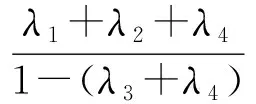
類似地，有

d(x2n+2,x2n+3)≤δ·d(x2n+1,x2n+2)

綜上，對任意正整數n，有

d(xn+1,xn+2)≤δd(xn,xn+1)≤…≤δn+1d(x0,x1)

故對正整數m和n，當m>n時，有

d(xm,xn)≤d(xn,xn+1)+d(xn+1,xn+2)+…+d(xm-1,gxm)≤

(δn+δn+1+…+δm-1)d(x1,x0)≤

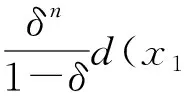
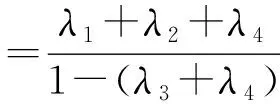
現在由(1)式，得到

d(p,gp)≤d(p,x2n+1)+d(x2n+1,gp)=d(p,x2n+1)+d(fx2n,gp)=

d(p,x2n+1)+λ1d(x2n,p)+λ2d(x2n,x2n+1)+λ3d(p,gp)+λ4[d(x2n,gp)+d(p,x2n+1)]≤

d(p,x2n+1)+λ1d(x2n,p)+λ2d(x2n,x2n+1)+λ3d(p,gp)+λ4[d(x2n,p)+d(p,gp)+d(p,x2n+1)]

并且

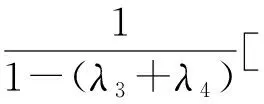
設θ?c, 選取一個正整數N2，當n>N2時有

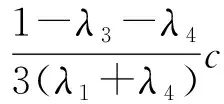
然后d(p,gp)?c，由于c的任意性，故d(p,gp)=θ?p=gp注意到

d(p,fp)=d(gp,fp)≤λ1d(p,p)+λ2d(p,fp)+λ3d(p,gp)+λ4[d(p,gp)+d(p,fp)]=

(λ2+λ4)d(p,fp)

有(1-λ3-λ4)·d(p,fp)≤θ, 又 0≤λ1+λ2+λ3+2λ4<1?(1-λ3-λ4)>0,所以d(p,fp)=θ, 即fp=p=gp

綜上，得到f和g有公共不動點p. 下面證明它們的公共不動點是唯一的.

假設存在另一個點q∈X使得fq=gq=q，因此由(1)式，有

d(p,q)=d(fp,gq) ≤

λ1d(p,q)+λ2d(p,fp)+λ3d(q,gq)+λ4[d(p,gq)+d(q,fp)]=

(λ1+2λ4)d(p,q)

又因為0≤λ1+λ2+λ3+2λ4<1 ，有0≤λ1+2λ4<1 ， 所以d(p,q)=θ，即p=q.因此f和g有唯一的公共不動點.

推論1 設(X,d) ， 是一個完備的錐度量空間，λi≥0 (i=1,2,3,4) ,且λ1+λ2+λ3+2λ4<1.p,q為兩個自然數. 若映射f:X→X滿足對?x,y∈X, 有

d(fpx,fqy)≤λ1d(x,y)+λ2d(x,fpx)+λ3d(y,fqy)+λ4[d(x,fqy)+d(y,fpx)]

(2)

則f存在唯一的不動點.

證明 將fp,fq分別看作定理1中f,g，再利用不動點的唯一性可證得命題.

推論2 設(X,d) 是一個完備的錐度量空間，若映射f:X→X滿足對?x,y∈X, 有

d(fx,fy)≤λ1d(x,y)+λ2d(x,fx)+λ3d(y,fy)+λ4[d(x,fy)+d(y,fx)]

(3)

其中λi≥0(i=1,2,3,4)，λ1+λ2+λ3+2λ4<1,則f存在唯一的不動點.

證明 在推論1中令p=q=1，結合其證明過程，即得結論.

推論3 設(X,d) 是一個完備的錐度量空間，若映射f:X→X滿足

d(fx,fy)≤λd(x,y),?x,y∈X

(4)

其中0≤λ<1, 則f存在唯一的不動點.

推論4 設(X,d) 是一個完備的錐度量空間，若映射f:X→X滿足

d(fx,fy)≤λ1d(x,fy)+λ2d(y,fx),?x,y∈X

(5)

其中λ1,λ1∈[0,1/2), 則f存在唯一的不動點.

推論5 設(X,d) 是一個完備的錐度量空間，若映射f:X→X滿足

d(fx,fy)≤λ1d(x,fy)+λ2d(y,fx),?x,y∈X

(6)

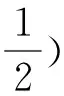
上面的引理是[3]中定理4的推廣.

推論6 設(X,d) 是一個完備的錐度量空間，若映射f:X→X滿足

d(fx,fy)≤λ1d(x,y)+λ2d(x,fx)+λ3d(y,fy)

(7)

對 ?x,y∈X都成立，其中λi≥0(i=1,2,3) ，λ1+λ2+λ3<1,則f在X中存在唯一的不動點.

一個顯而易見的事實：如果一個映射f有一個不動點p，那么對任意的自然數n,p也是映射fn的不動點. 但反過來不成立. 如果滿足F(f)=F(fn) ，(這里F(f) 表示映射f的所有不動點的集合)，則稱此映射滿足性質P(見文獻[4]). 如果F(f)∩F(g)=F(fn)∩f(gn)，那么稱f和g具有性質Q.

定理2 設(X,d) 是一個錐度量空間，映射f:X→X滿足

d(fx,f2y)≤λd(x,fy),?x,y∈X

(8)

如果① 0≤λ<1，或者 ② 當λ=1 時， ?x∈X,x≠fx

d(fx,f2y)

若F(f)≠? ，則f滿足性質P.

證明 因為n=1 時顯然成立，我們總是假設n>1 . 取u∈F(fn) ，若f滿足條件①，那么

d(u,fu)=d(f(fn-1u),f2(fn-1u))≤λd(fn-1u,fnu)≤λ2d(fn-2u,fn-1u)≤ …≤λnd(u,fu)

所以d(u,fu)=0, 進而有u=fu. 若f滿足條件②，則fu=u顯然成立. 若不然u≠fu，重復①的證明，就會導致d(u,fu)

定理3 設(X,d) 是一個完備的錐度量空間，若映射f，g:X→X滿足(1)式，則f,g具有性質Q.

證明 由定理1知，f,g在X中有唯一公共不動點，設u∈F(fn)∩F(gn)，則

d(u,gu)=d(f(fn-1u),g(gnu))≤λ1d(fn-1u,fnu)+λ2d(fn-1u,fnu)+λ3d(fnu,gn+1u)+

λ4[d(fn-1u,gn+1u)+d(fnu,gnu)]≤

λ1d(fn-1u,u)+λ2d(fn-1u,u)+λ3d(u,gu)+λ4d(fn-1,gu)=

λ1d(fn-1u,u)+λ2d(fn-1u,u)+λ3d(u,gu)+λ4d(fn-1u,u)+λ4d(u,gu)=

(λ3+λ4)d(u,gu)+(λ1+λ2+λ4)d(fn-1u,u)

從而

進而

d(u,gu)=d(fnu),gn+1u))≤δd(fn-1u,u)≤…≤δnd(fu,u)

故F(fn)∩F(gn)?F(f)∩F(g), 故f,g具有性質Q.

參考文獻：

[1]Abbas M, Rhoades B E.Fixed and periodic point results in cone metric space[J]. Applied Mahgematics Letters,2009,22:511～515.

[2]Abbas M, Jungck G.Common fixed point results for noncommuting mappings without continuity in cone metric space[J]. J Math Anal Appl,2008,341:416～420.

[3]Huang Long-Guang, Xian Zhang.Cone metric space and fixed point theorems of contractive mappings[J]. J Math Anal Appl,2007,332:1468～1476.

[4]Rezapour Sh, Hamlbarani R.Some notes on the paper "Cone metric spaces and fixed point gheorems of contractive mappings"[J]. J Math Anal Appl,2008,345:719～724.

[5]Jeong G S, Rhoades B E.Maps for which F(f)=F(fn)[J].Fixed point Theory Appl,2005,6:87～131.