四旋翼飛行器PID優化控制

王史春

(1.臺州職業技術學院，浙江臺州 318000；2.浙江大學智能系統與控制研究所，工業控制技術國家重點實驗室,浙江杭州 310027)

四旋翼飛行器是一個具有六自由度和4個控制輸入的非線性欠驅動系統，具有對外界和自身抗干擾敏感的特性，控制的主要問題是解決強耦合性和不穩定的動力特性。姿態控制是整個飛行控制的關鍵，如果能精確控制飛行器姿態，模型相對還是比較明確的，難度仍然在PID參數的整定上[1]，其參數調整很大程度上依賴于設計人員自身經驗，只能人為的多次調試才能確定，達到穩定狀態，但不一定是最佳參數。針對本實驗室在設計時遇到的以上問題，提出了改進的PSO算法[2]和遺傳算法相結合方法來優化PID參數。四旋翼飛行器是多變量系統，需多目標搜索，PSO算法全局搜索能力強，算法實現簡單，能夠實現多個目標尋優，尋找合適的參數，以達到理想的效果。遺傳算法在不需要給出控制器初始參數的情況下，通過復制、交叉、變異操作，尋找到合適的參數，達到尋優，使控制目標滿足要求，同時能解決多值函數問題以及在多參數尋優中，容易造成尋優失敗或時間過長的問題，具有局部搜索能力強的特點，并能從多點開始并行操作，高效啟發式搜索，避免了過早陷入局部最優解[3]。

1 動力性建模

四旋翼飛行器是一個非線性、多變量、高度耦合的欠驅動系統[4]。為實現對四旋翼飛行器這一欠驅動系統的有效控制，必須準確建立其在各種飛行狀態下的數學模型。為了得到四旋翼飛行器的數學模型，先建立2個基本坐標系：如圖1所示，地面坐標系G(OXYZ)和機體坐標系S(oxyz)。在飛行器飛行過程中，地面坐標系保持不變。如圖2所示，地面坐標系G與機體坐標系S的定位關系分別用歐拉角表示，分別為俯仰角φ，翻滾角θ，偏航角ψ。兩坐標系的旋轉關系通過旋轉矩陣表示為

(1)

(2)

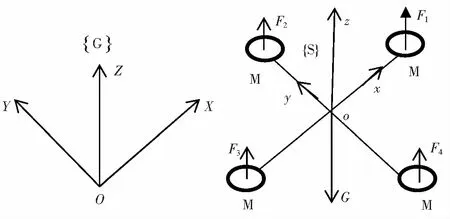
圖1 四旋翼飛行器示意圖Fig.1 Schematic diagram of quadrotor

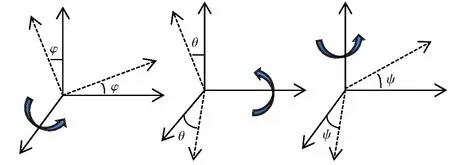
圖2 歐拉角Fig.2 Euler angle

為了簡化四旋翼飛行器的動力學模型[4]，根據牛頓第二定律[5]，飛行器動力學方程表示為

(3)

(4)

式中：F為飛行器所加外力和；m為飛機質量；v為飛行器速度；M為飛行器所有外力距[6]的和；H為飛行器相對于地面坐標系絕對動量距。

根據動力學方程，假設Fx，Fy，Fz為F在飛行器坐標系3個坐標軸上的分量;p，q，r為角速度ω在飛行器坐標系3個軸的分量。根據式(1)，式(3)，式(4)得到機體坐標系下線運動方程(Ki為綜合阻力系數)：

(5)

(6)

(7)

本研究是用慣性測量單元測量四旋翼旋轉[7]，而歐拉角是時域變化的連續函數，三軸轉動角速度，通過矩陣表示為

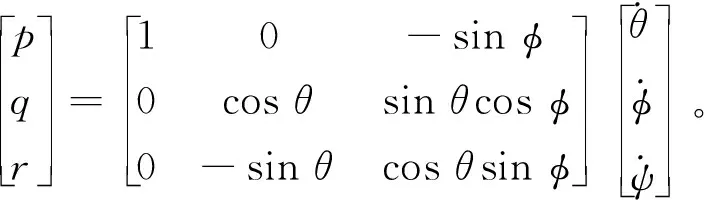
(8)

經拉格朗日推導式(8)可得運動方程表示為

(9)

由式(9)可推出:

(10)

2 遺傳算法優化PID控制器參數

2.1 PID控制

為了把四旋翼飛行器非線性耦合模型分解為4個獨立的控制通道[8]，經過實驗，利用小擾動原理得到的線性方程組用來分析飛行器操縱性、穩定性、有效性，能得到較好效果和好的準確度。在小擾動下進行線性化處理，可得到飛行器小擾動運動，其中，狀態變量：

x=[uvwpqrθφψ]T，

(11)

控制變量：

u=[u1u2u3u4]T。

(12)

為了簡化控制系統的設計，假設姿態角和角速度之間為簡單的積分關系，即

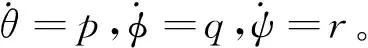
(13)

根據實驗室的四旋翼飛行器有關參數和環境數據以及系統的傳遞函數G(S)=(s×I-A)-1B和線運動方程(5)、方程(6)、方程(7),可得各控制通道的傳遞函數。

俯仰通道：

(14)

翻滾通道：

(15)

偏航角：

(16)

X軸與俯仰角：

(17)

Z軸:

(18)

Y軸與翻滾角：

(19)

2.2 GA-PSO算法優化PID參數

為了優化各通道的PID的3個參數，GA-PSO算法的PID控制器以誤差e和誤差變化率ec作為輸入，以滿足不同時刻的e和ec對PID參數整定的要求,如圖3所示。PID控制器的控制算法為

(20)

在文獻[10]中,提出標準的PSO算法：

(21)

(22)

優化PID控制器參數也取得了一定的成效。標準的PSO算法中粒子的移動是以自身的局部最優和全局最優來改變粒子的方向和速度，容易陷入局部最優值，特別對于多峰值函數。

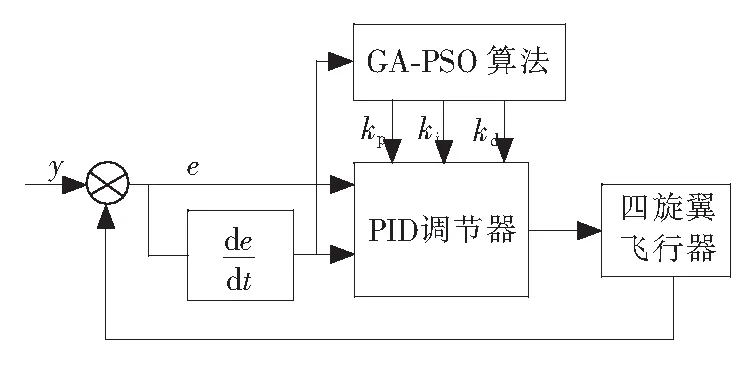
圖3 PID控制器優化結構圖Fig.3 Optimization of PID controller structure

為了更好地對PID參數進行優化控制，提出將改進的PSO算法和遺傳算法結合，其流程如圖4所示，算法的核心思想是通過改進PSO算法，算法如下：

(23)

這里的pm是隨機選取周邊2個粒子，通過比較選取適配值高的粒子位置作為pm的值；Xi(k)和Vi(k)是粒子當前的位置和方向；C是常數，一般取值為2。ω是權重，隨著粒子搜索的進程，值會減少，提高搜索精度。標準的PSO和改進的PSO算法最大不同在于學習過程不一樣，標準PSO算法通過自身最優和局部最優改變自身的速度和位置；而改進的PSO算法通過周邊粒子綜合學習來改變自身的速度和位置，有利于充分學習，達到好的性能。當第一個粒子通過周邊粒子綜合學習后，更新到一個較優的位置，為了避免陷入局部最優，特別對于多峰值函數來說，容易陷入局部最優，通過遺傳算法的選擇、交叉、變異來對粒子進行重新組合，避免了粒子早熟的現象。

本文的算法具有如下創新：

1)PSO和GA結合，發揮各自特長，改善系統的性能，增強算法的適應性；

2)PSO算法的權重系統ω隨搜索進行逐步減小，有利于搜索速度與精度的提高；

3)改進的PSO粒子得到充分學習，遺傳算法又可避免粒子的早熟現象。

圖4中，X1={x11，x12,x13},D是維數,g是代數，max_gen指最大代數pm={pm1,pm2,pm3}。

3 仿真實驗和飛行實踐

本仿真實驗是通過對標準PSO算法和GA-PSO算法進行比較，來驗證算法的優越性。采用時間為1 s,輸入指令為一階躍信號。為獲取滿意的過度過程動態特性，采用誤差絕對值時間積分性能指標作為參數選擇的最小目標函數[9]。為了防止控制能量過大，在目標函數中加入控制輸入的平方項。選用式(24)作為參數選取的最優指標：

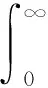
(24)

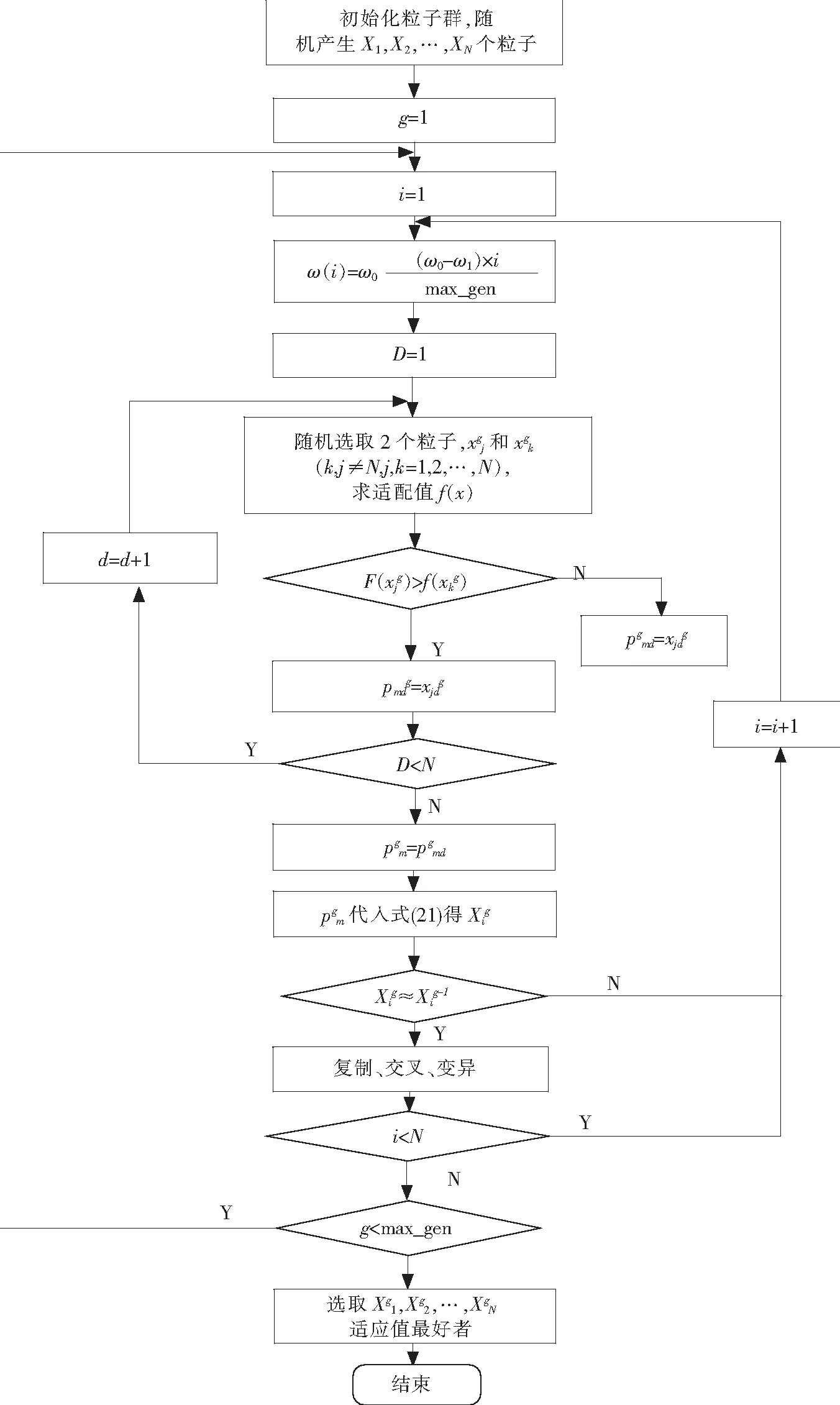
圖4 GA-PSO控制優化流程圖Fig.4 Chart of GA-PSO control and optimization

其中：e(t)為系統誤差;u(t)為控制器輸出;tu為上升時間；ω1,ω2,ω3為權值。

為了避免超調，采用了懲罰函數[10]，即一旦產生超調，將超調量作為最優指標的一項，此時最優指標為

Ife(t)<0,

ω4|e(t)|dt)+ω3×tu。

(25)

PSO算法中粒子數為40，最大代數為100，學習因子為1.51，權重ω代入式(25)計算可得。遺傳算法交叉概率和變異概率分別為pc=0.92,pm=0.035。仿真實驗結果如圖5—圖10所示，標準PSO算法和GA-PSO算法都達到了較好的效果，相對來說，GA-PSO算法達到更好的控制效果。俯仰角如圖5所示，標準PSO算法在0.1 s時有較大的波動，而GA-PSO能較快地達到穩定效果；偏航角如圖6所示，達到穩定時間GA-PSO有明顯的改善，相差10倍左右，穩定性比標準PSO更好；翻滾角如圖7所示，達到穩定時間和穩定性相近。X軸方向如圖8所示，GA-PSO較快達到穩定狀態；Y軸方向如圖9所示，達到穩定時間和穩定的效果相近；Z軸方向如圖10所示，GA-PSO穩定性較好；達到穩定時間比PSO快。經過對飛行器PID優化，得出PID各參數的值，如表1所示。各項數據表明，各項指標在同行研究中達到領先水平，表明本文提出的GA-PSO算法在飛行器中達到了優化的效果。

飛行器在實際飛行中，會受到各種信號的干擾和風力的影響，導致飛行器的位置和姿態角發生變化，因此在仿真中加干擾信號進行測試，在1 s，2 s,3 s的時間給姿態角加一個隨機干擾突變信號，仿真結果如圖11所示，飛行器的姿態角在0～3 s時間內出現波動，范圍在0.7～1 rad之間，波動是非常大的，產生不穩定，但最終通過控制器的調節回到了穩定狀態。

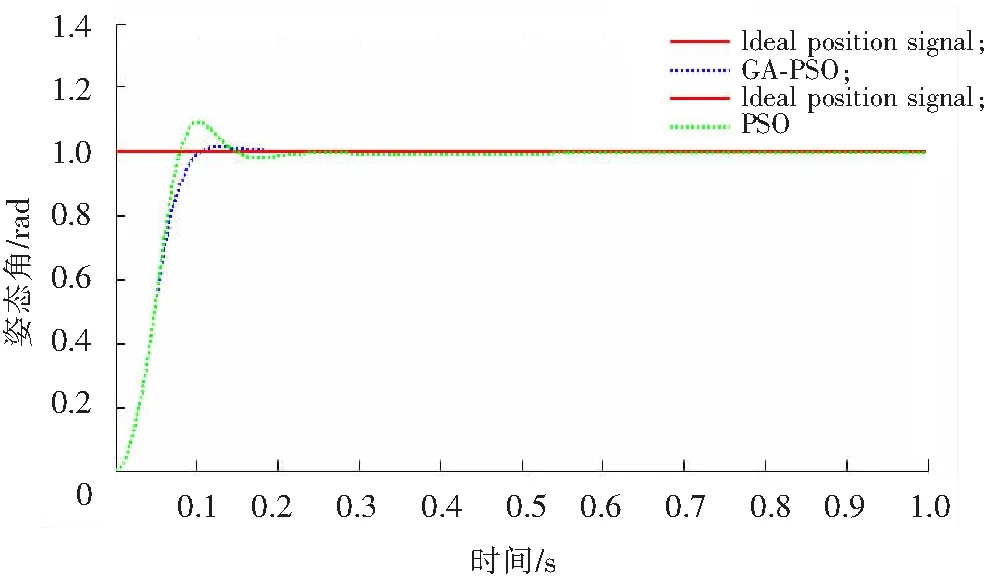
圖5 俯仰角Fig.5 Angle of pitch

圖6 偏航角Fig.6 Yaw angle

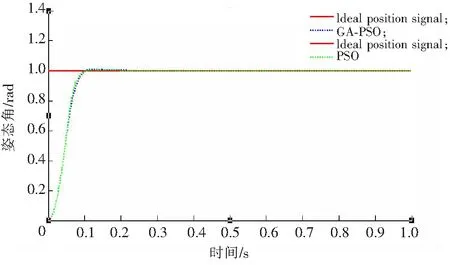
圖7 翻滾角Fig.7 Rolling angle

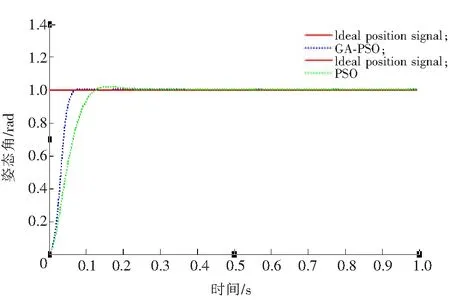
圖8 X軸方向Fig.8 X direction

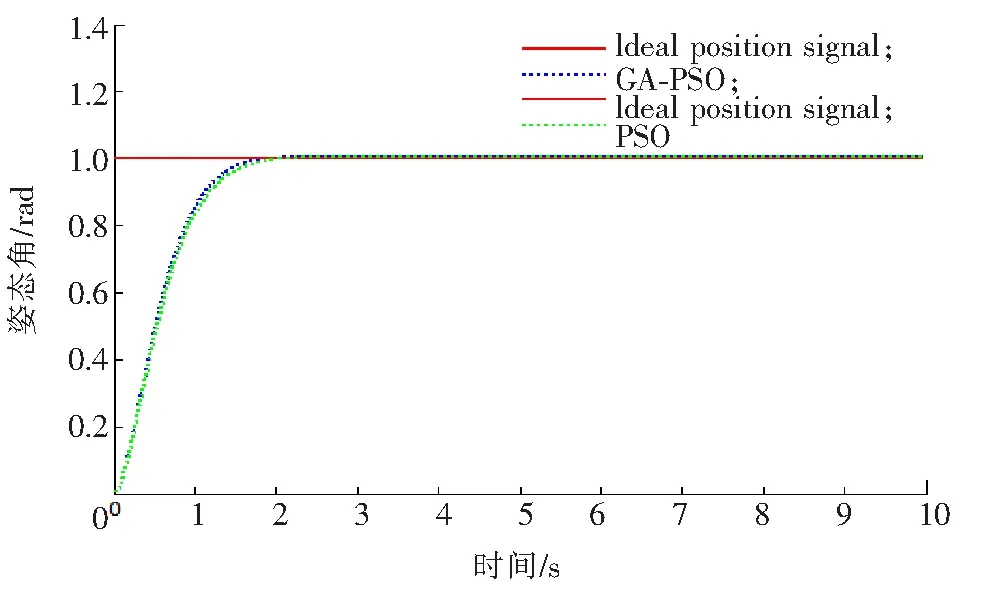
圖9 Y軸方向Fig.9 Y direction

圖10 Z軸方向Fig.10 Z direction

實驗室的飛行控制器部分的結構如圖12所示，飛行器姿態控制是通過PID參數的設置來達到飛行器的穩定效果，PID參數設置如表1所示，為了檢驗設計的效果，把表1數據應用于實驗室的飛行器，通過多次飛行試驗，測試數據如表2所示，達到較好的效果。

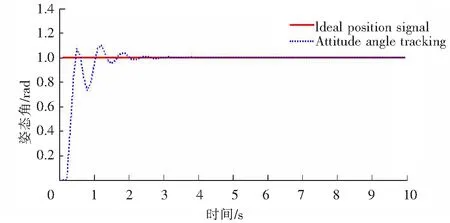
圖11 干擾信號仿真圖Fig.11 Interfering signal simulation diagram

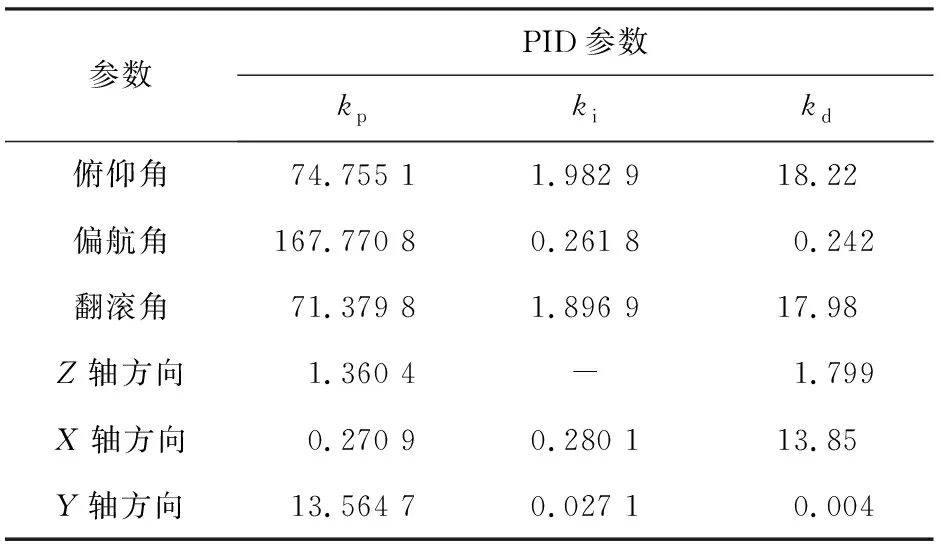
表1 PID參數優化表Tab.1 PID parameters optimization rad

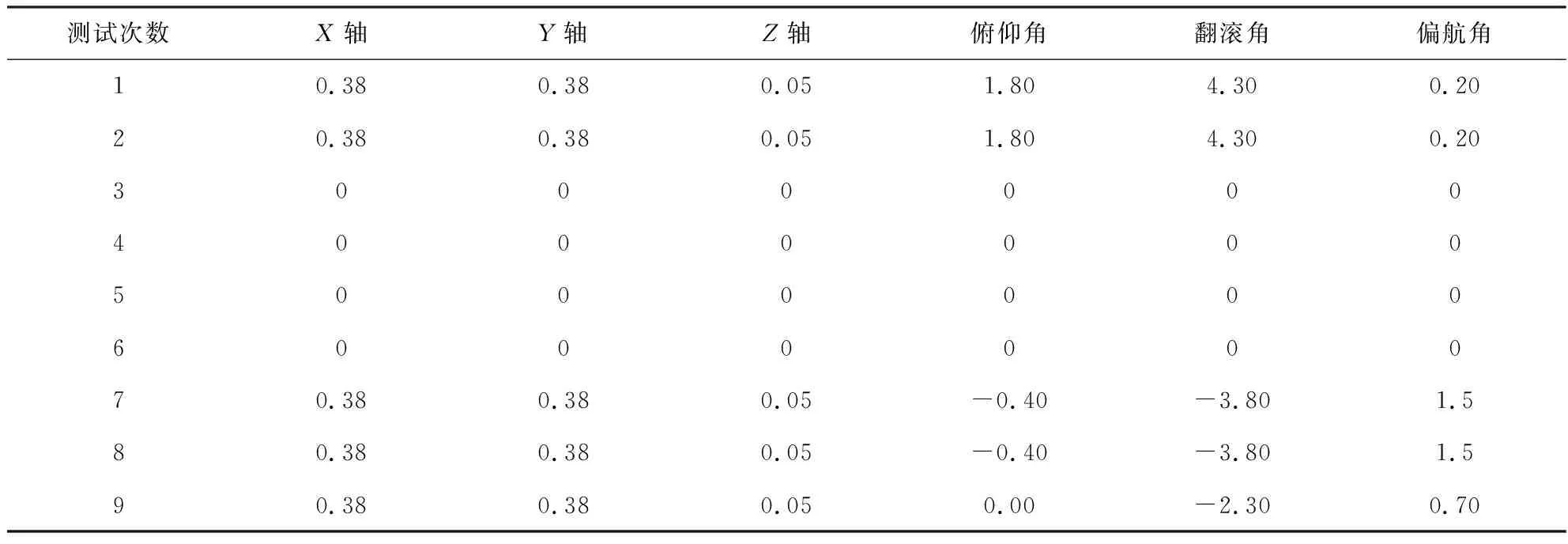
表2 飛行測試數據Tab.2 Flight test data rad

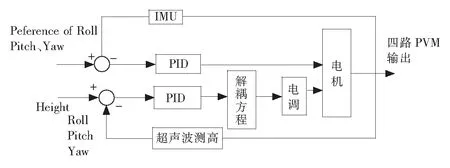
圖12 飛行控制器結構Fig.12 Structure of the quadrotor

4 結 語

通過對實驗室四旋翼飛行器進行建模，提出改進的GA-PSO算法，通過仿真實驗結果表明，飛行器達到穩定狀態快，精度高的特點。為了更好地驗證算法的效果，對飛行器進行多次試飛，測試數據表明，控制器具有較好的魯棒性和良好的控制效果。

參考文獻/References：

[1] 燕 翔，張持健.工業隨動系統中模糊PID控制器的設計與應用[J].河北工業科技,2011,28(2)：122-125.

YAN Xiang,ZHANG Chijian. The design and application of Industrial design of fuzzy PID controller in the servo system[J]. Hebei Journal of Industrial Science and Technology,2011,28(2):122-125.

[2] 宋 遙，李國名，徐 麗.采用蟻群算法模擬機器人尋路的仿真實驗[J].河北工業科技,2010,27(5)：340-343.

SONG Yao, LI Guoming, XU Li. The simulation experiment of ant colony algorithm simulation robot in pathfinding[J]. Hebei Journal of Industrial Science and Technology,2010,27(5):340-343.

[3] 劉金琨.先進PID控制MATLAB仿真[M].北京：電子工業出版社,2012.

LIU Jinkun. Simulation of Advanced PID Control and MATLAB[M].Beijing: Electronic industry press,2012.

[4] 黃溪流.一種四旋翼無人直升機飛行控制器的設計[D].南京：南京理工大學，2010.

HUANG Xiliu. Tontroller Design of Four-rotored Helicopters Flight[D].Nanjing：Nanjing University of Science and Technology,2010.

[5] MINH L D.Modeling and control of quadrotor MAV using vision based measurement[A].2010 International Forum on Strxtegic Technology(IFOST)[C].San:[s.n.],2010.70-75.

[6] SUBBARAO A K,LEWIS F.Dynamic inversion of quadrotor with zero-dynamics stabilization[A].IEEE International Conference on Control applications[C].San Antonio:[s.n.],2008.1 189-1 194.

[7] BOUABDALLAH S,SIEGWRT R.Design and control of quadrotors with application to autonomous flying[D]. Lausanne :EPFL,2006.

[8] 李 俊，李運堂.四旋翼飛行器的動力學建模及PID控制[J].遼寧工程技術大學學報,2012,31(1)：114-117.

LI Jun,LI Yuntang. Four rotor aircraft dynamics modeling and PID control[J]. Journal of Liaoning Technology University,2012,31(1):114-117.

[9] 胡海兵，胡慶波，呂征宇.基于粒子群優化PID伺服控制的設計[J].浙江大學學報(工學版),2006，40(12)：2 144-2 148.

HU Haibing， HU Qingbo， LYU Zhengyu. The design of based on particle swarm optimization PID servo control[J]. Journal of zhejiang University(Engineering Science),2006,40(12):2 144-2 148.

[10] 孫增圻.遺傳算法:智能控制理論與技術[M].北京：清華大學出版社,2011.

SUN Zenqi. Genetic Algorithm: Theory and Technology of Intelligent Control[M].Beijing: Tsinghua University Press,2011.