基于ANFIS的一類免疫聚類建模方法的研究

馮蘋蘋，屈寶存，李 燁

（遼寧石油化工大學 信息與控制工程學院， 遼寧 撫順 11300）

復雜的不明確的現(xiàn)實系統(tǒng)是一個多輸入多輸出系統(tǒng)，具有強時變、強耦合及非線性等特征。為了對控制系統(tǒng)進行有效的合理的控制，需要確定其精確的數(shù)學模型。

自適應模糊推理系統(tǒng)（ANFIS）是利用神經網(wǎng)絡的學習能力來逼近模糊推理系統(tǒng)的設計，ANFIS是一種基于有效輸入輸出數(shù)據(jù)的一種算法。成功獲得一個高可靠性和強魯棒性的ANFIS網(wǎng)絡在很大程度上依賴于過程變量的選取及用于訓練的有效數(shù)據(jù)對。神經網(wǎng)絡的缺點在于如果用于訓練的數(shù)據(jù)對不充足或者是沒有得到有效訓練時會缺乏泛化能力。通過合理選擇數(shù)據(jù)點的范圍及選擇合理的用于神經網(wǎng)絡訓練的數(shù)據(jù)對將會克服這一困難。應用交叉驗證達到數(shù)據(jù)的優(yōu)化，該方法的優(yōu)點在于能夠將測試過程簡化并且得到信息的最大化。

1 自適應神經模糊推理系統(tǒng)（ANFIS）建模算法

ANFIS采用自適應模糊網(wǎng)格法先確定模糊網(wǎng)格，后利用負反饋優(yōu)化網(wǎng)格，該方法的不足之處是隨著輸入變量的增加，導致的模糊規(guī)則數(shù)成指數(shù)倍的增長，致使學習難度增加[]1，為克服這種問題，本文選用的衍生出來的ANFIS模型來優(yōu)化隸屬度函數(shù)、模糊規(guī)則、數(shù)據(jù)的選取從而節(jié)省計算時間和減小均方根誤差。

1.1 ANFIS的結構

基于模糊推理的自適應網(wǎng)絡將神經網(wǎng)絡的自學習能力和模糊推理系統(tǒng)結合起來，假設系統(tǒng)有兩個輸入，輸出為f（圖1）。

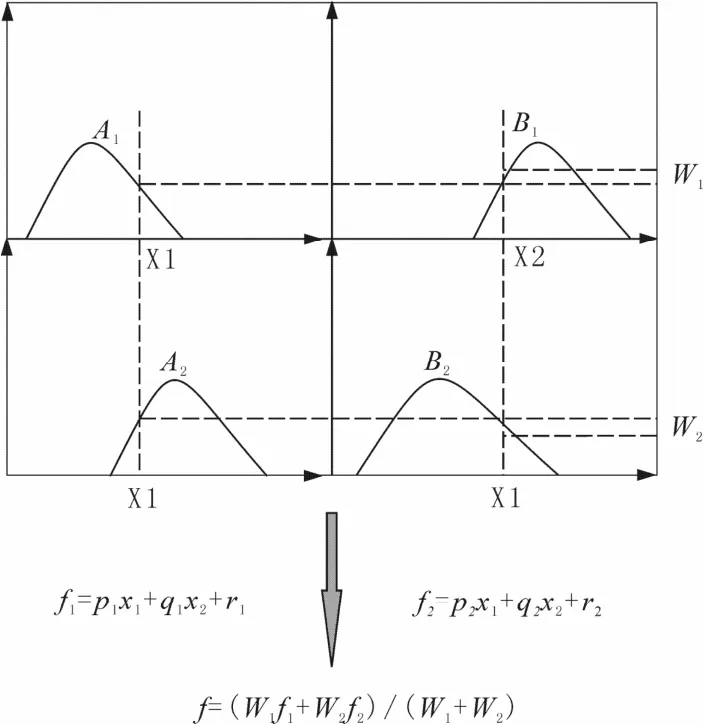
圖1 模糊推理機制Fig.1 Fuzzy inference mechanism

則T-S模型中得到兩條模糊規(guī)則如下：

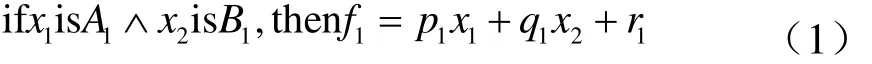
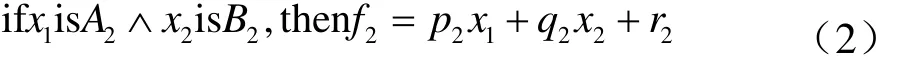
其對應的ANFIS的模型結構，如下圖2所示。

圖2 ANFIS的模型結構Fig.2 The structure of ANFIS

ANFIS模型的各層功能：

第一層:每個節(jié)點為自適應節(jié)點，對應的節(jié)點的傳遞函數(shù)為:

式中, j=1,2；i=n×m；O1為隸屬于模糊集Aj的隸屬度[1]。

根據(jù)需要選擇參數(shù)化隸屬函數(shù) μAj(xj)，本文選擇高斯型函數(shù)：

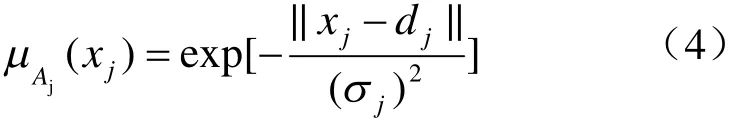
式中，dj和Oj為前提可變的參數(shù)。

第二層:該層計算每條輸入規(guī)則的激勵強度，一般情況采用乘法：

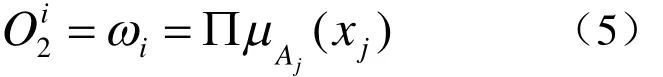
式中，j=1,2；i=1,2。

第三層:將每條規(guī)則的激勵強度歸一化。

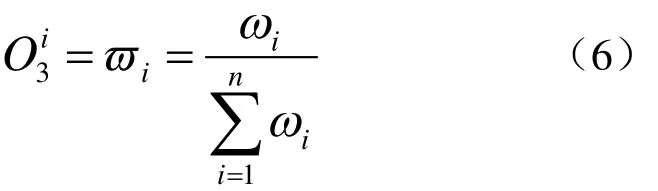
第四層:根據(jù)下面的公式計算每條規(guī)則對輸出的線性作用，公式為：

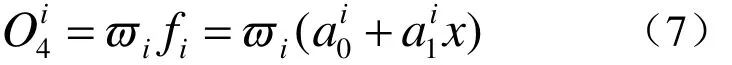
第五層:計算所有規(guī)則的總輸出：

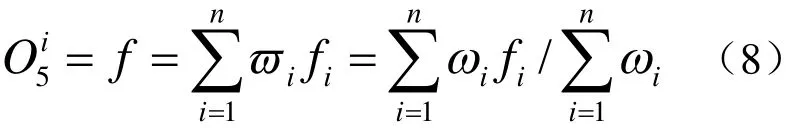
ANFIS模型采用混合學習算法，即對非線性參數(shù)采用反梯度下降法進行訓練，用遞推最小二乘法調節(jié)線性參數(shù)。在每次學習算法中，先固定前提參數(shù)[1]，采用遞推最小二乘法調整結論參數(shù)；然后計算出的數(shù)據(jù)的輸出誤差，從輸出節(jié)點反向傳入到輸入節(jié)點[2]，進而并對前提參數(shù)進行調整和優(yōu)化。

1.2 模糊結構辨識問題

ANFIS網(wǎng)絡屬于局部逼近網(wǎng)絡，與BP網(wǎng)絡相比還存在一定的差距，另外，T-S模糊模型要求線性的劃分輸入空間，所以對于較為復雜的非線性空間，要獲得較好的辨識效果，會致使規(guī)則數(shù)的增加。

針對上面提出的研究ANFIS的難題，更需要對輸入數(shù)據(jù)尋求好的聚類方法，然后對輸入空間進行合理的劃分，找到合適的規(guī)則數(shù)；提供恰當?shù)某跏季W(wǎng)絡參數(shù)值，減小其陷入局部極小的可能性，提高網(wǎng)絡的逼近效果，這就是模糊結構辨識的問題。

2 基于人工免疫的聚類算法

2.1 免疫聚類算法分析

基于脊椎動物免疫系統(tǒng)的人工免疫系統(tǒng)是對自然免疫系統(tǒng)的模仿，同生物進化過程不同的是，脊椎動物的免疫系統(tǒng)是產生合適的抗體并且消除抗原的演化過程。免疫系統(tǒng)的主要功能是識別體內的所有細胞是自己或是異己，然后進一步確認異己細胞激活免疫系統(tǒng)。抗體與抗原的相互結合，使免疫系統(tǒng)產生記憶細胞，并將同抗原的接觸記憶下來。在人工免疫原理的聚類算法分析中，抗原為需要聚類的數(shù)據(jù)，聚類中心視為免疫系統(tǒng)的抗體，對數(shù)據(jù)對象的聚類相當于免疫系統(tǒng)產生抗體、識別抗體，最后產生出最佳抗體的過程[3]。該聚類算法的動態(tài)流程圖如下圖3所示。

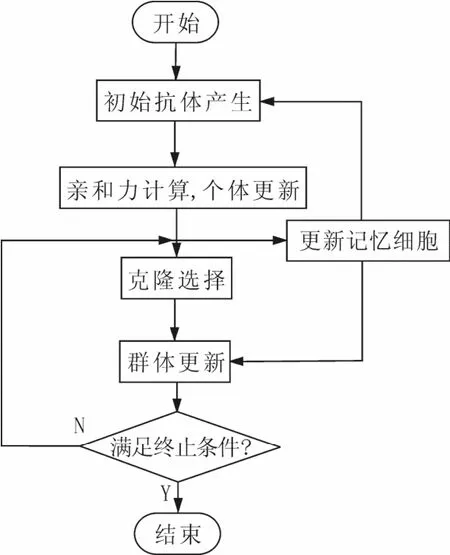
Fig.3 The dynamic flow chart of artificial immune圖3 免疫聚類算法的動態(tài)流程圖clustering algorithm

（1）定義需要聚類的輸入數(shù)據(jù)X[n]為抗原，n為輸入數(shù)據(jù)對的個數(shù)。

（2）在數(shù)據(jù)集Xi[i=1,2,…,n]中隨機選取k組數(shù)據(jù)，產生k個聚類中心，即在該空間中產生了k個抗體，抗體用來識別及捕獲臨近空間的抗原。

（3）計算反應抗原與抗體、抗體與抗體之間相似度的親合力及個體更新，選擇歐距氏離為親和力指標，定義抗原的分組判斷函數(shù)為：

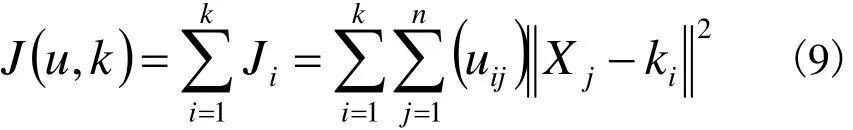
這里uij是向量Xj屬于ki(i=1,2,…,k)的程度，它的值在0和1之間。在每次分組時根據(jù)親和力屬于不同的 ki(i=1,2,…,k)。

（4）根據(jù)aiNer免疫網(wǎng)絡中有向搜索來尋找抗體優(yōu)化的方法，由公式 K=K-α(K-X)及計算出的親和力的大小來重新選擇最佳抗體[5]。其中K代表抗體，X代表抗原，α代表學習率。

（5）根據(jù)抗體抑制理論：當新抗體產生時，保留每組中的最優(yōu)秀抗體并清除其它所有不佳抗體。

反復進行上述(1)—(5)的步驟，直到滿足設定的目標要求。

3 仿真實驗

為了驗證本文中所提方法的有效性，引用文獻[5]中的一個函數(shù)的逼近問題的例子，函數(shù)式為：

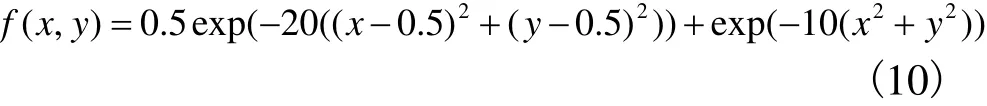
其中輸入變量x和y都定義在上，每個變量都按均勻的概率密度函數(shù)隨機的產生，函數(shù)產生 400個輸入輸出對作為訓練數(shù)據(jù)。試驗中，如下所述設置各個學習參數(shù)：最大訓練步數(shù)為3 000，學習率為0.003，慣性系數(shù)為0.51，合成時刻的誤差，目標誤差，預設閾值。

先利用人工免疫聚類算法對數(shù)據(jù)進行聚類，當聚類數(shù)為15時函數(shù)的有效值最大，因此建立的初始模糊規(guī)則庫中包含15條模糊規(guī)則。接著按照所需算法調整規(guī)則參數(shù)和網(wǎng)絡權值，為進行網(wǎng)絡結構的優(yōu)化，當計算誤差小于合成誤差時，除掉那些影響最小的節(jié)點，以獲得更好的控制規(guī)則數(shù)目和網(wǎng)絡參數(shù)，達到函數(shù)的最佳逼近效果。

圖4 函數(shù)逼近結果Fig.4 Function and it's approximation results

4 結 論

從生物處理信息的機制中感受啟發(fā)，借助其較強的學習、記憶及自適應調節(jié)的能力，把人工免疫系統(tǒng)的原理應用于數(shù)據(jù)聚類分析的研究中，用來提取和優(yōu)化模糊規(guī)則的數(shù)目，從而進行模糊辨識。該方法提供的初始化方案為克服ANFIS網(wǎng)絡自身的缺陷提供了一個有效的途徑。

［1］ 王洪瑞,張永興,劉聰娜．基于ANFIS的機器人系統(tǒng)建模的研究[J].控制工程，2010，9(1)：55-58．

［2］童樹鴻, 沈 毅,劉志言.基于聚類分析的模糊分類系統(tǒng)構造方法[J].控制與決策.2001,16(11):737-744.

［3］張利平,吳秀玲.基于人工免疫的聚類算法的圖像檢索技術研究[J].情報探索,2010,18(2):18-21.

［4］王莉.人工免疫的圖像聚類算法的研究[D].太原:太原理工大學,2007:38-42.

［5］陳文清.基于免疫機理的水泥生產工藝故障智能診斷方法的研究[D].武漢：華中科技大學,2011:17-31.

［6］郝敏.基于模糊聚類算法的自適應模糊神經網(wǎng)絡研究[D].哈爾濱:哈爾濱理工大學,2007:12-17.