仿真技術在滾動阻力測試設備研發中的應用

張紹國 高 峰 徐國艷 崔 瑩

(北京航空航天大學 交通科學與工程學院，北京100191)

滾動阻力是輪胎滾動時與路面接觸變形產生的遲滯能量損失，以發熱為主要形式發散到大氣中.降低輪胎的滾動阻力可以節約油耗，減少溫室氣體排放.歐盟和美國等國家頒布的輪胎標簽法規對輪胎滾動阻力提出了分級要求，不滿足滾動阻力認證的輪胎禁止在相關國家銷售［1］.

輪胎結構設計中的能量損耗模型主要對輪胎的滾動阻力進行預測分析，尋求減少滾動阻力的結構設計方法，但不能滿足輪胎的認證需求［2-3］.滾動阻力測試是高負荷下測量小分力的試驗，早期的輪胎滾動阻力試驗在底盤測功機上通過反拖法進行［4］，室內專用的單滾筒大直徑測試設備，對控制和測試精度要求較為嚴格，高精度的多分量傳感器和合理的定位誤差補償算法直接影響著設備的產品質量.本文基于輪胎滾動阻力專用檢測設備的結構原理，建立了滾動阻力的動力學測試模型，模擬設備各種工況下的測試過程，并利用正交回歸擬合算法對測試數據進行誤差修正，最后與試驗數據進行對比驗證.

1 測試原理與誤差分析

1.1 測試方法

設備采用轉鼓式結構，GB/T 18861—2002及ISO 28580等滾動阻力試驗標準中規定滾動阻力測試方法包括測力法和測扭矩法等［5］.由于轉鼓的起動扭矩要比穩速運轉扭矩大得多，且測量必須在無加速扭矩輸入時進行，測試上難于實現，精度很難保證，故現在國外設備滾動阻力的計算模式多采用測力法，測試原理如圖1所示，通過測量輪胎軸上的反作用力以避免轉鼓轉動慣性對測量結果的影響［6］.滾動阻力和滾動阻力系數換算公式如式(1)和式(2)所示.

式中，Fr為輪胎滾動阻力;Ft為輪軸反作用力;L為輪軸中心到轉鼓面的距離;R為轉鼓半徑.

式中，Cr為輪胎滾動阻力系數;Fy為輪胎負荷.

圖1 滾動阻力測試原理圖

1.2 設備原理

設備主要有床身、轉鼓、徑向加載裝置和輪軸裝置等組成，如圖2所示.旋轉的輪胎與轉鼓之間的接觸壓力使輪胎產生變形，并在接觸點的切線方向產生了滾動阻力，通過輪軸的反作用力傳遞給傳感器板.

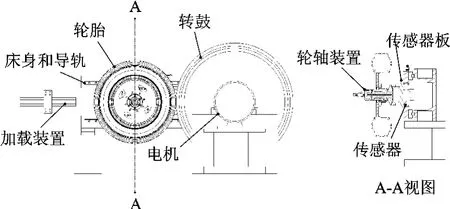
圖2 試驗設備結構圖

1.3 誤差分析

設備的安裝精度直接影響測試數據的可靠性.機械定位誤差包括輪軸作用方向與轉鼓接觸中心平面的對中誤差;輪軸的中心平面與轉鼓的接觸中心平面的垂直誤差(外傾角);輪軸的行進方向與轉鼓中心平面方向間的夾角(側偏角).輪軸與轉鼓基準線的對中偏差使輪胎負荷在滾動阻力方向產生偏移分量，影響測試數據精度，是設備的主要誤差源.

設備的系統誤差還包括傳感器零點漂移以及軸承摩擦等，這些因素產生的縱向力視為附加損失處理，可以通過設備標定消除，本文重點對設備對中定位誤差進行討論，數據的誤差修正算法按照式(3)進行處理.

式中，Fm為輪軸力測量值;Fd為動態誤差.

2 三分力傳感器

2.1 傳感器結構

設備的試驗數據通過傳感器測量輪軸力來實現，高精度的三分力傳感器是設備測試系統核心部件.靈敏度、維間耦合等因素與傳感器的性能密切相關，基于有限元的傳感器模型具備結構基準坐標明確和對稱性好等優點，目前國內外已經采用有限元方法對傳感器進行結構設計［7］.

十字型結構傳感器的主要變形部分由4個十字型筋和4個浮動支撐薄片組成，如圖3所示.在力的作用下，與力方向垂直的支撐薄片可以自由活動，該方向的十字型筋沒有變形，而與力作用方向垂直的十字型筋則發生彎曲變形，從而避免維力之間的干擾.通過分析應變區域彈性體的應變分量，將力分解為各自獨立的坐標成分，計算得到彈性體網格區域的應變量.

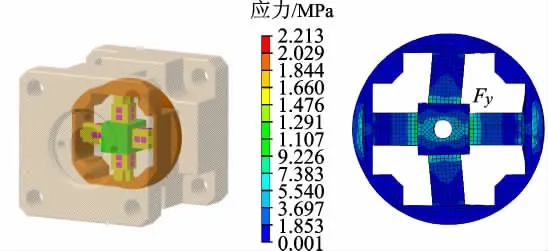
圖3 傳感器結構和有限元模型

2.2 模擬標定

傳感器滾動阻力方向的標定方式采用砝碼作為力源加載.4個靈敏度完全一致的傳感器以測力板形式與設備裝配在一起，傳感器分別安裝在臺架和傳感器板之間對應的角部位置，命名為D1，D2，D3，D4，如圖4所示.

圖4 傳感器布置方案

靜負荷下，在法蘭參考點沿滾動阻力方向分別施加大小不同的負載，同時采集4個傳感器的應變量作為樣本數據，按式(4)對數據進行和差處理得到總應變量D，標定數據如表1所示.

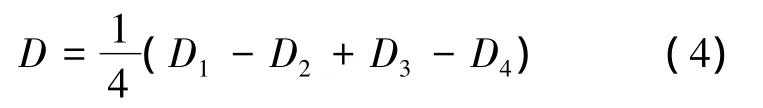
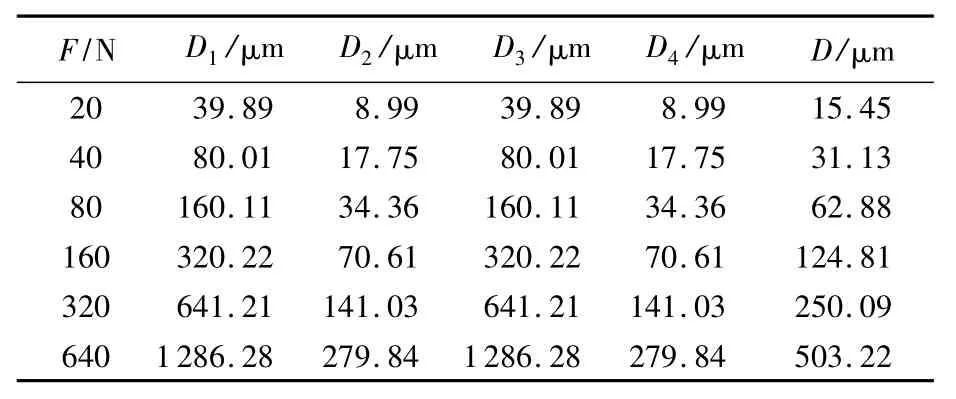
表1 滾動阻力方向標定數據

依據最小二乘法對采集的傳感器樣本數據進行計量單位轉換，應變量D和力F的擬合方程為

式中，k，b為回歸系數;計算求出 k=1.27;b=0.23.

3 測試模型

3.1 輪胎有限元模型

輪胎以某成品胎11R22.5為研究對象.輪胎中的橡膠大部分填充碳黑材料，采用Yeoh三次方程，如式(6)所示.

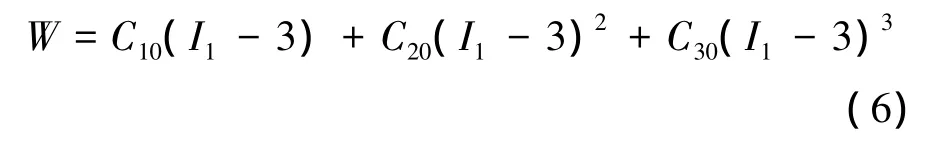
式中，W為橡膠的應變能函數;I1為第一應變不變量;C10，C20，C30為常數.

結構阻尼能夠很好地描述輪胎滾動時的遲滯特性，為限制測試過程中產生的數值振蕩，提高計算精度，輪胎模型采用結構阻尼模型［8］.

式中，M為質量矩陣;P為外力;K為剛度矩陣常數;C為阻尼矩陣常數.

滾動阻力分析中要考慮熱力耦合現象［9-10］.計算輪胎的溫度場分布時，主要考慮胎體熱源與輪胎外界的熱交換.輪胎的有限單元網格熱能Q由式(8)計算［11］.

式中，σp和εp分別為單元應力和應變量;ω為輪胎滾動角速度;tanδ為對應材料的損耗正切值.

3.2 邊界條件

在輪輞和輪軸裝置之間設置鉸接屬性，使輪胎在輪軸上具有旋轉自由度.輪胎的轉動通過轉鼓驅動.穩態條件下，通過對轉鼓施加恒定速度，驅動輪胎以設定速度做旋轉運動.圖5為輪胎在穩態條件下的計算模型.

圖5 滾動阻力測試模型

4 試驗驗證

單胎多點測試數據重復性精度決定著設備的測試能力.輪軸在大負荷作用下產生變形，加載方向與轉鼓中心線產生一定偏離，負荷對輪軸力Ft產生橫向干擾，同時由于控制精度等因素設備產生了系統累計誤差Fd.試驗數據在美國MTS公司轉鼓式輪胎滾動阻力試驗機上進行，如圖6所示.輪軸與轉鼓軸中心基準位置標定偏差為0.04°，為保證設備測試精度，需對測試數據進行補償.

圖6 滾動阻力試驗

4.1 修正模型

測力法通常采用輪胎正反轉，用二者輪軸力的平均值作為補償結果，但正反轉測到的輪軸力差異較大，補償精度較低.有限元模型能夠模擬設備各種理想狀態下的工作特性，從而建立合理的誤差補償模型.圖7為額定工況下輪胎基準位置和偏差位置測試數據對比曲線，在偏差狀態下，負荷對滾動阻力方向測得的輪軸力產生干擾，因而偏差位置的測試數據幅值波動較大，與基準位置的數據產生一定差異.

圖7 滾動阻力應變波形

一次正交回歸試驗可以建立試驗指標與多個試驗因素之間的一次回歸關系，具有在每個試驗點獲得最大有用信息的特點，使統計分析具有較優性質.

采用L8(27)正交表進行試驗，對設備各控制因素進行上、下水平編碼，編碼如下:

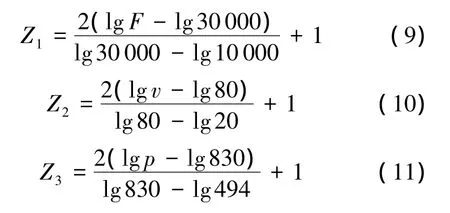
式中，v為試驗速度;p為氣壓.

按照不同工況下進行水平試驗，測試數據如表2所示.經過編碼后建立各控制參數和測試結果的一元正交回歸方程如下:

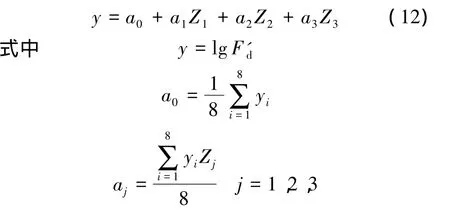
其中，F'd為在仿真模型中得到的誤差值.

表2 正交試驗數據

由表2得:a0=0.435，a1=0.359，a2=0.029，a3=-0.056.

方程的回歸系數不受試驗因素量綱和數值的影響，回歸系數反映該因素影響的大小.代入回歸方程，化簡后得到指數方程(13)，公式表明負荷和胎壓對測試數據誤差值影響權重較大.

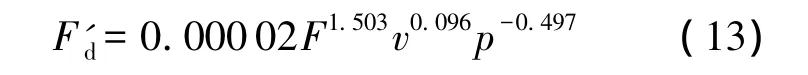
4.2 趨勢性試驗

圖8和圖9為額定速度下滾動阻力與負載和充氣壓力的變化關系，仿真結果和試驗數據的變化趨勢一致.輪胎滾動阻力與負載成正比關系，負載增加使輪胎變形變大，輪胎的內摩擦滾動阻力也隨之增大.

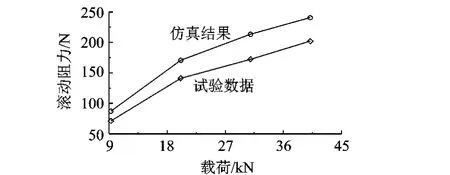
圖8 滾動阻力與負載變化關系

滾動阻力隨氣壓變大而減小，主要是氣壓升高使輪胎的胎體簾線張緊，剛度增大，相同負載下輪胎的下沉量減小，導致滾動阻力減小［12］.

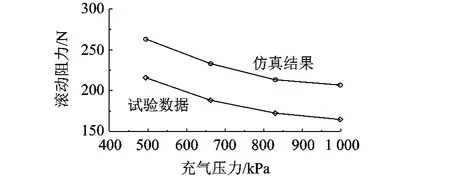
圖9 滾動阻力與充氣壓力變化關系

4.3 重復性試驗

ISO—28580中規定轎車和載重輪胎滾動阻力測試標準偏差不能超過0.2 N·kN-1，滿足此條件設備具備對輪胎進行質量分級的能力.由于精確的輪胎有限元模型構建困難，并且為提高計算效率，對測試模型進行合理簡化，將轉鼓、輪輞作為剛體部件處理，仿真結果比試驗數據高出20%左右.仿真結果和實驗數據之間的關聯模型如式(14)所示:

η受負載脈動、速度波動和閉氣工況等因素影響，由于變化范圍較小，體現在誤差數據上量值有限，為簡化計算，取平均值0.8.

式(13)不僅對定位誤差進行修正，還能夠消除設備由于控制精度等因素對測試數據產生的擾動.在MTS滾動阻力試驗設備上，對輪胎進行6次相同工況下的閉氣試驗，結果如表3所示.修正后滾動阻力系數試驗精度為0.0679，設備滿足趨勢性試驗標準要求.

表3 重復性試驗數據

5 結論

針對輪胎滾動阻力測試大負荷小分量的特點，通過建立設備的有限元測試模型，分析設備在各種狀態下的測試特性.計算結果表明，以測力板形式安裝的傳感器布局方案能夠實現對目標測試量的有效采集，在相同的控制參數下，仿真結果與試驗數據表征的趨勢特征一致.在設備現有工況的基礎上，利用一次正交回歸方程建立的誤差補償算法綜合考慮設備機械定位及控制精度等因素對測試數據產生的擾動，能夠減少系統的累計誤差，提高現有設備的測試精度.該結論為高性能輪胎滾動阻力測試設備的研制提供理論基礎和數據處理方法.

References)

［1］ Jerome B，Jason B.Reducing tire rolling resistance to save fuel and lower emissions［J］.SAE International Journal of Passenger Cars-Mechanical Systems，2009，1(1):9-17

［2］ Jun A，Chen J F，Michael Rotter J，et al.Assessment of rolling resistance models in discrete element simulations［J］.Powder Technology，2011，206(3):269-282

［3］ Shida Z，Koishi M，Kogure T，et al.A rolling resistance simulation of tires using static finite elements analysis［J］.Tire Science and Technology，1999，27(2):84-105

［4］ 王建強，何鳳江，張立斌，等.汽車動力性檢測模型的建立［J］.中國公路學報，2001:14(3):109-112 Wang Jianqiang，He Fengjiang，Zhang Libin，et al.A model for testing automobile dynamic property［J］.China Journal of Highway and Transport，2001，14(3):109-112(in Chinese)

［5］任禮行，劉青，張艾謙，等.輪胎滾動阻力測量與分析［J］.汽車工程，2000，22(5):316-319 Yam Laihang，Liu Qing，Zhang Aiqian，et al.Measurement and analysis of tire rolling resistance ［J］.Automotive Engineering，2000，22(5):316-319(in Chinese)

［6］韓秀芝.子午線輪胎穩態滾動阻力及水滑特性的研究［D］.北京:北京化工大學機電工程學院，2009:7-10 Han Xiuzhi.Research on steady-state rolling resistance and hydroplaning of radial tire［D］.Beijing:School of Mechanical and Electrical Engineering，Beijing University of Chemical Technology，2009:7-10(in Chinese)

［7］王國泰，易秀容，王理麗.六維力傳感器發展中的幾個問題［J］.機器人，1997，19(6):447-478 Wang Guotai，Yi Xiurong，Wang Lili.Problems related to the development ofsix axes force/torque sensor［J］.Robot，1997，19(6):474-478(in Chinese)

［8］管迪華，曾祥生，范成建.輪胎動態模型的阻尼和對滾動阻力及動態響應影響的分析［J］.汽車工程，2006，28(7):643-646 Guan Dihua，Zeng Xiangsheng，Fan Chengjian.Measurement and analysis of tire rolling resistance［J］.Automotive Engineering，2006，28(7):643-646(in Chinese)

［9］ Lin Y J，Hwang S J.Temperature prediction of rolling tires by computer simulation［J］.Mathematics and Computers in Simulation，2004，67(3):235-249

［10］ Yin H S，Hu Y S，Zhang H，et al.Truck tire thermal-mechanical FEA and DMA with application to endurance evaluation［J］.Tire Science and Technology，2006，34(4):220-236

［11］龔科家，危銀濤，葉進雄.基于熱力學有限元分析的輪胎滾動阻力仿真［J］.中國機械工程，2009，20(5):626-629 Gong Kejia，Wei Yintao，Ye Jinxiong.Simulation techniques of tire rolling resistance based on thermal-mechanical FEA［J］.China Mechanical Engineering，2009，20(5):626-629(in Chinese)

［12］莊繼德.汽車輪胎學［M］.北京:北京理工大學出版社，1995:180-183 Zhuang Jide.Vehicle tire study［M］.Beijing:Beijing Institute of Technology Press，1995:180-183(in Chinese)