Sinc-Chebyshev配置方法求解一維對流擴散方程
毛 志
( 銅仁學院 數學與計算機科學系,貴州 銅仁 554300 )
一、引言
對流擴散方程(convection diffusion equation)是一類基本的運動方程,是描述粘性流體的非線性方程的線性化模型方程。它可以用來描述空氣動力學、水力學、環境保護和生物、化學工程等眾多科技和工程領域中的對流擴散問題[1],所以關于對流擴散方程數值方法的研究具有十分重要的理論價值和現實意義。對流擴散問題的有效數值解法一直是計算數學中重要的研究內容。由于對流擴散方程同時含有對流項和擴散項,在數值求解時會引起數值振蕩和數值彌散[2],使得方程的求解比較復雜。目前,求解對流擴散方程的數值方法有多種,如有限差分法(FDM)[3]、有限元法(FEM)[4][5]、有限體積法(FVM)[6][7]、邊界元法(BEM)等,其中有限差分方法是一種重要的數值計算方法。
目前對于常系數的對流擴散方程已有較多、較好的研究,而對于變系數的對流擴散方程的研究卻較少,需要對方程做一定的假設。但在實際應用中,比如耦合流場的對流擴散方程,則需要研究變系數的情形[8]。基于此,本文考慮如下變系數的一維對流擴散方程的初邊值問題,
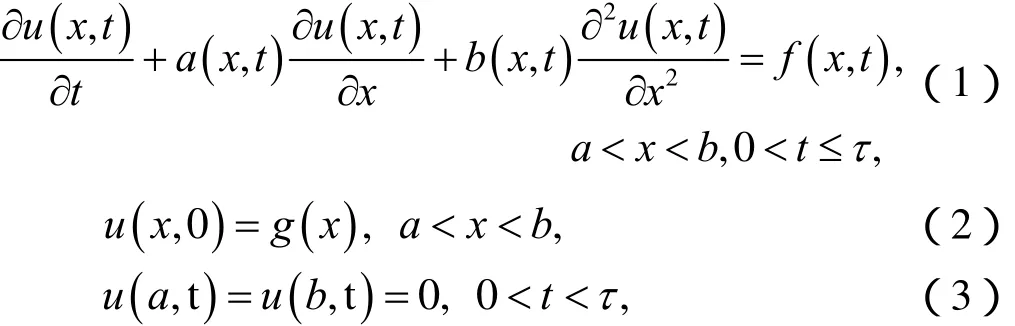
其 中a(x,t)、b(x,t)、f(x,t)和g(x)已 知 ,a(x,t ) ≠0、 b (x,t ) ≠ 0 且連續。
本文設計了一種新的求解上述問題(1)~(3)的數值方法---Sinc-Chebyshev配置方法。該方法是基于配置方法的。在空間方向和時間方向上,分別采用復合移位Sinc函數和移位Chebyshev多項式作為基函數,將方程(1)的未知解展開成一組具有未知系數的基函數和。通過選取相應的配置點后,原問題轉化為線性代數方程組的求解。充分利用復合移位 Sinc函數和移位Chebyshev多項式的性質,可高效地從線性代數方程組中解出未知系數。
二、Sinc函數和移位Chebyshev多項式
(一)Sinc函數
Sinc函數具有許多優良的性質[9][10],它被廣泛地用于數值分析及積分方程、常微分方程和偏微分方程的數值求解中[11][12][13]。
在整個實軸上,Sinc函數定義如下:
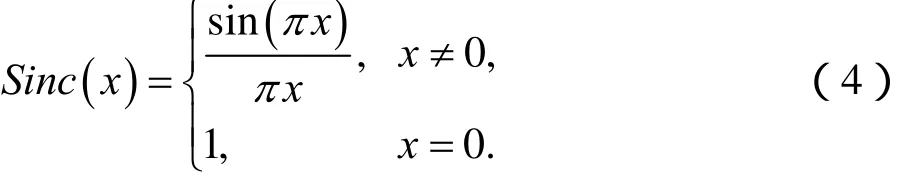
下面給出具有均勻網格節點的移位 Sinc函數的表達式:
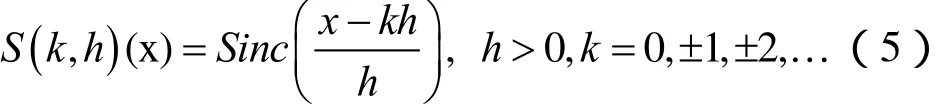
該函數在插值節點jx jh= 處有如下結論:

對于函數(),fxxR∈,若級數
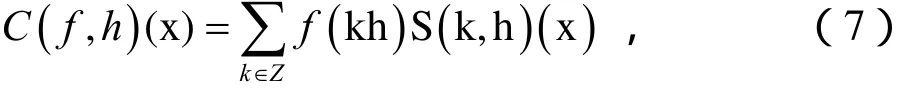
收斂,則稱之為Whittaker Cardinal function。
定理1 如果 f ∈Bh,其中Bh為Paley-Wiener類函數,則;進一步,若),則
由于本文所討論的問題是在有限區間上,故考慮如下的一一映射,

該映射將區間[a, b]--- 映射到(-∞ , +∞ )。記映射φ的逆映射為ψ = φ-1,在它的作用下,R上均勻網格點{kh}k∈Z的象為:
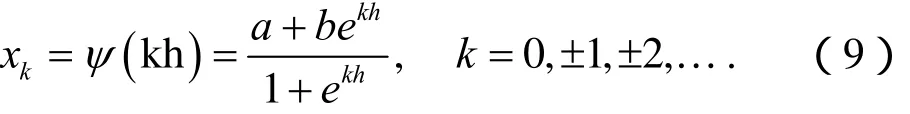
于是,需在區間[a, b]上取復合移位Sinc函數
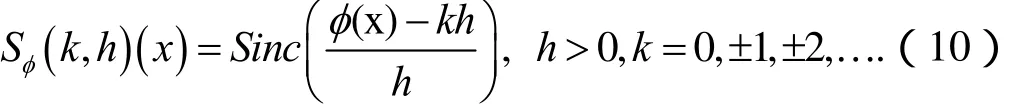
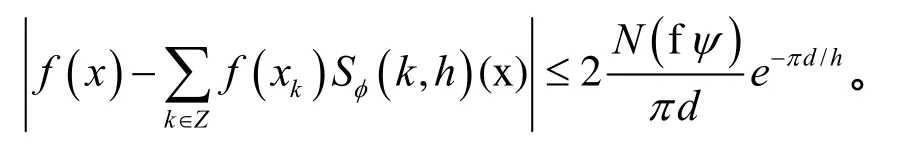
上面的結論顯示,對于 Bh上的函數,使用Sinc插值可達到指數收斂。為了構造 Sinc-Chebyshev配置方法,需要給出復合移位Sinc函數 Sφ(k, h ) (x)在節點 xk= ψ (kh), k = 0 ,± 1 ,±2 ,… 的各階導數值,
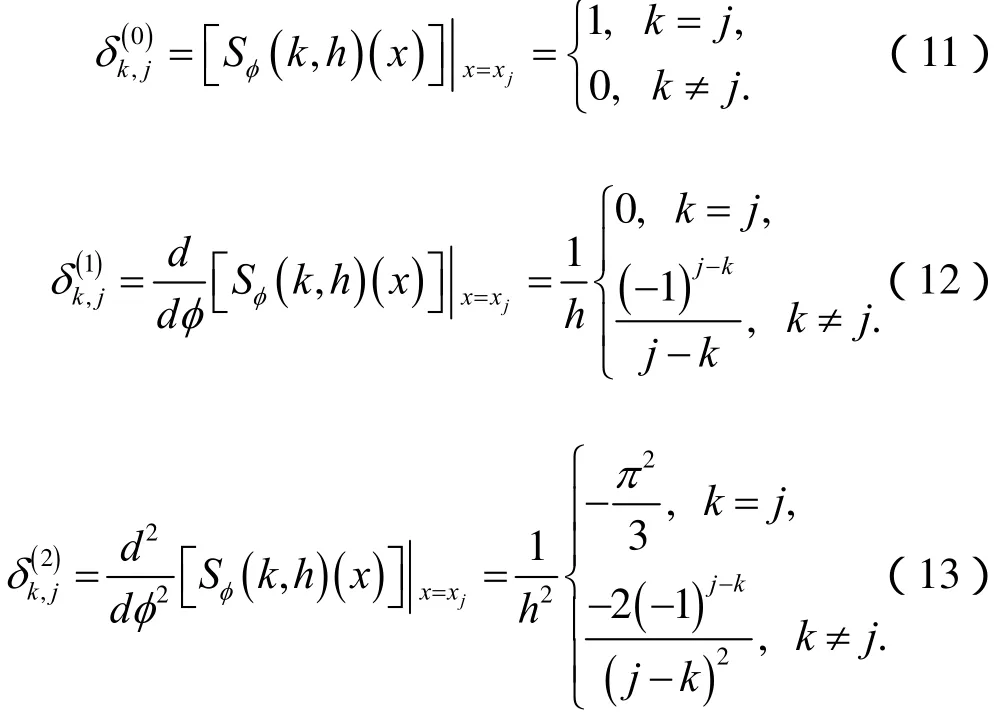
(二)移位Chebyshev多項式
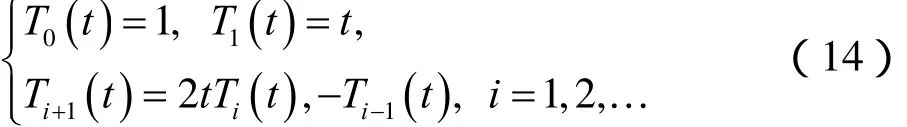
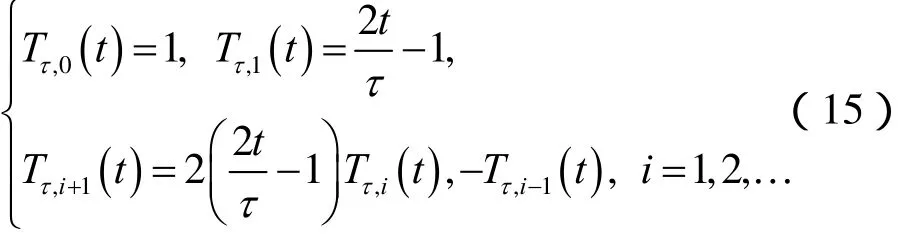
定理3 移位Chebyshev多項式 Tτ,i(t)的解析形式如下:
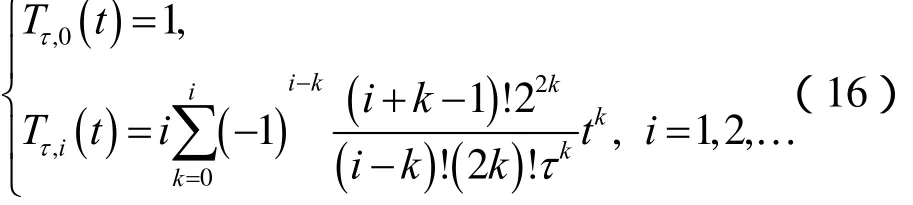
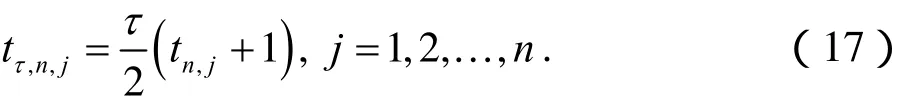
由于構造 Sinc-Chebyshev配置方法的需要,給出移位Chebyshev多項式 Tτ,i( t),i = 0 ,1,2,… 的一階導數,

三、Sinc-Chebyshev配置方法
為了求解問題(1) ~ (3),我們首先通過2 m +1個復合 移位 Sinc函 數Sφ(k, h ) (x) , k = 0,±1,±2,… ,±m 和n+1個 移 位Chebyshev多項式 Tτ,i(t),i = 0 ,1,2,… ,n 逼近u(x,t)。具體如下:
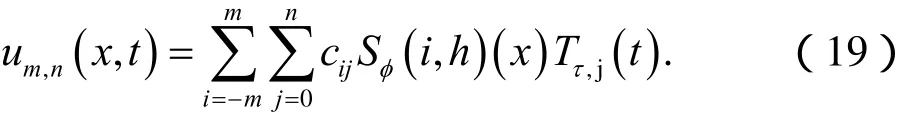
引理 1 取復合移位 Sinc函數的配置點為xk,k =0,±1,±2,… ,±m(表達式(9)),有如下關系成立:
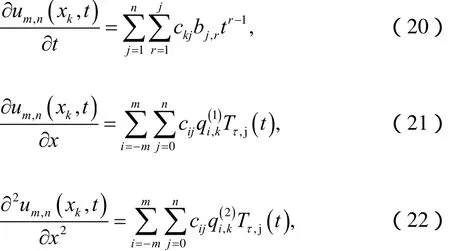
下面求解問題(1) ~ (3)。將表達式(19)代入方程(1)中可得,
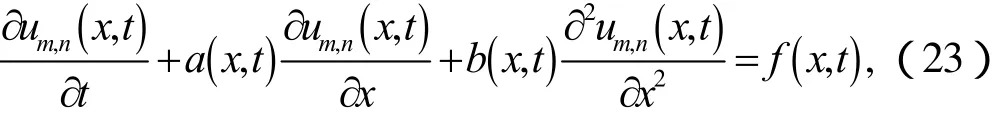
在上述表達式(23)中,我們選取配置點分別為xk,k =0,±1,±2,… ,±m(表達式(9))和tτ,n,j,j = 1,2,…,n(表達式(17))。根據引理1可得,
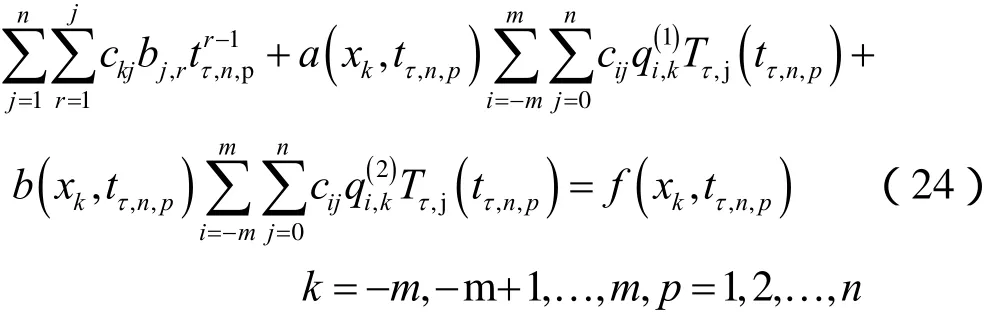
將表達式(19)代入初始條件(2)中可得,
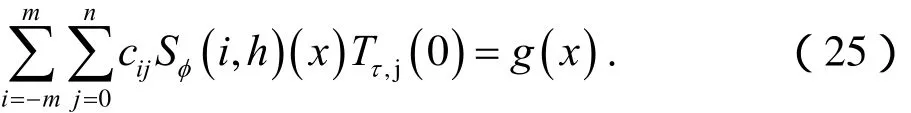
將上述表達式(25)在2 m +1個點 xk,k =0,±1,±2,…,±m上進行配置,并利用表達式(11)可得,
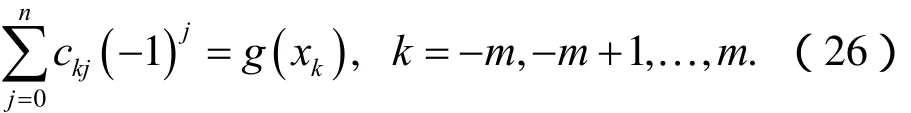
于是可從表達式(24)和(26)所構成的線性方程組中解出 (2 m + 1 ) (n+ 1 )個未知系數 cij,從而得到原問題(1)~(3)的數值解 um,n(x, t)。
四、總結
本文給出了一種求解對流擴散方程的Sinc-Chebyshev配置方法,它把求解對流擴散方程的初邊值問題轉化為解線性代數方程組。數值試驗結果顯示,該方法十分有效。下一步將嘗試把該方法用于分數階對流擴散方程[15]的求解。這與許多實際應用問題如DNA和蛋白質分子的傳輸[16]密切相關,具有較大的實用價值。
[1]汪繼文,李付鵬,竇紅.求解對流擴散方程的一種高分辨率有限體積-有限元方法[J].水動力學研究與進展,2012,27(3):339-347.
[2]薛禹群,謝春紅.地下水數值模擬[M].北京:科學出版社,2007,189-193.
[3]陸金甫,關治.偏微分方程數值解法(第2版)[M].北京:清華大學出版社,2003.
[4]Katsuhiro Sakai.A new finite variable difference method with application to locally exact mumerical scheme[J].Journal of Computational Physics, 1996,,124::301-308.
[5]WANG Ji-wen, LIU Ci-Qun. Local discontinuous Galerkin method for radial porous flow with dispersion and adsorption[J]. Applied Mathematics and Mechanics,2004, 25(9): 977-982.
[6]LU Biao, JIN Sheng, AI Cong-fang. A a conservative unstructured staggered grid scheme for incompressible Navier-Stokes equations[J]. Journal of Hydrodynamics,2010,22(2): 173-184.
[7]LEEL. . A class of high-resolution algorithms for incompressible flows[J].Computers and Fluids, 2010,39(6): 1022-1032.
[8]余亮.求解變系數對流擴散方程的一類新的LBGK格式[D].武漢:華中科技大學,2008.
[9]Lund J., Bowers K. .Sinc methods for quadrature and differential equations[M]. Philadelphia,SIAM,1992.
[10]F. Stenger. Handbook of Sinc numerical methods[M].New York, CRC Press,2011.
[11]Dehghan M., Saadatmandi A.. The numerical solution of a nonlinear system of second-order boundary value problems using the Sinc-collocation method[J].Math Comput Model,2007,46:1434-1441.
[12]Parand K.,Dehghan M.,Pirkhedri A. . Sinc-collocation method for solving the Blasius equation[J].Phys Lett A,2009,373: 4060–4064.
[13]Rashidinia J., Zarebnia M. .The numerical solution of integro-differential equation by means of the Sinc method[J].Applied Math Comput,2007, 188: 1124–1130.
[14]李慶揚,王能超,易大義.數值分析(第5版)[M].北京:清華大學出版社,2008.
[15]常福宣,陳進,黃薇.反常擴散與分數階對流-擴散方程[J].物理學報,2005,54(3):1113.
[16]Haw Yang, Guobin Luo, Pallop K.,Tai-Man Louie, Ivan Rech,Sergio Cova, Luying Xun,X.Sunney Xie.Protein conformational dynamics probed by single-molecule electron transfer[J].Science,2003,5643:262–266.

