水庫調洪數值—解析法的研究及其在福安市防洪排澇設計中的應用

李松興

（寧德市東閩水利水電勘察設計有限公司 福建寧德 352100)

水庫調洪演算大多采用試算法、圖解法或相關圖法。這些水庫調洪演算方法大都是通過對相關的水量平衡方程進行圖解和求解來實現的，相應的計算工作量大、效率低，在編程靈活性和計算精度等方面也存在一定的局限性。近期水庫調洪計算研究的重點是如何找到一種從理論與實用上滿足水庫在遭遇大洪水，水庫實時洪水調度計算所需的高精度、高速度，適合計算機計算使用的調洪計算方法。此方法不用試算，更無需迭代求解。水庫調洪數值解析解法就是這樣一種調洪計算方法，便于計算機用程序實現。本文從防洪調度方式復雜的水庫調洪計算出發，討論水庫調洪計算的主要內容，并探討基于水庫調洪數值—解析解法在福安市灣塢分區西片防洪排澇中的應用。

1 水庫調洪數值—解析解法

1.1 水庫調洪數值—解析解法原理

復雜情況下水庫調洪計算通常有兩種不同的求解情況：

（1)已知時刻tn-1的水庫水位Zn-1、入庫洪水流量Q(tn-1)、泄洪流量S(Zn-1)、水庫水面面積F(Zn-1)與時刻 tn的入庫洪水流量 Q(tn)，在一定的水庫泄洪設備類型、開啟寬度(或面積)的條件下，求解時刻tn的水庫水位Zn與泄洪流量S(Zn)。設hn為計算步長，hn=tn-tn-1。

(2)已知條件與情況(1)相同，求解水庫水位達到某一特殊水位 CR的時刻 tn，tn-1＜tn，hn=tn-tn-1。

根據水庫調洪計算的基本微分方程為∶

大連理工大學陳守煜教授提出調洪數值解法的四階龍格—庫塔公式為：

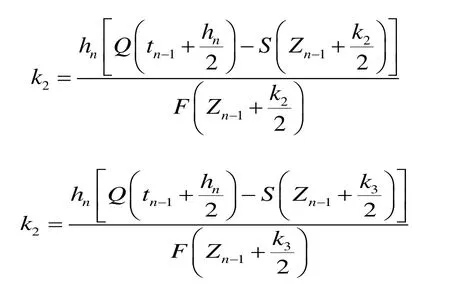
式中：Q(tn-1+hn/2)為時刻tn-1+hn/2的洪水流量；S(Zn-1+k1/2)、S(Zn-1+k2/2)、S(Zn-1+k3)分別為泄洪流量；F(Zn-1+k1/2)、F(Zn-1+k2/2)、F(Zn-1+k3)分別為水庫水面面積。

情況(1)可直接用四階龍格—庫塔公式求解。而水庫調洪數值—解析解法的基本思路是，對情況（1)的一般計算時段，用四階龍格—庫塔公式，對情況（2)的特殊計算時段用解析法求解，是復雜情況下調洪數值解法的拓展。

考慮到時刻tn-1，tn的入庫洪水流量Q(tn-1)，Q(tn)呈線性變化(增長或減少)，則時刻 tn的洪水流量 Q(tn)，可根據線性內插確定，將水庫調洪計算的微分方程變換為：

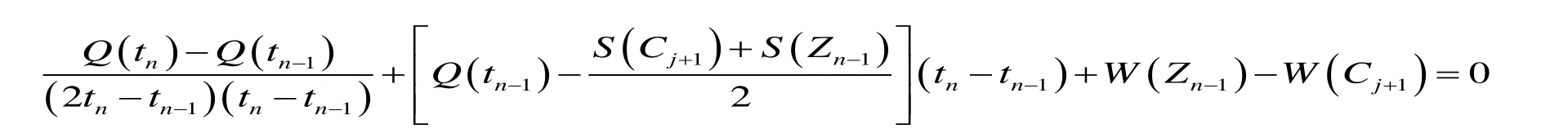
式中：W為水庫蓄水量。由二次方程的求根公式解得水庫水位達到特殊水位Cj+1的時刻tn的解析式為

滿足 tn-1＜tn，式中：

根據對水庫調洪過程的分析可知，確定式（1)根號前取符號的條件是δt> 0且δt＜tn-tn-1。情況（2)可直接根據公式（1)求解，不必試算。計算速度、精度、穩定性與四階龍格—庫塔調洪數值解法相當。

1.2 運用Visual Basic軟件編寫程序

1.2.1 數據載入

將諸如庫容曲線、洪水過程、不同泄洪建筑物及閘門開度對應的泄流曲線等數據賦值給相應的變量來進行計算。

1.2.2 結構模塊化

雖然面向對象的編程方法是當今的主流，但對以數值計算為主的程序仍常延用結構化的編程方法，把各個功能的模塊分開然后用主程序按需要調用，如插值模塊、下泄流量試算模塊、洪水演算進程模塊等部分，把它們分別寫成相對獨立的函數體并在主程序里調用。

2 福安市灣塢分區西片防洪排澇的調洪演算

2.1 工程概況

福安市地處寧德中部，位于福建省東北沿海，寧德市境內地形以丘陵山地為主，間以河谷平地和山間盆谷，全市海岸線長878km。

灣塢墾區地面庫 20年一遇最高洪水位的確定，考慮兩種組合即：（1)20年一遇洪水對應多年平均高潮位；（2)20年一遇高潮位對應于多年平均洪水，然后取這兩種組合的外包線。由于灣塢墾區地面庫具有一定的調蓄能力，故各墾區地面庫內最高水位的確定，必須通過調洪演算才能確定。

洪水主要通過原有的水閘泄入大海，當海潮水位高于滯洪區內水位時閘門關閉擋潮，反之則閘門開啟泄流排洪。

2.2 調洪演算

（1)20年一遇洪水對應多年平均高潮位。經調洪演算得各特征值見表1。

（2)20年一遇高潮位對應于多年平均洪水。多年平均年最大24h降雨130mm，3個滯洪區24h降雨總量分別為 26.3、54.1、87.6萬 m3，不考慮向外海排泄，全部留在滯洪區內（實際不可能)，此時對應滯洪區內的水位為3.46、3.25、3.02m。小于20年一遇設計洪水對應于多年平均最高潮位調洪后的塘內最高水位3.6m。

根據本地區水文雨潮組合分析，降雨的雨峰與白馬港高潮位遭遇的可能性較大，對規劃區防洪排澇偏不利。當出現設計重現期降雨時，潮汐高潮位重現期一般為多年平均。因此，規劃區洪澇重現期采用相應重現期的降雨與多年平均偏不利潮型組合。防洪工況按 20年一遇設計洪水對應多年平均高潮位。

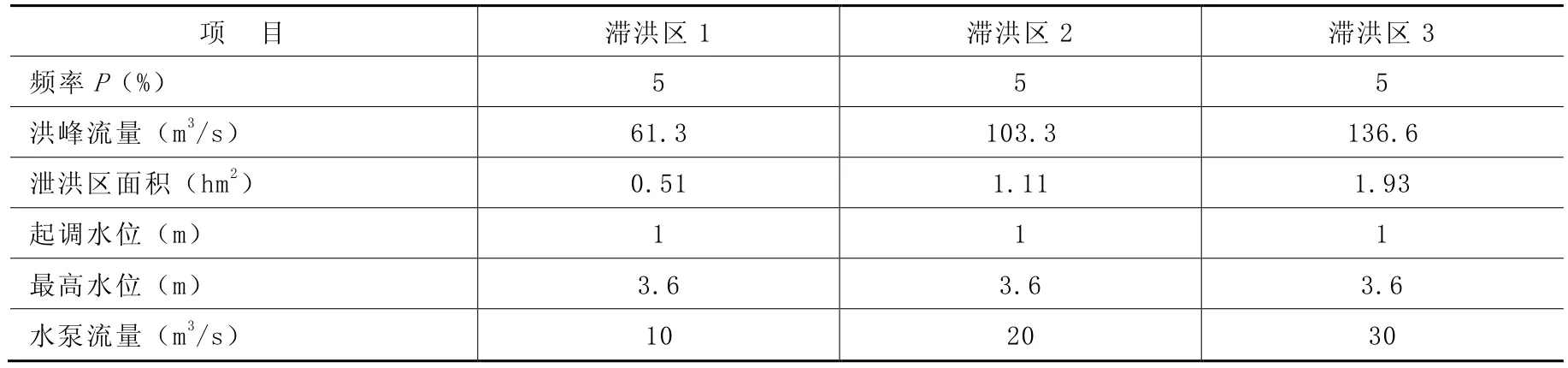
表1 特征值

3 結語

水庫調洪數值—解析解法是調洪解法的發展。它將復雜情況下調洪的兩種求解情況均用直接方法求解，不必用試算法，更無需迭代求解，從理論與實用上滿足了水庫在遭遇洪水情況下，水庫實時洪水調度計算所需的高速度與高精度的雙重要求。它為當前國內外迅速興起的水庫洪水調度自動化系統提供了理論嚴謹、計算速度快、精度高的復雜情況下水庫調洪計算模型。顯然，水庫調洪數值—解析解法必將廣泛應用于全國大中型水庫的洪水調節計算。

1 陳守煜.水庫調洪數值—解析解法.大連理工大學學報，1996，36(6)：721-724.

2 陳守煜.復雜情況下水庫調洪數值解法.大連理工大學學報，1995，35（4)：536-539.

3 李慶揚，王能超，易大義.數值分析〔M〕.華中科技大學出版社，1986.

4 陳守煜.水庫調洪數值解析法的理論、模式與程序.重慶交通學院學報，1983(1)：60-69.