某水電站邊坡卸荷巖體宏觀力學參數反演對比研究
蔡 健 ,劉 杰
(1.三峽大學土木與建筑學院,湖北 宜昌 443002;2.湖北省水利水電規劃勘測設計院,湖北 武漢 430064)
0 引 言
巖體宏觀力學參數在有限元計算中占有十分重要的地位,沒有正確的力學參數,數值模擬計算結果不能令人信服。由于巖體試驗尺寸及現場選點條件的限制,復雜巖體的力學參數很難通過室內外試驗直接測得。本文在總結前人研究成果的基礎上,基于巖體卸荷原理和分級分區方法的基礎上,對某水電站邊坡區域進行了合理的劃分,并選取具有代表性的區域進行二維與三維參數反演對比分析,最終得到卸荷巖體宏觀力學參數,并進一步驗證了本文研究方法的精確性和合理性。
1 基本方法
1.1 反演方法
以現場地質調查、材料試驗為基礎,與數值計算相結合,根據巖體結構面的分布狀況、級別及巖體的不同性質,對巖體力學參數采用分區分級計算,最終對整個工程巖體力學參數進行評價。具體計算步驟如下:
(1)根據工程地質勘探成果,對給定的整個工程巖體各個區域分區分塊。分區分塊主要考慮巖石的類型及強度、風化程度、地應力分布、結構面的產狀、間距及連通率、力學參數、地下水情況等。
(2)根據各個區塊內所含節理的尺寸,對各區塊劃分不同尺寸級別,數值模擬計算試塊全面、真實地反映其對應巖體的巖性組合和結構特征。
(3)根據每個區塊的邊界和外荷條件,對各區塊內的分級計算試塊逐級進行大三軸試驗數值模擬,對每個區塊的巖體參數進行評定。計算中應模擬區塊內每條裂隙、每個層面。對同一區塊不同級別計算試塊,計算順序是先小尺寸后大尺寸,先小裂隙后大裂隙。第1級試塊內為巖石和小節理裂隙材料,計算參數和本構關系直接采用室內試驗成果,通過第1級計算得到試塊材料的力學參數。第2級計算試塊內含第1級計算試塊材料和中等裂隙材料。根據以上方法,依次計算各區塊內不同級別的試塊,直至計算到該區塊最大級別試塊,最大試塊計算所得的參數就為該區塊的力學參數值。
(4)把各區塊和大斷層及軟弱厚層組合在一起,建立整體計算試塊,計算得到工程整體的力學參數,對整個工程的巖體進行評價。
1.2 計算公式
在主應力空間中,彈性狀態應力、應變關系服從廣義虎克定律。在平面應變狀態下,應變增量Δε3=0,計算模型在應力增量Δσ1、Δσ2的作用下,通過有限元計算可得到Δε1和Δε2,則可求出泊松比μ、變形模量E。由所求的變形參數,可得到單向應力狀態下的應變增量和應力增量之間的關系式。三維有限元分區分級參數模擬同二維有限元,根據廣義虎克定律推導出泊松比μ′和變形模量E′計算公式為
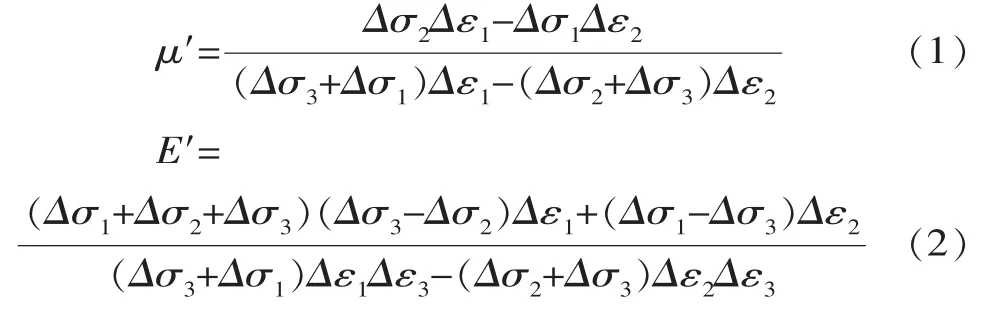
2 反演分析
2.1 區塊劃分
根據邊坡巖體的類型及強度、風化程度、剪切破碎帶、裂隙及斷層的走向和傾向、結構面的間距及連通率、力學參數、地下水情況等因素將邊坡劃分為不同的區塊,選取其中3個區塊 (2、3號和4號)進行二維、三維參數反演對比分析,其區塊劃分見圖1。
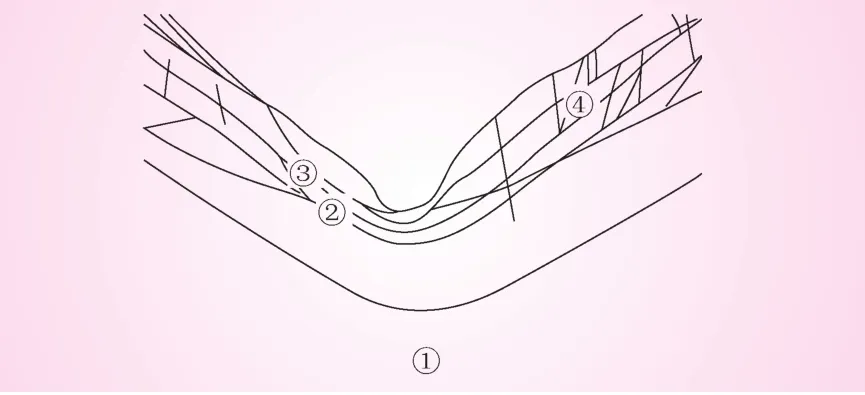
圖1 區塊劃分
(1)第2區塊:位于左岸弱下風化層內邊坡上,巖性主要為灰白色英安巖,巖體呈鑲嵌狀、塊裂狀結構,結構面發育,貫穿性結構面不多見,結構面延展差,多閉合,巖塊間嵌合力較好。
(2)第3區塊:位于左岸弱上風化層內邊坡上,巖性主要為灰白色英安巖,巖體呈鑲嵌狀、塊裂狀結構,結構面較發育。
(3)第4區塊:位于右岸弱上風化層內邊坡上,巖性主要為灰黑色英安巖,巖體呈鑲嵌狀結構,結構面較發育。
2.2 區塊二維參數反演
根據裂隙大小、性質、產狀等因素,將第2區塊分4級計算。其概化模型試件見圖2,初始參數見表1。
在ADINA中建立好宏觀力學參數分析模型后,設定材料參數進行計算,運行后處理文件,提取出節點數據,對節點應力、應變進行統計。最后,用巖體初始計算參數計算得到模擬試塊的宏觀變形參數。第2區塊巖體二維宏觀參數計算結果見表2。同理,第3、第4區塊巖體二維宏觀參數計算結果見表3、4。
2.3 區塊三維參數反演
三維有限元參數反分析也采用二維參數分析中各區域巖體與破碎帶的力學參數作為數值模擬的基本參數,將幾種不同的巖體和剪切破碎帶斷層等組合在一起構成計算試塊,并對其進行地質力學參數反分析,計算試塊的選定也與三維有限元模型結合起來考慮。進行三維模擬區塊斷層和結構面過程中,各級區塊大小以及結構面的分布和發育狀況均與二維模型保持一致,故此處不再贅述。

表1 第2區塊巖體的初始參數
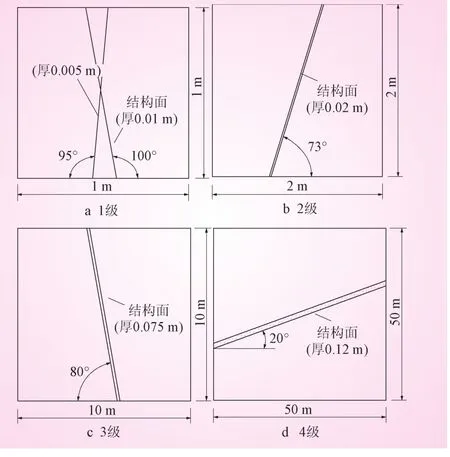
圖2 第2區塊計算概化二維模型
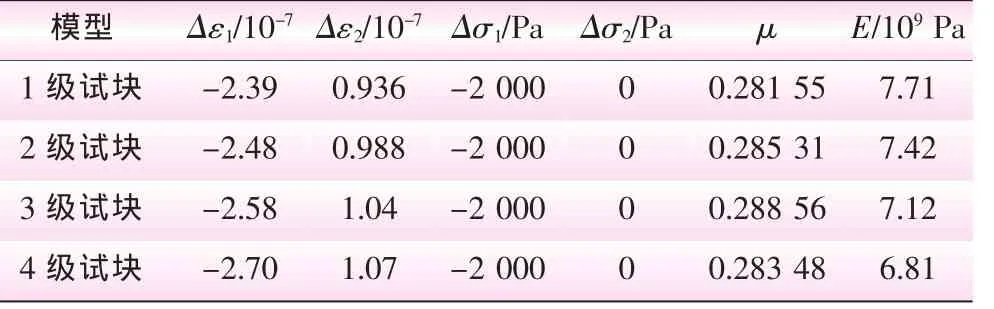
表2 第2區塊巖體的宏觀參數計算成果
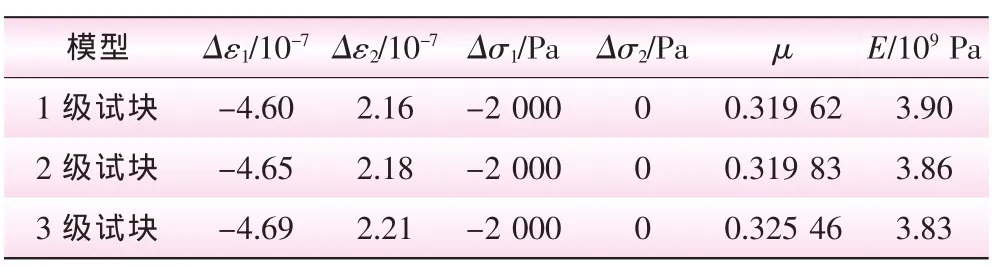
表3 第3區塊巖體的宏觀參數計算成果
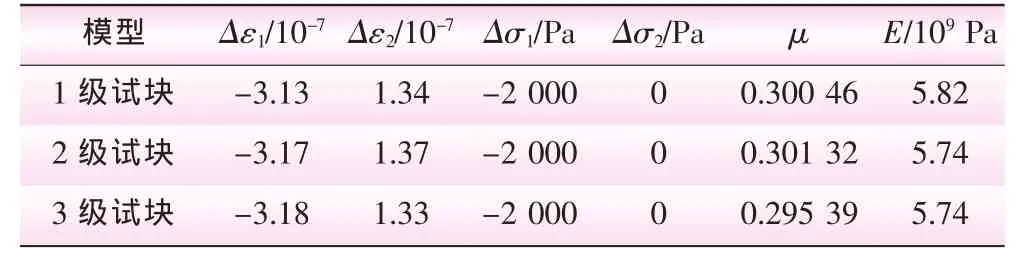
表4 第4區塊巖體的宏觀參數計算成果
根據裂隙大小,性質,產狀等因素,將第2區塊分為4級計算。其分級概化模型試件見圖3,初始參數見表1。在ADINA中建立好宏觀力學參數分析模型后,設定材料參數進行計算,運行后處理文件,提取出節點數據,對節點應力、應變進行統計,最后將統計得到的數據代入公式1、2,計算得到模擬試塊的宏觀變形參數,計算結果見表5。同理,第3、第4區塊巖體三維宏觀參數計算結果見表6、7。
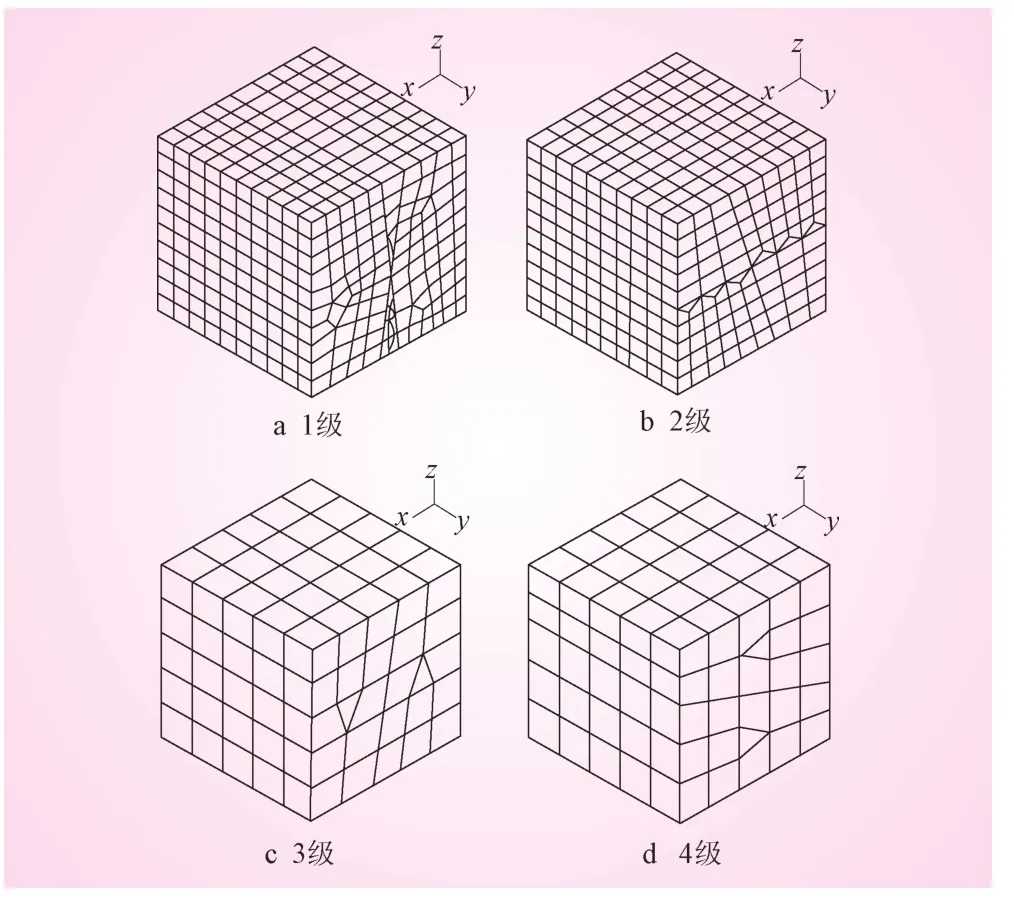
圖3 第2區塊分級計算概化三維模型
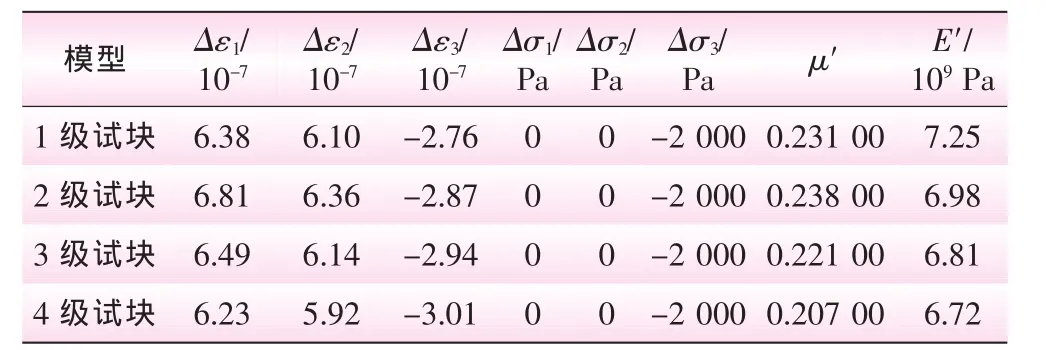
表5 第2區塊巖體三維宏觀參數計算成果
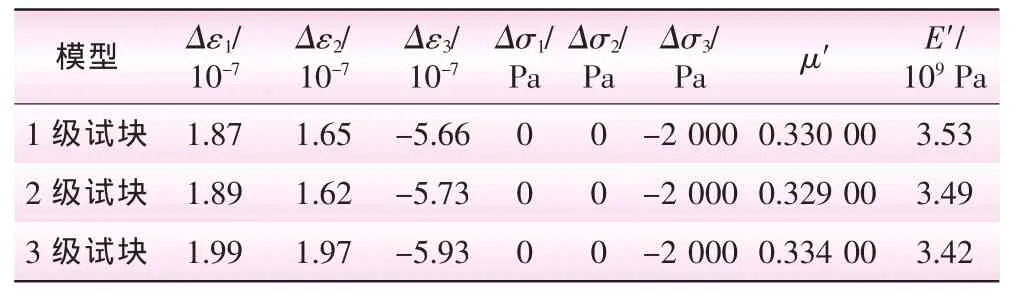
表6 第3區塊巖體三維宏觀參數計算成果
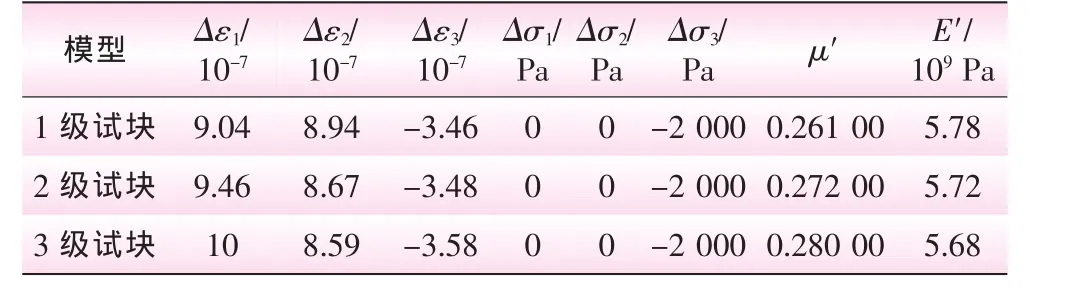
表7 第4區塊巖體三維宏觀參數計算成果
2.4 對比分析
3個區塊二維與三維模擬計算變形模量、泊松比對比見圖4。從圖4可以看出,二維和三維模擬裂隙對計算結果的影響程度幾乎一致。進行三維模擬時,變形模量的折減幅度比二維模擬略大,趨勢基本一致。同樣,泊松比的變化趨勢基本一致,均隨著計算級數的增大而增大,部分存在跳躍現象,其原因可能是:在三維模型中,由于結構面的存在,隨著頂面荷載的施加,另外2個側向臨空面中間會出現應變集中凸出,使該面的平均位移增加,即側向應變增大,故反求得出的泊松比隨之減小。
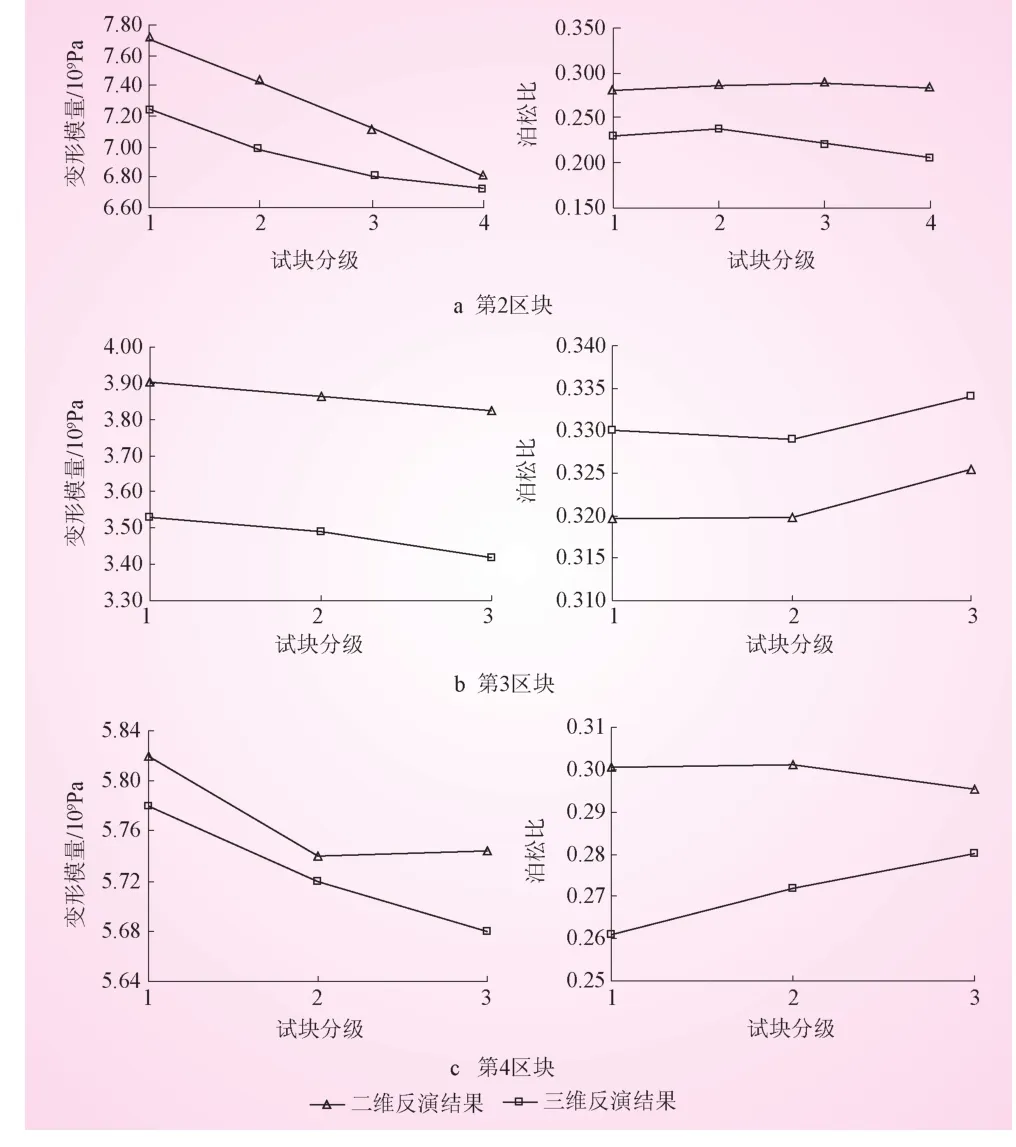
圖4 二維與三維計算變形模量、泊松比對比
3 結論
(1)本文采用分區分級計算試塊法解決了室內試驗對巖體參數評價的局限性和以經驗為主的方法提供巖體的力學參數對巖體參數選取的隨機性。
(2)綜合考慮巖體的結構類型與特點,將室內試驗成果運用到數值仿真分級模擬巖體的參數,由此得出的反演結果更具科學性。
(3)從二維到三維參數反演,精確地模擬巖體內部真實應力、應變狀態,大大提高了巖體參數分析的精確性。
(4)二維與三維的計算結果比較吻合,更加驗證了分區分級方法計算巖體力學參數的準確性和合理性。
[1]李建林,哈秋齡.三峽卸荷巖體宏觀力學參數三維數值模擬[J].武漢水利電力大學 (宜昌)學報,1997,9(3):1-6.
[2]楊學堂,哈秋船,張永興,等.裂隙巖體宏觀力學參數數值仿真模擬研究[J].水力發電,2004,30(7):14-16.
[3]周濟芳,李建林,劉杰,等.隔河巖水電站邊坡巖體宏觀力學參數的有限元反演分析[J].巖石力學與工程學報,2004,23(增1):4506-4508.
[4]帥春,何江達,謝紅強,等.某水電站樞紐區邊坡天然穩定性及巖體力學參數反演[J].成都理工大學學報:自然科學版,2009,36(5):511-515.
[5]李建林,王樂華,楊學堂,等.錦屏水電站壩廠區卸荷巖體力學參數研究[J].巖土力學,2004,25(增):17-20.
[6]駱世威,劉杰,肖蕾,等.西藏如美水電站裂隙巖體力學參數模擬反分析[J].人民長江,2012,43(10):84-87.
[7]李建林.巖石邊坡卸荷巖體宏觀參數研究[M].北京:中國建筑工業出版社,1996.
[8]張志強.非貫通裂隙巖體破壞細觀特征及其宏觀力學參數確定方法[D].西安:西安理工大學,2009.
[9]李建林.三峽工程永久船間陡高邊坡巖體宏觀力學參數研究[D].重慶:重慶建筑大學,1996.

