基于模糊神經網絡PID算法的電阻爐溫控系統

董愛華,李夢瑤

0 引言

電阻爐不僅在工業生產中非常廣泛的應用于冶金、機械、建材等行業[1][2]，而且在科研、教學中也有應用,它的溫度控制的優劣直接影響產品的品質[3]。

現階段，對電阻爐采用的主要控制方法是PID控制[4]，還有一些采用模糊控制和神經網絡控制。PID控制的控制參數一旦確定，便無法改變，對電阻爐這種時變的控制對象控制效果不是很好。當采用模糊算法時,模糊系統學習能力較差，模糊規則的建立和隸屬度函數的生成和調整較困難，模糊控制消除靜態誤差的能力較差,難以達到較高的控制精度[5]。當采用神經網絡控制時，不能利用現有的知識,無法引入人工經驗，不能依據已有的控制經驗來解決控制問題。

本文把三個控制算法融合起來，形成模糊神經網絡PID算法，兼有三種控制算法的優點，經仿真表明，該算法對電阻爐溫度的控制動靜態性能較好。

1 電阻爐模型

電阻爐溫控系統的簡圖如圖1所示：

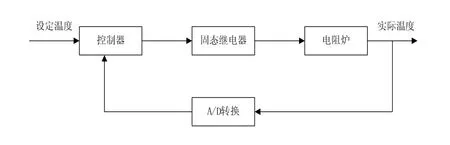
圖1 電阻爐溫控系統簡圖

通過改變一個周期內晶閘管的通斷時間，改變電阻爐的電壓，從而改變電阻爐的功率，使實際溫度跟隨設定溫度的變化而改變。

2 電阻爐模型

理論分析和實驗結果證明，電阻爐在階躍輸入影響下，具有非振蕩特性和自平衡能力，可用比例環節、一階慣性環節和一個延遲壞節來近似。其傳遞函數可以近似地表示成：

其中K—靜態增益，τ—純滯后時間，T—慣性時間常數。

3 模糊神經網絡PID控制器的設計

當|e(k)|＞ ε，(ε的大小決定著控制精度，ε越小，控制精度越高，程序越復雜；反之，ε越大，控制精度越低，程序越簡單)說明誤差較大，控制器按最大或最小輸出，具體到電阻爐溫度控制，即溫度誤差較大， 控制器以最大或最小輸出，電阻爐全功率或功率為零，也就是控制電阻爐電壓為最大或零。當|e(k)|<ε,系統采用模糊神經網絡PID控制。在實際應用中，根據不同控制精度的要求，多次調試，選擇合適的ε。

本文提出的模糊神經網絡PID控制器的結構，如圖2所示：

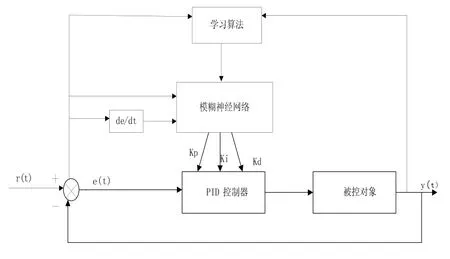
圖2 模糊神經網絡PID控制器的結構圖

模糊神經網絡PID主要有兩個部分組成（1）傳統的PID控制器。這是控制器的核心，PID控制器對被控對象直接進行閉環控制，模糊神經網絡主要作用是實時調節PID控制器的參數,從而達到最好的控制效果。它的最大特點是控制參數Kp、Ki、Kd是實時改變的。（2）模糊神經網絡FNN，根據系統的實時運行狀態，即根據誤差和誤差變化率來調節PID控制器的參數，使控制指標達到最優[6]。

本文中的PID控制并不是簡單的比例、微分和積分的“線性組合”關系[7]，若想取得較好的控制效果，必須使比例、積分和微分3種控制作用達到最佳的組合。模糊神經網絡的主要任務就是利用模糊神經網絡理論建立誤差e(k)、誤差變化率ec(k)和PID控制器的3個參數Kp、Ki、Kd的關系。

如公式（2）

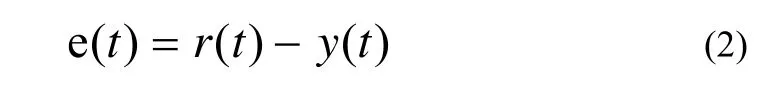
e(t)—t時刻的采樣誤差;y(t)—被控對象t時刻的實際輸出：r(t)—t時刻的設定輸出：t—采樣時間。

3.1 PID控制原理

控制器采用的最多的是PID控制，PID控制是一種線性控制方法，原理框圖如圖3所示。其位置式控制規律，如圖3所示：

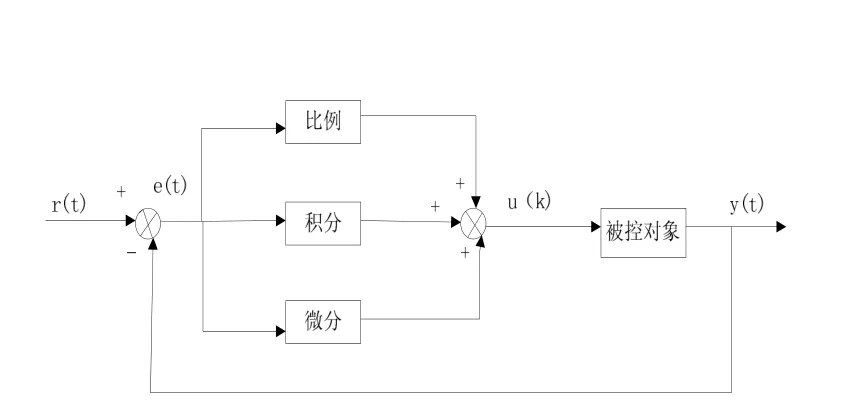
圖3 PID控制系統原理框圖

如公式（3）

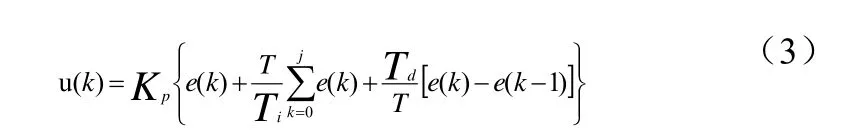
其中u(k)—第k次采樣時刻控制器輸出的控制量；Kp—比例系數;Ti—積分時間常數；Td—微分時間常數；T采樣周期；Ki=Kp/Ti為積分系數，Kd=KpTd為微分系數，e(k)和e(k-1)分別是第k和k-1次采樣時刻輸入誤差值。

3.2 模糊神經網絡的結構和設計

模糊神經網絡（FNN）將神經網絡的學習能力引入到模糊系統中，將模糊系統的模糊化處理、模糊推理通過神經網絡來表示[8]，一般分為四層：1 輸入層；2 模糊化層；3 模糊推理層；4 輸出層。它的結構圖，如圖4所示：

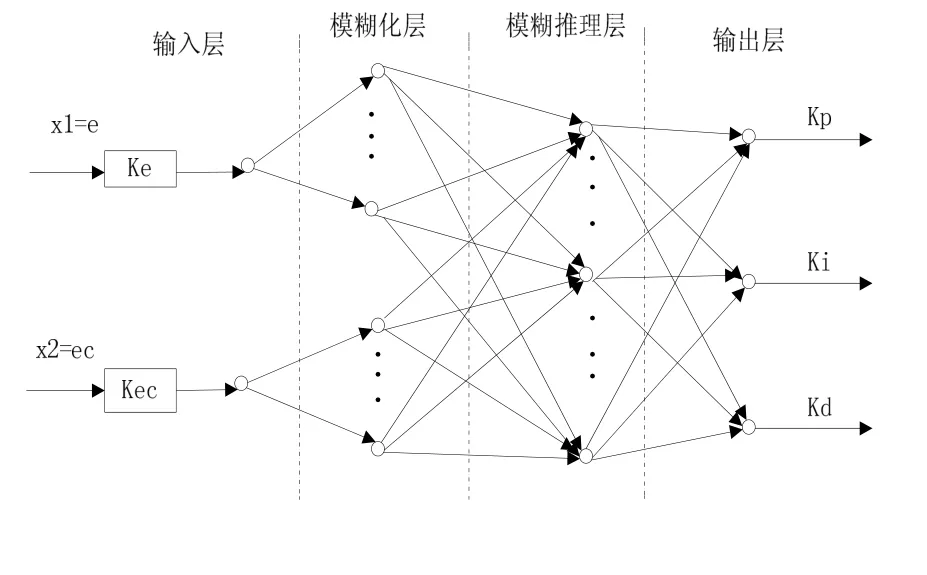
圖4 模糊神經網絡結構圖

輸入層與模糊化層、模糊化層與模糊推理層之間的連接權值均為l，只有模糊推理層與輸出層之間的權值需要調整。

本文中的模糊神經網絡是2-6-9-3結構，兩個輸入神經元，3個輸出神經元分別對應PID控制器的3個參數Kp、Ki、Kd。

模糊神經網絡各層的輸入輸出關系如下：

第1層（輸入層）：作用將輸入量導入網絡，如公式（4）

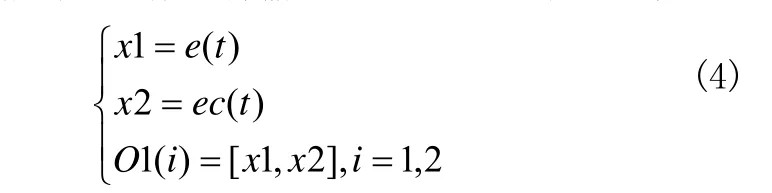
第2層（模糊化層）：將輸入變量模糊化，計算輸出各輸入變量屬于各語言變量的隸屬度函數。本層有6個節點，分別對應誤差和誤差變化率的語言變量:B(大),M（中）,S（小）。語言變量的個數的選擇和系統的復雜程度和控制精度的要求有關。控制精度要求高，系統復雜，選擇的語言變量個數就要多，如公式（5）

模糊化層采用高斯型函數作為隸屬函數,cij和bij分別是隸屬函數的中心值和寬度。

第3層（模糊推理層）：

由輸入變量個數N=2，每個變量的模糊子集數為M=7，根據y=MN,可得此層的節點數m=9[9]。

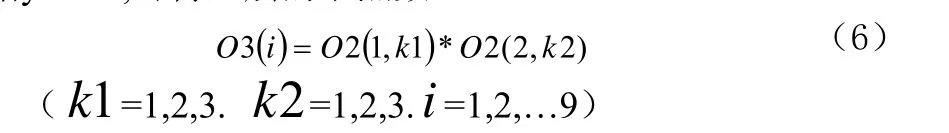
第4層（輸出層）：

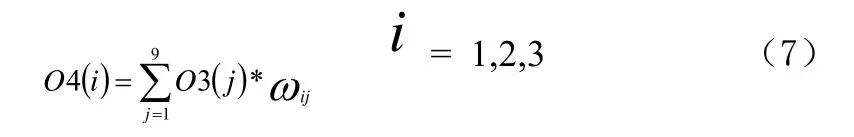
ωij是模糊推理層與輸出層之間的權值。三個輸出神經元的輸出為PID控制器的三個參數Kp、Ki、Kd。

3.3 模糊神經網絡的學習算法

系統的目標函數：

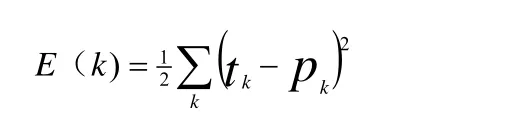
tk第k個神經元的期望輸出， pk第k個神經元的實際輸出。

模糊神經網絡的高斯函數的中心cij和寬度cij，及模糊推理層與輸出層之間的權值ωij采用BP的梯度下降法。

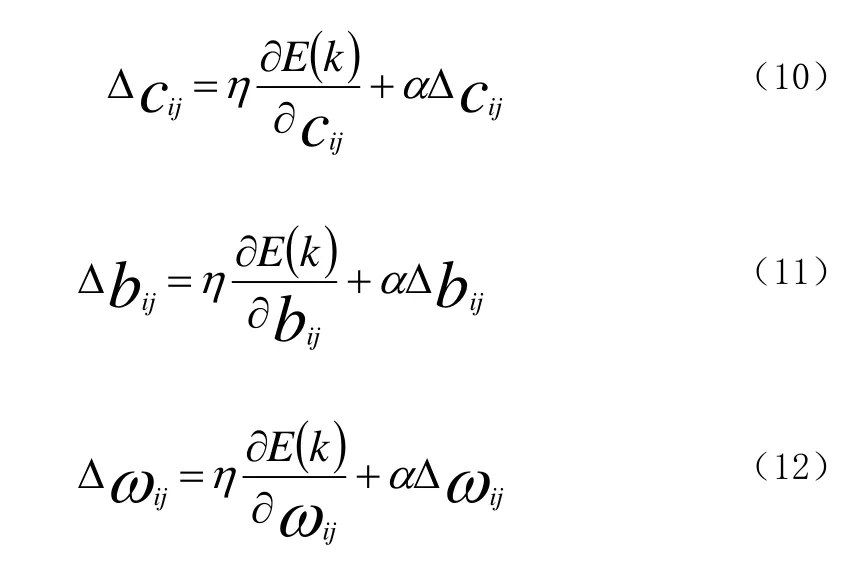
η為學習速率，α為慣性系數。

4 仿真結果與分析

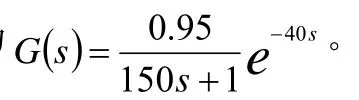
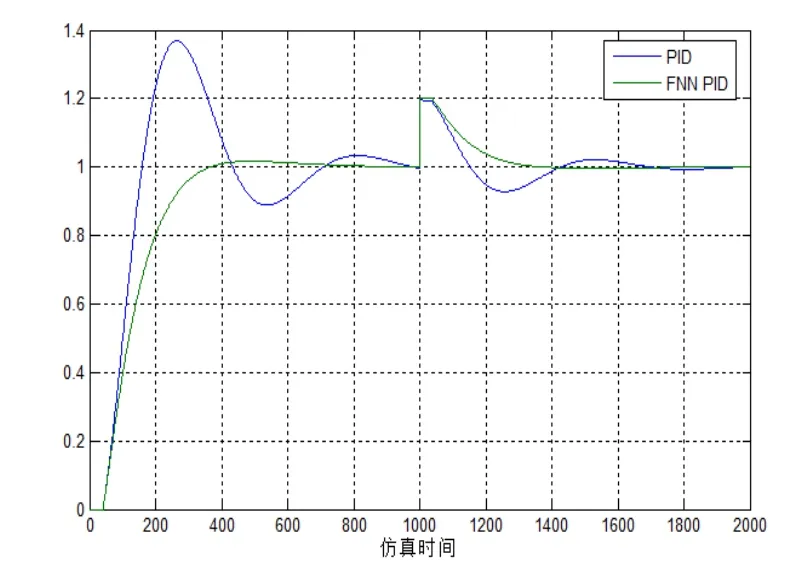
圖5 仿真曲線圖

從仿真曲線可知，模糊神經網絡PID（FNN PID）和PID比較：模糊神經網絡PID上升速度快，超調量基本為零，在加入外部擾動時，能快速的調節到穩定。

[1]邢偉.電阻爐智能模糊控制系統的研制[D].杭州: 浙江理工大學,2008.

[2]謝錚輝,馬有良,鄧琥等.基于PID的電阻爐爐溫控制系統[J].化工自動化及儀表,2011,38(8):931-933

[3]孫凱,李元科.電阻爐溫度控制系統[J].傳感器技術,2003,22(2):50-52.

[4]馬雪峰,田躍輝，李玲莉.一種改進PID控制算法在電阻爐溫度控制系統中的應用[J].船海工程,2009,38(2):68-70.

[5]李英順 ,倫淑嫻.模糊PID溫度測控儀[J].儀表技術與傳感器,2003,(1):20-22

[6]張妤.基于知識的模糊神經網絡PID控制器的研究[D].哈爾濱：哈爾濱理工大學，2006.

[7]王彥，鄧勇，王超.基于改進粒子群算法的模糊神經網絡PID控制器設計[J].控制工程，2012,19（5）：761-764.

[8]劉敏，馬軍爽.模糊RBF 神經網絡在鍋爐水位控制中的應用[J].微計算機信息, 2006 ,22 ,（9-1 ）：56-58.

[9]劉莉，張彥敏.基于改進遺傳算法的FNN PID控制器在溫度控制系統中的應用[J].工業控制計算機，2009，22（3）：63-65.