基于ANSYS Workbench的電主軸系統靜態特性分析
沈山山,鐘建琳,米 潔,陳秀梅
SHEN Shan-shan,ZHONG Jian-lin,MI Jie,CHEN Xiu-mei
(北京信息科技大學 機電學院,北京 100192)
0 引言
高速切削能夠提高生產效率、保障表面加工質量,是先進制造技術的重要研究內容。高速數控機床必須具有良好的靜態特性,才能保證機床的可靠性以及加工精度,從而有效地實現高速切削。然而,電主軸系統是高速數控機床的關鍵核心部件,其靜剛度會直接影響機床的加工性能。因此,在設計機床階段必須做好電主軸系統的靜態特性研究。
1 電主軸系統的主要結構
該主軸系統的設計要求達到較高的靜剛度,從而能應用于高轉速的機床。電主軸系統的結構如圖1所示。主軸的外徑為180mm,主軸內徑為50mm。主軸的電機位置放在前后軸承之間。主軸的前后軸承型號分別為32036-X-P5和NN3019ASK-MSP。其中前軸承成對使用,定位預緊,從而限制主軸的軸向位移,起到固定作用。并且,前軸承在背對背安裝的方式下可以使兩個軸承的接觸點之間存在的距離增大,從而增大主軸的抗彎力矩,最終達到提高主軸剛度的作用。因為主軸受熱后會向后延伸,為保證主軸的精度,后軸承采用的雙聯滾子軸承主要起到浮動支承作用,這種支承形式能夠適應大轉速、高負載、高剛度的要求。
2 電主軸系統有限元模型建立
2.1 模型簡化

圖1 主軸系統結構圖
主軸單元具有多支承、承受載荷種類多、高速旋轉等特點,所以主軸單元屬于復雜的超靜定梁結構,不便于計算,因此在建立有限元模型時需要忽略主軸單元在軸線上的扭轉振動[1]。在結構方面,由于電主軸系統是復雜的裝配體,并且有大量螺紋、倒角等細小結構,因此為減小計算規模需要將模型進行簡化。考慮到以上原因,對電主軸系統模型提出以下簡化方案:
1)將軸承簡化為彈性支承,在ANSYS Workbench中建立有限元模型時,用彈簧代替彈性支承單元。
2)將電機定子等效為同密度主軸箱材料,將電機轉子以及過盈襯套簡化為主軸材料,在建立有限元模型時,將以上設定為同種材料的零部件的結合面設置為綁定狀態,使電機的定子與轉子分別成為主軸箱與主軸的附加分布質量;
3)電主軸系統中有些小零件的作用僅僅是封閉主軸系統,并不起到傳遞力的作用,因此,為簡化模型需要將其忽略;
4)主軸箱上存在多個螺栓連接孔、定位孔等細小結構,這些結構對結構影響很小,為簡化計算將其刪除;
5)由于電主軸系統是對稱結構,為了減少計算量,同時也便于在電主軸系統結構內部施加約束與載荷,使用對稱特征(Symmetry)來創建對稱模型的簡化模型,只保留模型的一半進行分析[2]。并且,為保證分析結果的正確性,在簡化模型的對稱面上施加無摩擦約束(Frictionless Support),來模擬對稱邊界約束。
2.2 簡化軸承
在模型簡化過程中,用彈簧代替彈性支承單元。在徑向方向上,前后軸承的簡化方式相同,每個軸承都簡化為4個均布在主軸上的彈簧單元,彈簧的兩端分別與主軸和主軸箱固結,用來傳遞徑向力。在軸向方向上,由于后軸承只是起浮動支承的作用,故可忽略其軸向剛度。而前軸承是圓錐滾子軸承成對背對背安裝,是主軸與主軸箱之間傳遞軸向力的關鍵部件,故將每個軸承簡化為4個均布在主軸周圍的軸向彈簧,用來傳遞軸向力。
非線性彈性變形是主軸軸承的典型特點,這使得主軸軸承的剛度隨軸承載荷而變化,并不是一個定值。軸承轉速越高,離心力會使剛度降低,但同時軸承的發熱量會給剛度一定補償,因此在簡化模型時,可以將軸承的剛度設為定值[3]。
在電主軸系統中前軸承需要定位預緊,因此彈簧單元的剛度應簡化為定位預緊情況下的軸承剛度。圓錐滾子軸承徑向定位預緊剛度計算方法為[4]:
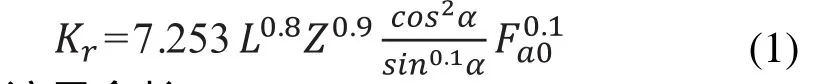
L—滾子全長,mm
Z—每列滾動體滾子數
α—接觸角
Fα0—預緊力
圓錐滾子軸承軸向定位預緊剛度計算方法為:
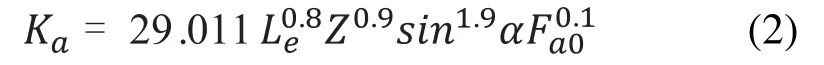
Le—圓錐滾子軸承滾子有效接觸長度
圓柱滾子軸承,其徑向剛度的計算方法為[5]:
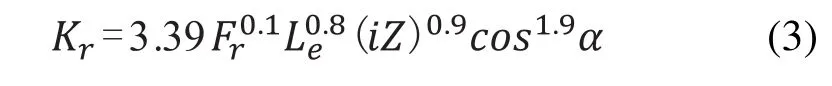
Fr—徑向載荷
i—滾動體的列數
以上計算方法中所需參數通過查閱軸承應用手冊而獲得[6]。計算得到前軸承的徑向剛度為1771N/μm,軸向剛度為509N/μm,后軸承的徑向剛度為1327N/μ m。
2.3 材料屬性以及邊界條件
在ANSYS Workbench中對簡化后的模型進行材料屬性設置。主軸箱材料的密度為7340kg/m3,彈性模量為1.3×1011Pa,泊松比為0.25;主軸材料的密度為7830kg/m3,彈性模量為1.3×1011Pa,泊松比為0.27。

圖2 電主軸系統有限元模型

圖3 電主軸變形
有限元模型的邊界條件主要指施加在模型上的約束和載荷,確定模型的約束邊界是有限元分析的基礎。電主軸系統中關鍵的約束條件主要有絲杠裝配孔以及主軸箱與導軌結合面處的約束。主軸箱在絲杠的作用下沿Y軸方向運動,故將絲杠裝配孔的邊界條件簡化為Y方向的位移約束。主軸箱與導軌的連接平面設定為剛性平面,故將其設置為固定約束。
電主軸系統的有限元模型如圖2所示。
3 電主軸系統的靜態特性分析求解
高速主軸靜態分析的目的是計算主軸系統的靜剛度。主軸的靜剛度包括主軸的軸向剛度和彎曲剛度,彎曲剛度指在徑向力作用下使主軸產生單位徑向位移所需的力;軸向剛度是指在軸向力作用下使主軸產生單位軸向位移所需的力。一般所說的主軸剛度主要指彎曲剛度[7]。
在ANSYS Workbench的Mechanical模塊中于主軸的前端施加1000N的徑向載荷,然后對有限元模型進行運算,如圖3、圖4所示為經過分析得到的電主軸和主軸箱的靜態變形結果。

圖4 主軸箱變形
靜剛度的計算方法為:

由圖靜態變形結果可知,主軸的最大位移為Dmax=0.54227 μ m,則電主軸的靜剛度為1844N/μm。主軸箱的最大位移Dmax=0.39847μm,則主軸箱的靜剛度為2509N/μm。該電主軸設計要求的靜剛度為1795N/μm,上述結果說明該電主軸符合靜剛度要求。為驗證本文有限元模型建立的準確性,將計算結果與同類主軸系統的剛度進行比較。太原第一機床廠的CNC30數控機床的主軸徑向剛度為551.42/μ m,其前軸承的內徑為,經驗證,軸承內徑與主軸徑向剛度的關系滿足圖5所示關系曲線[8]。本文中主軸的前軸承內徑大小為180mm,計算所得主軸的徑向剛度為1844N/μm,該結果同樣符合圖5所示曲線。綜上,說明該主軸系統的有限元模型建立方法正確有效。
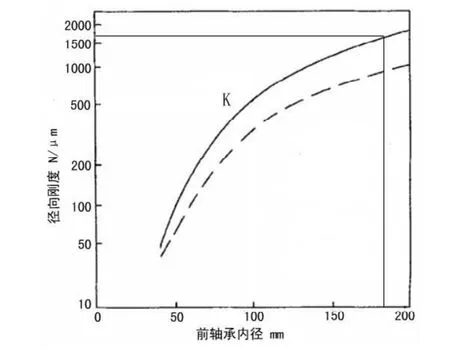
圖5 前軸承內徑和徑向剛度曲線圖
4 結論
電主軸系統是高速機床的關鍵部件,其靜剛度直接影響著機床的加工精度。在設計主軸的過程中對其進行靜態特性分析至關重要,通過有限元分析可以驗證主軸的靜剛度是否滿足設計要求,若未達到要求,可以通過改進主軸跨距、軸承預緊力等方式來改善主軸的靜態特性。
本文運用有限元分析軟件ANSYS Workbench對電主軸系統進行了有限元建模,進而研究了主軸系統的靜剛度。本文建立的電主軸系統的有限元模型的準確性較高,為機床的動態特性分析打下堅實的基礎,該建模與分析方法同樣能夠應用到機床其他關鍵部件的靜、動態特性分析中。
[1] 王新新,廖敏,吳軍強.基于ANSYS的加工中心電主軸靜態性能分析[J].機械設計與制造,2012(1):201-203.
[2] 李兵,何正嘉,陳雪峰.ANSYS Workbench設計、仿真與優化[M].北京:清華大學出版社,2008.
[3] 劉玉.高速機床主軸單元的動態特性分析及結構優化[D].青海:青海大學,2012.
[4] 李為民.圓錐滾子軸承軸向定位預緊剛度計算[J].軸承,2004(5):1-3.
[5] 張海杰.軸承對高速電主軸靜動剛度影響的研究[D].蘭州:蘭州理工大學,2011.
[6] 戴曙.機床滾動軸承應用手冊[K].北京:機械工業出版社,1993.
[7] 宋春明,趙寧,張士勇,張政武.高速電主軸結構參數優化設計[J].組合機床與自動化加工技術,2007,(7):79-81.
[8] 楊美英.數控機床主軸組件設計及剛度計算[J].機械工程與自動化.2004,4(2):71-73.

