鋼軌軌腰圓孔集中應力變形的理論與實驗研究

王宏偉，王春明，于冠東

WANG Hong-wei,WANG Chun-ming,YU Guan-Dong

（包頭鋼鐵職業(yè)技術學院，包頭 014010）

0 引言

鐵路鋼軌承載著火車運行的主要任務，同時也是感測鐵路信號的重要載體。為了實現對列車的自動控制，必須實時監(jiān)測其運行狀態(tài)。鋼軌在列車經過的瞬間，一定會在電、磁、聲等各方面產生變化[1]。同時，列車從鋼軌上經過，鋼軌在承受巨大載荷的同時，也一定會產生一個相當復雜的變形。從原理來看，作為感測對象，鋼軌承載變形在以上提到的諸多物理量變化中應該是最直觀可靠的，不易造成其他信號的擾亂。但是，經大量理論、實驗研究證明，列車經過輪軌的瞬間，其變形量非常微小[2]，因此感測鐵軌變形非常困難。經過實驗數據比對，我們另辟蹊徑，設計了一套方案：由于應力集中會使承載變形加劇，從而達到易于感測、準確感測這一物理量的目的，所以在鋼軌本體設計產生應力集中的結構。

1 人為增加集中應力結構的方案選取

一般來說，實際的構件，在有圓孔、缺口等處，由于其橫截面的形狀發(fā)生突變，造成局部地方發(fā)生非常大的應力，這就是應力集中現象。應力集中會造成變形量急劇增大，但同時一些應力集中會使鋼軌產生裂紋，長期會失效，嚴重降低強度。所以在分析了多種人為增加應力集中結構的方案后，得出結論：在鋼軌軌腰處鉆孔是最佳選擇。主要原因有兩點：

1）在鋪設鋼軌時要有必需的節(jié)節(jié)連接，所以鋼軌本身在制造過程中就有鉆孔的結構設計。這就簡化了安裝成本，利于檢測元件的普及。

2）結合圓孔設計的傳感器在結構上容易給予相應的補償措施，最大限度的彌補由應力集中削弱的鋼軌強度。

因此，在鋼軌的軌腰處，鉆一個直徑約30mm的孔(如圖1所示)。在火車載荷作用下，孔的周圍會產生應力集中。通過人為增加應力集中變形，使感測對象更易于測量。

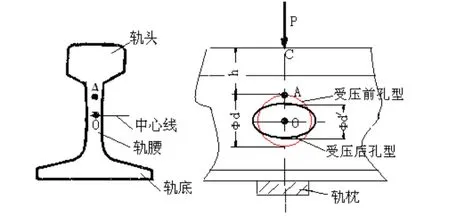
圖1 鋼軌上孔的應力集中變形示意圖

2 選取由于應力集中產生變形的最佳測試對象

對于一個承載后的鋼軌，其軌腰處孔變形量最大的位置就是我們要找的監(jiān)測點，即最佳測試對象。

2.1 建立力學模型

為了容易展開研究，問題簡單化，首先建立力學模型。把鋼軌當做平面梁，并且其上受到集中載荷的壓力。鎖定研究對象為枕木上端的一段鋼軌。此處，有兩點簡化，使之成為平面問題：

1）鋼軌橫截面由原來的變截面看成等厚平板，厚度為b（力的傳遞性）；

2）假定鋼軌承受作用力（F）在寬度方向上是均布的，則可得載荷（P）如下式：

2.2 集中應力產生的最大應力σmax和測試點的確定

根據以上力學模型的建立，我們將問題簡化為有一個圓孔的無限扳承受均勻壓力的情況（如圖2），圓孔半徑為r。在圓孔周圍將產生應力集中現象，其各點應力分布狀態(tài)可用以圓孔中心O為原點的極坐標r、θ表示如下[3]：

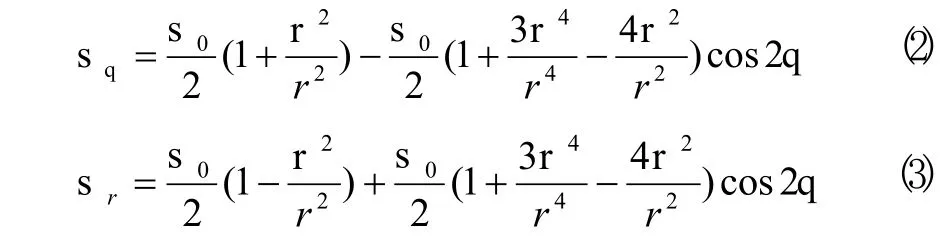
其中 σ0為基準應力。

對式(2)和式(3)求導，得到應力的最大值將出現在點A(r=r q=p/ 2,3p/2)，最大值為：

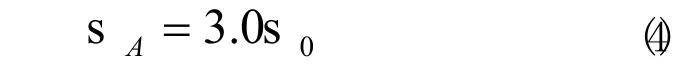
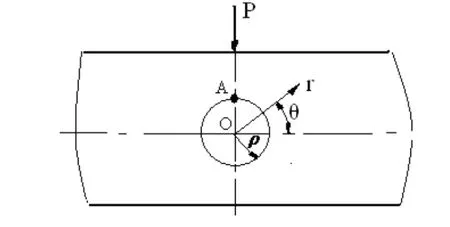
圖2 力學模型

可見，載荷作用線剛好經過枕木正上方時，孔在載荷作用線上的直徑變化量是最大變形量。由此，孔的圓度將發(fā)生如圖1的變化，由圓形變?yōu)闄E圓形，可見其直徑差 (Δd)max=f d?fd′是最佳測試對象。以下將從理論計算和實驗研究兩方面來具體確定這個變形量。

3 理論計算

3.1 基準應力σ0的確定

根據基準應力的選取方法[3]： 在沒有應力集中的基準應力分布已經不是均勻分布的情況下，要選取假定沒有應力集中因素時可能產生的應力為基準應力。

在鋼軌枕木上端的一段，其軌腰處的應力是一個接觸應力，分布是不均勻的[2]。其受力曲線呈現正態(tài)分布，即在軌腰的載荷作用力線上最大，并以其為中心，在軌腰長度方向上，分別向兩邊對稱快速的正態(tài)衰減。在應力集中系數一定的情況下，最大應力點也就是在標準應力最大的地方。即在沒有應力集中因素時可能產生的最大的應力點位置。因此，我們將載荷作用線上或者說孔中心線上與孔上邊緣交點A點（見圖1）在未鉆孔之前的應力作為應力集中分析的基準應力。則[4]：

式中：P為作用于鋼軌上的載荷；

h為A點與載荷P作用點C的距離。

3.2 理論計算推導

在未鉆孔前，A點的垂直位移量計算：

A點在載荷作用線上徑向位移（即垂直位移量）u取得最大值（水平方向位移量v(θ=0)=0為）[2]：

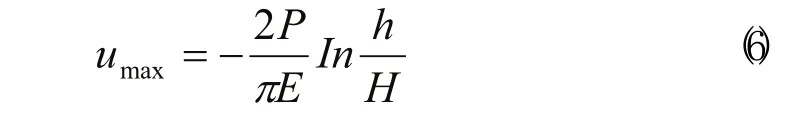
式中：E為材料的彈性模量，對于鋼軌材料，E=210GPa；

H為假設位移為0的點M距載荷作用點C的垂直距離。在此為鋼軌全高。

那么，由于集中應力的影響，圓孔在載荷作用線上，其直徑的最大變形量計算公式如下[5]：

b為應力變形系數，即相同的載荷作用下，同一點在有應力集中的位移量是無應力集中的位移量的倍數。這個值也說明了采取應力集中使感測目標實際擴大的倍數。也是本論題的研究意義在數值上的具體體現。

對于在實驗中，我們應用的50鋼軌，其結構尺寸如圖3所示，將各數據帶入式9，可得：b50=3.848。如果是60鋼，同樣根據其結構尺寸，計算出b60＝3.785。可見，隨著鋼軌重型尺寸的增大，其應力集中產生的相對變形量也越小。

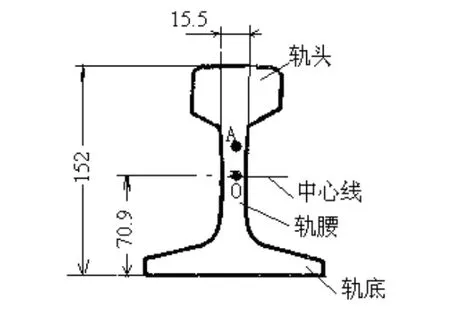
圖3 50鋼軌結構尺寸圖

3.3 理論計算值

下面，以50鋼軌為例，計算其在各載荷作用下，軌腰處直徑為?30mm的孔的直徑最大變形量(Δd)max（將各尺寸帶入式(8)）。結果見表1計算形變量一列。

表1 孔變形量計算值和測量值對比表

經力學校核：檢測靈敏度約為 287赫茲/1微米。

4 實驗測量

由于應力集中問題非常復雜，為簡化問題提出太多假設，所以理論計算值的準確度也會大打折扣。所以，在理論計算的基礎上做實驗測量驗證，是非常有必要的。下面對軌腰處直徑為?30mm孔的最大變形量 (Δd)max進行真實的實驗測量。

4.1 自制測量儀器的結構

經理論計算所得，檢測目標 (Δd)max值雖然有所放大，但仍是微米級的量，所以我們選擇電容式傳感器作為結構設計的基礎[6]，并自制了精確的測量裝置，可以準確地感測檢測對象。具體電容式測量裝置的結構圖如圖4所示。

儀器由電容上極板組合體、下極板組合體、屏蔽外殼及端蓋組成。由于感測信號極其微弱，極易受到來自外界信號的干擾，所以，設計雙層的全封閉屏蔽外殼。將與電容下極板相連的下極板組合體至于其中，并與外殼內層粘接形成一體。將帶有電容上極板的上極板組合體插入已經粘接了下極板組合體的外殼內，使電容上下極板間形成一個固定的微距離，同時將屏蔽外殼上平面封閉，最后蓋上后端蓋，形成全封閉結構（如圖5所示）。

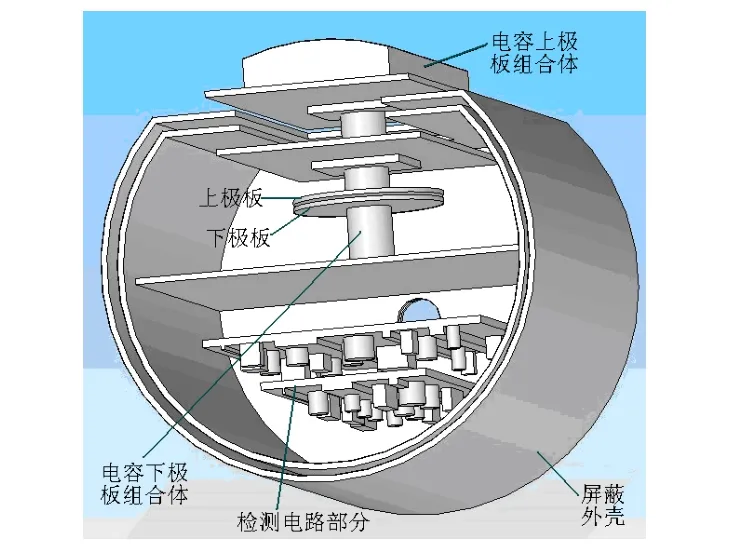
圖4 測量裝置裝配圖

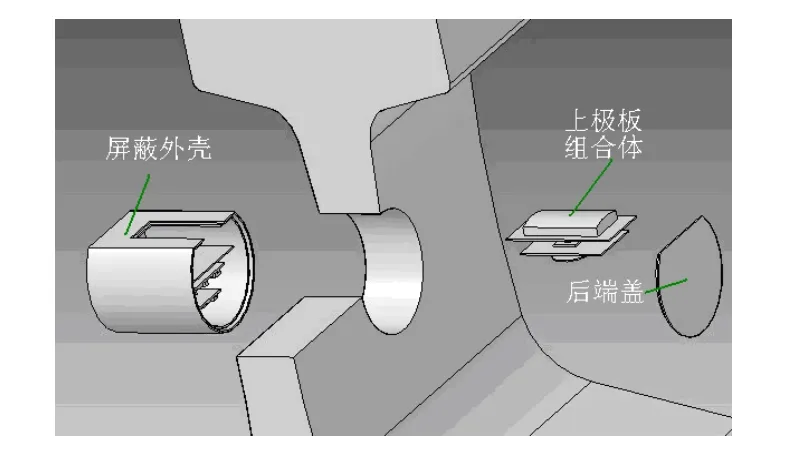
圖5 測量裝置組裝過程

4.2 測量過程及工作原理

測量前，首先將上極板組合體對正粘結在圖1中相當于A點的位置，然后將已經粘接了下極板組合體的外殼與上極板組合體裝配好，并將其與圓孔下部粘接固定好。

測量時，在事先標好的圓孔中心線上逐步施加載荷P(如圖1所示)。鋼軌圓孔受到載荷P的作用，其圓度發(fā)生變形，孔在載荷作用線上圓孔的上下面由于分別與電容上下極板粘接固定，所以會分別帶動上下極板運動，使圓孔直徑的最大變形量1：1的反應為電容兩極板間距離的改變。通過與之相連的檢測電路，就可檢測到圓孔直徑的最大變形量。

4.3 測量結果

試驗中以50鋼軌為例，測量其在各載荷作用下，軌腰處直徑為?30mm的孔的直徑最大變形量(Δd)max。結果見表1實驗檢測折合形變量（微米）一列。

5 結論

通過表1對理論計算和實驗測量兩方面的數據比對，可以看到，鉆孔后的鋼軌應力集中變形遠大于沒有鉆孔前該處的變形量，突破了感測變形量困難的瓶頸問題。為我們將鋼軌的承載變形量作為感測對象設計列車信號控制元件的思路提供了有力的依據，并為后期感測控制元件的具體結構設計在數據上提供了保障。

[1] 陳杰,黃鴻.傳感器與檢測技術[M].北京∶高等教育出版社.2002.

[2] 王宏偉,王春明,于冠東.基于感測控制的鋼軌承載變形實驗研究[J].制造業(yè)自動化,2012,34(7)∶147-150.

[3] 西田正孝.應力集中[M].北京∶機械工業(yè)出版社.1986.

[4] 劉鴻文.高等材料力學[M].北京∶高等教育出版社.2002.

[5] 黃炎.局部應力及其應用[M].北京∶機械工業(yè)出版社.1986.

[6] 王宏偉,王春明,于冠東.基于自動控制的微變形感應系統(tǒng)研究[J].包鋼科技.2012,38(3)∶55-57.