基于EC-RBF學(xué)習(xí)算法的機械臂運動學(xué)逆解研究

張 翠，楊劍鋒，張 峰

（蘭州交通大學(xué)，蘭州 730070）

0 引言

機械臂運動學(xué)逆問題指給定機械臂末端執(zhí)行器的空間位姿，求解為達到該位姿而所需的關(guān)節(jié)變量[1]，是正問題的反向求解過程。現(xiàn)有求解方法主要有代數(shù)法、幾何法、迭代法以及基于神經(jīng)網(wǎng)絡(luò)的求解方法[2～6]等。利用神經(jīng)網(wǎng)絡(luò)來進行機械臂逆運動學(xué)求解，以滿足控制器設(shè)計中的精度要求及解決多值性問題[6]，成為一種極為有效的途徑。

本文采用熵聚類學(xué)習(xí)算法來訓(xùn)練RBF神經(jīng)網(wǎng)絡(luò)（En tropy Clustering RBF，EC-RBF），對機械臂運動學(xué)逆問題進行辨識求解，在滿足一定精度要求的同時加速網(wǎng)絡(luò)訓(xùn)練過程，為下一步控制器設(shè)計問題中的實時性問題提供可能。

1 機械臂運動學(xué)分析

本文研究對象為自主研發(fā)的具有四個自由度的教學(xué)用關(guān)節(jié)型機械臂，由三個旋轉(zhuǎn)關(guān)節(jié)以及一個自由旋轉(zhuǎn)底座構(gòu)成，實現(xiàn)在空間內(nèi)運動。分析其運動學(xué)問題，采用Denavit-Hartenberg(D-H)方法建立其運動學(xué)方程，根據(jù)機械臂實際參數(shù)計算相鄰關(guān)節(jié)變換矩陣，其中 為連桿扭角， 為連桿長度、 為連桿距離，且均為常量分； 為關(guān)節(jié)變量。機械臂末端執(zhí)行器相對于基坐標系的總變換矩陣為：

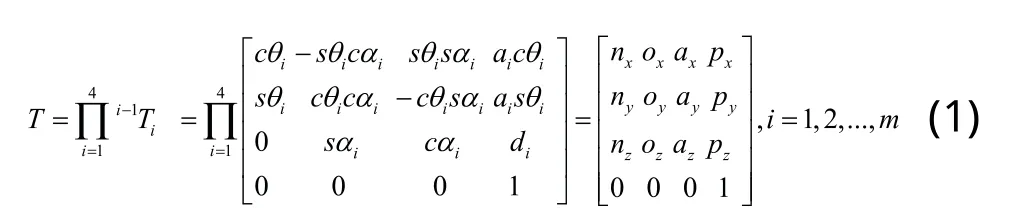
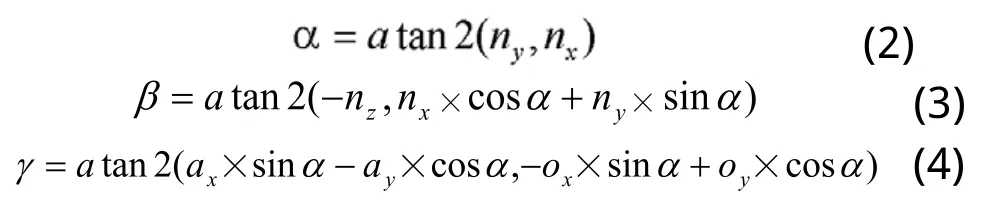
2 EC-RBF神經(jīng)網(wǎng)絡(luò)算法

EC-RBF神經(jīng)網(wǎng)絡(luò)算法，先通過熵聚類算法確定聚類中心初值和聚類數(shù)目，再利用K-m eans算法進一步調(diào)整和修改RBF函數(shù)的中心值和寬度。熵聚類算法實現(xiàn)的步驟大體分為4步[7,8]，在文獻中有詳述，這里不再贅述。本文中EC-RBF神經(jīng)網(wǎng)絡(luò)算法具體步驟如下：

4)判斷所有的訓(xùn)練樣本且中心分布是否不再變化。在實際應(yīng)用過程中，只要中心的變化(設(shè)定值），可認為中心不再有任何變化。否則，轉(zhuǎn) 2)繼續(xù)。

5)寬度半徑 等于每個聚類中心與屬于該類的樣本之間的平均距離，即：

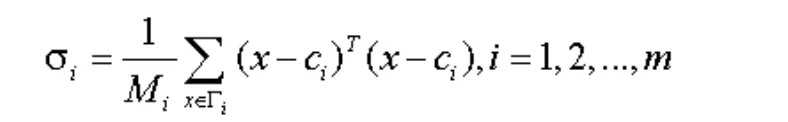
6)輸出權(quán)值 采用線性的偽逆算法來調(diào)整，R為網(wǎng)絡(luò)隱節(jié)點輸出， 為網(wǎng)絡(luò)期望輸出，即

由于省去了網(wǎng)絡(luò)學(xué)習(xí)算法過程中尋找初值和聚類數(shù)的迭代計算量，因而能夠保證RBF神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)的快速性。

3 機械臂運動學(xué)逆解的EC-RBF實現(xiàn)

2）訓(xùn)練EC-RBF神經(jīng)網(wǎng)絡(luò)

選取1500組數(shù)據(jù)，采用EC-RBF算法來訓(xùn)練神經(jīng)網(wǎng)絡(luò)。經(jīng)過多次試驗，最優(yōu)參數(shù)取表1為從網(wǎng)絡(luò)輸出的逆解結(jié)果中截取的關(guān)節(jié)角的部分數(shù)據(jù)，并與目標值比較。

表1 關(guān)節(jié)角 部分逆解結(jié)果

3）測試網(wǎng)絡(luò)泛化能力

圖1 測試輸出誤差

4）兩種算法的比較

具體內(nèi)容及運行結(jié)果如表2所示。EC-RBF學(xué)習(xí)算法中所得聚類中心數(shù)目分別為43和139。

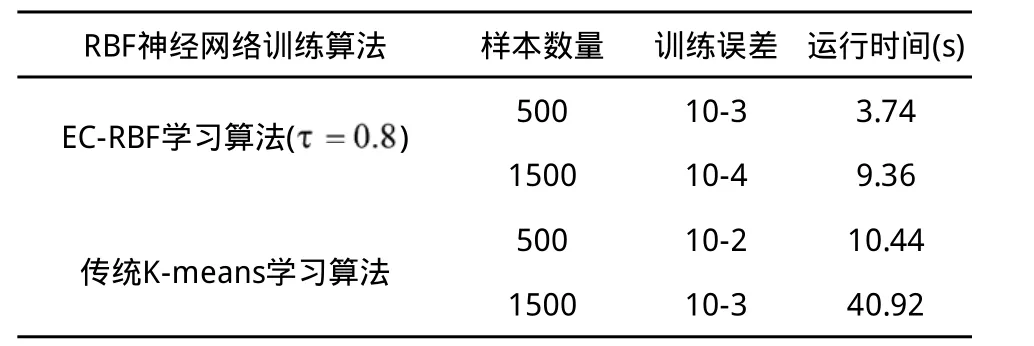
表2 兩種算法的比較

分析上述結(jié)果，由表1可以看到網(wǎng)絡(luò)實際輸出與期望輸出的均方誤差數(shù)量級基本上控制在10-3，符合網(wǎng)絡(luò)設(shè)計之初的目標。由網(wǎng)絡(luò)的測試輸出可以看到，基于熵聚類算法的EC-RBF神經(jīng)網(wǎng)絡(luò)具有很好的泛化能力，對于網(wǎng)絡(luò)訓(xùn)練樣本之外的數(shù)據(jù)仍然有很好的計算能力，能夠滿足機械臂關(guān)節(jié)角度的精度要求，對機械臂運動學(xué)逆解問題具有很好的解決能力。在網(wǎng)絡(luò)訓(xùn)練過程中，相比傳統(tǒng)K-m eans算法，EC-RBF算法計算精度更高，且在訓(xùn)練樣本數(shù)量較大時，極大的加速了數(shù)據(jù)聚類過程，從而提高RBF網(wǎng)絡(luò)的訓(xùn)練速度，為機械臂控制器設(shè)計節(jié)省了時間，以達到實時性要求。

4 結(jié)論

基于熵聚類學(xué)習(xí)算法的EC-RBF神經(jīng)網(wǎng)絡(luò)，在很大程度上克服了傳統(tǒng)K-m eans學(xué)習(xí)算法在中心值和類別數(shù)初值取值上的不確定性，使其更快速收斂，從而加速網(wǎng)絡(luò)的訓(xùn)練過程。將EC-RBF神經(jīng)網(wǎng)絡(luò)用于機械臂的運動控制中，仿真結(jié)果表明在求解機械臂逆問題過程中，避免了繁瑣的公式推導(dǎo)，在數(shù)據(jù)樣本巨大時，大大的減小了計算量，比運用傳統(tǒng)RBF網(wǎng)絡(luò)進行逆問題求解具有更快的處理速度，并且具有很好的求解精度。同時，也為后續(xù)機械臂嵌入式運動控制器的開發(fā)與實現(xiàn)提供了理論基礎(chǔ)。

[1] 蔡自新.機器人學(xué)(第二版)[M].北京:清華大學(xué)出版社,2007.

[2] 楊國軍,崔平遠.機械手逆運動學(xué)神經(jīng)網(wǎng)絡(luò)建模與仿真[J].系統(tǒng)工程與電子技術(shù),2001,23(1):55-58.

[3] Li Zhem ing, Li Chungui, Lv Shao jiao. A Method fo r So lving Inverse Kinem atics o f PUMA560 Manipu lator Based on PSO -RBF Netw o rk[C]//8th In ternational Con ference on Natu ral Com pu tation , 2012:298-301.

[4] 榮盤祥,楊晶,胡林果,馬廣富.基于RBF網(wǎng)絡(luò)的SCARA機器人的運動學(xué)逆解[J].電機與控制學(xué)報,2007,11(3):303-305.

[5] 盛黨紅,溫秀蘭,黃文良.基于免疫進化神經(jīng)網(wǎng)絡(luò)的機械手逆運動控制[J].中國機械工程,2007,18(3):282-285.

[6] 陳勇,鄭加強,郭偉斌.除草機器人機械臂運動分析與控制[J].農(nóng)業(yè)機械學(xué)報,2007,38(8):105-108.

[7] 王華麗,周尚波.基于熵聚類的RBF神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)算法[J].計算機仿真,2008,25(11):168-171.

[8] J.Yao,M.Dash, S.T. Tan, et al. En tropy-based Fuzzy Clustering and Modeling [J]. Fuzzy Sets and System s,2000, 113(3)382-388.