矢量聲納高速運動目標穩健高分辨方位估計*

梁國龍 馬巍 范展 王逸林

(哈爾濱工程大學,水聲技術重點實驗室,哈爾濱 150001)

(2012年11月28日收到;2013年1月31日收到修改稿)

1 引言

作為水下作戰平臺近乎惟一的“耳目”,利用水下聲信息進行探測、識別、定位、導航和通信的廣義聲納系統,在容許的應用環境中大多采用聲納陣列的形式進行所需信號處理,以獲得可控的陣列指向性和較高的空間處理增益.空間譜估計是水聲陣列信號處理最主要的研究方向之一,其旨在研究空間多傳感器陣列聲納所構成的處理系統對感興趣的空間信號參數進行準確估計的能力,主要用于估計信號的空域參數或信源位置.近些年來,隨著聲矢量傳感器技術在理論分析、性能評估和工程實踐上的研究應用迅猛發展,基于聲矢量傳感器的方位(direction of arrival,DOA)估計技術得到較為深入的研究[1-7].以多重信號分類(multiple signal classifi cation,MUSIC)算法為代表的大多數高分辨子空間類算法[8-10],由于需要對接收數據協方差矩陣進行有效估計,對于空域接收數據快拍數提出了較高的要求.然而對于大多數有意義的應用環境而言,大快拍數據往往不易得到.特別是對于聲納陣列的實際作戰應用環境中,大量出現的是高速運動目標或瞬態信號,戰機往往轉瞬即逝,此時獲取的有意義數據快拍通常較少,極惡劣情況下其有效數據甚至可能出現單快拍情況,上述的高分辨算法將由于得不到有效的協方差估計矩陣而失效.為了解決小快拍數條件下的穩健高分辨DOA估計問題,Sarkar等[11-14]提出了直接數據域方法(direct data domain,DDD),與傳統統計方法相比,它具有單快拍處理的優勢,且避免了樣本協方差矩陣的構造及求逆運算.文獻[15—19]的壓縮感知理論(compressive sensing,CS)利用信號稀疏特性可對原始信號進行重構;Maliotov等[20,21]以類似的思想提出利用信號稀疏分解進行DOA估計的方法;付金山[22]將信號稀疏分解理論運用到了矢量傳感器陣列信號處理中.

上述方法大多需要較高的輸入信噪比門限,否則其估計性能將大幅下降.然而在矢量聲納陣列應用環境下,信噪比與快拍數一樣往往不能達到較理想的狀況.針對這樣的限制條件,本文利用聲矢量傳感器的結構特性,引入空域濾波技術[23],提出將聲壓振速聯合處理技術與空域濾波技術聯合使用的時空濾波壓縮感知DOA估計方法,大大減小了輸入信噪比門限,同時利用小快拍數據可有效估計高速運動目標或瞬態信號的瞬時方位,具有較強的魯棒性.

2 聲矢量傳感器基本原理

2.1 聲矢量傳感器模型

矢量傳感器由聲壓水聽器和質點振速水聽器復合而成.聲壓水聽器測量空間的聲壓P,質點振速水聽器測量聲場中的質點振動速度Vx,Vy,因此矢量傳感器可以共點、同步測量聲場的聲壓標量和質點振速矢量.典型的聲矢量傳感器如圖1所示.

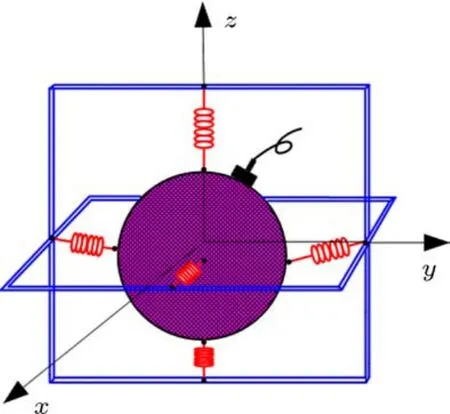
圖1 聲矢量傳感器模型

均勻各向同性的非黏滯流體傳播介質中,Euler方程可以寫成

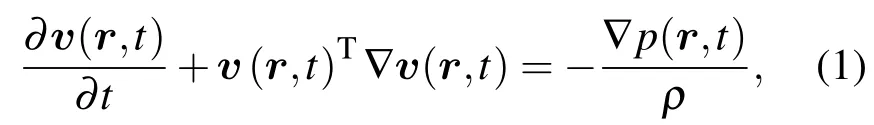
其中,p(r,t)表示t時刻聲場中r位置處的聲壓,v(r,t)代表該點處的振速,ρ表示介質密度.考慮遠場平面波條件,則聲壓函數可以寫成

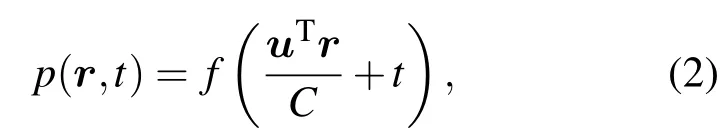
其中,uT=[sin(θ)cos(φ),sin(θ)sin(φ),cos(φ)]代表聲矢量傳感器的方向向量,θ和φ分別表示信號的水平方位角和垂直俯仰角,C代表介質中的聲速.進而可將聲壓梯度表示為

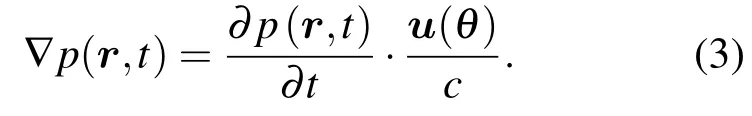
對于聲波傳播背景而言,線性化(1)式,并可忽略其中的振動加速度項,結合以上各式可得：

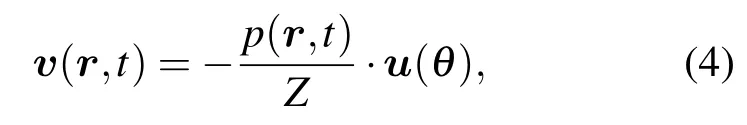
其中,Z=ρC表示平面波波阻抗.

不失一般性,考慮二維聲矢量傳感器模型,則其聲壓振速3通道接收數據模型可以描述為

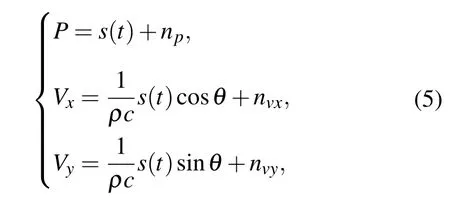
其中,s(t)為原始信源數據,np,nvx,nvy分別為各通道噪聲.

2.2 聲矢量傳感器陣列測量模型

考慮二維各向同性噪聲場中,遠場窄帶信源入射到任意幾何形狀矢量聲納陣列,假設陣元數為M,信源數為N(N＜M).各信源中心頻率為 fl,入射角度為θl,l=1,2,···,N,定義為信源與聲矢量傳感器陣列法向夾角.以陣列最左端陣元為參考坐標系原點,則陣列接收的快拍數據可以表示為

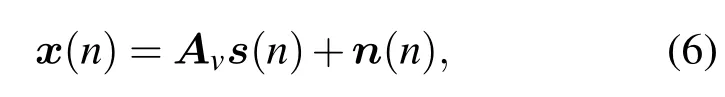
其中,

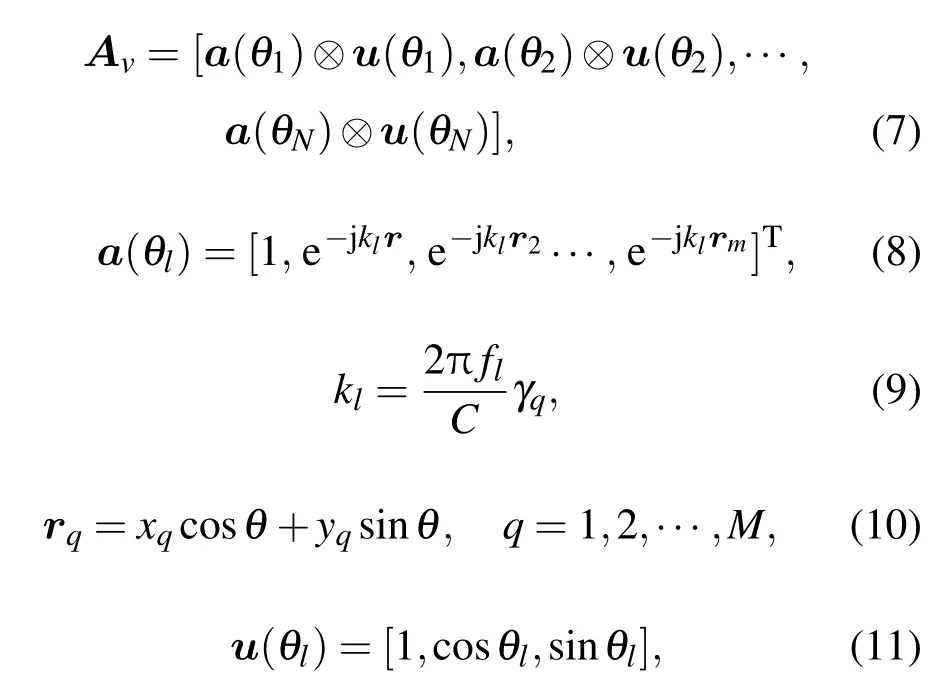
Av為導向矢量矩陣,a(θl)為第l個信源在傳感器陣列上的陣列流型矢量,kl為第l個入射信源的波數,rq代表第q個陣元的空間位置矢量,u(θl)表示第l個信源的方向矢量.

3 聲矢量傳感器聲壓振速聯合時域濾波方法設計

(5)式描述的聲矢量傳感器的結構特性表明,均勻無限介質中平面波相干輻射源聲場內部,聲壓與振速各通道信號完全相關.平面波聲場中,波阻抗Z=ρC為實數,因而相干信號的聲壓與振速相位是相同或相反的.

與之不同的是在各向同性噪聲場中,假設np(t)為入射角不同的 j個互不相關各態歷經隨機噪聲聲壓,且滿足,則其水平、垂直振速可以表示為

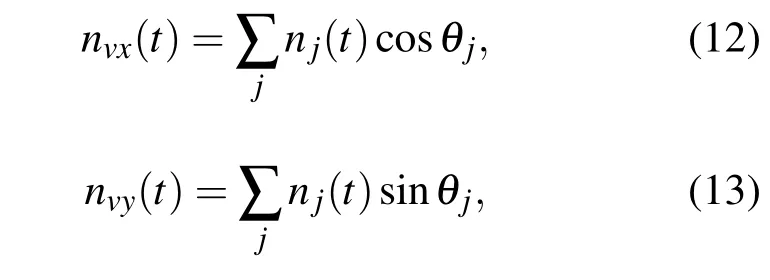
其中,θj為[0,2π]內均勻分布的隨機變量.聲壓與振速的相關系數可以表示為

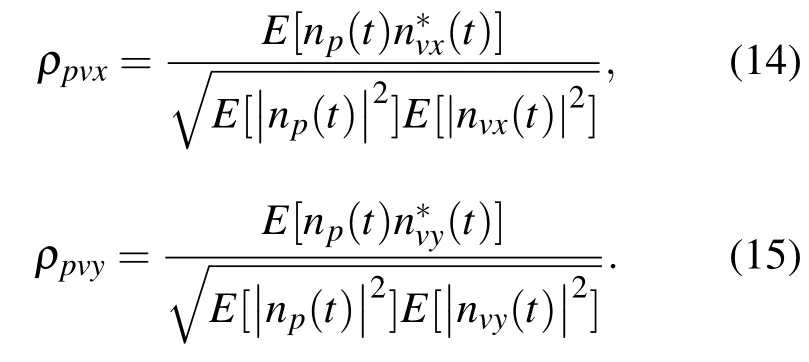
分√別記聲壓與兩振速標準差之積為kpvi=整理可得：

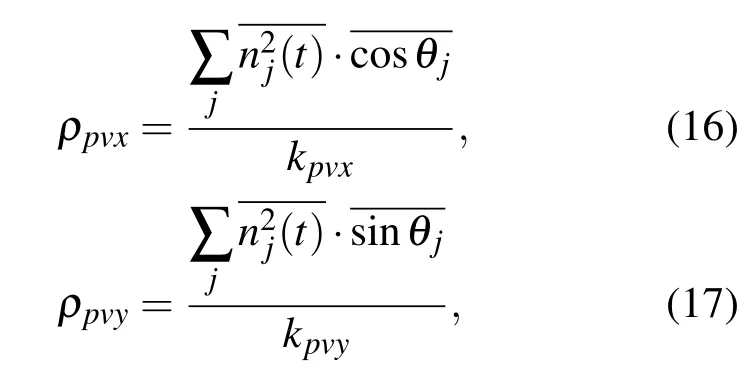
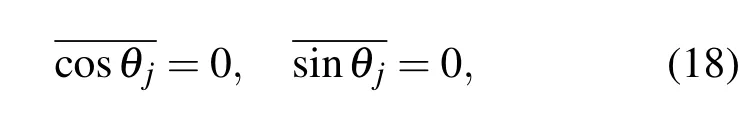
即各向同性噪聲場中聲壓與振速相關系數為0.這意味著在上述信號、噪聲場中,對于聲矢量信號的聲壓振速聯合處理對于噪聲具有抑制作用.

對于聲矢量傳感器數據通道做旋轉組合變換,定義旋轉變換后數據為

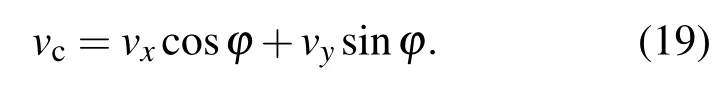
整理(13)式并注意到(5)式可得：

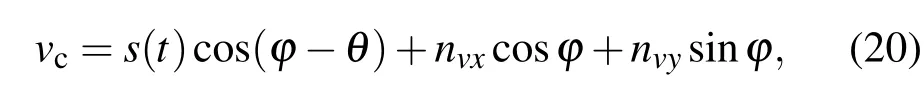
其中,φ為電子旋轉角.將聲壓通道數據與上述旋轉變換數據進行組合,采用(p+vc)vc的組合形式,考慮上述信號噪聲相關特性,其一階矩可表示為

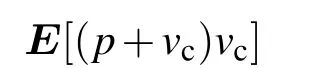
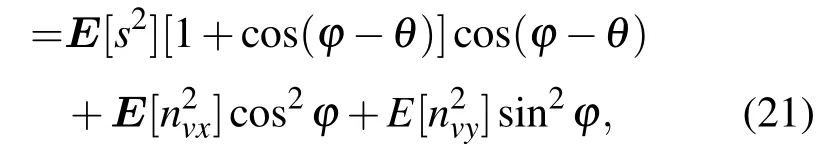
這意味著通過將聲矢量傳感器數據進行旋轉組合,并選擇合適的旋轉角φ可以減小噪聲,從而降低信噪比門限,為探索遠距離微弱目標提供了可能.圖2給出了旋轉角為60°時,旋轉組合后單個聲矢量傳感器的指向性圖.

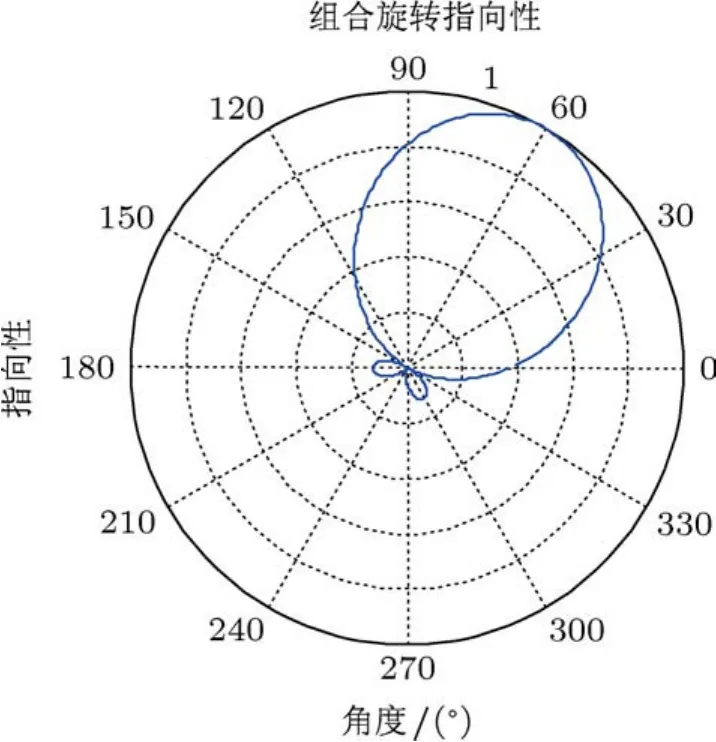
圖2 以60°組合旋轉后的指向性圖

利用信噪相關特性上的差異進行降噪處理,因而聲壓振速聯合處理抗噪方式屬于一種廣義時域濾波.

4 阻帶衰減通帶均方誤差最大值最小矩陣空域濾波器設計

矩陣空域濾波技術(matrix filter,MF)是一種陣元域數據預處理算法,通過設計阻帶與通帶扇面的空域幅頻響應實現對信號的預濾波,從而降低信號處理信噪比門限.考慮2.2節所述聲矢量傳感器陣列模型,設計濾波矩陣F對輸入數據進行空域濾波,則(6)式改寫為

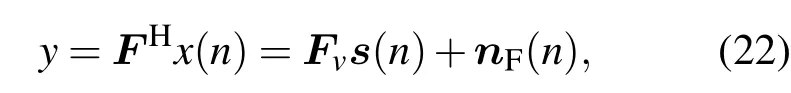
其中,Fv=FHAv表示矩陣濾波后的聲量傳感器陣列流型矩陣,nF(n)=Fvn(n)表示矩陣濾波后的噪聲數據矩陣.MF方法的基本思想是設計矩陣濾波器,使其空域幅頻響應滿足對于空域預成方位扇面保證無失真通過,對于其他方位扇面形成某可控衰減,即為空域帶通濾波器.其思想可以表述為

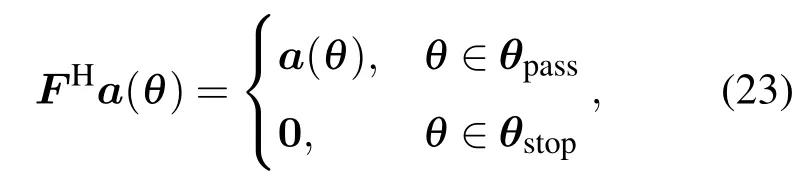
其中θpass,θstop分別表示空域濾波器的理想通帶與阻帶.我們希望設計出的矩陣濾波器可以滿足在通帶內由其與原始陣列流型組合產生的新陣列流型變化的均方誤差最大值最小,在阻帶扇面內將輸出功率減至某指定值.按照這樣的思想,矩陣濾波器優化設計問題可以表述為

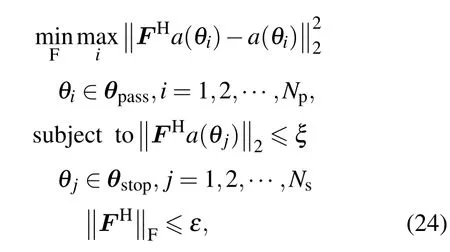
其中,i,j分別代表通帶與阻帶內的離散方位分辨率,Np,Ns分別表示通帶與阻帶扇面內離散出的方位個數,‖·‖F表示Frobenius范數,ξ為阻帶內的衰減率,ε為濾波后噪聲功率門限.上述優化問題可參考文獻[23]給出的方法,將濾波器設計轉化成二階錐規劃問題進行求解.

5 時空聯合濾波壓縮感知方位估計

壓縮感知技術利用信號在某域的稀疏特性,通過構造觀測基或冗余字典對信號進行非自適應隨機投影測量,隨后通過求解L范數優化問題使信源信號能夠以很高的概率精確重建.將CS技術做適宜水聲矢量信號處理框架的變形,聯合前文提出的時域和空域濾波方法,采用CS技術進行矢量聲納空間譜估計,理論上可以大大減小所需的處理信噪比門限,并在小快拍數情況下取得較好估計效果.

5.1 矢量聲納陣列空間譜稀疏性分析

不失一般性,考慮水聲環境中水平均勻半波間隔矢量聲納直線陣,其余條件如2.2節所述.對于(6)式的基本模型而言,s(n)為N×α維,α表示空域采樣快拍數,其含義為空間每信源α點采樣的N個原始信源集合.如果將全空間方位離散化,并假設離散分辨率為η,(η＞0),則s(n)必可表示為全空間方位中round(2π/η)個離散角度信源的線性組合,round(·)表示對變量取整.其在對應的目標θi角度中表示系數1,其他方位為0.省略宗量n,上述原理的數學表述為

其中,β為round(2π/η)×α維空域稀疏表示系數,ψ為N×round(2π/η)維空域稀疏變換基.通過設置合適的空域分辨率η,可滿足N?round(2π/η),即保證了β是空域N行稀疏的.圖3為上述變換的示意圖,其中實心圓點代表真實目標,空心圓點代表空域離散點.

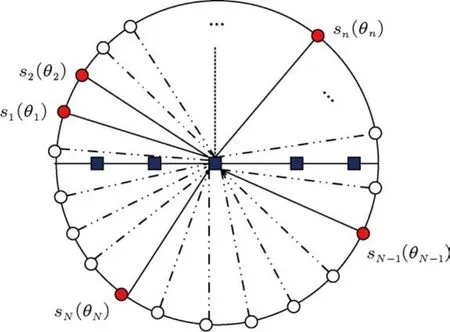
圖3 矢量聲納空域稀疏分解示意圖

從另一個角度而言,根據(8)式矢量聲納陣列空間數據接收模型可認為是空域有限復單頻信號的疊加,因而原始數據經空域傅里葉變換到空間域中,其表示系數也必然是稀疏的.

5.2 矢量聲納陣列壓縮感知方位估計方法感知矩陣的構建

CS理論對于觀測基的選取要求其與稀疏基不相關,這里的相關性可以理解為相互表示時所需的表示系數個數,非相關性越強,利用CS理論進行稀疏系數優化求解的成功概率就越高.考慮對空間信號進行隨機采樣,即將矢量聲納進行隨機布放,因而聲壓振速各通道的接收數據可認為是對原始信號s的行隨機抽取,可表述為

其中,R表示上述定義的行隨機矩陣.利用(24)式可得：

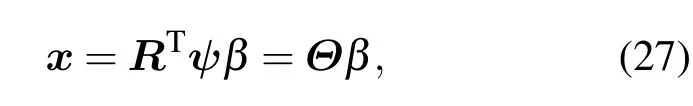
Θ為原始信號稀疏至空域后的行隨機抽取矩陣.布陣方式導致的矢量聲納陣列流型隨機性可看作對稀疏信號的行隨機投影測量,因而其與稀疏基具有很強的非相關性.這樣的非相關性與約束等距條件(restricted isometry property,RIP)是等價的,二者都是可精確重構稀疏信號的充分條件,因而保證了矢量聲納壓縮感知DOA方法的穩健性.實際應用中,當隨機布陣結束后,利用已知的陣元位置可精確得到陣列流型矩陣Av,并與空域濾波矩陣相乘得到新的陣列流型Fv,進而構建全部從0至round(2π/η)方位的陣列流型作為過完備冗余字典即可得到感知矩陣Θ.

5.3 矢量聲納陣列時空聯合濾波壓縮感知方位估計方法

分別利用前述的旋轉組合時域濾波方法和矩陣空域預濾波方法進行預處理后,矢量聲納陣列時空聯合濾波壓縮感知方位估計方法(vector sonar array time space fi ltered compressive sensing DOA,VTSCS)的基本原理可以表述為已知輸入陣列接收數據x和人為構造的空域過完備冗余字典Θ,求解(26)式中信號稀疏表示β的問題.一個比較自然的想法是求解下述0范數最優化問題：

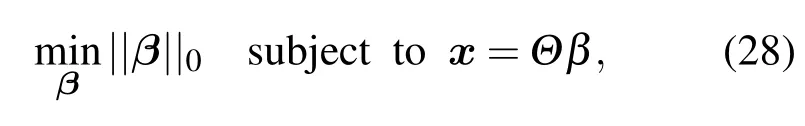
其中0范數代表稀疏表示β中非零項的個數,然而這是一個NP-HARD問題,精確解的獲得需要遍歷所有的可能解,從而使計算復雜性大大增強.文獻[17]表明如果采用1范數代替0范數進行優化求解,則可得到如下的凸優化問題：

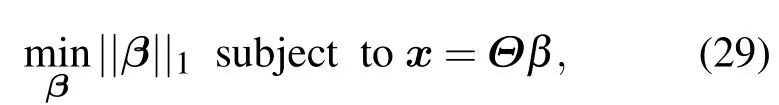
且在滿足一定條件時,上述兩式是等價的.考慮含噪聲的情況下,可改寫(28)式為如下的凸優化問題：

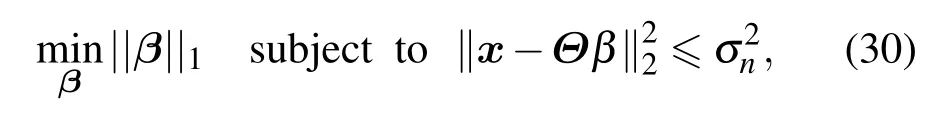
其中,σn2是對噪聲功率的一個估值.實際應用中,可采用一階遞歸濾波的形式對當前噪聲功率進行實時在線估計.

需要說明的是,(29)式對于單快拍情況是典型的凸優化表示,因而具有良好的優化解.而對于多快拍聯合估計,(29)式是非凸的,應考慮將多快拍數據進行綜合處理,即將其考慮成各單快拍數據的組合,進而將估計得到的稀疏表示結果β表示成利用各單快拍估計得到的結果的加權形式,即

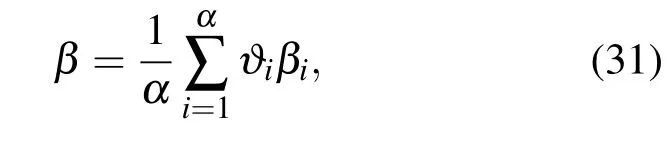
其中,βi表示利用第i個快拍數據估計得到的稀疏表示結果,?i為利用第i個快拍數據估值的懲罰因子,表示目標高速運動時可利用的當前快拍數據的置信程度,滿足?i∈[0,1].聯合求解(29),(30)式即可得到原始信號的空域稀疏表示,由于其是空域N行稀疏的,因而β中N個非零項的對應位置與空域分辨率之積即為目標的DOA值.圖4所示為VTSCS方法的信號處理流程.

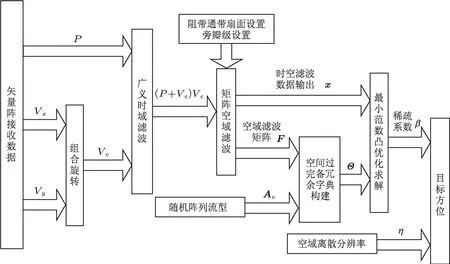
圖4 VTSCS方法信號處理流程圖

此外對于寬帶形式信號,可對原始時域信號做傅里葉變換,進而在得到的每個頻域子窄帶上采用VTSCS方法進行DOA估計.

6 數值仿真試驗分析

考慮各向同性噪聲場中,遠場等功率非相干窄帶雙目標入射至10元矢量聲納隨機陣型陣列.入射角度分別為30°,50°,頻率分別為1 kHz,2 kHz,采樣頻率10 kHz,輸入信噪比為20 dB,快拍數為200.如無特殊說明,均采用以上基本試驗條件.為便于分析說明仿真結果,分別將VTSCS方法與基于矢量常規波束形成的DOA估計方法(vector conventional beamforming,VCBF)、矢量最小方差無畸變響應方法(vector minimum variance distortionlessresponse,VMVDR)和矢量MUSIC方法(vector MUSIC,VMUSIC)進行DOA估計性能比較.其中,圖5給出了各種方法DOA估計的譜峰顯示,圖6—8分別給出了以信噪比、快拍數和信源入射角度間隔為變量時的DOA估計性能.性能優劣評價標準除可視的譜峰輸出外,根據變化條件的不同,主要考察各方法多次DOA估計的均方根偏差(root mean squareerror,RMSE)或成功概率(success probability,SP).

定義N 次信源方位估計的RMSE為

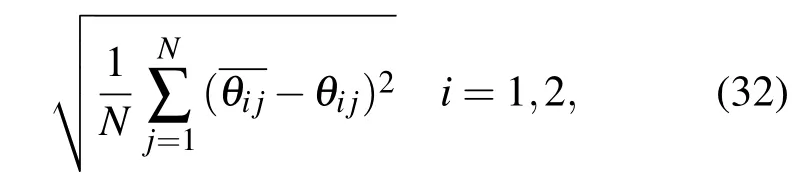
其中,θij和分別表示第i個信源第 j次試驗的真值和估計值.

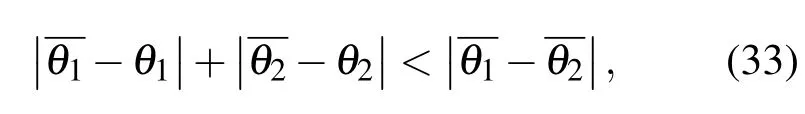
SP即為成功的估計次數占估計總數的百分比.

圖5給出了前述基本條件下各種方法的空間譜估計圖.從中可以看出當信噪比與快拍數均較高時,除VCBF方法估計性能較差外,其余各種方法均能給出目標較準確的方位估計,其中VTSCS方法的可分辨信噪比門限要遠低于前述各種方法.

圖6給出了快拍數為200,入射角度間隔20°時各種方法RMSE隨信噪比變化示意圖.從插圖中可以看出在低信噪比條件下,VTSCS比其他方法具有更好的DOA估計性能.隨著信噪比的逐漸增加,各種方法的估計RMSE逐漸減小.其中VMUSIC方法的RMSE最小,VTSCS方法略遜于VMUSIC.考慮到較高信噪比時VTSCS的估計RMSE僅比VMUSIC方法大0.02°左右,因此可認為VTSCS方法與VMUSIC方法具有類似的DOA估計精度,在高信噪比條件時近似是無偏估計.

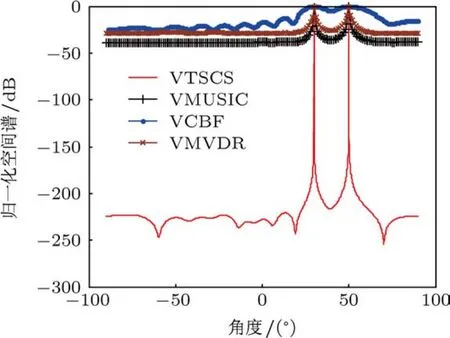
圖5 DOA估計性能比較圖

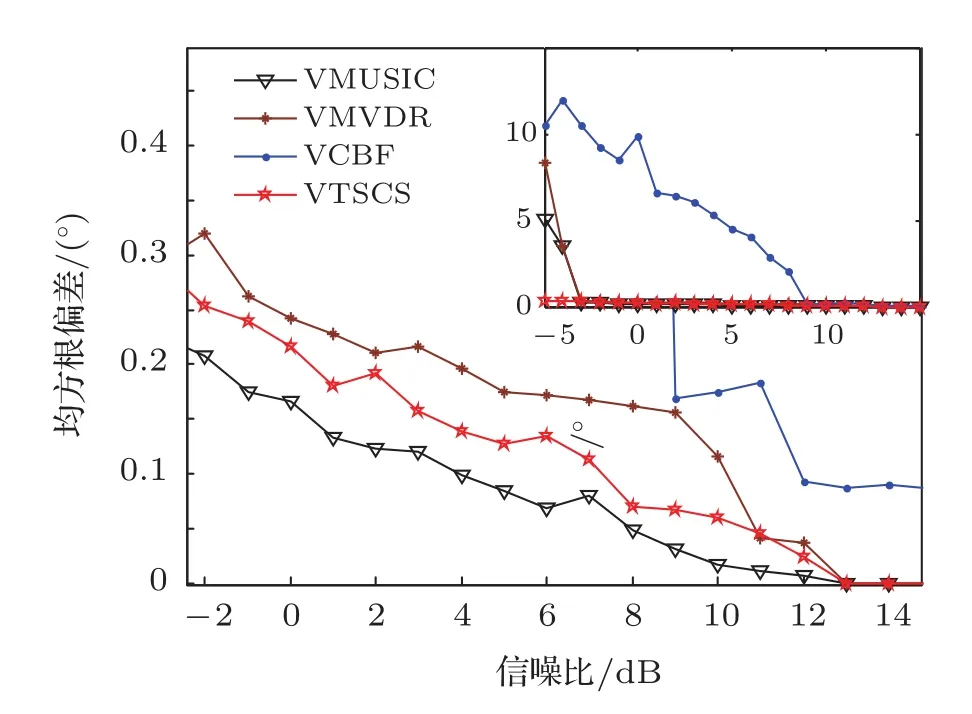
圖6 不同信噪比條件下各種方法估計均方根偏差比較

圖7 給出了信噪比0 dB,入射角度間隔20°時各種方法RMSE隨快拍數變化示意圖.從插圖中可以看出VTSCS方法對快拍數不敏感,在單快拍情況下其RMSE仍只有0.5°左右,具有較強的穩健性.其他各方法估計性能都受到快拍數的限制,其中在較低快拍數情況下,由于子空間分解對于快拍數有著更高的要求,VMUSIC方法具有比VMVDR方法更大的RMSE,而隨著快拍數的逐漸增加,VMUSIC方法RMSE逐漸減小.VTSCS方法始終具有最低的DOA估計RMSE.

圖8給出了信噪比0 dB,快拍數為200時各種方法SP隨入射角度間隔變化示意圖.從中可以看出隨著入射信源角度間隔的增加,各種方法的估計成功概率都有所提高.其中,VTSCS方法對于角度間隔具有最好的穩健性,在約5°雙目標分辨概率可達90%,VMUSIC方法的角度分辨力要強于VMVDR方法和VCBF方法.

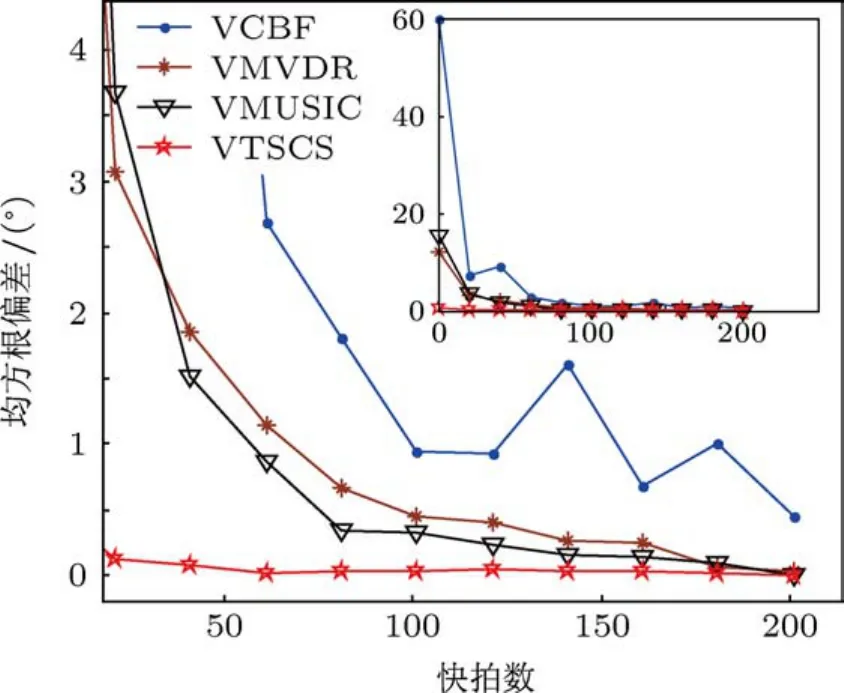
圖7 不同快拍數條件下各種方法估計均方根偏差比較

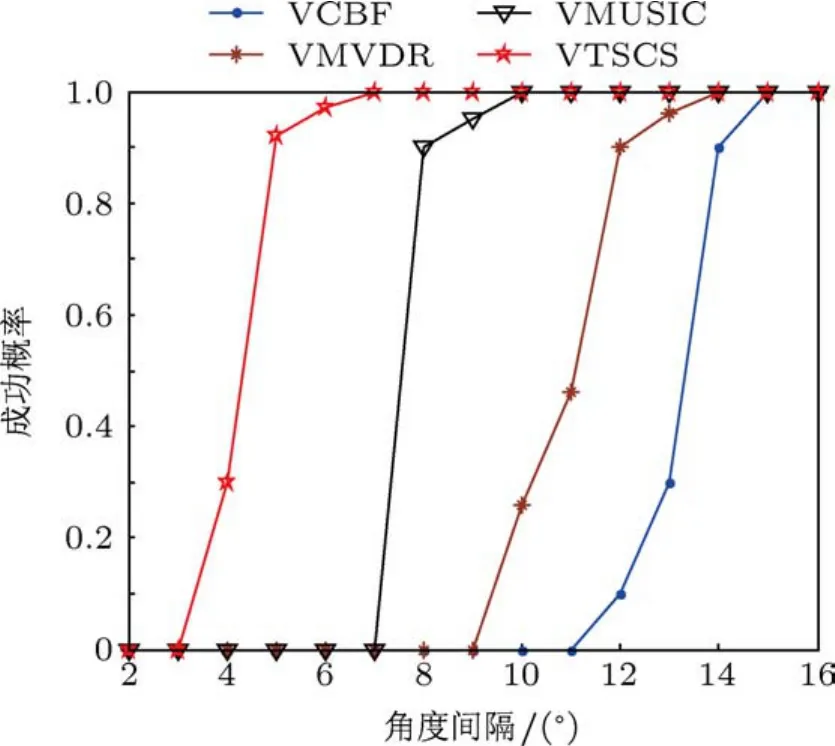
圖8 不同入射信源角度間隔條件下各種方法估計成功概率比較

圖9 單快拍條件下各種方法空間譜圖

考慮矢量聲納陣應用背景下雙目標高速運動的極端情況,即假定只有單快拍數據有效,其余基本條件不變.圖9給出了此時上述各種方法的空間譜圖.可以看出,由于VMVDR和VMUSIC方法的DOA估計性能嚴重依賴于數據協方差矩陣的估計程度,因此對于單快拍情況,這兩種方法已經失效.此時,VTSCS方法仍具有較高的雙目標分辨門限,但估計精度有所下降.值得說明的是,雖然在前述各種條件下的性能比較時VCBF方法的性能總是最差,但此時仍具有一定的雙目標分辨能力,因而VCBF方法也具有較強的魯棒性.

7 湖上試驗驗證

為驗證VTSCS方法的有效性,于某自然水域進行了相關試驗.試驗采用6元矢量陣,布放于測量船下深度約10 m,陣間距1.5 m.兩非相關窄帶聲源布于同深度,距離6元陣聲中心距離100 m左右,入射角約為20°,74°,頻率分別為1 kHz,2 kHz,系統采樣頻率20 kHz,陣列輸入信噪比約為10 dB.圖10所示為系統構建示意圖.

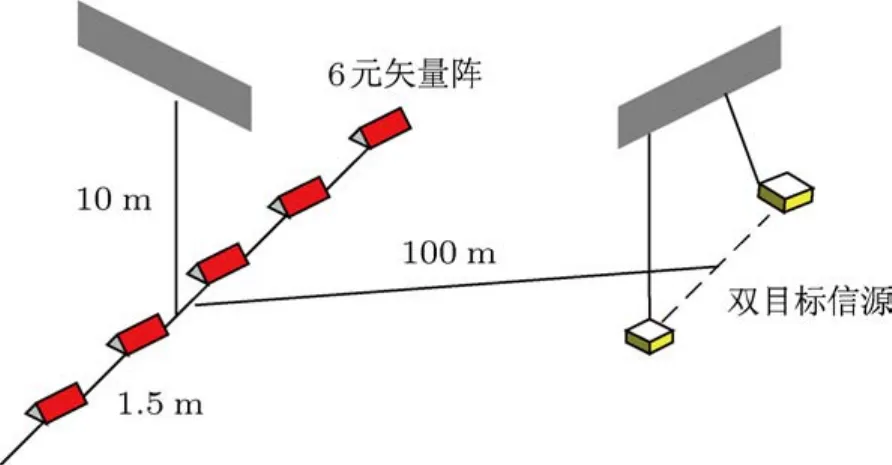
圖10 湖上試驗示意圖

取單快拍數據,利用一階遞歸方法估計當前噪聲功率,并設置(30)式中合適的噪聲功率門限值.對此數據分別利用VCBF,VMVDR,VMUSIC和VTSCS方法進行DOA估計,其空間譜輸出如圖11所示.

從圖中可以看出,與理論分析一致,單快拍時VMUSIC與VMVDR方法均已失效.VCBF方法具有分辨雙目標的能力,但精度不高.VTSCS方法具有較好的雙目標分辨門限,但此時精度也已降低,其RMSE約為4°.

值得說明的是,噪聲功率門限的設定對于VTSCS方法的性能有著重要影響.圖12和圖13分別給出了噪聲功率門限設置過低和過高時VTSCS方法的空間譜圖.

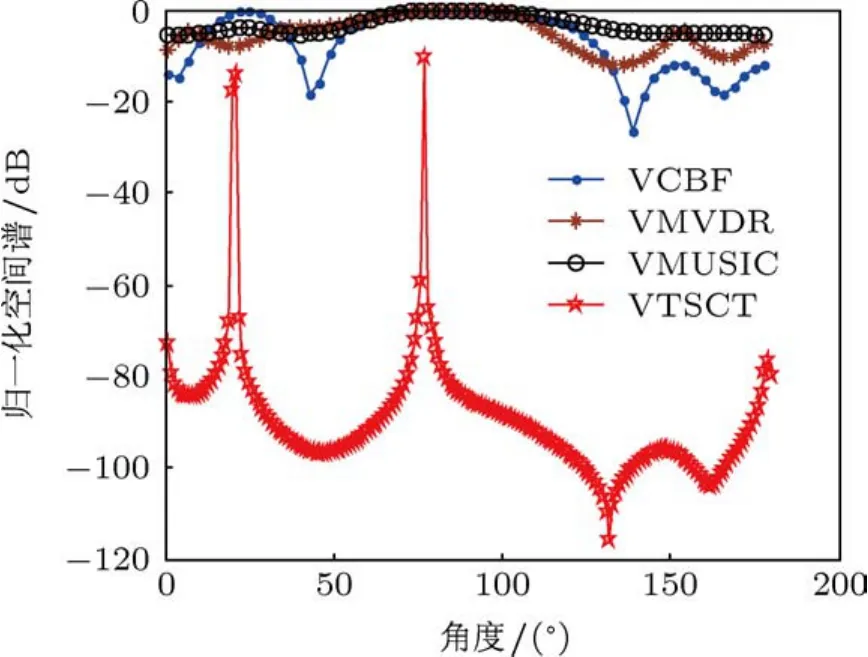
圖11 湖上試驗空間譜圖

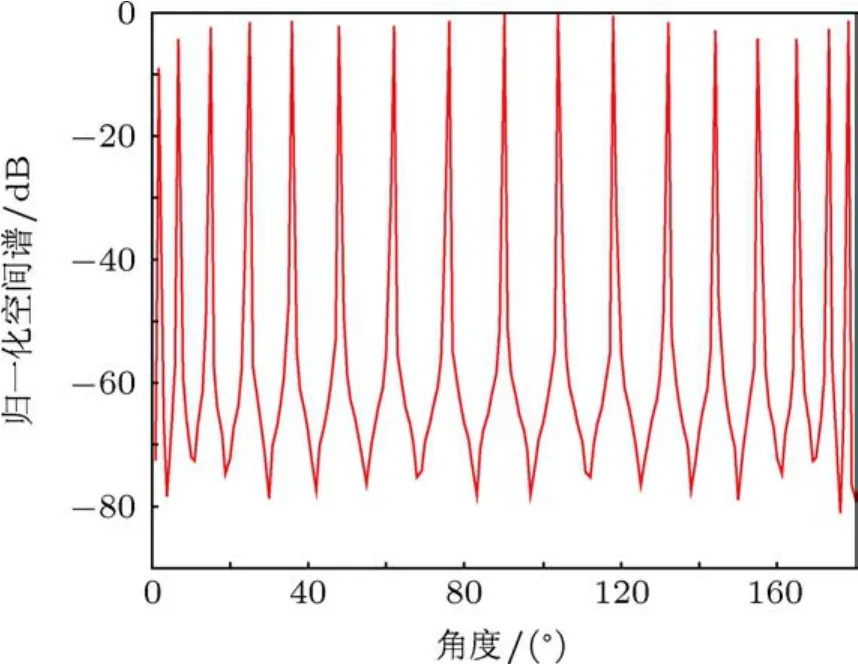
圖12 噪聲功率門限過低時VTSCS空間譜圖

湖試結果表明,當噪聲功率設置過低時,意味著提高了對于(30)式中可存在的噪聲功率的要求,即對凸優化求解過程的限制條件更苛刻.此時利用凸優化可能無法得到全局最優解,進而會用一系列的局部最優值來進行替代,因而會出現一系列偽峰.當噪聲功率設置過高時,對于(30)式中噪聲功率的約束過小,噪聲的存在將嚴重影響信源的空域稀疏性,因而無法得到正確的DOA估計.

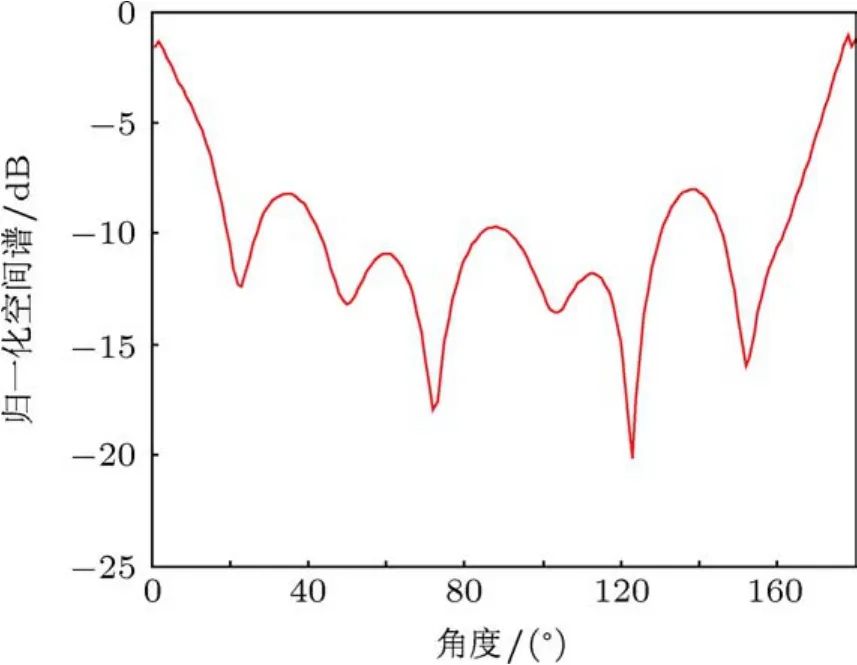
圖13 噪聲功率門限過高時VTSCS空間譜圖

8 結論

提出了一種矢量聲納陣高速運動目標穩健高分辨方位估計方法.該方法分別利用聲矢量傳感器聲壓振速聯合處理的廣義時域濾波和阻帶約束通帶均方誤差最大值最小矩陣空域濾波進行前置處理,進而利用矢量陣空域目標稀疏特性,結合壓縮感知理論進行空間譜估計.理論分析與數值仿真表明,與經典的VCBF,VMVDR,VMUSIC方法相比,新方法利用小快拍數據即可獲得較低的雙目標分辨門限和較高的估計精度,具有較高的小快拍(單快拍)數據DOA估計穩健性,為遠程微弱高速運動目標的方位估計問題提供了新的解決思路.湖試結果驗證了該方法的有效性.

[1]Nehorai A,Paldi E 1994 IEEETrans.on SP 42 2481

[2]Hui JY,Liu H,Yu H B,Fan M Y 2000 Acta Acustica 25 303(in Chinese)[惠俊英,劉宏,余華兵,范敏毅2000聲學學報25 303]

[3]Shi J,Yang D S,Shi SG 2012 Acta Phys.Sin.61 4302(in Chinese)[時潔,楊德森,時勝國2012物理學報61 4302]

[4]Yang SE 2003 J.Harbin Engin.Univ.24 591(in Chinese)[楊士莪2003哈爾濱工程大學學報24 591]

[5]Wu Y Q 2011 Ph.D.Dissertation(Changsha：National University of Defense Technology)(in Chinese)[吳艷群2011博士學位論文(長沙：國防科學技術大學)]

[6]Sun GQ,Li QH 2004 Acta Acustica 29 491(in Chinese)[孫貴青,李啟虎2004聲學學報24 491]

[7]Chen X H 2004 Ph.D.Dissertation(Harbin：Harbin Engineering University)(in Chinese)[陳新華2004博士學位論文(哈爾濱：哈爾濱工程大學)]

[8]Schmidt RO 1986 IEEETrans.on AP 34 276

[9]Capon J1969 Proceedingsof the IEEE 57 1408

[10]Roy R,Kailath T 1989 IEEETrans.on ASAP 37 984

[11]Sarkar T K,Sangruji N 1989 IEEETrans.on ASAP 37 940

[12]Sarkar T K 2003 Smart Antennas(1st Ed.)(New Jersey：John Wiley&Sons Inc.)p52

[13]Sarkar T K,Koh J,Adve R,Schneible R A,Wicks M C,Choi S,Salazar-Palma M 2000 Antennasand Propagation Magazine42 39

[14]Sarkar T K,Sangruji N,Micheal CW 1998 Digital Signal Processing 8 114

[15]Donoho D L 2006 IEEETrans.Inform.Theory 52 1289

[16]Candes E J,Walkin M B 2008 IEEE Signal Processing Magazine 25 21

[17]Candes EJ,Romberg,Tao T 2006 IEEETrans.Inform.Theory 52 489

[18]Candes EJ,Tao T 2006 IEEETrans.Inform.Theory 52 5406

[19]Candes EJ,Romberg,Tao T 2006 Comm.Pure Appl.Math.59 1207

[20]Malioutov D M 2003 M.S.Dissertation(Cambridge：Massachusetts Institute of Technology)

[21]Malioutov D M,Cetin M,Willsky A S 2005 IEEE Trans.on SP 53 3010

[22]Fu JS2012 Ph.D.Dissertation(Harbin：Harbin Engineering University)(in Chinese)[付金山2012博士學位論文(哈爾濱：哈爾濱工程大學)]

[23]Yan SF,Ma Y L 2006 Sci.China Inf.Sci.36 153(in Chinese)[鄢社鋒,馬遠良2006中國科學·信息科學36 153]

[24]Gershman A B 1998 IEEETrans.on SP.44 361