基于電諧振單元的超介質吸波材料及矩形波導匹配終端應用研究*

李建 文光俊 黃勇軍 王平 孫元華

(電子科技大學通信與信息工程學院,光纖傳感與通信教育部重點實驗室,成都 611731)

(2012年11月20日收到;2012年12月20日收到修改稿)

1 引言

超介質(metamaterial)是指一種自然界不存在的人工合成材料.1968年,前蘇聯科學家Veselago[1]理論分析了電磁波在介電常數ε(ω)和磁導率μ(ω)同時為負的各向同性均勻超介質中的電動力學行為,并預見了該類材料具有常規材料所不具有的一些獨特電磁特性,如逆折射效應、逆多普勒頻移效應、逆切連科夫輻射、負光壓等.2000年,美國加州大學圣迭戈分校Smith等[2]采用金屬導體線和金屬諧振環相重疊的微結構為基本單元,首次人工合成出X波段超介質,同年英國帝國理工學院Pendry教授[3]提出了應用超介質實現完美透鏡的可行性.2001年,Shelby等[4]通過實驗測試證實了由Smith所設計的劈行二維超介質樣品的負折射現象.這些研究成果開創了超介質的人工合成方法、機理、應用研究之先河,引起了國內外學者的極大研究興趣,使超介質技術研究成為當今國際物理學界和電磁學界的前沿研究領域.

2000年始,超介質的研究主要集中在其實現機制探索[5-15]、奇異電磁特性分析[16-19]、應用研究[20-26]等方面.其中,基于超介質的吸波材料由于具有近理想的吸波性能而受到廣泛關注[20-24].2008年,Landy等[27]首次研究實現了微波頻段的基于電諧振環與短路金屬線陣列的超介質吸波材料.隨后,眾多結構的超介質吸波材料被提出[28].其中,平面超介質吸波材料的主要實現結構為：在介質基板一面刻蝕出超介質金屬諧振單元,另一面完全覆上金屬.其吸波原理為：采用電諧振結構單負超介質實現電諧振特性,基于電諧振結構與介質層另一面的金屬平板之間的耦合作用,將在金屬平板上產生反向的表面電流,從而在金屬諧振環與金屬平板之間形成磁諧振.通過調節優化超介質的結構參數,使得其等效阻抗與自由空間波阻抗匹配,以及在匹配工作頻段內具有高損耗特性(包括金屬的歐姆損耗和介質的介電損耗),最終達到完美吸波特性.

另一方面,超介質吸波材料的實驗測試方法主要為自用空間測試法,這種測試方法首先需制備大尺寸的測試樣品,并采用兩個喇叭天線在微波暗室里測試其反射系數(S11),最后得出超介質吸波材料的吸波率(A=1-|S11|2).這種測試方法的優點為可測試斜入射角以及不同極化角情況下的吸波性能,缺點是所需測試成本較高.2011年,西安電子科技大學李龍等[29]提出了可在矩形波導里測試小尺寸的超介質吸波材料,這種測試方法所需測試樣品尺寸小,測試系統僅需一個波導同軸轉換器以及矩形波導短路器.其缺點為不能測試超介質吸波材料在不同入射角和極化角情況下的吸波特性.但是,對于某些特定的應用環境,如本文要討論的矩形波導匹配終端,采用矩形波導測試方法將具有其重要的研究價值.本文采用矩形波導測試方法,實驗研究4種基于電諧振單元的超介質吸波材料的吸波性能,并分析將其作為矩形波導匹配終端時的各種指標特性.

2 基于電諧振單元的超介質吸波材料實驗研究

2.1 實驗樣品加工及測試系統搭建

本文采用的4種電諧振單元如圖1所示,其中第1種電諧振單元為參考文獻[30]中所提出的樹枝狀諧振單元,第2種至第4種諧振單元為參考文獻[31]中所設計的幾種諧振單元.此4種單元結構均具有高度對稱特性,因此由其構成的吸波材料具有極化不敏感特性.本文直接研究由這4種電諧振單元構成的吸波材料在X波段(8—12 GHz)矩形波導(WR90)中的吸波性能.

首先,根據X波段矩形波導的橫截面尺寸(22.86 mm×10.16 mm)及其工作頻段,采用商用電磁仿真軟件(Ansoft HFSS 14.0)仿真優化本文所討論的4種超介質吸波材料電諧振單元的結構尺寸.仿真模型如圖2(a)所示,超介質吸波材料置于短路矩形波導的末端,矩形波導另一端設置為波端口.為便于實驗測試驗證,本文所采用的介質材料為FR4板材,其相對介電常數εr=4.0,介質損耗角正切值tanδ=0.02.FR4板材厚度0.8 mm,構成吸波材料的金屬諧振單元以及FR4板材另一面的金屬層為0.018 mm的金屬銅(電導率為5.813×107S/m).基于上述材料及結構參數的限制,優化得出在矩形波導里具有近理想吸波特性的4種超介質吸波材料諧振單元尺寸(如圖1中第二列所示,圖中尺寸單位為mm).根據仿真優化得出的結構參數值,采用電路板刻蝕加工技術,制作出了如圖1中第三列所示的4種超介質吸波材料樣品.其中,第1種超介質吸波材料諧振單元間間隔為7.5 mm,第2及第3種諧振單元間間隔為5.0 mm,第4種諧振單元間間隔為4.8 mm.

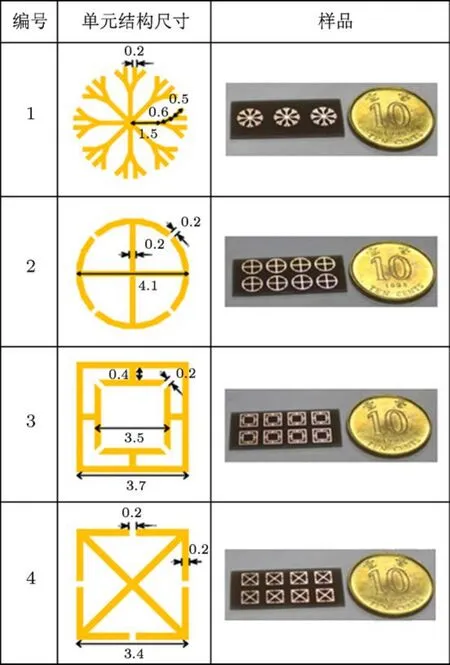
圖1 4種超介質吸波材料電諧振單元示意圖和仿真優化出的結構參數值,以及制備出的對應超介質吸波材料樣品

為測試超介質吸波材料在矩形波導里的吸波性能,本文采用一個工作于X波段的波導同軸轉換器、一個短路器以及安捷倫矢量網絡分析儀(Agilent N5230A)以搭建測試系統(如圖2(b)所示).首先將超介質吸波材料樣品置于波導同軸轉換器的波導端口處,然后將短路器覆蓋在波導端口處以防止電磁波能量泄漏,影響測試結果.最后將波導同軸轉換器的同軸端口與矢量網絡分析儀連接,測試其反射系數.

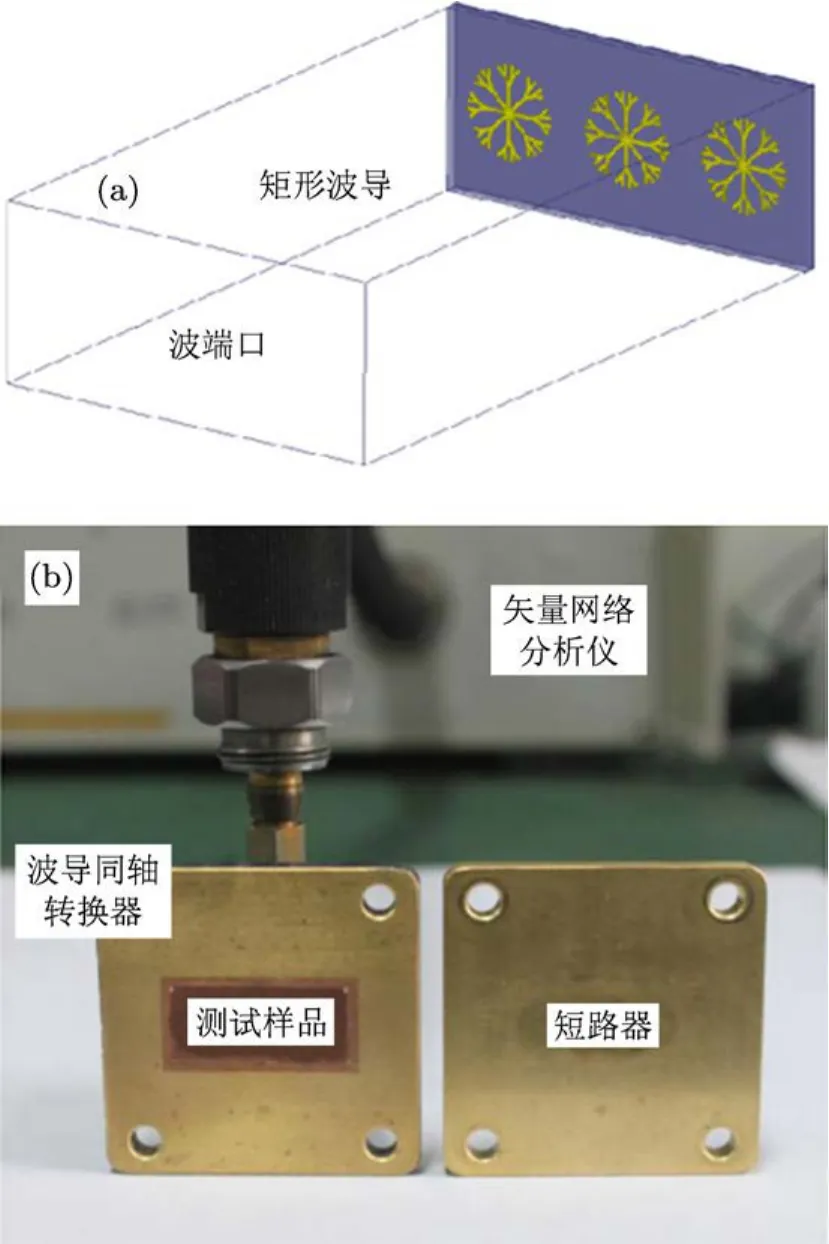
圖2 置于矩形波導里的超介質吸波材料仿真及測試系統 (a)仿真模型;(b)測試系統

2.2 實驗結果分析

采用上述測試系統,分別對本文所討論的4種超介質吸波材料在矩形波導里的吸波性能進行測試,測試結果與相應仿真優化得出的數值結果如圖3所示.其中反射率計算公式為為仿真/測試得出的反射系數值;由于在仿真及測試過程中,波導同軸轉換器的波導端口被短路,因此沒有電磁波能量泄漏,從而得出吸波率計算公式為A(ω)=1-R(ω)=1-|S11|2.由圖3可知,本文所討論的4種超介質吸波材料在矩形波導里均顯示出了近理想的吸波性能.圖3(a)所示為基于樹枝狀電諧振單元的超介質吸波材料的吸波特性,測試結果顯示該種結構吸波材料的吸波峰值為99.4%(10.84 GHz),仿真所得吸波峰值為99.7%(10.68 GHz).測試與仿真所得吸波峰值基本符合,吸波峰值頻率有一定頻率偏移,由分析可知,該頻移為實際加工誤差所致.圖3中其余3種結構超介質吸波材料的測試與仿真結果顯示了相似的特性,此3種吸波材料的測試吸波峰值分別為97.3%(10.77 GHz),96.0%(10.51 GHz),97.2%(11.05 GHz);仿真所得結果分別為99.6%(10.69 GHz),93.8%(10.62 GHz),96.5%(10.95 GHz).

圖3 本文所討論的4種超介質吸波材料在矩形波導里的反射率及吸波率結果 (a)第1種吸波材料;(b)第2種吸波材料;(c)第3種吸波材料;(d)第4種吸波材料

圖4所示為本文所討論的4種超介質吸波材料的電諧振單元以及介質另一面的金屬平板在吸收峰值頻點處的表面電流分布仿真結果.由圖可知,在矩形波導里實現的超介質吸波材料的表面電流分布與其在自由空間中的結果[30]類似.例如,圖4(a)中的樹枝狀諧振結構的表面電流分布滿足軸對稱特性,因此能夠實現典型的電諧振特性;而金屬平板上面的表面電流與樹枝狀諧振結構的表面電流呈反對稱特性,因此能在金屬諧振環和金屬平板之間形成磁諧振特性,此種諧振特點與文獻[30]中分析的一致.圖4中其余3種超介質吸波材料的表面電流特性與第一種結構類似.

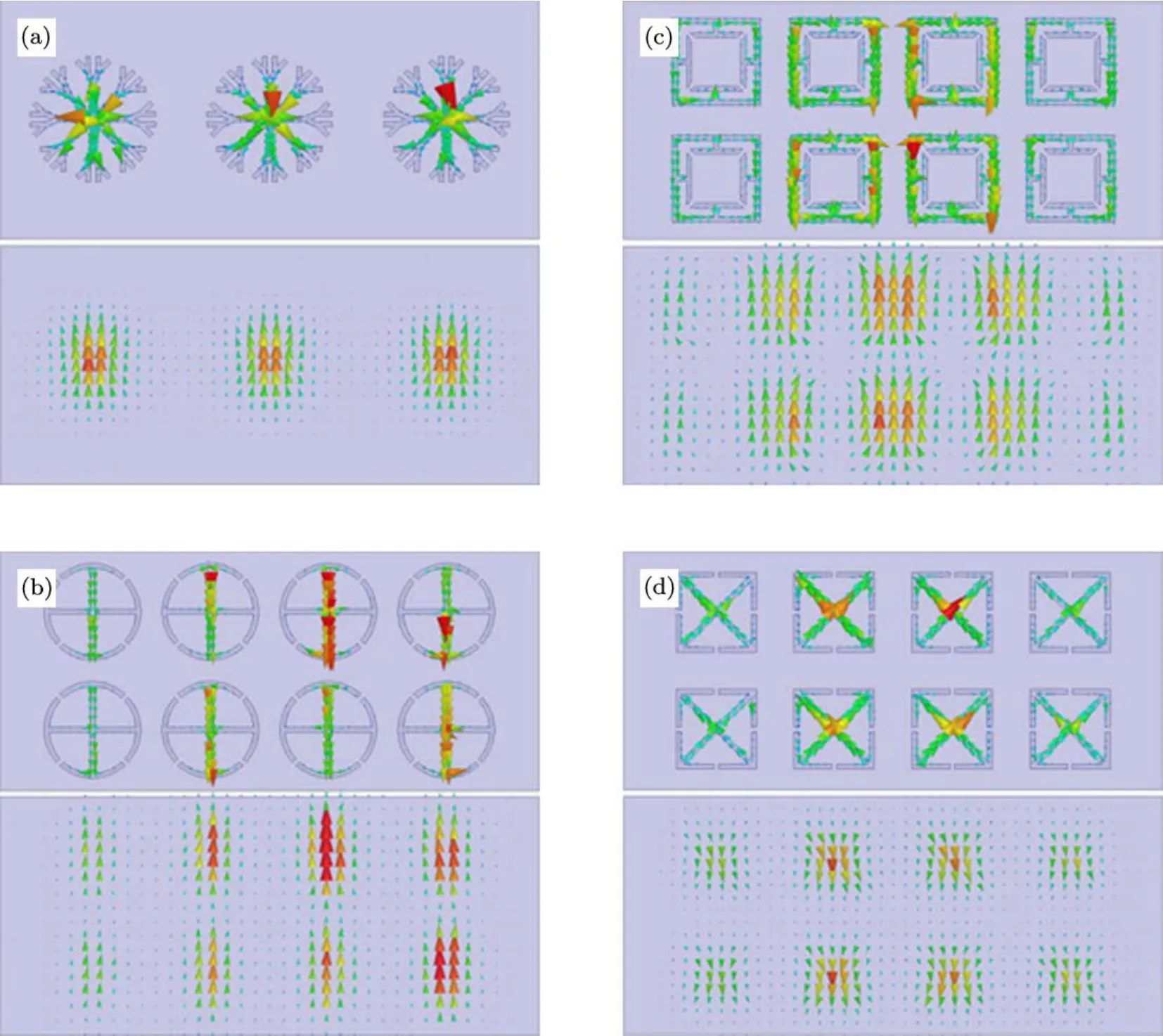
圖4 本文所討論的4種超介質吸波材料的金屬諧振單元以及介質另一面金屬平板上的表面電流分布特性 (a)第1種吸波材料;(b)第2種吸波材料;(c)第3種吸波材料;(d)第4種吸波材料

由此可知,本文所討論的在矩形波導里實現的4種超介質吸波材料具有與其在自由空間中相似的近理想吸波性能.因此,此種矩形波導測試研究方法可適用于其他已經提出的各種結構微波頻段超介質吸波材料,以及可用于實驗測試驗證新提出的各種微波頻段超介質吸波材料的吸波性能.

3 基于超介質吸波材料的匹配終端應用研究

由上一節分析可知,矩形波導加載超介質吸波材料可以實現一定帶寬的吸波作用,且該種結構的反射系數趨近于零,因此,可將這種結構用于設計矩形波導匹配終端(其基本結構如圖2(a)所示),以實現近完美的阻抗匹配特性.本文基于對加載超介質吸波材料的矩形波導的實驗測試及仿真研究結果,得出所討論的4種結構的電壓駐波比特性以及阻抗Smith圓圖特性如圖5所示.由圖可知,第1種及第2種超介質吸波材料加載的矩形波導匹配終端的電壓駐波比特性在相應頻段內顯示出了較好的匹配特性,第3種超介質吸波材料加載的矩形波導匹配終端在其吸波工作頻段內未能很好地達到匹配,第4種超介質吸波材料加載的矩形波導匹配終端表現出一定的匹配帶寬.該4種超介質吸波材料加載的矩形波導匹配終端的最佳匹配點VSWR值,VSWR≤1.5的工作頻段如表1所示,其中第2列及第3列為測試結果,第4列及第5列為相應的仿真結果.為進一步優化矩形波導匹配終端的匹配性能,可通過簡單地調節介質基板的厚度來實現,其調節優化方法類似于吸波材料的優化方法[28].因此,本文所討論的4種超介質吸波材料完全可用于設計矩形波導匹配終端,達到近理想的阻抗匹配性能.為進一步展寬此種匹配終端的工作帶寬,可簡單地通過加載寬帶超介質吸波材料[32]實現.

圖5 4種超介質吸波材料加載的矩形波導匹配終端的電壓駐波比(VSWR)以及阻抗Smith圓圖特性

表1 4種超介質吸波材料加載的矩形波導匹配終端的測試與仿真結果

4 結論

本文采用矩形波導測試系統,實驗與仿真相結合研究了4種超介質吸波材料的吸波性能及吸波機理.結果顯示,超介質吸波材料在矩形波導中的吸波性能及吸波機理與自由空間中類似,因此得出矩形波導測試系統可用于其他新型超介質吸波材料的實驗研究.進一步討論了將超介質吸波材料加載到終端短路的矩形波導中,以實現窄帶的匹配終端應用,結果顯示該種新型的矩形波導匹配終端具有近理想的匹配性能,且其阻抗匹配帶寬可通過設計寬帶超介質吸波材料展寬.本文所討論的超介質吸波材料測試方法及其矩形波導匹配終端應用具有重要的應用前景,可實現寬帶小型化高性能的阻抗匹配終端.

[1]Veselago V G 1968 Sov.Phys.Usp.10 509

[2]Smith D R,Padilla W J,Vier D C,Nemat-Nasser SC,Schultz S 2000 Phys.Rev.Lett.84 4184

[3]Pendry JB 2000 Phys.Rev.Lett.85 3966

[4]Shelby RA,Smith D R,Schultz S 2001 Science 292 77

[5]Chen CH,Qu SB,Wang JF,Ma F,Wang X H,Xu Z 2011 Chin.Phys.B 20 034101

[6]Yang Y M,Wang JF,Xia S,Bai P,Li Z,Wang J,Xu Z,Qu SB 2011 Chin.Phys.B 20 014101

[7]Lu W B,Ji Z F 2011 Chin.Phys.B 20 054101

[8]Li J,Yang FQ,Wang Z,Dong JF 2011 Acta Phys.Sin.60 114101(in Chinese)[李杰,楊方清,王戰,董建峰2011物理學報60 114101]

[9]Zhong J,Huang Y,Wen G,Sun H,Gordon O,Zhu W 2012 IEEE Antenn.Wireless Propag.Lett.11 803

[10]Huang Y J,Wen GJ,Li TQ,Li L W,Xie K 2012 IEEEAntenn.Wireless Propag.Lett.11 264

[11]Zang Y Z,He M X,Gu JQ,Tian Z,Han JG 2012 Chin.Phys.B 21 117802

[12]Xiong H,Hong J S,Jin D L,Zhang Z M 2012 Chin.Phys.B 21 094101

[13]Su Y Y,Gong B Y,Zhao X P 2012 Acta Phys.Sin.61 084102(in Chinese)[蘇妍妍,龔伯儀,趙曉鵬2012物理學報61 084102]

[14]Liu Y H,Liu H,Zhao X P 2012 Acta Phys.Sin.61 084103(in Chinese)[劉亞紅,劉輝,趙曉鵬2012物理學報61 084103]

[15]Xu X H,Xiao SQ,Gan Y H,Fu CF,Wang B Z 2012 Acta Phys.Sin.61 124103(in Chinese)[徐新河,肖紹球,甘月紅,付崇芳,王秉中2012物理學報61 124103]

[16]Fan J,Sun G Y,Zhu WR 2011 Chin.Phys.B 20 114101

[17]Shi Y L,Zhou Q L,Liu W,Zhao D M,Li L,Zhang CL 2011 Chin.Phys.B 20 094102

[18]Zhou Q L,Shi Y L,Wang A H,Li L,Zhang CL 2012 Chin.Phys.B 21 058701

[19]Chen L T,Cheng Y Z,Nie Y,Gong R Z 2012 Acta Phys.Sin.61 094203(in Chinese)[陳龍天,程用志,聶彥,龔榮洲2012物理學報61 094203]

[20]Gu C,Qu SB,Pei Z B,Xu Z,Liu J,Gu W 2011 Chin.Phys.B 20 017801

[21]Gu C,Qu SB,Pei Z B,Xu Z 2011 Chin.Phys.B 20 037801

[22]Zhu W,Huang Y,Rukhlenko I D,Wen G,Premaratne M 2012 Opt.Express20 6616

[23]Yang Y J,Huang Y J,Wen GJ,Zhong JP,Sun H B,Gordon O 2012 Chin.Phys.B 21 038501

[24]Huang Y J,Wen G J,Li J,Zhong JP,Wang PSun Y H,Gordon O,Zhu WR 2012 Chin.Phys.B 21 117801

[25]Zhu W,Premaratne M,Huang Y 2012 J Electromag Waves Appl.26 2315

[26]Xu H X,Wang G M,Liang JG,Peng Q 2012 Acta Phys.Sin.61 074101(in Chinese)[許河秀,王光明,梁建剛,彭清2012物理學報61 074101]

[27]Landy N I,Sajuyigbe S,Mock JJ,Smith D R,Padilla WJ2008 Phys.Rev.Lett.100 207402

[28]Watts CM,Liu X,Padilla WJ2012 Adv.Mater.24 OP98

[29]Li L,Yang Y,Liang C 2011 J.Appl.Phys.110 063802

[30]Zhu W,Zhao X 2009 J.Opt.Soc.Am.B 26 2382

[31]Padilla WJ,Aronsson M T,Highstrete C,Lee M,Taylor A J,Averitt RD 2007 Phys.Rev.B 75 041102

[32]Ding F,Cui Y,Ge X,Jin X,He S 2012 Appl.Phys.Lett.100 103506