大型數控銑齒機振動測試及減振方案研究*

董維新 胡萬良 李云霞

(陜西秦川機械發展股份有限公司，陜西寶雞 721009)

大型數控銑齒機是在傳統的銑齒機基礎上發展起來的，作為大型、高速、高精度的數控機床，其工作性能指標要求也大大提高.比如，作為一臺自動化的機床，為了保證機床在各種工況下的加工穩定性，不僅要求機床結構具有良好的靜態特性，而且更要具有良好的動態特性。

國內外學者針對機械結構的靜動態設計進行了廣泛深入的研究，取得了大量的成果［1－9］。例如，早在上世紀80 年代初，Cleek，A.L.和 Pacelic，V.對數控加工中心進行了結構頻率響應以及模態分析，總結出機床的動態特性是決定其結構性能的重要因素，利用測量裝置得出了系統的頻率響應特性和振型。

本文針對某大型數控銑齒機動態性能、提高加工精度等問題，參考國內外相關研究方法，考察其在實際切削過程中，面臨各種外界干擾以及靜態或動態力的作用下，機床將會出現哪些振動響應，是否影響加工精度，是否影響到切削加工無法繼續進行，繼而進行進一步的動力學分析，看是否可以找到其成因，為提高機床整體動態性能，減小振動提供依據。

1 振動測試方案

機床加工中出現的振動按原因可分為自由振動、受迫振動、自激振動3種［9－11］。對于精密機床，應在保證加工質量的前提下考慮切削效率;相反，對于粗加工機床，應在保證切削效率的前提下考慮加工質量;對于普通機床以及目前正在發展的粗精加工都能使用的機床，應兩者兼顧。切削過程中的振動較為復雜，是各種振動因素的疊加。因此，對機械系統進行振動測試，找出響應振源并改進機械振動系統，可以達到減振提高加工質量的目的。

如圖1所示，對機床進行切削振動測試，可以判別出振動的類型。首先對機床停止時的外界干擾引起的振動進行測量，再測出空轉時的振動。對于頻率與各旋轉件的轉速有關的振動，就可以認為是其中的受迫振動。對于頻率與轉速無關而與機床各零、部件的固有頻率有關的振動，就可認為是其中的自激振動。

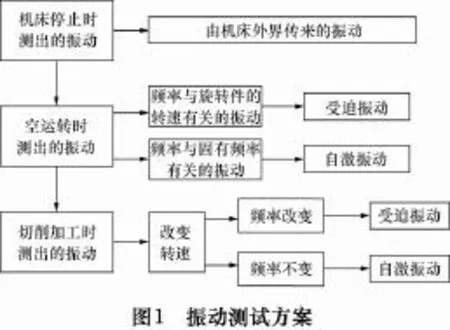
2 切削試驗

圖2為數控銑齒機整機裝配圖，為找出切削加工中各振動量的大小及振源，分別對各轉速調試過程中的銑齒機進行了停機測試試驗、空轉試驗以及切削試驗。測試的重點是刀架系統，因為它是加工系統的最主要部分，其與工件直接接觸，最終影響加工精度。刀架雙擺結構的測點布置如圖3所示。

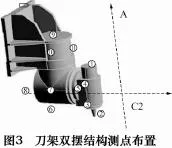
機床雙擺結構為多軸聯動結構，為詳細測試出雙擺結構各個部分的振動量大小以找出主要振動來源，在每個部件上X、Y、Z方向上均布置傳感器。測試系統中單向傳感器11個(布置于雙擺上)，三向傳感器1個(布置于工件正對切削位置)，共占用14個通道。現場測試模型如圖4所示。

按測點號連接好傳感器和儀器，根據靈敏度及增益標定各個通道后。進行采樣示波，調整各通道輸入輸出的增益大小，使信號不致過大超過量程或過小，以防有效信號分辨率低。根據理論分析得到的前六階固有頻率的頻率范圍，設定分析頻率為500 Hz。

2.1 停機測試

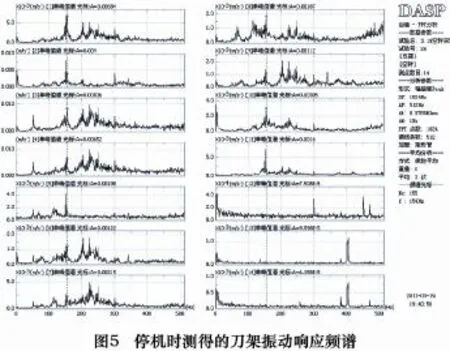
進行停機測試試驗可以找出機床的外部振源，例如經過地基傳來的振動、電磁干擾等。可以引起的振動形式有自由振動和受迫振動。首先采集時域信號，為分析其中各振動頻率分布，對時域信號作自譜分析，得到響應頻譜，如圖5所示。

由圖5響應頻譜可以看出，臺面響應較小。Y、Z方向在512 Hz內加速度響應幅值均在1×10－3m/s2以下，X方向則在4×10－3m/s2以下。而雙擺結構上各測點的幅頻特性曲線基本相近，響應幅值較大的3、4兩測點加速度幅值范圍在1×10－2m/s2以下。

由a=ω2x=(2πf)2x可得到由加速度到振動位移變換公式

式中:a為加速度;f為頻率;w為角頻率。

雙擺上測點出現明顯50 Hz峰值，分析其為交流電電磁力干擾。在3號測點出現最大峰值加速度0.006 m/s2，由式(1)計算出對應振動位移量6.09×10－5mm，振動位移很小。50 Hz以后出現不規則寬頻激勵，振動位移相比50 Hz時更小。綜上可得出結論:外界干擾引起的振動量很小。

2.2 空運轉試驗

根據對機床振動類型的分析，該機床采用電主軸直接驅動刀具進行切削，排除傳動鏈產生的振動。進行空轉試驗主要目的是為了測試出各種受迫振動振源的影響，受迫振動的可能因素有回轉件的不平衡及空轉啟動中外部動力源，例如液壓、氣壓系統引起的交變力等。

測試過程中氣壓驅動裝置仍打開，采用同樣的測點布置方案。精切加工轉速為250 r/min。得到時域信號如圖6所示。

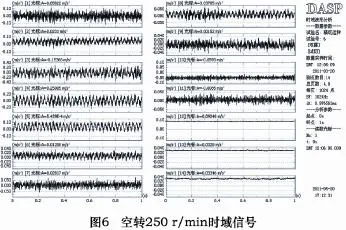
空運轉測試時，工件及臺面不受轉速的影響，其響應同停機時一樣。由時域信號可以看出，仍舊是3、4測點響應加速度值最大。對其進行頻域內自譜分析得到峰值頻率分布。由空轉頻譜可見在停機狀態下的電磁干擾被湮沒，也說明外界干擾相較自身轉速激勵而言可以忽略。雙擺結構測點上具有明顯的峰值響應，在3、4測點響應峰值相對較大。為詳細分析各振動頻率分量，對實驗結果進行了自譜分析，如圖7所示。

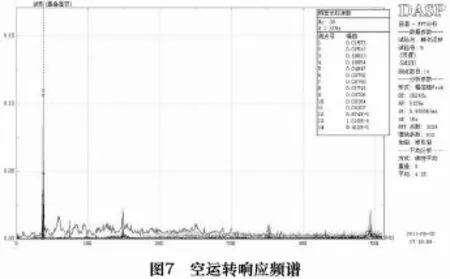
由頻譜分析可以看出各測點具有相似的峰值頻率，說明了測試的可靠性。其中靠近切削刀具的3號測點相較其他測點峰值更大，提取其頻譜峰值加速度數據并按公式(1)計算得到其振動位移量見表1。

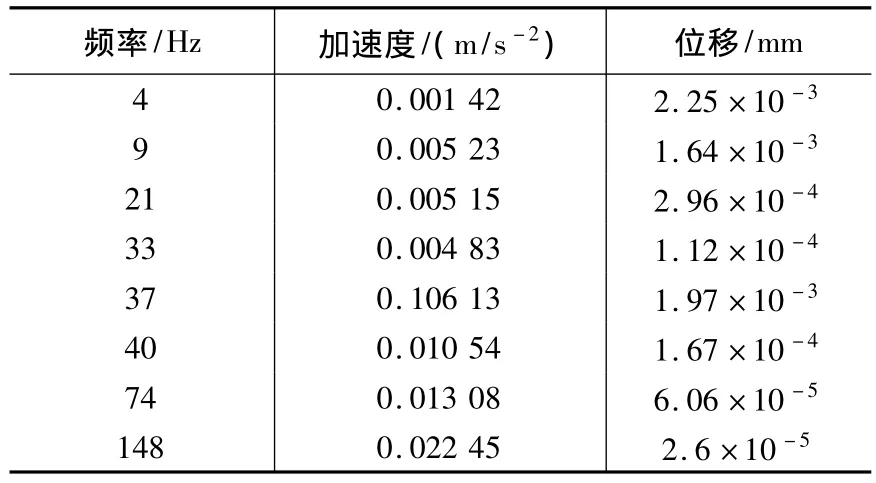
表1 空轉轉速250 r/min下振動頻率及位移

由數據處理結果可見振動位移量最大值為頻率4 Hz，位移大小為2.25×10－3mm。空轉轉速250 r/min對應頻率為4.16 Hz，因數據分析頻率分辨率為1 Hz，有理由認為4 Hz下的振動即為不平衡質量引起的受迫振動。且轉速的微小跳動，其后的9 Hz可看作轉速頻率2倍頻，且21 Hz、33Hz等都與轉速頻率有倍數關系。可進一步得出結論:振動來源于主軸系統不平衡引起的受迫振動。

2.3 切削試驗

切削過程中采用氣動驅動，主軸變頻器在切削轉速250 r/min下頻率為12.5 Hz。測試時采用銑削加工，常用進給量為50 mm/min。銑削切屑刀片數為4，據轉速得刀具斷續切削引起的激勵頻率為16.67 Hz。

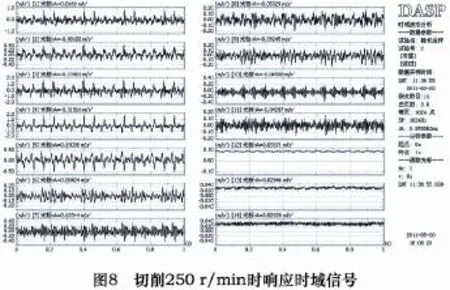
選取試驗號2的時域信號進行分析，如圖8所示。可以看出，相比停機和空轉時響應加速度值明顯提高很多。且臺面振動響應也有所提高，相比雙擺結構上的測點而言響應仍較小。同前一樣，3、4號測點響應加速度值最大。振動加速度范圍為±2 m/s2，其他測點在±1 m/s2以內。

為得出具體峰值頻率分布，對其進行自譜分析，如圖9所示。由全部14個通道分析結果可以明顯看出各頻譜具有很好的相似性，說明了測試結果的可靠性。臺面和雙擺結構上測點也具有基本相同的峰值分布，可見在切削加工時雙擺部分和臺面部分相互作用，各結構部件組成切削系統。

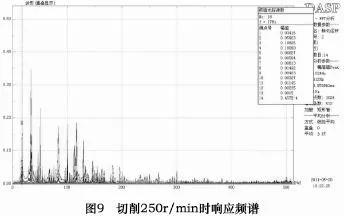
頻譜中出現明顯的峰值頻率，且14個通道測點的頻譜中的峰值頻率分布基本一致。對比發現，臺面峰值響應相對雙擺結構上的響應差3個數量級，相比雙擺小得多。

切削試切過程中，在加工小曲率位置時進給量為50 mm/min，而在加工齒輪曲面拐點也即大曲率圓弧時為了切除較多材料進給量設定為68 mm/min。且現場可明顯感覺到在加工大曲率圓弧時振動大。因此有必要對兩數據進行對比分析，每組試驗中均是3號測點響應峰值最大，2號試驗為加工小曲率半徑，對其進行數據處理，得到位移響應頻率分布。

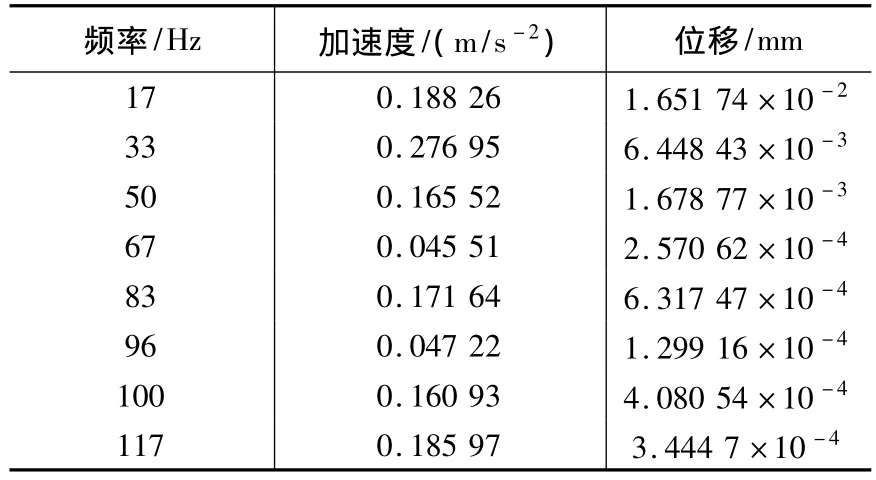
表2 加工小曲率位置振動頻率及位移

由數據處理結果可以看出，位移最大幅值出現在17 Hz，切削激勵頻率。位移值為1.651 7×10－2。比空轉時的振動位移高出一個數量級。其后出現的33 Hz、50 Hz為切削激勵頻率的倍頻，振動位移與比17 Hz時低一個數量級。5號試驗為加工大曲率半徑，對其進行數據處理作對比分析，如表3所示。

由加工大曲率半徑位置的分析結果，最大位移響應出現在16 Hz。因頻率分辨率為1 Hz，且轉速跳動的原因，仍可認為其為切削激勵頻率。在2倍頻32 Hz的振動位移量也很大，在同一數量級。其后的倍頻下振動位移則相對較小。

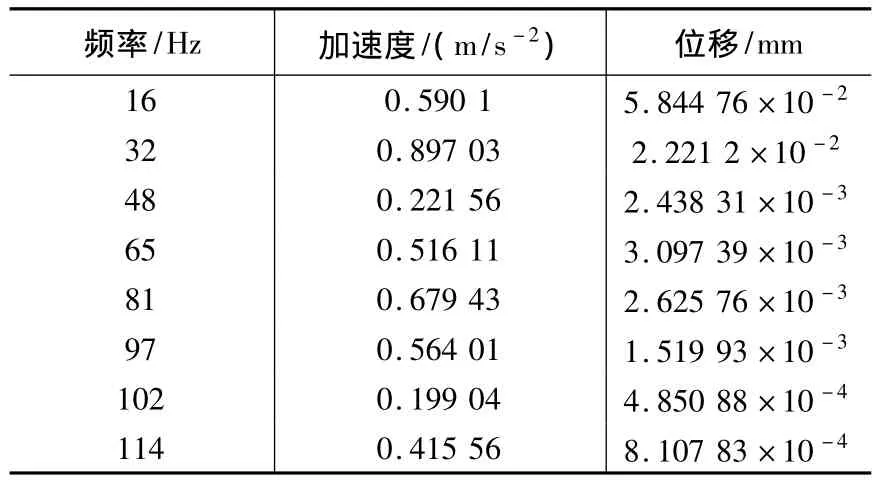
表3 加工大曲率位置振動頻率及位移

3 試驗結果分析

3.1 振動測試結論

在以上停機試驗、空轉試驗及切削試驗所有測試中均是3、4號測點振動位移最大，且兩者加速度傳感器方向同向。該兩個測點對應的是刀架的最前端，刀架作為懸臂結構，該兩個測點正好對應其最前端，同時也是最接近刀具加工區的位置。對比兩者切削時域信號對比圖如圖10所示。

由時域信號可見3、4號測點出現明顯峰值響應的頻率基本是相同的。對比振動相位，既有同相位峰值也有相差180°左右的峰值，也即兩測點有時同向達到最大位置，有時同時反向達到最大位移。由此判定電主軸部分的運動為既有平動，又有繞C2軸的扭轉，因此對加工精度有很大影響。

如圖11所示，對比各個頻率下的不同工況振動位移量，在增大進給量加工大曲率位置時振動位移最大，是加工小曲率位置時振動位移的兩倍以上，且兩者的最大振動位移均出現在切削激勵頻率下。由空轉振動幅值頻率可以看出，主軸系統本身存在不平衡問題，但引起的受迫振動位移相對較小。

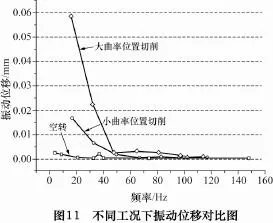
由測試結果可得出結論:外界干擾引起的振動很小;切削中工件未出現明顯振紋，排除顫振的因素;根據前面對立柱部分的固有頻率分析結果，說明切削激勵頻率在結構固有頻率共振區外，綜上也說明了切削系統設計的合理性;回轉件不平衡引起的受迫振動相比切削激勵引起的振動小;切削試驗中產生的振動主要為切削激勵下的受迫振動。

3.2 減振方案分析

根據上述分析，因主軸系統不平衡引起的振動幅值很小。影響較大的因素是切削刀具安裝所出現的不平衡問題。可以通過重新調整安裝來減小這一因素引起的振動量。

減小因斷續切削激勵引起的受迫振動的方法有:(1)改善結構設計，增大切削系統剛度;(2)設計隔振裝置，提高系統結構等效阻尼;(3)提高切削轉速或減小切削進給量，以減小切削力;(4)或改善加工工藝，改變切削力方向使其避開結構剛度薄弱方向。

對于前兩種方案，對結構進行重新設計或增加隔振器，就要增加一定的生產成本，而且相關動力系統也需作相應改變。第三種方案中提高切削轉速使刀具材料需要作相應的改變，也會一定程度上提高成本，而減小切削進給量必將影響加工效率。由于機床雙擺結構可實現多軸聯動，可通過軟件程序調整加工各軸相對位置，對已在進行加工的機床，此該方案較為可行。

4 結語

本文分析了機床振動的形式。為找出振動來源，對機床切削過程分別進行了和切削試驗。停機測試及空轉實驗結果表明外界干擾較小，在進行了切削試驗后發現主軸系統存在不平衡問題，經過分析發現振動主要來源于主要振動來源于切削激勵頻率引起的受迫振動。在整個切削過程未出現明顯振紋，從而可以排除顫振的因素，進一步說明了切削系統設計的合理性。在得到測試結果并對其進行分析的基礎上，本文還提出了幾種減振方案，并對方案進行了分析，為以后機床的振動控制提供了一定的依據。

［1］張波，陳天寧，虎恩典，等.數控車床分體式床身結合面參數優化識別及其動特性分析［J］.現代制造工程，2004(6).

［2］董凱夫.MK7132A數控臥軸矩臺平面磨床的試驗模態分析［D］.杭州:浙江工業大學，2008.

［3］大久保信行.機械模態分析［M］.上海:上海交通大學出版社，1985.

［4］大久保信行.模態分析發展綜述［J］.機械研究，1985(1).

［5］李濤.MB4250－高精度立式桁磨機床的動態特性分析［D］.上海:上海交通大學，2008.

［6］Zaghbani I，Songmene V.Estimation of machine－tool dynamic parameters during machining operation through operational modal analysis［J］.International Journal of Machine Tools and Manufacture，2009，49(12 －13):947–957.

［7］Jiang T CM A.System approach to structural topology optimization:designing optimal connections［J］.Journal of Mechanical Design，1998，(12):619－621.

［8］Myers A.Finite element analysis of the structural dynamics of a vertical milling machine［M］.Laser Metrology and Machine Performance VI.WIT Press，Southampton，2003:431 －440.

［9］楊嘯，唐恒齡，廖伯瑜.機床動力學(Ⅰ)［M］.北京:機械工業出版社，1993:110－115.

［10］楊嘯，唐恒齡，廖伯瑜.機床動力學(Ⅱ)［M］.北京:機械工業出版社，1993:1－98.

［11］廖伯瑜，周新民，尹志宏.現代機械動力學及其工程應用——建模、分析、仿真、修改、控制、優化［M］.北京:機械工業出版社.2004.