基于統計過程控制的刀具狀態實時監控策略的研究

劉曉東 張秀峰 張 鶴 唐俊杰

(同濟大學機械與能源工程學院，上海 201804)

在刀具狀態實時監控策略的研究中，隨著檢測方法和信息處理技術的迅速發展，目前已經取得了一定的研究成果。以小波分析為主的時頻分析技術能同時在時域和頻域上對信號進行局部分析，但無法有效處理切削加工過程中存在諸多不確定偶然因素以及各頻段信號干擾問題［1］;而新興的神經網絡等計算機智能技術，也存在著實現比較復雜、成本較高、難以實用化等問題。

因此，本文提出了將統計學思想引入刀具狀態實時監控系統，并運用統計過程控制技術對銑削過程的刀具狀態進行實時監控。在應用Holt－Winters指數平滑預測模型以及改進EWMA控制圖作為主要監控策略的基礎上，提出了基于原始觀測數據和基于互相關系數為特征量的兩種監控策略。并使用銑削試驗數據，對兩種監控策略進行監控效果分析。

1 Holt－Winters指數平滑預測

Holt－Winters指數平滑預測方法是一種基于觀測數據的預測方法，而銑削試驗中切削力信號具有雙季節性成分，分別為主軸旋轉周期T和刀齒周期T/n，其中n為銑刀刀齒數，具有雙季節性數據序列的Holt－Winters加法模型由水平平滑公式、趨勢平滑公式、兩季節平滑公式和整體平滑公式組成，可表示為:

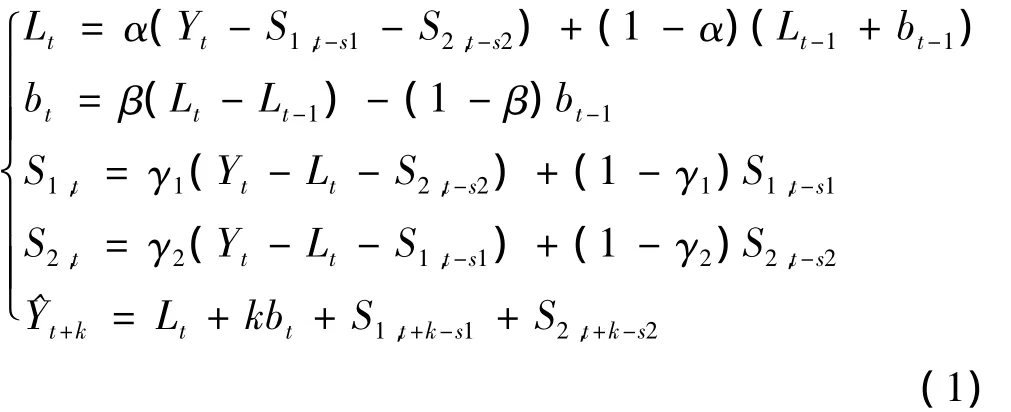
式中:Lt表示銑削力信號中的水平成分;bt表示趨勢成分;S1，t和 S2，t分別表示為兩個季節性成分;Yt為銑削力信號觀測值;^Yt+k則表示為觀測值的超前k步預測;α、β、γ分別是模型的指數平滑系數，其區間為［0，1］［2］。

由式(1)可知，在建立切削力預測模型時還必須獲得利用銑削過程中最開始部分的觀測數據進行初始值計算，如式(2)所示。

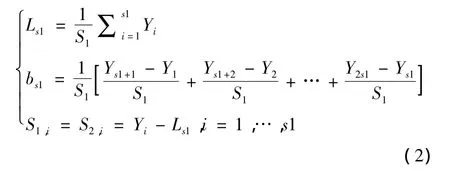
針對銑削過程的切削力預測，為了得到預測模型中的Holt－Winters指數平滑系數，可在RMSE最小的條件下選擇指數平滑系數α、β、γ的最優值，具體如式(3)所示:

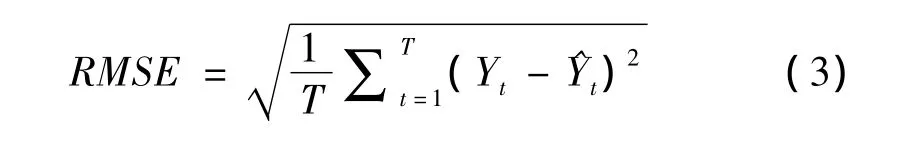
2 改進的EWMA控制圖

實際切削加工過程中的觀測數據并不是總能滿足彼此間統計獨立的假設前提，往往存在一定的數據自相關現象。如果仍然使用以往的常規控制圖進行監控，將會導致大量誤警報的出現，大大降低監控系統的可靠性和精確性。結合銑削過程切削力信號以及Holt－Winters預測模型的特點，本文采用基于原始觀測數據的指數加權滑動平均(EWMA)控制圖，有效解決過程中的數據自相關問題。同時，直接以Holt－Winters預測值作為控制中心線，不需要任何其他形式的建模或統計量計算，使整個過程能在控制圖上動態地呈現出來。改進后EWMA控制圖的上、下控制限的基本形式如下［3］:

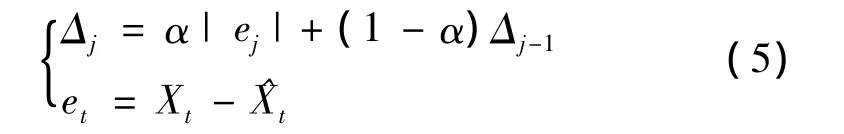
式中:α是第一類錯誤的概率，且0≤α≤1，此處取α=0.001。其中初始值Δ0可用式(6)計算:

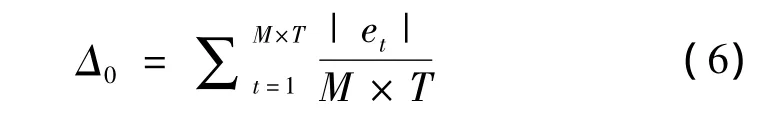
式中:M×T為過程中樣本觀測數據的個數。然后，利用正態分布假設中的關系:≈1.25Δt求得標準差σ的估計值，從而確定控制圖的上、下控制界限［4］。

3 監控策略的應用分析

3.1 切削力信號采集實驗

設計實驗對監控系統進行應用分析。所選擇數控立式銑床最高轉速1 500 r/min，切削速度范圍23.5～1 180 mm/min;銑刀選用以色列ISCAR公司的三齒螺旋槽立銑刀，直徑30 mm;工件材料為普通45號鋼，未經熱處理;切削方式采用順銑。測力裝置采用實驗室自主研發的旋轉式銑削動態測力儀。其中銑削力信號采樣頻率為2 000 Hz，機床主軸轉速為540 r/min。

實驗針對同一材質的加工工件，分別設計兩組不同切削加工參數，具體切削加工參數如表1所示。

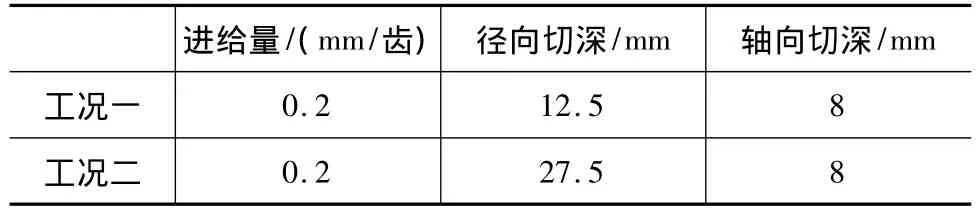
表1 實驗切削參數

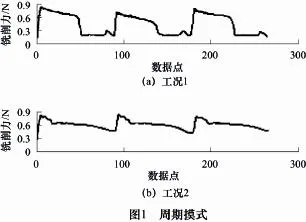
綜合考慮到主軸轉速、采樣頻率等，在每個主軸旋轉周期內取246個數據點，分別得到了兩種不同工況下的銑削力信號，工況1整個銑削過程無任何異常狀態出現，屬于典型的平穩切削加工過程，工況2中被加工工件局部缺陷的存在，使得整個切削過程存在一定程度的波動，表現為切削力信號中某些波峰值出現不同程度的偏大或者偏小，具體的周期模式如圖1所示。由于儀器記錄的電壓值與實際銑削力的大小成線性關系，因此，其電壓值即可表示切削力信號的相對大小，不影響監控系統的應用分析結果。

3.2 監控應用分析

3.2.1 基于原始觀測數據的監控應用

首先將銑削試驗采集到的切削力信號分成兩部分:第一部分由初始穩定階段的前M個信號周期組成，此處取M=20。該部分的信號數據主要是用來確定Holt－Winters預測模型參數α、β、γ以及EWMA控制圖的上、下控制限參數，在線完成銑削過程刀具狀態預測模型和統計控制圖的建立;第二部分即為從第M+1個周期開始的所有信號數據Yj(k)。

當第一階段中的Holt－Winters預測模型參數和EWMA控制圖在線確定后，就可以利用預測模型對銑削力進行超前n步預測，再運用EWMA統計控制圖就可以判斷銑削過程中刀具狀態是否處于統計控制狀態。若處于統計控制狀態，說明銑削過程中刀具無異常狀態發生;若不處于統計控制狀態，則說明過程中出現了異常狀態，此時監控系統會發出預警報，以便操作人員進行進一步的診斷和故障排除。

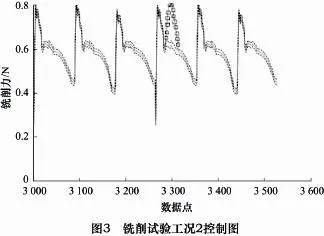
根據上述基于原始觀測數據的刀具狀態監控策略，分別計算得到了兩種工況下銑削力信號的EWMA控制圖。如圖2所示，其中:實線表示銑削力信號原始觀測數據，虛線則表示控制圖的上控制限UCL和下控制限LCL。

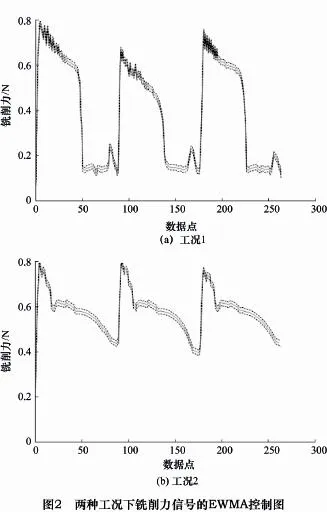
在銑削試驗工況1的統計過程控制圖中沒有連續失控點，表明刀具無任何異常狀態或失效，與真實工況1設定的“平穩切削”情況相吻合。在銑削試驗工況2的控制圖中，如圖3所示出現了較明顯的連續失控點(圖中小圓圈即表示失控點的位置)，表明有間斷性異常狀態發生。而真實工況2設定的“加工工件存在局部缺陷”工況，正好可能導致銑削力信號發生間斷性波動，與監控判斷結果吻合。

3.2.2 基于互相關系數為特征量的監控應用

在切削加工過程中，由于工件及刀具各種偶然因素的存在，如果僅采用上述基于原始觀測數據的刀具狀態監控方法，往往會因無法辨識出其中的偶然波動而發出過多的誤警報，從而降低整個刀具監控系統的監控性能。因此，在充分利用Holt－Winters指數平滑預測模型以及EWMA控制圖優勢的基礎上，有效結合銑削力信號本身所具有的特點，提出了基于銑削力信號互相關系數為特征量的刀具狀態監控方法。

互相關系數是衡量變量之間相關性強弱的重要統計指標，通常用r表示。在具有周期性數據信號的穩定性判斷過程中，互相關系數是其中一類非常敏感的時域特征。對于兩個周期信號z(k)和w(k)，互相關系數表示如下［5］:

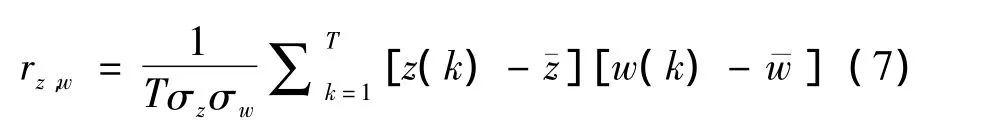
式中:T為信號每一周期中的數據點數;σz、σw分別為z(k)和w(k)的標準差;ˉz、ˉw分別是z(k)和w(k)的時域均值。

同樣，我們需要將銑削試驗采集到的切削力信號分成兩部分:第一部分由采集信號初始階段的前M個信號周期組成，此處取M=20。該部分的信號數據除了用于在線確定Holt－Winters預測模型參數及EWMA控制圖參數外，主要是用來確定參考周期Y*(k)，然后利用此參考周期Y*(k)就可以計算與其余信號周期的互相關系數，進行互相關分析;第二部分即為從第M+1個周期開始的所有信號數據Yj(k)。當第一階段中的參考周期Y*(k)在線確定后，就可以逐一計算與其余信號周期Yj(k)間的互相關系數rj=rY*，Yj，最終形成統計過程分析所需的互相關系數序列{rj}，j=1，2，…，N，其中N為所采集銑削力信號的信號周期個數。

在基于互相關系數作為特征量的刀具狀態統計過程控制中，首先需要將旋轉測力儀采集到的切削力信號以固定長度T劃分成N個連續信號周期。但由于銑削過程中主軸轉速的不穩定性以及主軸周期與采樣周期Ts的整除問題等影響因素，使得劃分后的各信號周期彼此存在相位滯后誤差，從而可能會引起互相關系數計算的誤差。因此，需要利用優化算法對信號周期逐一進行相位誤差調整，如式(8)和(9)所示。

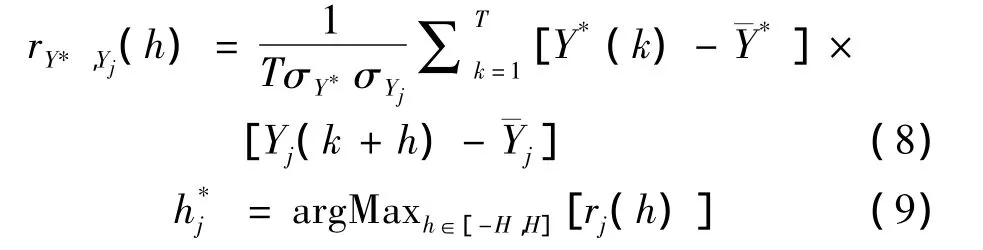
式中:h為Y*(k)與任一信號周期間的相對滑移量，介于［－H，H］范圍內，通過比較分析得出最佳相位調整量。此處，綜合考慮主軸轉速、采樣周期與銑刀齒數，取H=20來保證相位調整中可能出現的問題。

針對銑削試驗兩種工況下采集到的原始切削力信號，分別采用上述監控策略確定了各自的參考信號周期Y*1(k)，Y*2(k)以及Y*3(k)，根據上述基于互相關系數為特征量的刀具狀態監控策略，分別計算得到了這兩種工況下信號周期互相關系數的EWMA控制圖，如圖4。

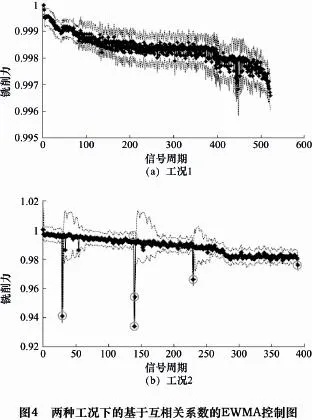
由圖4可以看出，工況1屬于出現了Y1，141(k)和Y1，457(k)兩處不同的統計失控點。但實際情況中，由于工況1屬于正常平穩切削過程，且無任何異常狀態發生，因此可以認為這兩處統計失控點屬于誤判斷，誤警報率為0.35%。在工況2中，共出現了6處統計失控點。其中，Y2，30(k)，Y2，146(k)以及 Y2，231(k)等 3 處失控點均發生在互相關系數驟降至極小點的位置，其余的均處于相關系數序列小幅振蕩區域。上述6處統計失控點均可以找出原因，即因工件材料缺陷而引起的刀具異常狀態，此時監控系統將產生警報。

4 結語

本文應用Holt－Winters指數平滑預測模型以及改進EWMA控制圖作為主要監控策略的基礎上，提出的基于原始觀測數據的刀具監控策略和基于互相關系數為特征量的刀具監控策略。其中，前者通過原始數據直接監測切削狀態，有效減小誤差，但存在著因無法辨識出其中的偶然波動而發出過多誤警報的問題，而后者正好能夠較有效地解決這一問題，從而提高了整個監控系統的監控性能。若將上述兩者有效結合使用，能在一定程度上提高整個監控系統的監控性能，降低誤警報率，提高可靠性。

［1］王細洋，龍亮，郭敏.基于振動信號的刀具狀態監控技術研究［J］.南昌航空大學學報，2011，25(3):42 －47.

［2］張麗，閆世鋒.Holt－Winters方法與ARIMA模型在中國航空旅客運輸量預測中的比較研究［J］.上海工科技術大學學報，2006，20(3):280－283.

［3］常洪江.基于馬爾可夫鏈的EWMA控制圖參數優化及其實現［J］.制造業自動化，2010，32(6):64 －67.

［4］郭彥蘭，崔利榮，張晨宇.統計控制圖的異常判斷準則分析［J］.數理統計與管理，2007，26(3):468 －474.

［5］于英華，徐興強，徐平.以方差和互相關系數判別切削顫振的仿真研究［J］.組合機床與自動化加工技術，2007，16(5):24 －26.