基于IDDT和SVM的混合電路故障診斷探究

潘 強，王懷龍，楊 超

（海軍工程大學電子工程學院，湖北武漢 430033）

0 引言

由于待測數據受限，混合電路實際的故障類型又多樣化，其故障診斷具有特殊性。通過電流測試可以避免混合電路故障診斷時對模擬和數字電路的劃分，應用較廣。動態電流測試（IDDT）通過故障狀態下的瞬態電流與正常狀態相比來判斷故障，能直接反映電路狀態轉換時內部信號變化過程，彌補靜態電流測試（IDDQ）的不足，是混合電路較好的故障特征參數。

支持向量機具有結構簡單、學習速度快、泛化能力強等優點，能解決神經網絡應用中的速度較慢、局部極小值問題，在少樣本、非線性等情況下具有更強的泛化能力，適合在電路故障診斷等有限樣本信息處理時應用。

1 支持向量機的基本原理

支持向量機是建立在統計學習理論VC維和SRM原則上的學習方法，支持向量機能有效解決二分類問題[1]。

支持向量機通過事先選擇的非線性映射（核函數），將輸入空間映射到一個高維的特征空間，在特征空間中構造最優分類超平面(Optimal Hyperplane)[2]。

假設給定的兩類樣本集為（xi，yi），其中i=1，2，…，n，n是樣本總數；xi為輸入向量，diRx∈ ，d表示輸入空間維數；yi代表類別號，yi∈｛-1 ,1 ｝。多維空間的線性判別函數一般表示為

式中的w表示特征空間中分類超平面的系數向量，b表示分類面閾值，最優分類面滿足：wx+b=0。

支持向量機的基本思想可用圖1表示。

圖中實心圓和空心圓分別代表兩類樣本，H為分類超平面，H1、H2分別為過兩類中離分類超平面最近的樣本且平行于分類超平面的超平面，它們之間的距離 稱為分類間隔(margin)[3] [4]。

最優分類超平面就是要求分類超平面不但能夠將兩類樣本正確地分開，而且能夠使兩類樣本的分類間隔最大。前者是保證經驗風險最小，后者則是為了使推廣性的界中的置信范圍最小，進而使真實風險最小。

圖中分類間隔最大同 最小等價，求最優分類面問題轉換為求（2）的最小值問題。

圖1 最優分類面Fig.1 Optimal classified plane

混合電路實際的故障診斷是典型的多故障模式識別問題。在混合電路多故障識別時，需要重新設計支持向量機的分類算法，使之具備多分類能力。

目前，已有多種算法可以將支持向量機推廣到多模式識別問題，這些算法統稱為“多類支持向量機”(Multi-category Support Vector Machines, M-SVM)。常用的算法有三種：1-a-1算法、1-a-r算法、DDAG算法。

2 多類支持向量機算法研究

采用標準樣本Iris數據集（英國著名統計學家R.A.Fisher提出）對支持向量機的常用算法進行研究。Iris數據集描述三種花卉(Setosa, Versicolour, Virginica)，包含了四個基本屬性，即萼片長度、萼片寬度、花瓣長度、花瓣寬度。其中，三種花卉各有50組數據，共150組數據。將其中75組數據用作訓練集，另外75組用于測試集。

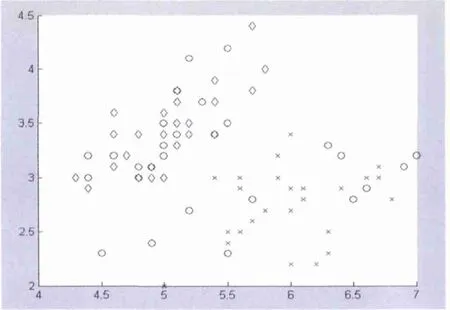
圖2 二維特征樣本分布圖Fig.2 The scatter map of two dimension characteristic samples

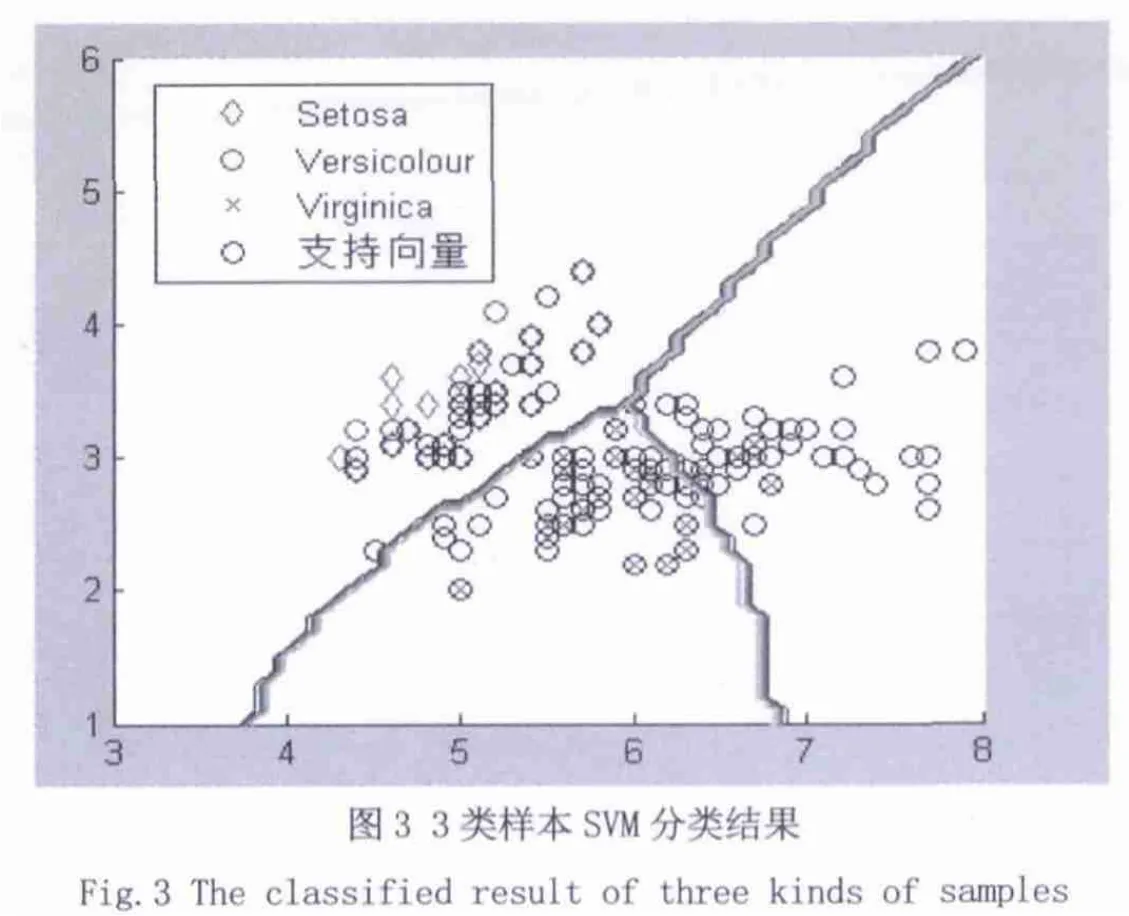
萼片長度、萼片寬度的二維特征樣本可視化如圖2所示。在支持向量機多類分類中，核函數采用高斯徑向基，尋優出的最佳參數對(C, )=(10, 0.5)。為了對比BP神經網絡的分類結果，在仿真過程中采用結構為4-10-3的三層網絡對Iris數據集進行分類，訓練誤差為0.05。3類樣本SVM分類結果如圖3。

對比上述三種常見的支持向量機多類分類算法，尋求應用于混合電路故障診斷的最優算法。

分類結果如表1示。

從表1可以得出如下結論：

(1) 在相同的有限訓練樣本和測試樣本情況下，SVM的分類精度均高于BP神經網絡。同時，訓練時間明顯小于BP神經網絡，表現出更強的分類能力，適用于混合電路的故障診斷。

(2) DDAG算法所需的訓練時間和測試精度均優于1-a-1算法和1-a-r算法，能更加快速而精確地分類識別。

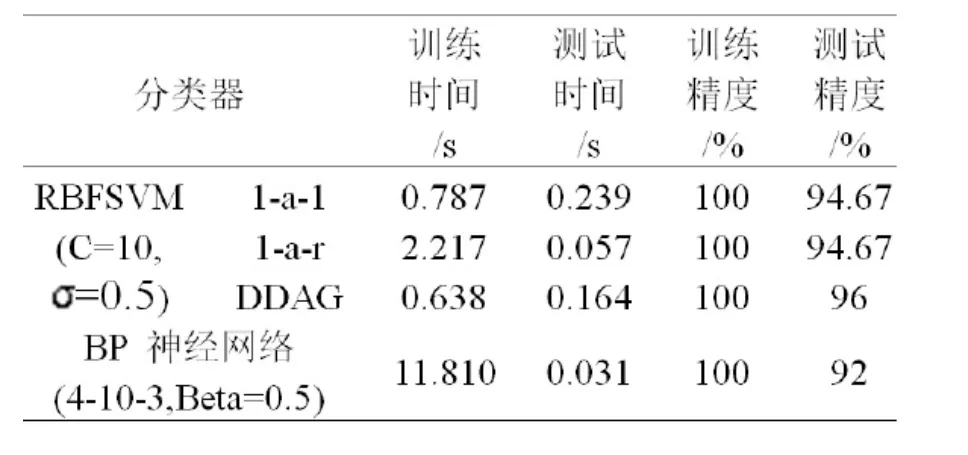
表1 SVM各種算法和BP神經網絡分類結果對比Tab.1 The result of classification contrasted between BP and SVM algorithm

3 RBF核函數參數的確定

核函數及其參數的尋優至關重要,相關文獻研究表明【6】【7】，具有平滑特性的高斯徑向基核函數(RBF)具有很強的學習能力，函數的每一基函數中心對應一個支持向量。同時，輸出權值由算法自動確定。本文采用RBF作為SVM的核函數, SVM的性能主要由核函數參數σ、懲罰因子C和松弛因子γ進行調整。

確定SVM參數，構造最佳分類器是應用的關鍵之一。本文對γ取默認值，采用改進的網絡搜索算法確定(C， )以獲取最佳的故障診斷分類器。

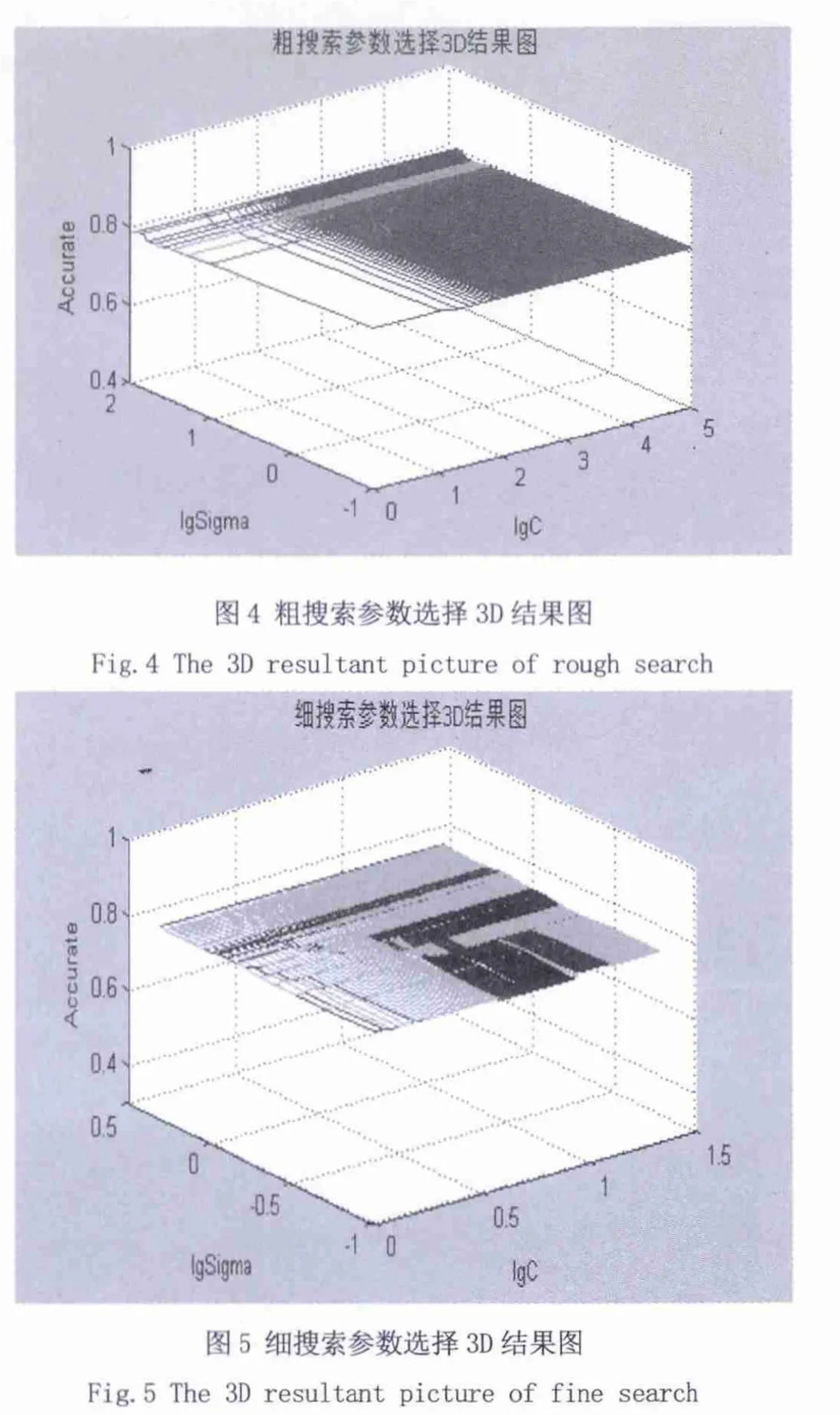
參照上節采用的Iris數據集進行參數尋優。首先，選用步長為10的(C, )組合，如C=(1,10000), =(0.1,100)得到精度最高的(C, )=(11,1.1)，圖4為粗搜索參數選擇3D結果圖。其次，在這兩個值附近的一定范圍內進行更加細致的網絡搜索，如本文選擇C=(1,20)， =(0.1,2)，步長為0.1。最后，通過圖5的細搜索參數選擇3D結果圖，研究得出了本文尋優出的最佳參數對為(10,0.5)。

4 仿真研究與結果 分析

為了對比混合電路的故障診斷率，本文選取555構成的單穩態觸發器作為仿真電路，如圖6所示[7]。

電路無故障情況下50次蒙特卡洛分析的動態電流IDDT曲線圖如7所示。對其 進行5層小波分解，圖8是一次分析的小波分解圖。通過小波分解系數序列求得每種模式下的能量值，表2列出每種模式下的兩個能量特征值。

首先，測試已經學習過的全部訓練樣本20個。然后，用沒有學習過的測試樣本30個測試采用不同算法的支持向量機多故障分類器的推廣能力。由于仿真實驗數據比較多，表3、4只給出了采用DDAG算法的部分重要數據，最終的測試分類結果見表5。

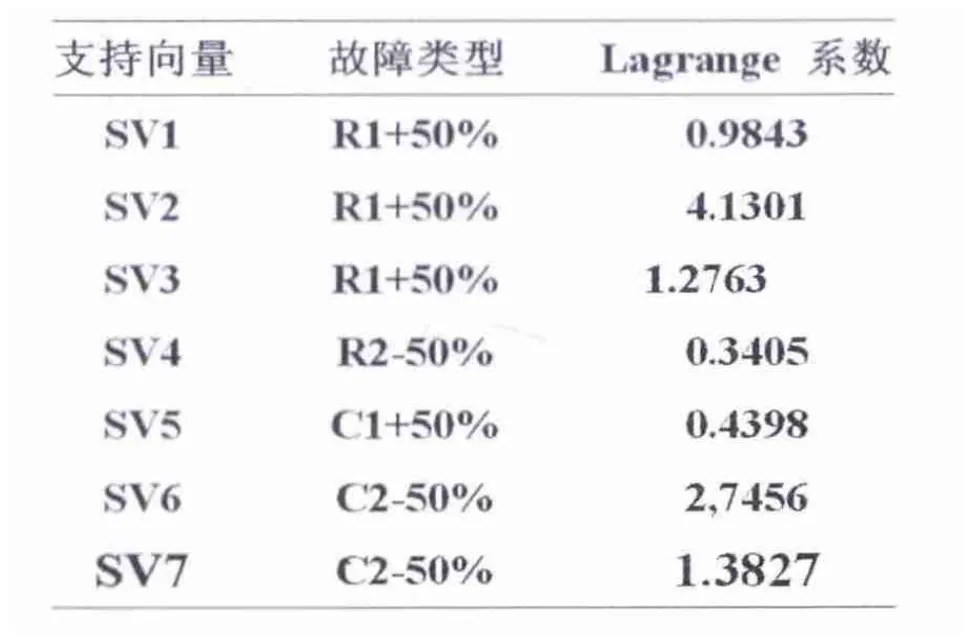
表4 SVM25二分類器的Lagrange系數Tab.4 The Lagrange coefficient of SVM25 two class classification

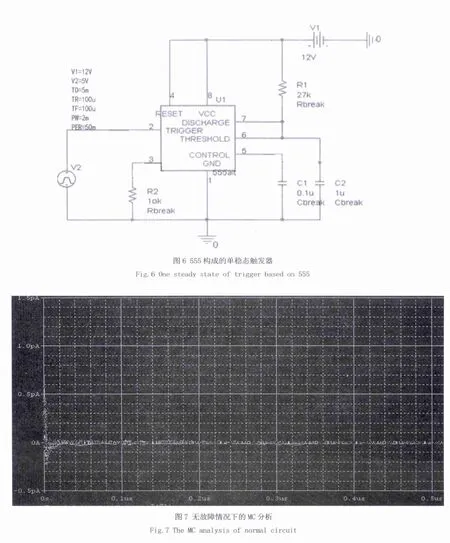
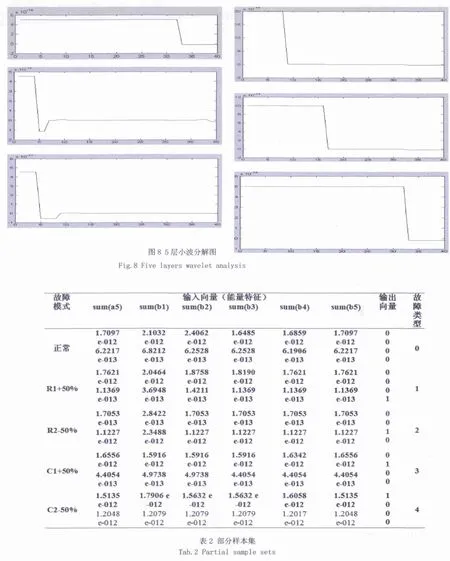
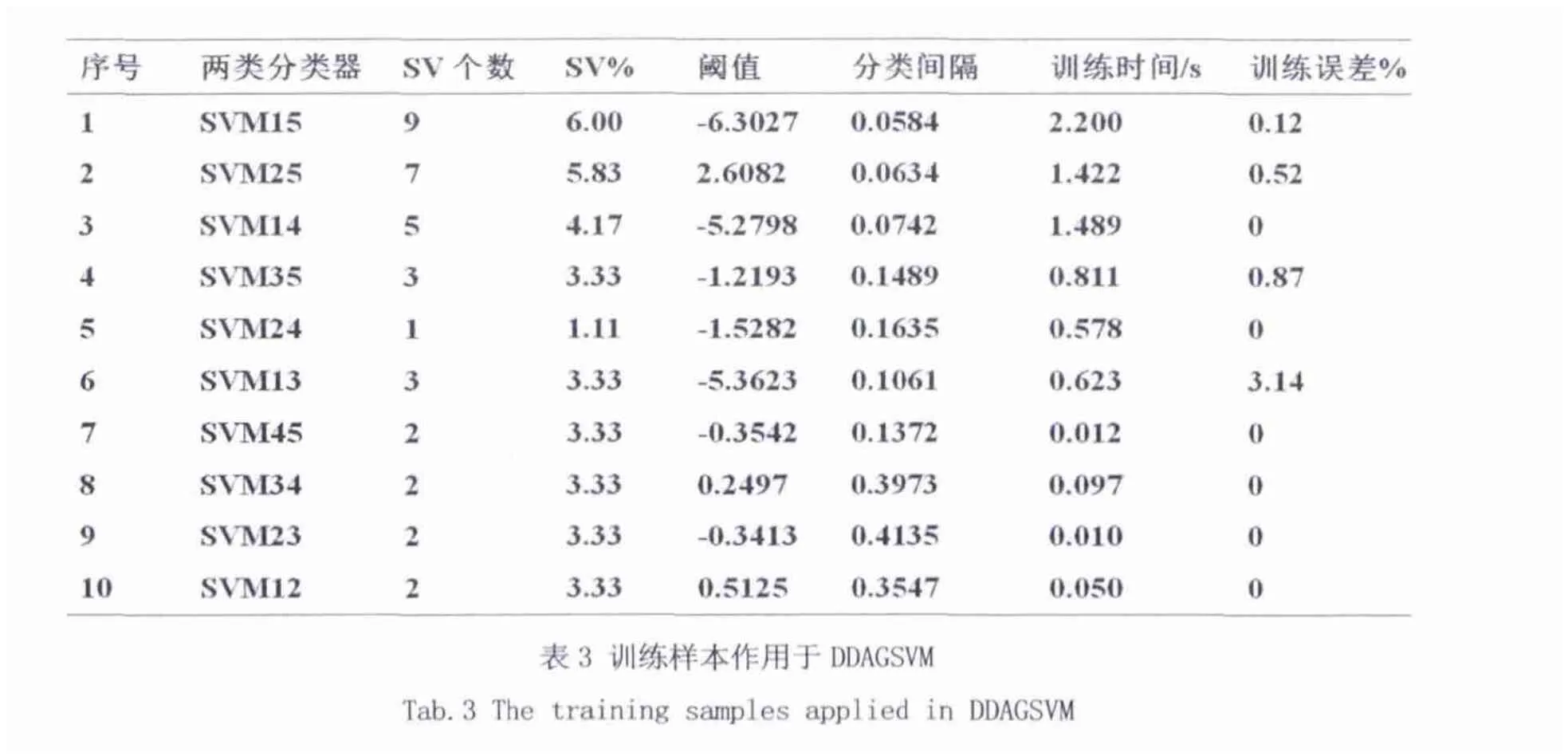
表5 SVM多分類器的分類情況Tab.5 The classified situation of multi-class SVM classification

5 總結

采用標準樣本Iris數據集進行研究，通過結構為4-10-3 BP神經網絡仿真，表明在少量樣本情況下SVM的分類精度均高于BP神經網絡，同時訓練時間明顯小于BP神經網絡，表現出更強的分類能力，適用于混合電路故障的模式識別。DDAG算法所需的訓練時間和測試精度均優于1-a-1算法和1-a-r算法，適合快速精確的模式識別。

針對高斯徑向基核函數，運用改進的網絡搜索方法進行了粗搜索和細搜索，得出的3D結果圖可以確定出SVM的最佳參數對。

基于SVM融合方法進行的混合電路故障診斷仿真結果表明，SVM適合少量樣本情況下的混合電路故障診斷。

[1] Liang F.An Effective Bayesian Neural Network Classifier with a Comparison Study to Support Vector Machine [J].Neural Computation，2003，15(8)：1959-1989.

[2] Chih-Chung Chang，Chih-Jen Lin.LIBSVM：a library of support vector machines[M].2001.

[3] YAN Wei-wu，SHAO Hui-be.Application of support vector machine nonlinear classifier to fault diagnosis[C]. Proceedings of the 4th World Congress on Intelligent Control and Automation.Shanghai，China：IEEE Press，2002，4：2697-2700.

[4] 崔長春，劉文林，鄭俊哲.支持向量機理論與應用[J].沈陽工程學院學報，2007，3(2)：170-172.

[5] HSU Chih Wei，LIN Chih Jen.A comparison of methods for multi-class support vector machines [J].IEEE Transactions on Neural Networks，2002，13(2)：415-425.

[6] 榮海娜，張葛祥，金緯東.系統辨識中支持向量機核函數及其參數的研究[J].系統仿真學報，2006，11：3204-3209.

[7] Wang Huai-long，Pan Qiang，Liu Hong.The Application of Improved SVM in Mixed Circuit[C].Proceedings of 2012 International Conference on Industrial Design and Mechanical Power.Huangshan，2012：493-496.