緊致優化DGHV全同態加密方案*

湯殿華，曹云飛，楊浩淼

0 引言

全同態加密是一種功能強大的加密技術，能夠在加密數據上執行任意的計算，同時將對應的計算映射到明文中，其計算結果仍為密文。可以說，全同態加密技術能夠全密態處理數據。采用該加密技術，可以將數據以加密形式外包給任何不可信服務器進行“密文計算”來獲取服務，保證了數據安全。全同態加密技術具有廣闊的應用前景，例如云安全、加密數據庫、密文檢索、網絡編碼［1］、搜索引擎的加密詢問等。

同態密碼技術對我們并不陌生，例如 RSA［2］、ElGamal［3］、Paillier［4］等加密方案。這些加密算法都具有同態性，但只有單個同態運算性質，不能同時具有“加同態”和“乘同態”，以致不能夠執行任意的密文計算。1978 年，Rivest，Adleman，Dertouzos［5］首次提出了這種“隱私同態”的概念，希望解決密文任意計算問題。直至2009年，Gentry基于理想格提出了第一個全同態加密方案［6］，實現了“隱私同態”的構想。

Gentry的方案基于理想格數學結構，運算復雜。Dijk等人避免了這種復雜的代數結構，提出一個整數上的全同態加密方案—DGHV方案［7］，其運算完全基于整數運算，更容易理解。全同態加密方案除了滿足能夠無限計算“同態加”和“同態乘”之外，還應滿足緊致性:密文尺寸需要保持有界，不能隨著同態操作而無限增大。在DGHV方案中，其類同態方案(Somewhat Homomorphic Scheme)的同態乘和同態加操作沒有進行類似于加密算法中的模運算，導致了密文尺寸的不斷增加。為了保證全同態加密方案的緊致性，DGHV方案的同態解密算法，在更新密文噪聲的同時，也將密文尺寸控制在?O(λ7)的水平，但在同態解密算法的內部運算過程中，密文數據的尺寸仍在不斷增加。

文中給出了一個緊致優化技術，使得DGHV方案中類同態方案和全同態方案均滿足緊致性要求，密文尺寸始終保持在?O(λ5)以內，而且保證了同態解密算法的內部運算的密文尺寸不增加。

1 準備知識

定義1 同態加密方案。同態加密方案由四個概率多項式時間算法組成 HE=(KeyGen，Enc，Dec，Evaluate):

KeyGen:根據安全參數λ，生成方案的公鑰pk、私鑰sk。

Enc:給出一個明文m，用公鑰pk加密明文m，得到密文c。

Dec:輸入私鑰和密文c，進行解密運算，輸出明文m'。

Evaluate:輸入公鑰 pk，t輸入線電路 Cir，一組密文 →c=(c1，c2，…，ct)，其中 ci=Encpk(mi)。輸出 c*=Evaluate(pk，Cir，→c)，且滿足 Dec(sk，c*)=Cir(m1，m2，…，mt)。

由定義1可以看出，同態加密方案除了包括傳統公鑰加密方案的所有算法(KeyGen，Enc，Dec)之外，還包括一個額外的運算算法Evaluate。該算法是用于同態處理一個電路，是方案同態性的體現，能夠在不解密條件下，對密文的操作實現了相應的明文操作，并且操作結果也為密態。

文中研究的方案是單比特的加密形式，即明文空間為{0，1}，所運算的電路為布爾電路，這樣就可以對應于計算機中的數字邏輯電路，而計算機所完成的所有程序都是通過數字邏輯電路執行，如果方案能夠同態運算所有的布爾電路，那么就可以密態完成計算機中所有程序及服務。

定義2 C-同態。設C是一個電路集合，HE是一個同態加密方案，任取一個電路Cir∈C，設其輸入線有t個。如果對任意的一組明文m1，m2，…，mt和所對應的一組密文 →c=(c1，c2，…，ct)(其中 ci=Encpk(mi))，有下面的等式成立:

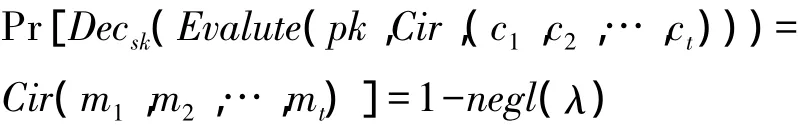
則稱該方案為C-同態，或者方案對于一個電路集合C是正確的，同時也稱C為方案HE的可許電路集合，當C是一個有限電路集合時，也稱方案為somewhat同態加密方案。

定義3 緊同態加密。如果存在一個多項式g=g(λ)，使得HE方案的Evaluate算法的輸出比特長度不超過g。則稱HE是一個緊同態加密方案。

注意:g與所運算的電路Cir、輸入密文數無關。表明隨著同態操作的進行，密文的尺寸始終保持在一個界之內，其尺寸獨立于同態操作數。

定義4 全同態加密方案。一個方案HE對所有的電路既是緊的，又是同態的，則稱其是一個全同態加密方案。

定理1自舉轉化定理。如果一個同態加密方案HE是能夠同態計算“自身解密電路”或“解密電路加上額外的門電路”，且滿足循環安全，那么該方案可以轉化為一個全同態加密方案。

2 DGHV全同態加密方案

本節描述Dijk等人所提出的DGHV方案［7］，其中包括用于構造全同態加密方案的基石—somewhat同態加密方案，和DGHV全同態加密方案。

2． 1 Somewhat同態加密方案

在DGHV方案中需要一些參數來控制各個變量的比特長度，其參數設置為:ρ=λ，ρ'=2λ，η=?O(λ2)，θ=?O(λ4)，γ=?O(λ5)，τ=γ+λ，其中 λ 為安全參數。

首先需要定義一個用于公鑰生成的分布，如下:

Somewhat同態加密方案 SHE=(KeyGen'，Enc'，Dec'，Evaluate')描述如下:

KeyGen'(λ):根據輸入的安全參數λ，隨機選擇 p←(2? +1)∩［2η-1，2η)。在分布 Dγ，ρ(p)中隨機選取 τ+1 個數(x0，x1，…，xτ)，以致 x0為其中最大的數，并x0mod p是偶數。若不滿足條件，重新選取直至滿足條件。令私鑰sk=p，公鑰pk=→x=(x0，x1，…，xτ)。

Enc'(pk，m):消息為 m∈{0，1}。隨機選擇一個整數 r∈(-2ρ'，2ρ')和一個 τ+1 維的比特向量 →v∈{0，1}τ+1。計算密文c=m+2r+2＜→x，→v＞mod x0。

Dec'(sk，c):輸出 m'=(c mod p)mod 2。

Evaluate'(pk，C，c1，c2，…，ct):根據輸入的公鑰pk，布爾算術電路 C，和 t個密文(c1，c2，…，ct)，執行整數上加法和乘法運算。輸出電路的結果c'。

該方案的同態操作可以分解為兩種基本操作:Add(c0，c1)=c0+c1，Mult(c0，c1)=c0×c1。

2． 2 全同態加密方案

為了將SHE方案轉化為全同態加密方案，Dijk等人采用“稀疏子集和”對方案的解密算法進行了壓縮，使得方案滿足自舉性，應用自舉轉化，從而獲得全同態加密方案。其方案FHE=(KeyGen，Enc，Dec，Evaluate)描述如下:

參數選取:κ=γη/ρ'，Θ=ω(κ log λ)，θ=λ。

KeyGen(λ):運行SHE方案的密鑰生成算法產生sk=p，pk=→x，設置K=?2κ/p?，隨機選取一個漢明重量 θ的比特向量 →s∈{0，1}Θ，設其指標集為 S={i|si=1}。均勻隨機選取 ui∈? ∩［0，2κ+1)，i=0，1，…，Θ-1，使其滿足 K=，令 yi=ui/2κ，i=0，1，…，Θ-1，令向量→y=(y0，y1，…，yΘ-1)。輸出私鑰SK=→s，公鑰PK=(→x，→y)。

Enc(PK，m):調用SHE方案生成c=Enc'(pk，m)。然后計算［c·yi］2，i=0，1，…，Θ-1，并對其二進制表達保留小數點后n=logθ+3位的精度，記為zi。得到新密文 ?c={c，(z0，z1，…，zΘ-1)}。

Evaluate(PK，C，c1，…，ct):將算術電路 C 中的運算替換成整數上加法和乘法運算，每個運算門的輸入線上加入解密電路，擴展成增強型解密電路。然后，將密文 c1，c2，…，ct輸入到電路中，首先進行重加密(同態解密)操作來更新密文，然后將更新后的密文c'輸入到電路門中進行運算，將門輸出作為主密文c″，并使用PK中的→y生成對應的其擴展密文 →z″，由此構成密文 ?c'=(c″，→z″)，如此在電路中運算下去。得到最后的輸出。

3 緊致優化技術

由第2節的方案描述可以看出，導致DGHV方案中somewhat同態加密方案密文尺寸增加的原因在于:Add(c0，c1)=c0+c1，Mult(c0，c1)=c0×c1沒有進行模操作。因此，文中的初始想法思想為:Add(c0，c1)=(c0+c1)mod x0，Mult(c0，c1)=(c0×c1)mod x0。

計算同態加法和同態乘法，需要進行模x0。但x0中帶有隨機噪聲項r0，模x0將引入一個新的誤差。需要對模操作之后的引入噪聲進行分析。

1)同態加法:由于兩個密文之和不會太大，其和的比特長度與輸入密文的尺寸大約一致，模x0只是帶入了一個小的x0倍數，可以確定引入的新誤差的上界。

2)同態乘法:兩個密文之積將變得非常大，其乘積的比特長度大約兩倍于輸入密文尺寸，模x0運算帶入了一個很大的x0倍數，同時帶入的新噪聲也非常大，無法確定其上界。所以我們對乘法進行優化，確保噪聲的可控性。

3． 1 同態操作緊致優化技術

優化過程需要一些輔助數據 x'0，x'1，…，x'γ，其都是非常靠近p的倍數，與方案的公鑰相似，但其參數的選取范圍不一樣，主要在于p的倍式因子q'i的選取。

對同態乘法作修改，c1，c2為兩個密文，兩個密文相乘之后，按順序進行分別模 x'γ，x'γ-1，…，x'0。即 opt(c1×c2)=(…(((c1×c2)mod x'γ)mod x'γ-1)…)mod x'0。

優化后的同態操作算法為:Add(c0，c1)=(c0+c1)mod x0，Mult(c0，c1)=opt(c1×c2)。

3． 2 噪聲分析

設m1，m2為兩個消息比特，由SHE加密算法分別產生其密文c1，c2。

模x0相當于加了一個x0的倍數，則存在兩個整數 k1，k2，使得

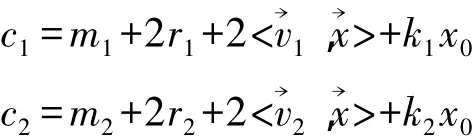
并記兩個密文中的噪聲為n1，n2。

1)同態加法的噪聲分析 SHE．Add(c1，c2):(c1+c2)mod x0

在方案中，|c1|＜x0/2，|c2|＜x0/2。由三角不等式得|c1+c2|＜x0。又由于|(c1+c2)mod x0|≤x0/2，根據這兩個不等式可得|(c1+c2)mod x0-(c1+c2)|≤(3/2)x0。設同態加法中引入的x0倍數因子為kAdd。

c1+c2mod x0=c1+c2+kAddx0，|kAddx0|=|(c1+c2)mod x0-(c1+c2)|≤x0，由此得|kAdd|≤1。

SHE．Add(c1，c2)所獲得新密文的噪聲為:

2)同態乘法的噪聲分析 SHE．Mult(c1，c2):opt(c1×c2)

首先分析模 x'γ所帶入的倍數因子 kMult，γ，即(c1×c2)mod x'γ=c1×c2+kMult，γx'γ。

加密算法產生的新密文c的比特長度為γ，c1×c2的比特長度最多為 2γ，由于 x'i∈［2γ+i-1，2γ+i)，則有|c1×c2|≤22γ＜2x'γ。結合|(c1×c2)mod x'γ|≤x'γ/2，利用三角不等式有|kMult，γx'γ|=|(c1×c2)mod x'γ-(c1+c2)|≤(5/2)x'γ，顯然 |kMult，γ|≤2。

按照優化算法的模順序，分析在模 x'γ-1過程中，所帶入的倍數因子 kMult，γ-1，即如下等式:

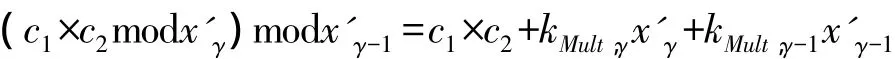
與模 x'γ噪聲分析思路類似，根據|(c1×c2)·mod x'γ|≤ x'γ/2 ＜ 22γ-1＜ 2x'γ-1和 |(c1× c2mod x'γ)mod x'γ-1|≤x'γ-1/2，可以得到|kMult，γ-1|≤2。

同理分析可得|kMult，i|≤2，i=0，1，…，γ-1。

SHE．Mult(c1，c2)所獲得新密文的噪聲:nMult=那 么 |nMult|＜ |n1|· |n2|+(γ+1)·2ρ+1

綜上所述，同態加法運算帶入的新噪聲為2ρ，在同態乘法運算帶入的新噪聲為(γ+1)·2ρ+1。新的噪聲加入，會降低方案的運算能力，下面將對其詳細分析，并給出方案的支持同態運算的多項式次數。

3． 3 優化方案的同態運算能力

根據Dijk等人的分析思路，將所需運算的電路C 表示成 t個變元的多項式 f(x1，x2，…，xt)，設其多項式次數為d。這里把SHE能夠同態運算多項式次數d作為方案的同態能力指標估計。由文獻［7］引理A．1可知，Enc'(pk，m)所產生的新鮮密文的噪聲為τ·2ρ+3，并記為X;同態加法中引入的新噪聲記為 A=2ρ;同態乘法引入的新噪聲記為 B=(γ+1)·2ρ+1。

首先分析一個d次單項式xi1xi2xi3…xid的噪聲，由于乘法中噪聲變化為|nMult|＜|n1|·|n2|+B。則d次單項式的噪聲為:(…(((X·X+B)·X+B)·X+B)…)X+B，歸納得Xd+BXd-2+BXd-3+…+BX+B=Xd+B·(Xd-1-1)/(X-1)。對多項式 f(x1，x2，…，xt)進行放縮處理，將其每一項都放大為一個d次單項式，由于 f(x1，x2，…，xt)一共有‖f‖1項，則將進行‖f‖1-1個同態加法，引入新噪聲為(‖f‖1-1)A。綜合分析可以得出經過 f(x1，x2，…，xt)同態運算之后的噪聲為:‖f‖1(Xd+B·(Xd-1-1)/(X-1))+(‖f‖1-1)A，為了保證解密的正確，噪聲上界不能超過p/8。那么可以得到以下等式:

代入 X= τ·2ρ+3，A=2ρ，B=(γ+1)·2ρ+1。B/(X-1)≈(γ+1)/4τ，B/X(X-1)≈(γ+1)/τ2·2ρ+5，忽略此這兩項。粗略得到方案的支持同態運算的多項式次數，即同態運算能力為:

4 結語

緊致性是全同態加密方案的必要條件。DGHV方案通過同態解密算法取得整個全同態加密方案的緊致性，導致每個電路輸出的密文尺寸為?O(λ7)。文中在同態操作中引入模運算，并對同態乘法進行優化，使得DGHV方案在同態操作取得緊致性，將密文尺寸控制在?O(λ5)，但由于需要在同態操作時進行γ個模運算，因此該優化技術增加了同態操作的計算量。再則，文中的緊致性技術使得同態解密算法［8］內部運算中的密文尺寸不增長，這可以使得全同態加密方案中κ的選取由=γη/ρ'變成γ+2，參數設置變得更小。

［1］ 張盛勇，陳世康．網絡編碼的安全問題初探［J］．通信技術，2012，45(01):105-107．

ZHANG Sheng-yong，CHEN Shi-kang．Explortion on Security of Network Coding［J］．Communications Technology，2012(01):105-107．

［2］ RIVEST L R，SHAMIR A，ADLEMAN L．A Method for Obtaining Digital Signatures Public Key Cryptosystem［J］．Communication of ACM，1978，21(01):120-126．

［3］ ELGAMAL T．A Public-Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms［J］．Information Theory ，IEEE Transactions，1985，31(04):469-472．

［4］ PAILLIER P．Public-key Cryptosystems based on Composite Degree Residuosity Classes［C］//In J．Stern(Ed．)，EUROCRYPT'99．［s．l．］:Springer，1999:223-238．

［5］ RIVEST L R，ADLEMAN L，DERTOUZOSL M．On Data Banks and Privacy Homomorphisms［C］//In Foundations of Secure Computation．［s．l．］:Academic Press，1978:169-180．

［6］ GENTRY C．Fully Homomorphic Encryption Using Ideal Lattices［C］//In STOC'09．［s．l．］:ACM，2009:169-178．

［7］ DIJK VAN M，GENTRY C，HALEVIS，et al．Fully Homomorphic Encryption over the Integers［C］//In Proc．of Eurocrypt．［s．l．］:Springer，2010:24-43．

［8］ 湯殿華，祝世雄，曹云飛．整數上全同態加密方案的重加密技術［J］．信息安全與通信保密，2012(01):76-79．

TANG Dian-hua，ZHU Shi-xiong，CAO Yun-fei，Recrypt Technology of A Fully Homomorphic Encryption over Scheme Integers［J］．Information Security and Communictions Privacy，2012(01):76-79．