條件非線性最優擾動在可預報性問題研究中的應用

穆穆 段晚鎖

1中國科學院大氣物理研究所大氣科學和地球流體力學數值模擬國家重點實驗室，北京100029

2中國科學院海洋研究所，青島266071

1 引言

可預報性是數值天氣預報和氣候預測研究的基本問題之一。在可預報性問題研究中，關于預報結果不確定性的估計是可預報性研究的重要問題之一。Tennekes（1991）指出，對于一個預報產品，如果沒有估計其可能的預報誤差，那么這個預報產品是不能夠被使用的。事實上，早在 1957年，Thompson（1957）已經意識到了估計預報結果不確定性的重要性，業務天氣預報也從此開始嘗試在每一次預報中定量估計初始場不確定性的發展。這種觀點后來也被海氣耦合系統的預報所采納（Moore and Kleeman, 1996; Samelson and Tziperman, 2002;Mu et al., 2007a; Duan et al., 2009; Yu et al., 2012a,2012b）。通過對預報誤差演變規律的研究以及對預報誤差的估計，人們對熱帶海氣耦合系統的可預報性，獲得了更為清晰的認識和理解。

可預報性研究的另一個關鍵問題是探尋所關注的天氣和氣候事件發生的前期征兆，即何種初始異常會發展成所關注的天氣或氣候事件（Moore and Kleeman, 1996; Duan et al., 2004; Duan et al., 2012）。這也是動力氣象學與氣候動力學中的中心問題之一。在一定條件下，最容易發展成某一天氣或氣候事件的初始異常，我們稱其為該事件的最優前期征兆（Duan et al., 2004）。如何通過觀測（或同化）捕捉到初始場（分析場）中的這種前期征兆信號是天氣和氣候預報中的關鍵問題。國際上有研究使用線性奇異向量（LSV）方法研究天氣和氣候事件的最優前兆信號。如，Moore and Kleeman（1996）將LSV初始距平描述的海溫狀態作為El Ni?o事件發生的前期征兆。

LSV是線性模式中增長最快的一類初始擾動，該方法最早由 Lorenz（1965）將其引入氣象學研究。它不僅被用于可預報性最優前期征兆問題的研究，同時也被廣泛地用于研究預報誤差增長的可預報性問題。LSV基于線性理論，其使用的前提條件是初始擾動充分小，其發展能夠近似地由切線性模式（TLM）來描述。然而，大氣和海洋的運動是非線性的，天氣和氣候的可預報性不可避免地會受到非線性物理過程的影響。所以，基于線性模式的LSV不能充分反映非線性物理過程的影響，不能用于描述非線性模式中增長最快的有限振幅的初始擾動（Mu et al., 2003）。在可預報性研究中，LSV不能有效代表天氣和氣候事件的最優前期征兆和增長最快初始誤差（Duan et al., 2004; Mu et al.,2007a, 2007b）。

為了考察非線性的影響, Mu et al.(2003) 提出了條件非線性最優擾動（CNOP）方法。CNOP代表了具有一定物理約束條件且在預報時刻具有最大非線性發展的一類初始擾動；LSV代表了切線性模式中具有最大增長率的一類初始擾動，CNOP是LSV在非線性系統中的自然推廣。CNOP在預報時刻的增長率可能沒有LSV大，但其在預報時刻的非線性發展是最大的，從而代表了在預報時刻對預報結果有最大影響的一類初始誤差，也代表了最容易發展成一類天氣或氣候事件的前期征兆。因此，在可預報性研究中，CNOP比LSV具有更重要的作用。尤其在非線性系統中，CNOP可以刻畫有限振幅擾動大小的發展，LSV只能描述充分小初始擾動的演變，而這正是非線性影響的結果。所以，通過比較CNOP和LSV，可以揭示非線性物理過程對可預報性的影響。

CNOP方法首先被應用于ENSO可預報性的研究，用來尋找ENSO事件的最優前期征兆和探討預報結果不確定性問題（尤其是春季可預報性障礙(SPB) 問題）（Duan et al., 2004; Mu et al., 2007a,2007b; Duan et al., 2009; Duan et al., 2012; Yu et al.,2009; Yu et al., 2012a, 2012b）。繼而又將CNOP方法應用于熱鹽環流（THC）穩定性和敏感性問題的研究中，探討非線性過程對 THC穩定性和敏感性的影響（Mu et al., 2004; Wu and Mu, 2009）。所有這些工作表明，在考慮有限振幅初始擾動或/和較長預報時間的情況下，CNOP和LSV存在明顯區別。對于非線性大氣和海洋系統，我們相信CNOP的結果更能刻畫大氣和海洋的非線性運動特征，因此在估計天氣和氣候的預報結果不確定性的研究中，我們應該使用CNOP方法。Riviere et al.（2008）也將CNOP方法用于一個二層準地轉模式研究非線性物理過程對斜壓不穩定流的影響。Terwisscha van Scheltinga （2007）通過一種隱式4D-Var方法計算了描述Double Gyre海洋環流模式的CNOP，研究了有限振幅double gyre環流的穩定性，揭示了非線性物理過程的影響。CNOP方法還被應用于集合預報和目標觀測敏感區的研究，取得了滿意的結果。這些研究拓展了CNOP方法的應用，揭示了CNOP更豐富的物理意義，為改進天氣預報和氣候預測的預報技巧提供了新思路（Duan and Mu, 2009）。

近年來，CNOP方法得到了進一步發展，而且在對我國天氣和氣候異常有重要影響的 ENSO事件、黑潮路徑變異、臺風和阻塞事件的可預報性研究中的應用取得了重要進展。Mu et al.（2010）考慮到實際天氣預報和氣候預測初始誤差和模式誤差同時存在的情形，將CNOP方法拓展到既考慮初始擾動又考慮數值模式參數擾動。拓展的CNOP方法要求求解初始擾動和模式參數擾動的組合模態的最優模態，尋找導致最大預報誤差的初始誤差和模式參數誤差的組合模態。應用拓展的CNOP方法，Yu et al.（2009）和 Yu et al.（2012a）考察了影響ENSO事件SPB的誤差因子，強調了初始誤差是導致SPB的主要誤差來源，并且Yu et al.（2012b）和Duan and Wei（2012）先后在中等復雜程度模式和完全耦合的GCM模式的回報試驗中發現了類似的初始誤差模態，從而闡明在實際預報中，如果通過資料同化或目標觀測方法濾掉CNOP類型的初始誤差，ENSO預報技巧可能會被大大提高；拓展的CNOP方法也被Wang et al.（2012）用于黑潮路徑變異的可預報性研究，揭示了初始誤差是導致黑潮路徑變異預報不確定性的主要誤差因子，其伴隨的局地性特征為黑潮路徑變異預報的目標觀測敏感區提供了有用的信息。另外，CNOP方法也被應用于阻塞的可預報性，探討了阻塞事件最優前期征兆（OPR）和最快增長初始誤差（OGR）的相似性及其伴隨的局地性特征，從而為確定阻塞預報目標觀測敏感區提供了新方法，為提高數值天氣預報和氣候預測的預報技巧開拓了新思路（Jiang and Wang,2010; Mu and Jiang, 2011）。用CNOP確定目標觀測敏感區的思路被較成功地應用于臺風的目標觀測研究，為確定臺風預報的初值敏感區、進而提高臺風預報技巧提供了重要指導意義（Wang and Tan,2009; Qin and Mu, 2011a, 2011b; Zhou and Mu, 2011;Chen and Mu, 2012; Zhou and Mu, 2012a, 2012b）。可見，CNOP方法在原有應用研究的基礎上，學者們近年來進一步將其用于實際天氣預報或氣候預測直接面對的一些困難問題（如目標觀測敏感區）的研究，獲得了有特色的成果，為提高數值天氣預報和氣候預測的預報技巧提供了新思路。

該文將簡要回顧上述CNOP方法的拓展及其應用的研究進展。第二節將介紹拓展的CNOP方法及其物理意義；第三節敘述CNOP方法在ENSO可預報性問題研究中的應用；第四節回顧CNOP在黑潮路徑變異可預報性研究中的應用；第五節闡述阻塞前期征兆和最快增長初始誤差的相似性及其對目標觀測的指示意義；第六節將說明CNOP在臺風目標觀測中的應用。最后，在第七節討論上述成果對于改進天氣預報和氣候預測的預報技巧的科學指導意義和應用前景。

2 條件非線性最優擾動方法的拓展

Mu et al.(2003) 提出的CNOP是指給定物理約束條件的具有最大非線性發展的一類初始擾動，它既可以用來研究最容易導致某一天氣或氣候事件的初始異常，又可以研究對預報結果具有最大影響的一類初始誤差，這兩個問題是天氣和氣候可預報性研究中的兩個關鍵問題。因此，CNOP在有關初始場的可預報性問題研究中具有重要作用。考慮到實際天氣預報和氣候預測初始誤差和模式誤差同時存在的情形，Mu et al.（2010）進一步將上述CNOP方法拓展到初始誤差和數值模式參數誤差同時存在的情形，并提出了條件非線性最優參數擾動（CNOP-P）的概念。拓展的CNOP（為方便敘述，以下我們也稱之為 CNOP），即是求解初始擾動和模式參數擾動的最優組合模態。CNOP有兩種特殊情形：一種是Mu et al.（2003）提出的僅與初始擾動有關，并且在預報時刻具有最大非線性發展的CNOP初始擾動，以下將之記為 CNOP-I；另一種情形則只與數值模式參數擾動有關，即CNOP-P，CNOP-P導致在預報時刻，預報結果與參考態有最大差別。CNOP方法既可以用來研究由初始誤差引起的第一類可預報性問題，又可以研究由參數誤差引起的第二類可預報性問題，同時也可用于研究初始誤差和參數誤差同時存在的情形。本節將簡要回顧CNOP方法及其物理意義。

2.1 CNOP的定義

假定狀態向量w的發展由以下動力系統方程描述:

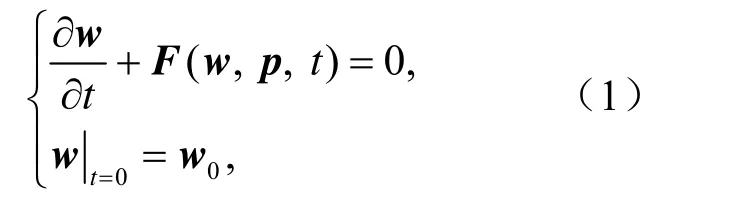
其中，w( x,t) = (w1( x,t), w2(x,t) , …,wl( x,t))為包含l個狀態變量（如，海表溫度、溫躍層深度、風速等）的狀態向量；w0是初始條件；x =(x1, x2,… ,xn),x ∈ Ω（Ω是歐氏空間Rn的一個集合）；t是時間，0≤t＜∞；p =( p1, p2, … , pm)是模式參數向量；F是非線性算子。

若動力系統方程（1）和初始條件已知，則未來時刻狀態可以通過對方程（1）積分確定，

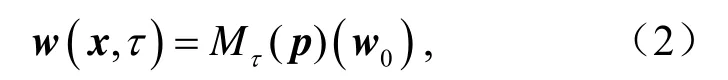
這里Mτ(p)代表含有參數p的動力系統方程（1）從0時刻到τ時刻的傳播算子。如果方程（2）對應于初始條件U0和U0+u0的解為U(t)和U(t)+u(t)，那么其在τ時刻的解為：

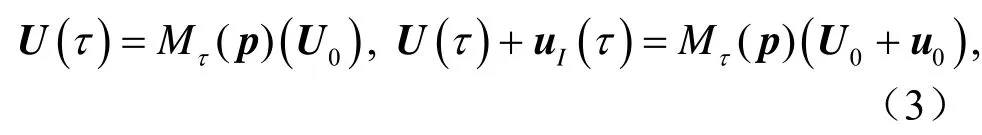
其中，u0是U(t) 的初始擾動，uI(τ)則代表了初始擾動的非線性發展。

如果p'是在模式參數向量P上的參數向量擾動,方程（2）對應于P和P+ p'的兩個解可以表示為

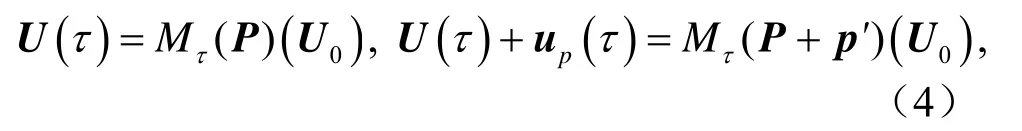
這里up(τ) 代表了由于參數擾動p'導致的預報結果和參考狀態U(τ) 的偏差。

當同時考慮初始條件和模式參數的擾動時, 方程（2）的兩個解為

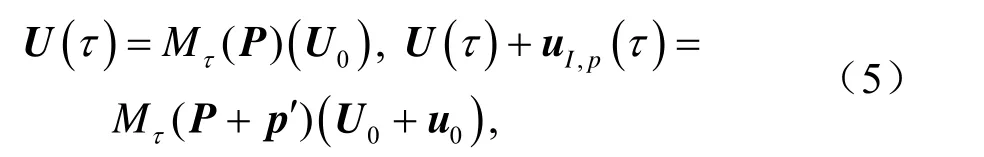
這里uI,p(τ) 代表了由初始擾動和模式參數擾動共同導致的預報結果和參考態U (τ)的偏差。

定義如下非線性優化問題:

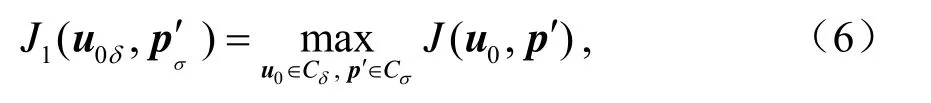
其中，J (u0, p ') = Mτ(P + p')( U0+ u0)- Mτ(P) (U0),u0和p' 分別是疊加在參考態初值U0和模式參數向量P上的擾動，u0∈ Cδ, p′ ∈Cσ是各自的約束條件。通過解優化問題（6），即可得到最優初始擾動和參數擾動的聯合模態(u0δ; pσ′)。在給定約束條件下，該模態導致預報時刻τ的預報結果和參考態Mτ(P) (U0)的偏差最大。Mu et al.（2010）將該模態定義為 CNOP。CNOP包含兩種特殊情形：一種特殊情形是 CNOP-I (即優化問題（7）式中的u0δ,I),即Mu et al.（2003）提出的CNOP初始擾動，其在預報時刻具有最大的非線性發展。CNOP-I可通過求解下面優化問題得到:

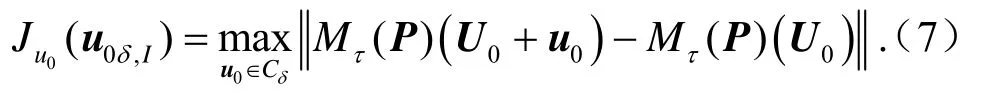
CNOP的另一種特殊情形是CNOP-P (即（8）式中的p′σ,p)。CNOP-P代表了導致預報時刻預報結果與參考態的偏差最大的一類參數擾動，可通過解下述優化問題得到：

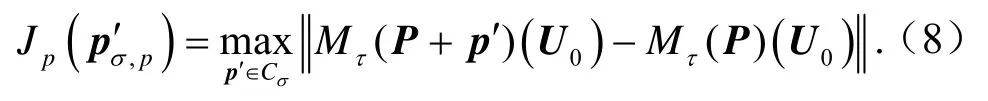
2.2 CNOP的物理意義

CNOP代表了滿足一定物理約束條件的初始擾動和模式參數擾動的最優組合模態，該模態導致預報結果與參考態的偏差最大。在可預報性研究中，CNOP代表了導致最大預報誤差的一類初始誤差和參數誤差的組合模態。

CNOP-I是CNOP的一種特殊情形。作為初始擾動，CNOP-I不僅可以描述最容易發展成某一天氣或氣候事件的最優前期征兆，而且當CNOP-I被考慮為疊加在某一天氣或氣候事件上的初始誤差時，它可以描述在預報時刻對預報結果影響最大的一類初始誤差；CNOP-I也可用于表征非線性最不穩定（或最敏感）的初始擾動模態，該類擾動在預報時刻具有最大的非線性發展。

CNOP-P是CNOP的另一種特殊情形。CNOP-P可以代表在預報時刻對預報結果具有最大影響的一類參數誤差；在敏感性研究中，它也可以用來描述最敏感的參數擾動，從而為參數的敏感性排序提供有用的信息；通過CNOP-P描述的敏感參數，我們也可以據此確定最需要通過觀測定量確定的參數。

如上所述，CNOP可以代表導致最大預報誤差的初始誤差和參數誤差的組合模態，CNOP-I誤差和CNOP-P誤差分別代表導致最大預報誤差的初始誤差和參數誤差。因此，通過CNOP誤差，我們不僅可以探討初始誤差和參數誤差對預報結果不確定性的影響，而且可以分辨初始誤差和參數誤差的預報結果不確定性產生中的相對重要性，最終確定導致預報結果不確定性的主要誤差因子。

2.3 CNOP的計算

已有的優化算法主要是用于求解極小值問題，但 CNOP優化問題（6）是一個極大值問題，所以當計算CNOP時，需要將極大值問題轉變為極小值問題。即將目標函數（7）改寫為：

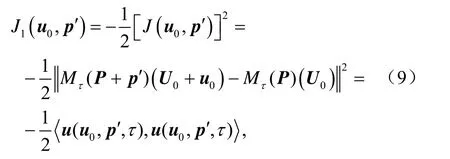
其中＜·＞表示內積，這樣極大值問題（6）就轉換為極小值問題，從而可用已有的優化算法求解（9）的極小值，得到 CNOPs。求解 CNOPs，一個重要的步驟是計算目標函數關于初始擾動和參數擾動的梯度。Mu et al.（2010）給出了利用伴隨模式計算目標函數J1的梯度公式，為進一步使用數值模式計算目標函數梯度提供了理論指導。Mu et al.（2010）給出的計算梯度公式為

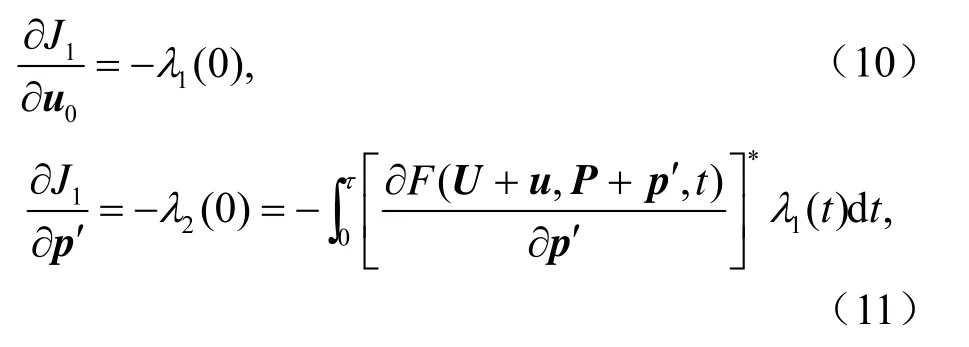
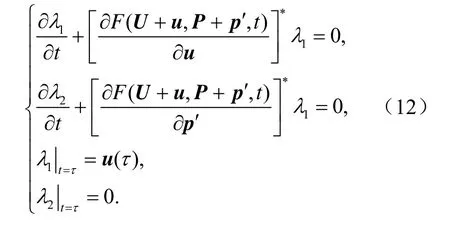
其中[]?·表示伴隨算子，1()tλ和2()tλ滿足，利用上述梯度信息，我們可以使用優化算法，如SPG2 (Spectral Projected Gradient 2) (Birgin et al.,2000)，SQP (Sequential Quadratic Programming)Powell et al., 1982) 和LBFGS-B (Limited memory Broyden-Fletcher-Goldfarb-Shanno for Boundconstrained optimization) (Liu and Nocedal, 1989;Zhu et al., 1997) 等計算CNOPs。

上述已經表明，CNOP的求解需要采用伴隨技術，然而伴隨模式的編寫非常繁雜，需要花費大量時間，限制了該方法的推廣應用。為了克服這一困難，Wang and Tan（2009）提出了基于集合投影技術的CNOP求解算法，避免了伴隨編寫困難。該算法使用多個相互線性獨立或者說正交的初始擾動（x′）得到相應的預報增量（y′），通過集合方法建立x′和y′之間的統計相關模型，用該統計模型向后積分計算目標函數的梯度，以此進行非線性最優化迭代，從而得到滿足初始約束條件且在預報時刻有最大非線性發展的CNOPs。Wang and Tan（2009）表明，新算法能夠很好地抓住CNOP發展的非線性特征，而且基于集合投影的新算法和基于伴隨算法產生的CNOPs空間結構幾乎完全相同。也就是說，基于集合投影計算CNOP的新算法是有效可行的。

新算法的提出在一定程度上推廣了CNOP在不同模式中的應用。例如，Wang and Tan（2009）將新算法應用于 GRAPES模式等研究臺風的目標觀測問題，從而肯定了CNOP新算法的有效性。

3 CNOP在El Ni?o事件春季可預報性障礙（SPB）問題研究中的應用

ENSO事件的“春季可預報性障礙”（SPB）問題是ENSO可預報性研究的一個重要內容。SPB現象是指ENSO預報具有較大預報誤差，且預報誤差的最快發展發生在春季和夏初，即預報誤差的發展呈現顯著的季節依賴性特征。國際上許多研究探討了ENSO事件的SPB問題，但SPB產生的機制至今仍撲朔迷離，具有很大爭議。而且，在業務預報中，ENSO事件的 SPB問題仍然嚴重影響著ENSO的預報技巧，采用何種有效的預報策略減弱或消除SPB至今尚不清楚。作者們近期的工作強調了初始誤差的特定結構及其局地性特征在 El Ni?o事件SPB現象中的重要作用，進而提出了用目標觀測的方法提高ENSO預報技巧的新思路。

CNOP誤差導致最大預報誤差，所以最有可能導致 El Ni?o事件的 SPB現象 (Mu et al., 2007a,2007b)。因此，Duan and Zhang（2010）用一個理論ENSO模式（WF96模式；Wang and Fang, 1996）研究了CNOP誤差（即初始誤差和模式參數誤差的最優聯合模態）對SPB的影響。結果表明，CNOP誤差導致El Ni?o事件產生最大的預報誤差，尤其在春季誤差增長最快，具有明顯的季節依賴性特征。CNOP誤差導致了El Ni?o事件顯著的SPB現象。進一步研究表明，CNOP-P誤差導致較小的預報誤差，預報誤差在每個季節的增長率也很小，而且沒有明顯的季節依賴性，沒有導致El Ni?o事件的SPB現象。這些結果說明，初始誤差可能是導致El Ni?o事件SPB現象的主要誤差因子。Yu et al.（2012）進一步利用中等復雜程度的Zebiak-Cane模式，研究了初始誤差和模式參數誤差對El Ni?o事件SPB現象的影響，考察了它們在SPB產生中的相對重要性。結果表明，CNOP-P誤差導致的預報誤差既沒有顯著的季節依賴性發展，對預報結果不確定性也沒有大的貢獻，因而未能導致El Ni?o事件的SPB現象。然而對于初始誤差，CNOP-I誤差不僅導致顯著的預報結果不確定性，而且呈現明顯的季節依賴性發展，發生了顯著的 SPB現象。CNOP-I誤差和CNOP-P誤差的組合模態也導致了明顯的 SPB現象，而且組合模態導致的預報誤差與CNOP-I誤差導致的預報誤差相差不大。所以，CNOP-I誤差可能更容易導致 SPB現象。綜上，Duan and Zhang(2010) 和Yu et al.(2012) 一致表明，初始誤差可能比參數誤差更容易導致El Ni?o事件的SPB現象，即初始誤差在El Ni?o事件SPB現象的產生中具有更加重要的作用，可能是SPB誤差增長的主要誤差來源。

Mu et al.（2007b）研究發現CNOP-I誤差容易導致El Ni?o事件顯著的SPB現象，而且他們也發現存在一些其他類型初始誤差，該類誤差與CNOP-I誤差大小相同，只是空間結構不同，然而它們卻沒有導致大的預報誤差，也沒有明顯的季節依賴性發展，最終未能導致SPB。該結果說明SPB的發生依賴于初始誤差的特定空間結構，即具有特定空間結構的初始誤差可能更容易導致El Ni?o事件的SPB現象。為進一步研究該問題，Yu et al.（2009）針對不同強度的El Ni?o事件，考察了CNOP-I誤差、LSV誤差和隨機初始誤差在上述El Ni?o事件SPB產生中的作用（圖1和2）。結果仍然表明，CNOP-I誤差導致El Ni?o事件顯著的SPB現象，但LSV誤差導致的SPB現象較CNOP-I誤差弱，隨機初始誤差導致的預報誤差則在每個季節的增長率可以忽略不計，而且其最大季節增長率沒有明顯的季節依賴性，未能導致SPB現象。所以，Yu et al.（2009）進一步表明，El Ni?o事件SPB的發生依賴于初始誤差的空間結構，具有CNOP-I誤差空間結構的初始誤差更容易導致SPB。CNOP-I誤差可以分為兩類（Yu et al., 2009）：一類誤差的 SSTA分量在赤道東太平洋呈現正異常，而在赤道中西太平洋呈現負異常，溫躍層深度則沿著赤道一致加深；另一類誤差則呈現與前者幾乎相反的模態。由此可見，CNOP-I誤差盡管存在不同的空間結構，但空間模態一致地具有局地性特征，即誤差能量集中于某一特定局地區域。

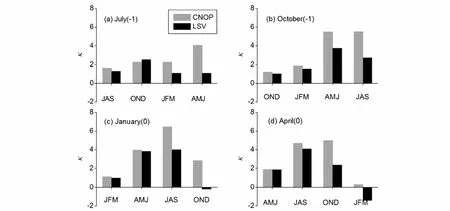
圖1 Zebiak-Cane模式中8次具有代表性的El Ni?o事件（初始變暖的時間分別為1月、4月、7月和10月的相對強和弱的El Ni?o事件）的CNOP-I誤差和LSV誤差導致的SSTA（SST anomaly）預報誤差（單位：°C）的季節增長率κ.預報的起始月為 (a) July (―1), (b) October (―1), (c) January (0)和 (d) April (0) (0和―1表示El Ni?o年和前一年).LSV誤差的季節增長率幾乎在每個季節都小于CNOP-I誤差的增長率.這里的預報誤差季節增長率用一個季節內預報誤差的增長與該季節時間跨度的比值來度量Fig.1 Ensemble mean of the seasonal growth rate κ of the SSTA prediction errors (unit: °C) caused by the CNOP-I-type errors and the LSV-type errors for eight El Ni?o events in the Zebiak-Cane model, where the seasonal growth rate of the prediction errors is measured by the ratio of the growth of the prediction errors in one season to the time length of the season.The start months of the predictions are (a) July (―1), (b) October (―1), (c) January (0), and (d) April (0).The growth rates of the LSV-type errors in almost each season are smaller than those of the CNOP-type errors

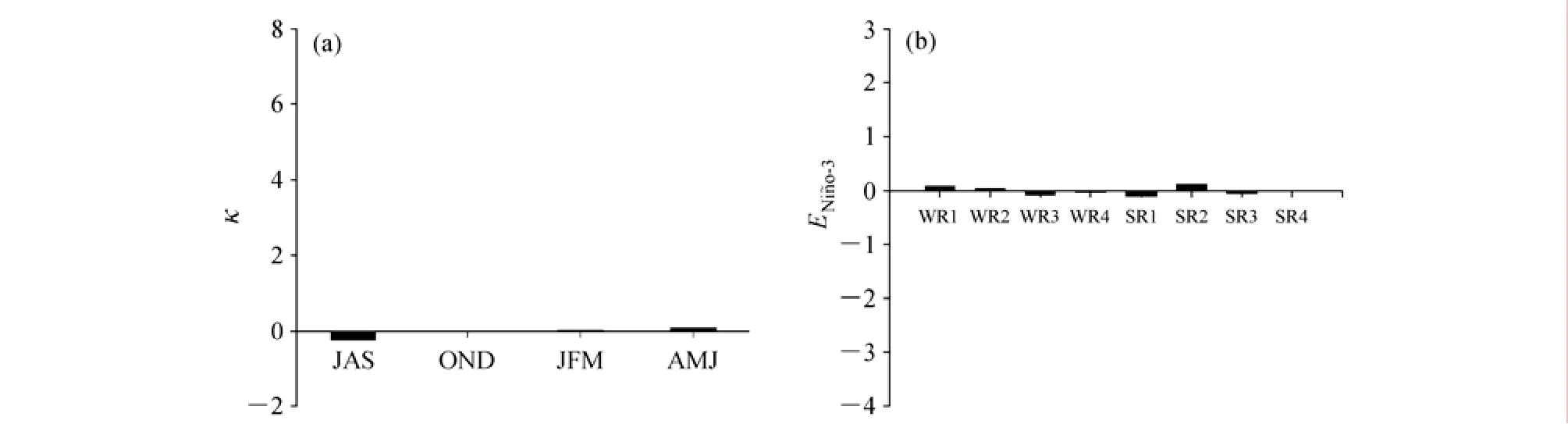
圖2 Zebiak-Cane模式中8次El Ni?o事件的（a）隨機初始誤差的季節增長率及其（b）導致的SSTA預報誤差（單位：°C）的集合平均，橫坐標的數字表示8次El Nino事件。引自Yu et al.(2009)Fig.2(a) The ensemble mean of the seasonal growth rate κ of the random initial errors for eight El Ni?o events in the Zebiak-Cane model; (b) the SSTA prediction errors (unit: °C) of the eight El Ni?o events that are caused by the random initial errors (the numbers on the horizontal axis denote eight El Nino events).From Yu et al.(2009)

上述兩類 CNOP-I誤差是通過考察模式中 El Ni?o事件而得到的對預報結果具有最大影響的初始誤差。那么，這些誤差是否存在于ENSO的實際回報試驗中？我們試想，如果在ENSO預測的初始分析場中確實存在與 CNOP-I類似的誤差（記為CNOP-I-like誤差），那么我們可以通過合適的方法濾掉CNOP-I誤差，進而提高ENSO預報技巧。因此，首先要弄清楚的一個關鍵問題是：在 ENSO的預測試驗中是否存在CNOP-I誤差？Yu et al.（2012b）表明，在所考察的 Zebiak-Cane模式的最新版本(LDEO5) (Chen et al., 2004) 關于1980年1月至1999年12月的回報試驗的240個初始分析場誤差中，與CNOP-I-like誤差模態相似性較高的誤差，一般對應于較大的預報誤差，也就是說，在LDEO5關于El Ni?o的回報試驗中，確實存在CNOP-like-I誤差，而且該類誤差對應了較大的預報誤差。 Duan and Wei（2012）探討了復雜GCM模式—FGOLAS-g模式關于El Ni?o回報試驗的初始分析場誤差。結果表明，在FGOALS-g關于1982～2007年ENSO事件的回報試驗中，導致El Ni?o事件顯著SPB現象的初始分析誤差的主模態具有CNOP-I-like誤差的空間結構。該結果在一定程度上說明，在FGOALS-g回報試驗中，與CNOP-I-like相似的誤差更容易導致El Ni?o預報結果具有較大不確定性。從Zebiak-Cane模式和FGOALS-g模式的回報試驗看，CNOP-I-like誤差可能確實存在于ENSO預測中。因此，我們應該研究如何根據CNOP-I誤差的特點想辦法濾掉ENSO預測中的CNOP-I-like誤差,進而提高ENSO的預報技巧。

綜上，初始誤差是El Ni?o事件SPB現象的主要誤差來源，而具有CNOP-I誤差模態的初始誤差更容易導致 SPB，該類誤差不僅是所考察模式 El Ni?o事件的最優增長初始誤差，而且存在于有關模式的實際回報試驗中，因此，如果在預報中通過合適的方法濾掉CNOP-I-like誤差，ENSO的預報技巧可能會大大提高；另一方面，CNOP-I誤差的空間分布具有明顯的局地性特征，即誤差主要集中在某一特定區域。Yu et al.（2012b）表明，在CNOP-I誤差集中的局地性區域減小誤差，ENSO預報誤差會大大減小，CNOP-I誤差集中的區域可能代表了ENSO預測的敏感區。該結果建議我們可以通過在CNOP-I敏感區進行目標觀測，消除CNOP-I-like誤差，改進初始場，進而提高ENSO預報技巧。

4 CNOP在黑潮路徑變異可預報性研究中的應用

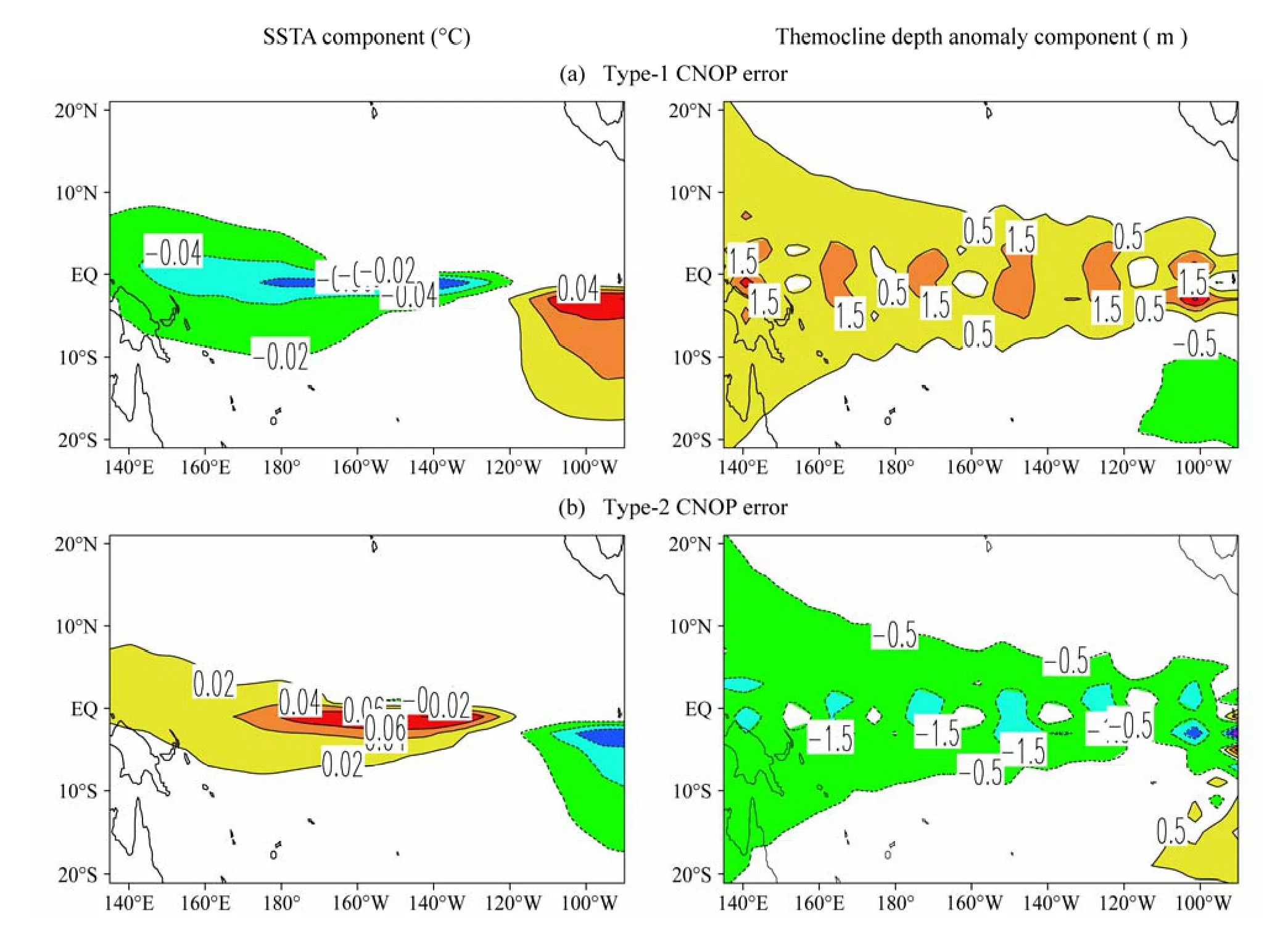
圖3 兩類CNOP-I誤差。左列為SSTA分量，右列為溫躍層深度異常分量。引自Yu et al.(2009)Fig.3 The patterns for the two categories of CNOP-I-type errors.The left column is for the SSTA component, while the right column is for the thermocline depth anomaly.From Yu et al.(2009)

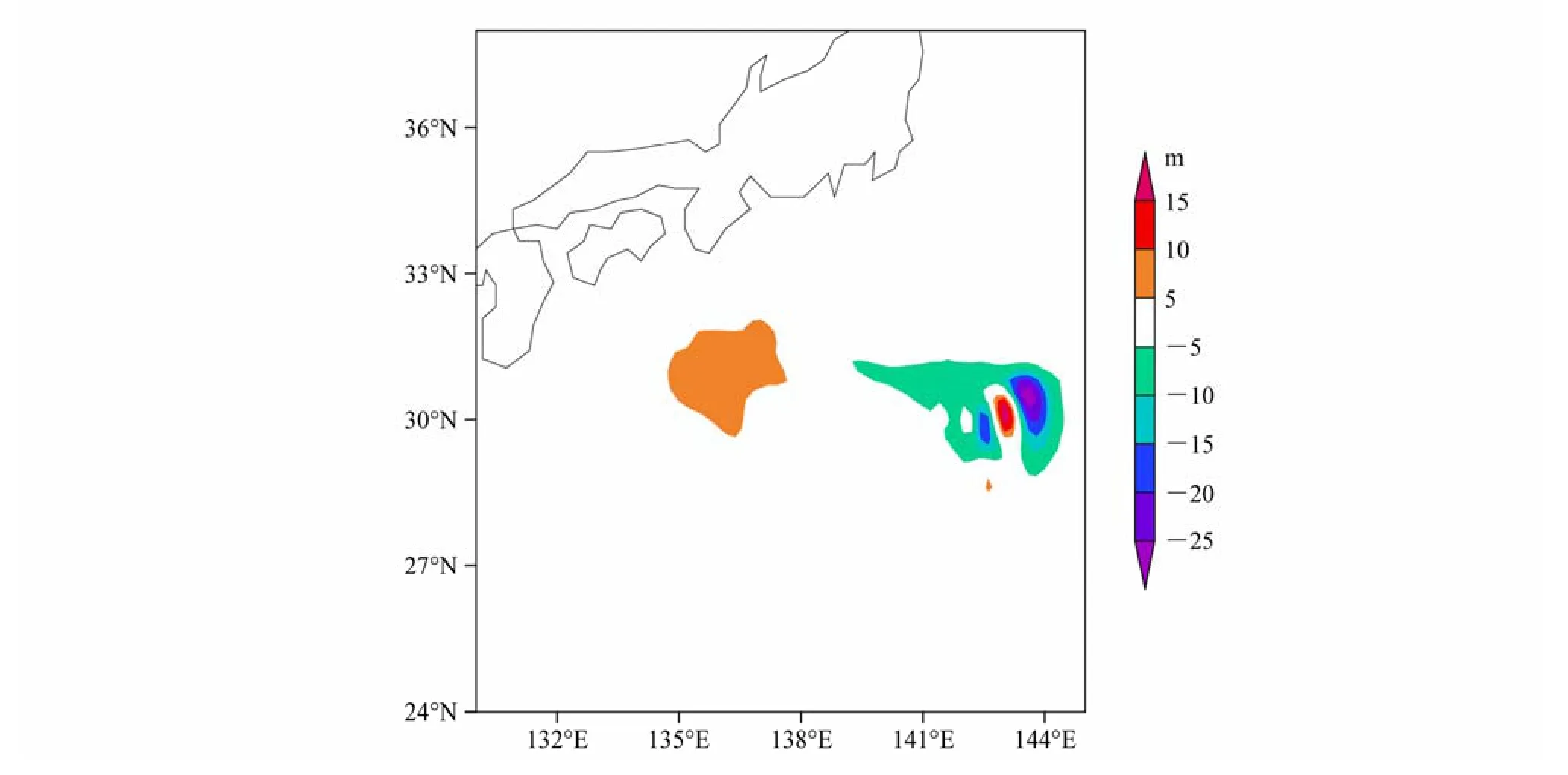
圖4 CNOP-I的上層厚度分量，單位：m。引自Wang et al.(2012)Fig.4 Upper-layer thickness (unit: m) component of CNOP-I.From Wang et al.(2012)

黑潮路徑變異對區域氣候產生重要影響（Xu et al.2010），對我國長江流域降水也具有較大影響（侍茂崇，2004）。黑潮路徑變異的可預報性研究具有重要意義。國際上關于黑潮路徑變異可預報性的研究，主要從初始誤差增長的角度進行研究（Komori et al.2003; Ishikawa et al.2004; Fujii et al.2008）。模式誤差對黑潮路徑變異預報的影響研究則很少。近年來，作者們將CNOP方法應用于黑潮路徑變異的可預報性研究，分辨了初始誤差和模式參數誤差對黑潮路徑變異預報影響的相對重要性，強調了初始誤差的作用（Wang et al., 2012）。

Wang et al.（2012）采用1.5層淺水模式計算了黑潮大彎曲路徑的 CNOP-I（圖 4）和 CNOP-P，其中CNOP-P包括參數風應力的最優擾動（CNOPTAU-P）、側向摩擦系數的最優擾動（CNOPAH-P）、界面摩擦系數的最優擾動（CNOPRI-P）和上述三個參數擾動的最優組合模態（CNOPAll-P）。計算結果表明，如果以預報時刻擾動的動能作為預報誤差的度量，那么CNOP-I所導致的預報誤差比不同參數的最優擾動導致的預報誤差大（圖5），也就是說，在黑潮路徑變異的預報中，初始誤差可能比模式參數誤差對預報結果不確定性的影響更大。具體地，由CNOP-I導致的海洋上層厚度的均方根誤差最大（圖6），并且大約在預報時刻120天時，均方根誤差開始大于均方根變化（RMS variation），這表明在預報時刻120天時，以具有CNOP-I誤差的初始場作為模式的初始場預報黑潮路徑變異時，該時刻的預報結果不在預報技巧允許的范圍內；然而當模式參數誤差為CNOPAll-P時，雖然CNOPAll-P也導致了顯著的預報誤差，但其在預報時刻210天時（遠大于120天），預報結果才開始不能被接受。也就是說，對于給定的預報時刻，初始誤差比參數誤差更容易導致海洋上層厚度的預報不可接受。

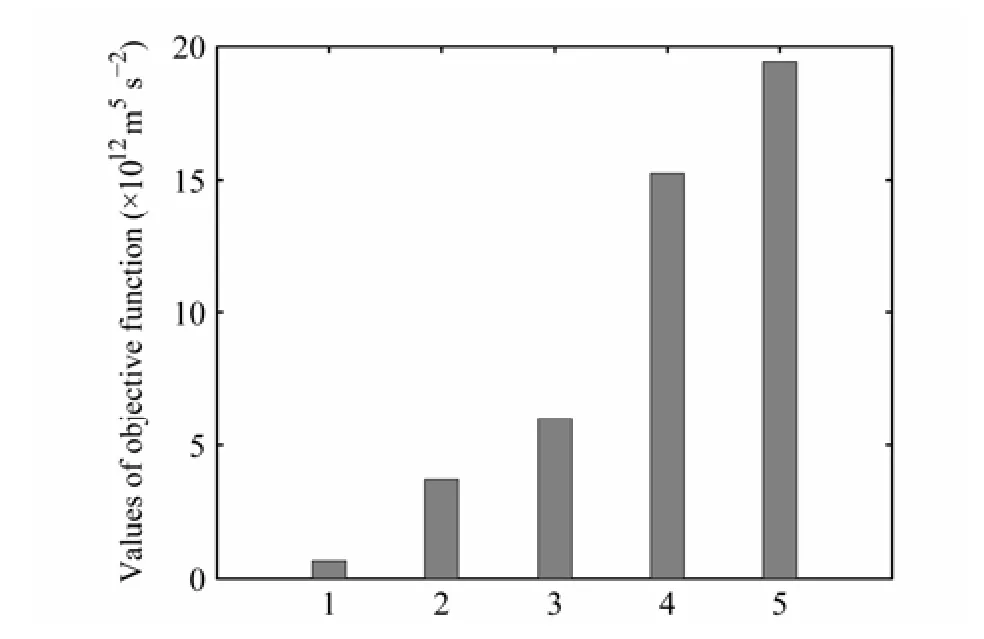
圖5 CNOP-I誤差和不同參數的最優擾動導致的預報誤差.橫軸上的數字1～5分別代表CNOPRI-P, CNOPTAU-P, CNOPAH-P, CNOPAll-P和 CNOP-I，縱軸表示橫軸所示的最優擾動導致的預報誤差（用擾動動能度量）。引自Wang et al.(2012)Fig.5 The prediction errors caused by the CNOP-I and optimal perturbations of different parameters.The numbers 1-5 in the horizontal axis denote CNOPRI-P, CNOPTAU-P, CNOPAH-P, CNOPAll-P, and CNOP-I, respectively.The vertical axis denotes the prediction errors(measured by kinetic energy of perturbations).From Wang et al.(2012)

對 1.5層淺水模式來說，初始誤差，尤其是CNOP-I誤差，比參數誤差導致更大的預報誤差，更易導致黑潮路徑變異預報結果的不確定性（圖7），因此，改進1.5層淺水模式的初始場比改進參數化方案更容易使得黑潮路徑變異的預報技巧顯著提高。那么如何改進初始場？事實上，黑潮路徑變異預報的CNOP-I誤差與ENSO預報的CNOP-I誤差有類似的特征，即CNOP-I誤差的空間模態具有明顯的局地性特征，該局地性特征使我們聯想到，可以通過目標觀測方法濾掉模式初始場中的CNOP-I誤差，進而提高黑潮路徑變異的可預報性。

5 阻塞發生的最優前期征兆和最快增長初始誤差

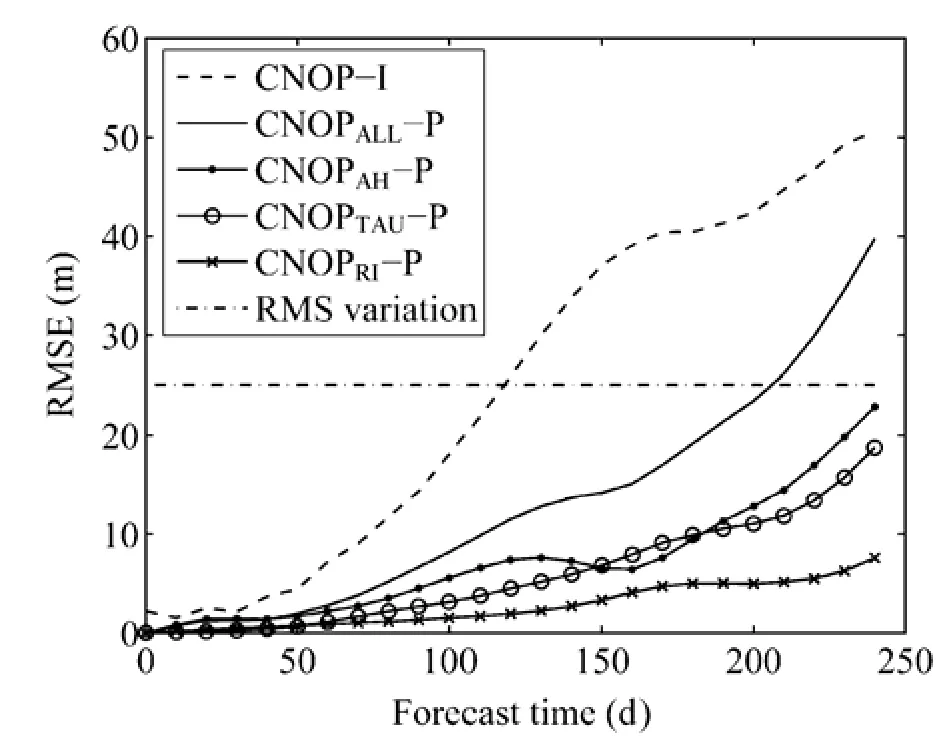
圖6 不同誤差導致的海洋上層厚度均方根誤差的時間序列。“RMS variation”表示海洋上層厚度的均方根變化，作為黑潮路徑預報誤差是否可以接受的判斷標準，該標準也被Komori et al.(2003) 用于研究黑潮路徑變異的預報時效。當均方根誤差大于“RMS variation”時，預報結果不可接受；反之，預報結果能被接受。引自Wang et al.(2012)Fig.6 Time series of root-mean-square error (RMSE) of upper-layer thickness caused by different errors.RMS variation, the root mean square variation of the upper-layer thickness, is used as a criterion determining whether the prediction results of Kuroshio path are acceptable.This criterion was also used by Komori et al.(2003) to study the time limits for the prediction of Kuroshio path variation.When RMSE is larger than RMS variation, the prediction results are unacceptable; otherwise, the predictions are acceptable.From Wang et al.(2012)

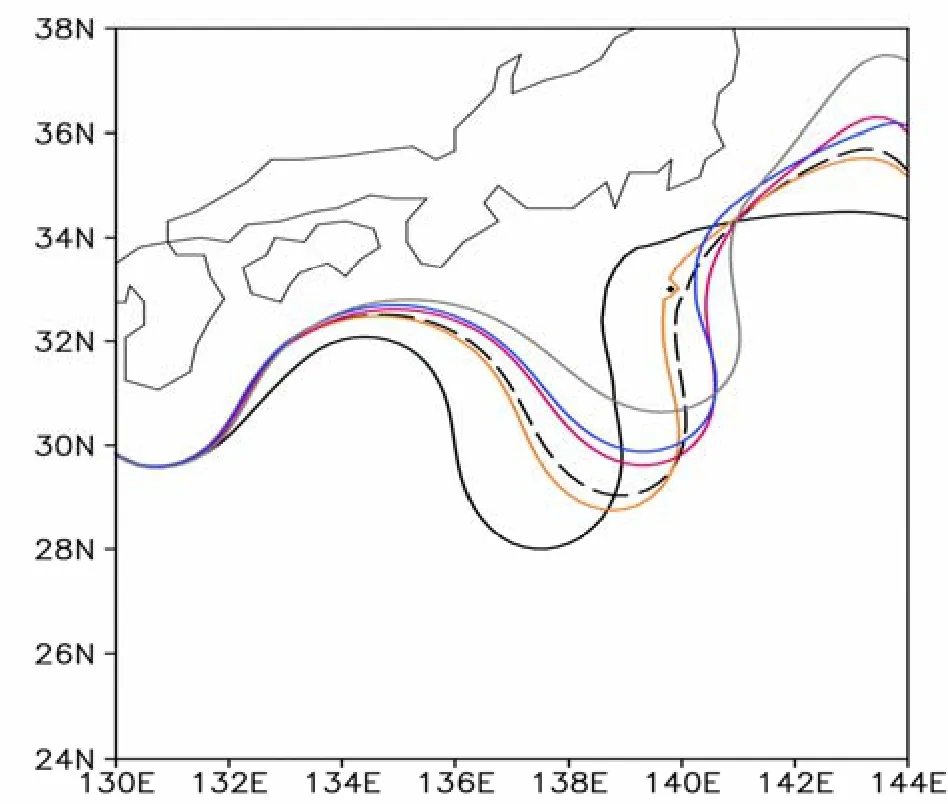
圖7 模式具有 CNOPRI-P（黃線），CNOPTAU-P（紅線），CNOPAH-P（藍線），CNOPAll-P（灰線）和CNOP-I（黑實線）誤差時，關于參考態黑潮大彎曲路徑（黑虛線）的預報結果，其中黑潮流軸由海洋上層厚度520 m等值線表征。CNOP-I誤差導致的黑潮路徑的變異比其他類型誤差更顯著。引自Wang et al.(2012)Fig.7 The reference Kuroshio large meander axis (black dashed line) and the predicted Kuroshio axes caused by CNOPRI-P (yellow line),CNOPTAU-P (red line), CNOPAH-P (blue line), CNOPAll-P (gray line), and CNOP-I (black solid line).The Kuroshio axis is described by the 520-m contour of the upper-layer thickness.CNOP-I results in larger prediction error than other types of errors.From Wang et al.(2012)

阻塞是一個典型的大尺度環流，其對區域天氣和氣候有著深遠的影響（Rex，1950）。阻塞發生對初始場的不確定性具有極端敏感性，阻塞環流轉型預報常常因此失效。所以，阻塞預報能力的提高仍然是中長期數值天氣預報研究的核心問題之一（Tibaldi and Molteni 1990; Kimoto et al.1992;Frederiksen et al.2005）。最優前期征兆（OPR）和增長最快初始誤差（OGR）是可預報性研究的兩個重要問題，許多研究基于線性近似方法研究阻塞的OPR 和OGR（Frederiksen, 1998；Molteni and Palmer,1993）。然而，線性近似方法不能充分刻畫非線性物理過程的影響，存在著較大的局限性。

考慮到線性方法的局限性，Jiang and Wang（2010）用CNOP方法，基于Liu（1994）提出的阻塞指數定義，用T21L3準地轉模式計算了最容易激發歐洲—大西洋阻塞事件發生的 OPR（圖 8）。該OPR的空間模態呈現很強的局地性特征，擾動的主要能量位于阻塞區域的上游。該 OPR主要呈現為北美大陸的波列結構，且隨高度西傾，分布于大西洋急流的北側，軸線沿著東北—西南方向。該OPR隨著時間的演變，逐漸向下游傳播并發展，最終在大西洋區域形成典型的偶極子阻塞結構。上述OPR擾動能量的發展主要來自于基本流的水平切變，斜壓調整僅起著小部分的作用。OPR擾動引發的行星尺度渦度平流向阻塞的高壓區（低壓區）輸送反氣旋渦度（氣旋渦度）（圖 9），從而促進了偶極子阻塞的發生。

Mu and Jiang（2011）同樣基于T21L3準地轉模式，選取了歐洲—大西洋區域1985年冬至1991年冬的20個個例，進一步探討了阻塞發生的OPR；而且他們又探討了阻塞預報的OGR。OGR分為兩類，一類為局部CNOP-I，記為type-1-OGR（圖9）；另一類為全局CNOP-I，記為type-2-OGR（圖10）。結果發現，OPR和OGR具有很高的相似性。以優化時間3天為例，阻塞的OPR與type-1-OGR的相似指數達到0.95，與type-2-OGR的相似指數達到―0.87。優化時間為5天時，OPR與type-1-OGR相似指數達到0.85，與type-2-OGR相似指數達到―0.69。而且，OPR和 type-1-OGR具有類似的演變行為，且都發展成為歐洲—大西洋區域的偶極子阻塞模態；type-2-OGR則隨時間的演變，發展成為上述偶極子阻塞的相反模態。也就是說，阻塞發生的 OPR與OGR不僅在初始結構上存在著相似性，在發展機理上也具有很高的相似性。

綜上所述，阻塞發生的OPR與OGR的空間模態高度相似，且具有明顯的局地性特征。這種相似性及其局地性特征啟發我們：如果在 OGR局地性特征描述的誤差大值區實施目標觀測，一方面可以消除 OGR出現的可能性，改進初始場；另一方面可以改善局地觀測網，有助于捕捉最優前期征兆的信號，從而提高我們對阻塞事件的預報能力。

6 CNOP在臺風目標觀測研究中的應用

目標觀測是指為了提高高影響天氣和氣候事件的預報技巧，在一些關鍵地區（敏感區）加強觀測（Lorenz and Emanuel, 1998）的一種觀測手段。在一系列理論和方法研究的基礎上，國際上針對熱帶氣旋、冬季風暴與溫帶氣旋等，進行了一系列外場試驗（Snyder, 1996; Langland et al., 1999;Szunyogh et al., 2000; Wu et al., 2005; Rabier et al.,2008）。這些試驗的結果表明，目標觀測能夠有效提高預報技巧。目標觀測的關鍵之一是確定敏感區。目前確定目標觀測敏感區的主要方法有兩大類，一類是線性方法（Gelaro et al., 1998; Palmer et al., 1998; Bergot, 1999; Buizza and Montani, 1999）；另一類是集合方法（Bishop and Toth, 1999）。然而這兩類方法都是基于初始擾動發展的線性性質這一假定，不能考慮非線性物理過程的影響。

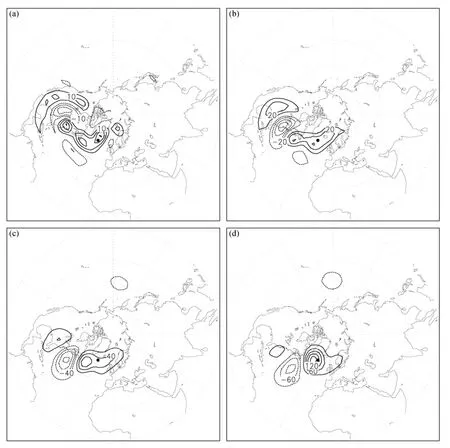
圖8 500 hPa上優化時間為3天的激發歐洲—大西洋阻塞發生的OPR及其演變（單位：gpm）。（a）第0天；（b）第1天；（c）第2天；（d）第3天。歐洲—大西洋阻塞的 OPR（見（a）圖所示）主要呈現為北美大陸的波列結構，且隨高度西傾，分布于大西洋急流的北側，軸線沿著東北—西南方向。該 OPR隨著時間的演變，逐漸向下游傳播并發展，最終在大西洋區域形成典型的偶極子阻塞結構（見（b），（c）和（d）圖所示）。引自Jiang and Wang (2010)Fig.8(a) The optimal precursor (OPR) triggering the North Atlantic–European blocking at 500 hPa with optimization time 3 days and its nonlinear evolution(gpm) with (b) leading time 1 day; (c) leading time 2 days; and (d) leading time 3 days.The OPR (see Fig.(a)) triggering the North Atlantic–European blocking presents wave trains over North America, westward with height.The disturbances, which mostly focus on the northward flanks of the corresponding Atlantic upper-level jet, take on northeast–southwest trend.With time development, it propagates downwards and develops into a typical dipole blocking over the North Atlantic–European area (see Figs.(b), (c), and (d)).From Jiang and Wang (2010)

為揭示非線性的影響，一些研究將CNOP方法應用于暴雨和臺風的目標觀測敏感區的研究中，表明了CNOP初始擾動，即CNOP-I模態具有明顯的局地性特征，嘗試將其應用于確定臺風預報的敏感區，并在敏感區減小誤差，考察其對臺風預報結果的影響。結果表明，CNOP-I敏感區較LSV敏感區更有潛力改進預報技巧（穆穆等, 2007; 譚曉偉,2009; Mu et al., 2009; Wang and Tan, 2009; Chen,2011; Qin and Mu, 2011a, 2011b; Zhou and Mu, 2011;Chen and Mu, 2012; Zhou and Mu, 2012a, 2012b）。

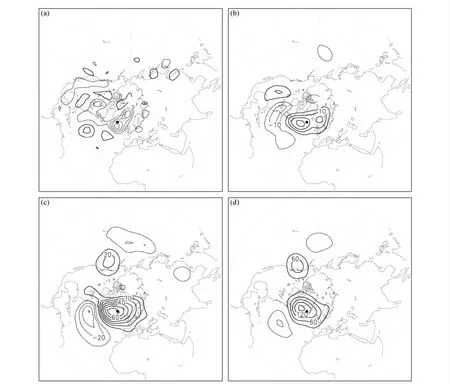
圖9 500 hPa上20個個例的type-1-OGR的合成場。（a）第0天及其在（b）第1天、（c）第2天、（d）第3天的非線性演變的合成場（單位：gpm）。引自Mu and Jiang (2011)Fig.9(a) The composite field of type-1 OGR of 20 cases at 500 hPa and its nonlinear evolution with (b) lead time 1 day, (c) lead time 2 days, and (d) lead time 3 days.From Mu and Jiang (2011)

近來，作者們進一步通過OSSE和/或OSE研究了CNOP-I確定的敏感區的有效性。Chen and Mu（2012）利用 MM5模式和 WRF模式，以臺風Longwang（2005）和 Sinlaku（2008）為例，通過OSSE試驗研究了不同方法確定的敏感區和不同類型初始誤差對臺風初值敏感區的影響以及敏感區對模式的依賴性。結果表明，敏感區內的隨機初始誤差的發展一般要大于其他隨機選擇的區域內誤差的發展；而在所有選擇的區域中，CNOP-I所識別的敏感區內的隨機誤差的發展是最大的；在同一個區域中，具有特定空間結構的初始誤差的發展一般要大于隨機誤差的發展，如 CNOP-I、singular vectors（SVs）和LSV類型的初始誤差的結構。綜合比較研究的結果，發現CNOP-I所識別的敏感區內CNOP-I類型初始誤差對預報結果不確定性的影響最大。將MM5模式計算得到的臺風預報的敏感區應用于WRF模式，結果發現由MM5模式確定的敏感區在WRF模式中也能非常有效地減小預報誤差，說明臺風預報的初值敏感區對模式（至少在MM5和WRF模式）的依賴性可能較弱。

針對上述CNOP-I確定的敏感區，Chen（2011）結合臺灣的“追風計劃”收集的下投探空資料，通過OSE試驗表明，在CNOP-I敏感區內同化目標觀測資料，各氣象要素的總擾動能量（TPE）的均方根誤差（RMSE）的減小幅度要明顯大于在隨機區域的情況。這說明在CNOP-I確定的敏感區內進行目標觀測，確實能夠有效減小臺風預報誤差。

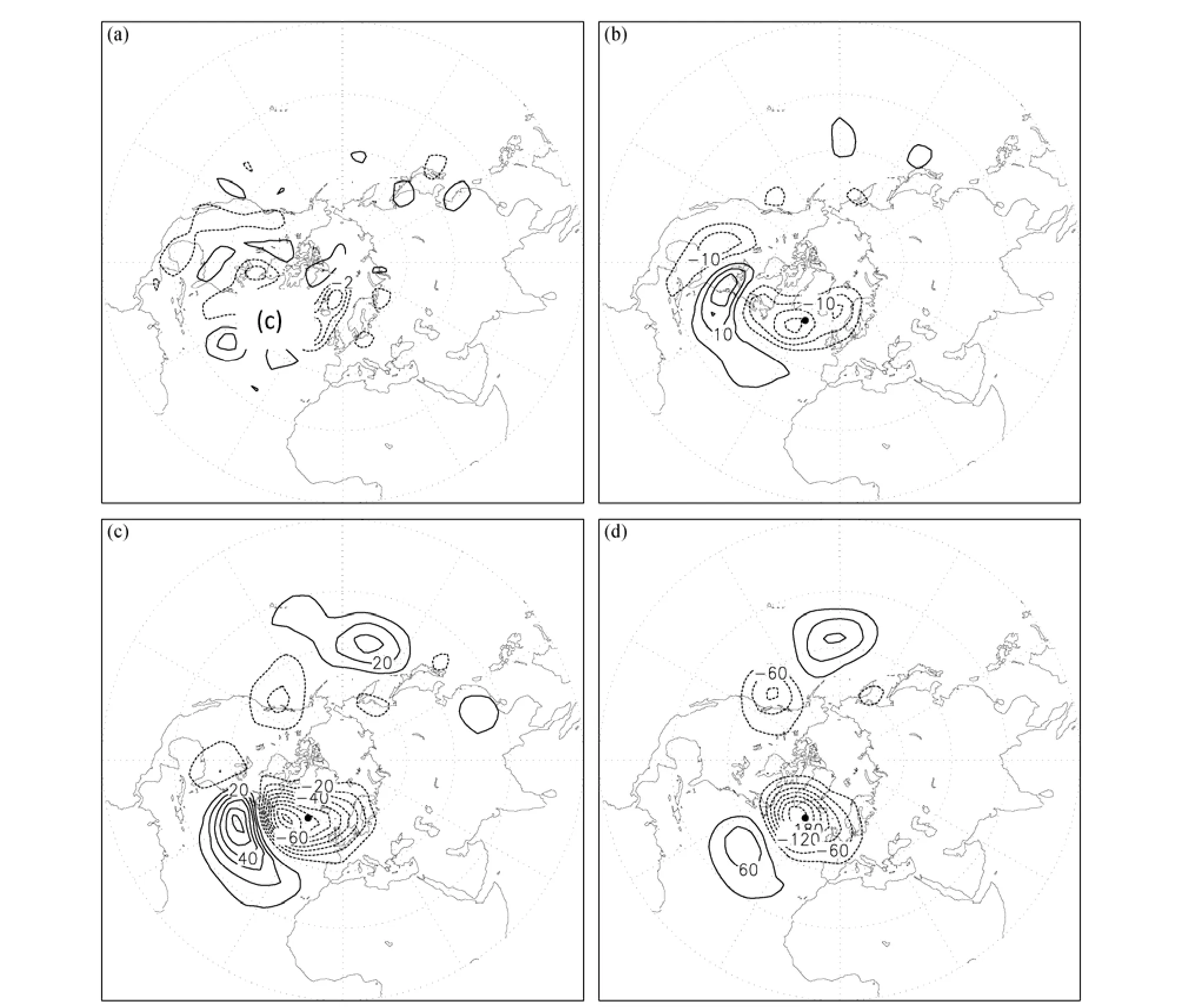
圖10 500 hPa上20個個例的type-2-OGR的合成場。（a）第0天及其在（b）第1天、（c）第2天、（d）第3天的非線性演變的合成場（單位：gpm）。引自Mu and Jiang (2011)Fig.10(a) The composite field of type-2 OGR of 20 cases at 500 hPa and its nonlinear evolution with (b) lead time 1 day, (c) lead time 2 days, and (d) lead time 3 days.From Mu and Jiang (2011)

Qin and Mu（2011b）將其應用于2009年西太平洋7個個例臺風路徑預報的研究。結果表明，選擇占全場 1%的敏感區作為目標觀測區。將同化了觀測資料后的初始場作為進行了目標觀測后改善的初始場，進行每6 h一次的路徑預報，總共預報時長為72 h。試驗結果表明：7個臺風個例中有6個個例的路徑預報得到了明顯改善（圖 11）。在CNOP敏感區內進行目標觀測，路徑預報改善程度為13%～46%，48 h路徑預報誤差平均減少89.6 km左右，驗證區內預報氣壓平均減小 7 hPa；在 SVs敏感區內進行目標觀測，改善程度僅為14%～23%；而且上述改善不僅出現在優化時間段內（24～48 h），甚至延續到72 h，臺風路徑72 h預報誤差平均減少25.9 km。這說明CNOP適應性資料同化技術可以有效地改進臺風路徑的預報技巧。

綜上，CNOP方法比其他方法更能抓住臺風預報初始誤差的敏感區域，OSEs (OSSEs) 試驗驗證了CNOP確定的敏感區在改進臺風預報技巧中的有效性。所以，用CNOP方法所識別的敏感區是有效的，通過在敏感區加密觀測或者進行資料同化，可以大大提高臺風的預報技巧。

7 討論

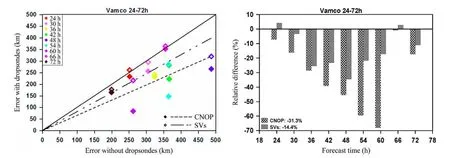
圖11 左圖：臺風環高（Vamco）在CNOP（實心菱形）和SVs（空心菱形）敏感區進行與不進行目標觀測預報路徑誤差（24～72 h）比較；右圖：路徑預報誤差減小程度。引自Qin and Mu (2011b)Fig.11 Scatter diagrams for cases Vamco (left).The y-axis represents the track forecast errors with dropsondes, and the x-axis represents those without dropsondes.Filled and empty diamonds denote the results of CNOPs and SVs, respectively.The colour of each diamond indicates the forecast time.Histograms on the right are relative differences corresponding to each case.From Qin and Mu (2011b)

CNOP方法已被應用于臺風的目標觀測問題研究，CNOP-I在確定敏感區中發揮了重要作用。上述所考察臺風個例的CNOP-I誤差具有明顯的局地性特征，即誤差主要分布在某一特定區域，該區域可能代表了目標觀測敏感區，而且作者們通過OSSEs或OSEs試驗，驗證了這一想法，即通過在敏感區進行資料同化，減小敏感區誤差，顯著改進了臺風的預報技巧。該事實告訴人們，在 CNOP-I確定的敏感區加強觀測，對于改進臺風預報技巧具有重要作用。事實上，對于本文介紹的高影響天氣和氣候事件：El Ni?o事件、黑潮路徑變異以及阻塞事件，它們的CNOP-I誤差都導致顯著的預報誤差，且誤差也主要分布在某一特定區域，具有明顯的局地性特征。考慮到臺風的目標觀測問題，我們自然聯想到，這些事件的CNOP-I呈現的局地性區域是否也代表了初始誤差敏感區，在該區域加強觀測或進行資料同化，上述事件的預報技巧是否也有顯著提高？等等問題都是需要進一步解決的問題。因此，在未來的工作中，我們有必要嘗試開展關于El Ni?o、黑潮路徑變異以及阻塞事件等高影響天氣和氣候事件的目標觀測研究。

另一方面，上述工作提到，阻塞事件的CNOP-I前期征兆和初始誤差的空間模態具有高度相似性。因此，如果阻塞事件的CNOP-I誤差局地性區域代表了阻塞預報的敏感區，那么表現在前期征兆中的同一局地性區域說明在 OGR敏感區增加觀測不僅可以提高預報技巧，而且有利于增強識別阻塞事件發生的前期信號，進而提高阻塞事件的預報技巧。也就是說，阻塞事件前期征兆和最快增長初始誤差的相似性和局地性特征可以為目標觀測的布控提供有用信息。既然前期征兆和初始誤差的相似性和局地性特征對于目標觀測有重要作用，那么發生在阻塞事件中的相似性和局地性特征是否在 El Ni?o事件、黑潮路徑變異以及臺風等高影響天氣和氣候事件中也存在？這種相似性和局地性特征是否確實能夠指導這些天氣和氣候事件的目標觀測敏感區確定，提高預報技巧？這些問題也是亟待解決的重要問題。

總之，可預報性研究是一個具有挑戰性的課題，仍然有大量的科學問題需要解決，這不僅需要學者具備扎實的氣象學知識，而且需要具備堅實的數理基礎和高性能計算機計算的能力。隨著計算機的發展以及有效的學科交叉和來自不同領域的學者的通力合作，大力提高天氣和氣候可預報性的目的將能很快變為現實。

（References）

Bergot T.1999.Adaptive observations during FASTEX: A systematic survey of upstream flights [J].Quart.J.Roy.Meteor.Soc., 125 (561):3271–3298.

Birgin E G, Martinez M J, Raydan M.2000.Nonmonotone spectral projected gradient methods on convex sets [J].SIAM J.Optim., 10 (4):1196–1211.

Bishop C H, Toth Z.1999.Ensemble transformation and adaptive observations [J].J.Atmos.Sci., 56: 1748–1765.

Buizza R, Montani A.1999.Targeting observations using singular vectors[J].J.Atmos.Sci., 56: 2965–2985.

Chen B Y.2011.Observation system experiments for typhoon Nida (2004)using the CNOP method and DOTSTAR data [J].Atmos.Oceanic Sci.Lett., 4 (2): 118–123.

Chen B Y, Mu M.2012.The roles of spatial locations and patterns of initial errors in the uncertainties of tropical cyclone forecasts [J].Adv.Atmos.Sci., 29 (1): 63–78.

Chen D, Cane M A, Kaplan A, et al.2004.Predictability of El Ni?o over the past 148 years [J].Nature, 428: 733–736.

Duan W S, Mu M, Wang B.2004.Conditional nonlinear optimal perturbation as the optimal precursors for ENSO events [J].J.Geophys.Res., 109 (D23): 4756–4768.

Duan W S, Mu M.2009.Conditional nonlinear optimal perturbation:Applications to stability, sensitivity, and predictability [J].Science in China (D), 52 (7): 884–906.

Duan W S, Liu X C, Zhu K Y, et al.2009.Exploring the initial errors that cause a significant “spring predictability barrier” for El Ni?o events [J].J.Geophys.Res., 114: C04022, doi:10.1029/2008JC004925.

Duan W, Zhang R.2010.Is model parameter error related to a significant spring predictability barrier for El-Ni?o event? Result from Theoretical Model [J].Adv.Atmos.Sci., 27: 1003–1013.

Duan W S, Wei C.2012.The spring predictability barrier for El Ni?o events and its possible mechanism results from a fully coupled model [J].Int.J.Climatol., doi:10.1002/joc.3513，in press.

Duan W S, Yu Y S, Xu H, et al.2012.Behaviors of nonlinearities modulating the El Ni?o events induced by optimal precursory disturbances [J].Climate Dyn., doi:10.1007/s00382–012-1557-z，in press.

Frederiksen J S.1998.Precursors to blocking anomalies: The tangent linear and inverse problems [J].J.Atmos.Sci., 55: 2419–2436.

Frederiksen J S, Collier M A, Watkins A B.2005.Dependence of ensemble prediction skill on blocking instability regimes [J].Tellus, 56A: 485–500.

Fujii Y, Tsujino H, Usui N, et al.2008.Application of singular vector analysis to the Kuroshio large meander [J].J.Geophys.Res., 113:C07026, doi:10.1029/2007JC004476.

Gelaro R, Buizza R, Palmer T N, et al.1998.Sensitivity analysis of forecast errors and the construction of optimal perturbations using singular vectors [J].J.Atmos.Sci., 55: 1012–1037.

Ishikawa Y, Awaji T, Komori N, et al.2004.Application of sensitivity analysis using an adjoint model for short-range forecasts of the Kuroshio path south of Japan [J].Journal of Oceanography, 60: 293–301.

Jiang Zhina, Wang Donghai.2010.A study on precursors to blocking anomalies in climatological flows by using conditional nonlinear optimal perturbations [J].Quart.J.Roy.Meteor.Soc., 136 (650): 1170–1180.

Kimoto M, Mukougawa H, Yoden S.1992.Medium-range forecast skill variation and blocking transition: A case study [J].Mon.Wea.Rev., 120:1616–1627.

Komori N, Awaji T, Ishikawa Y, et al.2003.Short-range forecast experiments of the Kuroshio path variabilities south of Japan using TOPEX/Poseidon altimetric data [J].J.Geophys.Res., 108 (C1): 3010,doi:10.1029/2001JC001282.

Langland R H, Toth Z, Gelaro R, et al.1999.The North Pacific Experiment(NORPEX-98).Targeted observations for improved North American weather forecasts [J].Bull.Amer.Meteor.Soc., 80: 1363–1384.

Liu D C, Nocedal J.1989.On the limited memory BFGS method for large scale optimization [J].Math.Program., 45 (3): 503–528.

Liu Q.1994.On the definition and persistence of blocking [J].Tellus, 46 (3):286–298.

Lorenz E N.1965.A study of the predictability of a 28-variable atmospheric model [J].Tellus, 17: 321–333

Lorenz E N, Emanuel K A.1998.Optimal sites for supplementary observation sites: Simulation with a small model [J].J.Atmos.Sci., 55:399–414.

Molteni F, Palmer T N.1993.Predictability and finite-time instability of the northern winter circulation [J].Quart.J.Roy.Meteor.Soc., 119: 269–198.

Moore A M, Kleeman R.1996.The dynamics of error growth and predictability in a coupled model of ENSO [J].Quart.J.Roy.Meteor.Soc., 122: 1405–1446

Mu M, Duan W S, Wang B.2003.Conditional nonlinear optimal perturbation and its applications [J].Nonlin.Processes Geophys., 10:493–501.

Mu M, Sun L, Henk D A.2004.The sensitivity and stability of the ocean’s thermocline circulation to finite amplitude freshwater perturbations [J].J.Phys.Oceanogr., 34: 2305–2315.

穆穆, 王洪利, 周菲凡.2007.條件非線性最優擾動方法在適應性觀測研究中的初步應用 [J].大氣科學, 31 (6): 1102–1112. Mu Mu, Wang Hongli, Zhou Feifan.2007.A preliminary application of conditional nonlinear optimal perturbation to adaptive observation [J].Chinese Journal of Atmospheric Sciences (in Chinese), 31 (6): 1102–1112.

Mu M, Duan W S, Wang B.2007a.Season-dependent dynamics of nonlinear optimal error growth and El Ni?o-Southern Oscillation predictability in a theoretical model [J].J.Geophys.Res., 112: D10113,doi:10.1029/2005JD006981.

Mu M, Xu H, Duan W S.2007b.A kind of initial errors related to “spring predictability barrier” for El Ni?o events in Zebiak-Cane model [J].Geophys.Res.Lett., 234: L03709, doi:10.1029/2006GL027412.

Mu M, Zhou F F, Wang H H.2009.A method for identifying the sensitive areas in targeted observations for tropical cyclone prediction: Conditional nonlinear optimal perturbation [J].Mon.Wea.Rev., 137: 1623–1639.

Mu M, Duan W S, Wang Q, et al.2010.An extension of conditional nonlinear optimal perturbation and its applications [J].Nonlin.Processes Geophys., 2010, 17: 211–220.

Mu M, Jiang Z N.2011.Similarities between optimal precursors that trigger the onset of blocking events and optimally growing initial errors in onset prediction [J].J.Atmos.Sci., 68: 2860–2877.

Palmer T N, Gelaro R, Barkmeijer J, et al.1998.Singular vectors, metrics,and adaptive observations [J].J.Atmos.Sci., 55: 633–653.

Powell M J D.1982.VMCWD: A FORTRAN subroutine for constrained optimization [R].DAMTP Report 1982/NA4, University of Cambridge,England.

Qin X H, Mu M.2011a.A study on the reduction of forecast error variance by three adaptive observation approaches for tropical cyclone prediction[J].Mon.Wea.Rev., 139: 2218–2232.

Qin X H, Mu M.2011b.Influence of conditional nonlinear optimal perturbations sensitivity on typhoon track forecasts [J].Quart.J.Roy.Meteor.Soc., 138: 185–197.

Rabier F, Gauthier P, Cardinali C, et al.2008.An update on THORPEX-related research in data assimilation and observing strategies [J].Nonlin.Processes Geophys., 15: 81–94.

Rex D F.1950.Blocking action in the middle troposphere and its effects upon regional climate.I: An aerological study of blocking action [J].Tellus, 2: 196–211.

Riviere O, Lapeyre G, Talagrand O.2008.Nonlinear generalization of singular vectors: Behavior in a baroclinic unstable flow [J].J.Atmos.Sci.,65: 1896–1911.

Samelson R G, Tziperman E.2001.Instability of the chaotic ENSO: The growth-phase predictability barrier [J].J.Atmos.Sci., 58: 3613–3625.

侍茂崇.2004.物理海洋學 [M].濟南: 山東教育出版社.462pp.Shi Maochong.2004.Physical Oceanography (in Chinese) [M].Jinan:Shandong Education Press, 462pp.

Snyder C.1996.Summary of an informal workshop on adaptive observations and FASTEX [J].Bull.Amer.Meteor.Soc., 77: 953–961.

Szunyogh I, Toth Z, Morss R E, et al.2000.The effect of targeted dropsonde observations during the 1999 Winter Storm Reconnaissance Program [J].Mon.Wea.Rev., 128: 3520–3537.

譚曉偉.2009.CNOP新算法研究及其在目標觀測中的應用檢驗 [D].中國科學院大氣物理研究所博士學位論文, 99pp.Tan Xiaowei.2009.Studies on new algorithms to obtain CNOP and their applications in the targeting observations [D].Ph.D.dissertation (in Chinese), Institute of Atmospheric Physics, Chinese Academy of Sciences, 99pp.

Tennekes H.1991.Karl Popper and the accountability of numerical forecasting [C] // New Developments in Predictability.ECMWF Workshop Proceedings, ECMWF, Shinfield Park, Reading UK.

Terwisscha van Scheltinga A D.2007.Data assimilation with implicit ocean models [D].Ph.D.dissertation.Institute for Marine and Atmospheric research, Utrecht University, Utrecht, the Netherlands, 119pp.

Thompson P.1957.Uncertainty of the initial state as a factor in the predictability of large scale atmospheric flow patterns [J].Tellus, 9: 275–295

Tibaldi S, Molteni F.1990.On the operational predictability of blocking [J].Tellus, 42A: 343–365.

Wang B, Fang Z.1996.Chaotic oscillation of tropical climate: A dynamic system theory for ENSO [J].J.Atmos.Sci., 53: 2786-2802.

Wang B, Tan X.2009.A fast algorithm for solving CNOP and associated target observation tests [J].Acta Meteorologica Sinica, 23: 387–402.

Wang Q, Mu M, Dijkstra H A.2012.Application of the conditional nonlinear optimal perturbation method to the predictability study of the Kuroshio large meander [J].Adv.Atmos.Sci., 29 (1): 118–134.

Wu X G, Mu M.2009.Impact of horizontal diffusion on the nonlinear stability of thermohaline circulation in a modified box model [J].J.Phys.Oceanogr., 39: 798–805.

Wu C C, Lin P H, Aberson S, et al.2005.Dropwindsonde observations for typhoon surveillance near the Taiwan region (DOSTAR): An overview [J].Bull.Amer.Meteor.Soc., 86: 787–790.

Xu H, Tokinaga H, Xie S P.2010.Atmospheric effects of the Kuroshio large meander during 2004–05 [J].J.Climate., 23: 4704–4715.

Yu Y S, Duan M S, Xu H, et al.2009.Dynamics of nonlinear error growth and season-dependent predictability of El Ni?o events in the Zebiak-Cane model [J].Quart.J.Roy.Meteor.Soc., 135: 2146–2160.doi:10.1002/qj.526.

Yu Y S, Mu M, Duan W S.2012a.Does model parameter error cause a significant spring predictability barrier for El Ni?o events in the Zebiak-Cane model? [J].J.Climate., 25: 1263–1277.

Yu Y S, Mu M, Duan W S, et al.2012b.Contribution of the location and spatial pattern of initial error to uncertainties in El Ni?o predictions [J].J.Geophys.Res.-Ocean, 117: C06018, doi:10.1029/2011JC007758.

Zhou F F, Mu M.2011.The impact of verification area design on tropical cyclone targeted observations based on the CNOP method [J].Adv.Atmos.Sci., 28 (5): 997–1010.

Zhou F F, Mu M.2012a.The impact of horizontal resolution on the CNOP and on its identified sensitive areas for tropical cyclone predictions [J].Adv.Atmos.Sci., 29 (1): 36–46.

Zhou F F, Mu M.2012b.The time and regime dependences of sensitive areas for tropical cyclone prediction using the CNOP method [J].Adv.Atmos.Sci., doi:10.1007/s00376-012-1174-0.

Zhu C Y, Byrd R H, Lu P H, et al.1997.Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization [J].ACM T.Math.Software, 23 (4): 550–560.