分數階神經網絡控制器自頂向下優化方法

李文，亓芳，聶冰

(1.大連交通大學 軟件學院，遼寧 大連 116028;2.大連交通大學 電氣信息學院，遼寧 大連 116028)*

0 引言

目前，神經網絡理論與應用研究已經廣泛應用于專家系統、工業控制以及模式識別等領域.采用誤差逆傳播算法訓練的多層前饋網絡BP網絡是應用最廣泛的神經網絡模型之一.然而，BP神經網絡的結構通常根據經驗選取，結構單一，無法根據系統的實際情況而實時調整網絡結構，缺乏科學性.

本文設計了基于BP神經網絡的分數階PIλ控制器，并提出自頂向下優化BP神經網絡的方法，系統結構如圖1所示.實驗結果表明通過這種優化神經網絡結構的方法，刪除冗余節點，精簡網絡結構，增強了BP神經網絡的適應能力［4］.

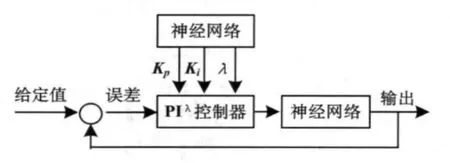
圖1 基于神經網絡的分數階PIλ控制器框圖

1 分數階PIλ控制器的設計［1］

分數階PIλ控制器是由整數階控制系統擴展而來，其分數階控制器的傳遞函數表達式為:

式中，KP、KI分別為控制器的比例系數和積分系數;λ＞0是分數階控制器的積分階次，可表示為任意實數.

分數階控制器具有無限階次，需要對分數階微積分算子sλ進行離散化［7］.本文采用Tustin生成函數和連分式方法(CFE)結合對分數階控制器進行離散化，三階展開得到離散表達式為:

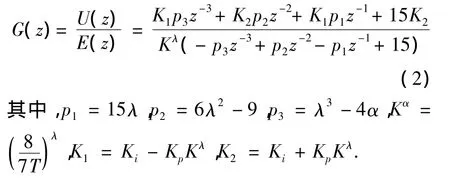
則U(z)時間域的離散表達式為:

2 分數階PIλ控制器自頂向下優化神經網絡的方法

本文采用BP神經網絡對PIλ控制器中的KP、KI和λ三個參數進行調節，利用自頂向下的方法優化網絡的結構，提高神經網絡的性能.

2.1 經典BP神經網絡學習算法［3］

BP神經網絡是一種按照誤差算法訓練的多層前饋網絡，廣泛的應用于各種工業控制領域.在BP神經網絡中，輸入層各神經元接收輸入信息，傳遞給隱層各神經元;隱層是內部信息處理層，負責信息變換;最后隱層傳遞到輸出層各神經元的信息，經進一步處理后，完成一次學習的正向傳播處理過程，由輸出層向外界輸出信息處理結果.當實際輸出與期望輸出不符時，進入誤差的反向傳播階段.誤差通過輸出層，按誤差梯度下降的方式修正各層權值，向隱層、輸入層逐層反傳.周而復始的信息正向傳播和誤差反向傳播過程，是各層權值不斷調整的過程，也是神經網絡學習訓練的過程.該循環過程一直進行，直到網絡輸出的誤差減少到可以接受的程度，或者達到預先設定的學習次數為止.在文獻［3］和［6］中對經典BP算法作了詳細的介紹.

2.2 自頂向下優化BP神經網絡的條件

在分數階PIλ控制器中，輸入層和輸出層節點數是由系統本身的特點決定的.本系統選擇輸入層節點四個:X=(e，e-1，ce，ce-1);輸出層節點三個:Y=(KP，KI，λ).而隱層層數和維數的選擇決定了網絡的規模.如果選擇的神經網絡規模過大，則神經網絡逼近能力過剩;選擇的神經網絡規模過小，則神經網絡的逼近能力不足，在學習的過程中不可能收斂.Robert Hecht Nielson等人指出:只有一個隱層的神經網絡，只要隱節點足夠多，就可以以任意精度逼近一個非線性函數［4］.因此，隱層節點數的確定是神經網絡設計的重要內容，構造一個可變結構的網絡，根據系統的實際情況自學習的調整結構，得到隱層節點數適合的神經網絡.

本系統根據節點之間的相關性采用自頂向下優化神經網絡的方法確定隱層節點數.自頂向下設計方法的核心思想是先構造一個足夠大的網絡，通過在訓練中刪除或合并某些節點或權值達到精簡結構的目的［5］.首先計算隱節點輸出之間的相關性，然后將相關性較大的冗余隱節點合并，最終確定合適的神經網絡隱節點個數.

在訓練神經網絡的過程中，計算兩個隱節之間的相關性為:

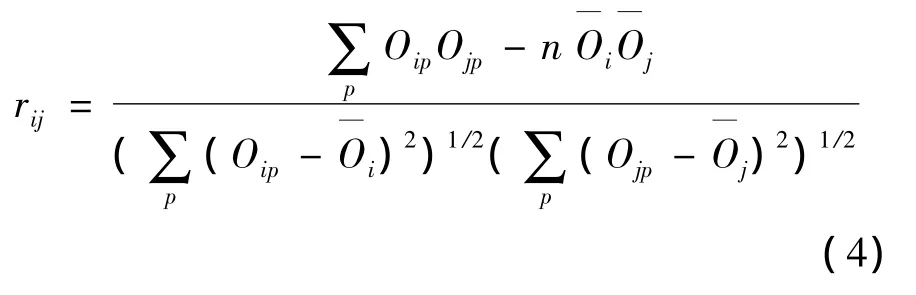
式中，Oip和Ojp是i和j兩個隱節點對第P個樣本的輸出，輸出均值分別為

對于任意的隱節點a的輸出標準差為:s2a=

當兩個節點相關性|rij|越接近1，說明這兩個節點的線性相關性越高，存在冗余的節點需要合并;當某個節點的輸出標準差較小時，則該隱節點對網絡訓練作用較小，可以刪減.

根據上述計算公式，自頂向下優化神經網絡的基本原則為:

(1)如果隱層兩個節點相關性|rij|≥α1，且輸出標準差s2i＞ α2，s2j＞ α2，則隱節點i和j可以合并.其中α1和α2為規定的下限值，一般α1取0.8 ～ 0.9，α2取0.001 ～ 0.01;

(2)若某節點的輸出標準差sa≤α2，則說明節點a的作用較小，可以將其刪除.

2.3 自頂向下優化BP神經網絡的方法

由上述合并條件，結合經典BP神經網絡學習算法，得到自頂向下優化神經網絡算法的步驟如下:

(1)網絡初始化:確定系統輸入層、輸出層和隱層節點數;隨機初始權值;學習系數;合成時刻誤差ε1;目標誤差ε2;節點相關性閥值α1;輸出標準差閥值α2;初始學習步數k=1;

(2)采用BP算法進行學習，同時計算所有隱節點輸出序列;

(3)判斷誤差是否滿足合成、終止學習條件:如果當前訓練誤差值E＞ε1，K=K+1轉到步驟(2);如果 ε1≥E≥ ε2，轉到步驟(4);E ＜ ε2，則終止學習;

(4)計算各隱節點輸出序列的標準差和相關性;

(5)檢查并合并隱節點:如果隱節點i和隱節點j相關系數滿足|rij|≥ α1，且s2i＞ α2，s2j＞ α2，則對隱節點(i，j)進行合并;如果某個隱節點輸出標準差滿足s2i＜ α2，則刪除該節點，K=K+1，轉到步驟(2).

3 應用實例

以二階系統 Y(t)= Y_set(1-e(-t/ξωn)*sinωdt)為例，取合成時訓練誤差 ε1=0.03，目標誤差ε2=3*10-4，節點相關性閥值α1=0.9，輸出標準差閥值α2=0.01，初始權值產生范圍［-1，1］，初始網絡結構為4-10-3網絡.經過自頂向下方法優化后，本神經網絡結構優化為4-2-3網絡.停止學習后，輸出序列相關性高于閥值兩個隱節點合并，其部分合并隱節點的輸出序列如圖2所示.圖3顯示了該系統的輸出響應曲線.圖4所示為訓練樣本的學習曲線，在每次合并隱節點后，神經網絡的訓練誤差并沒有發生明顯變化.

圖2 高度相關的節點輸出序列

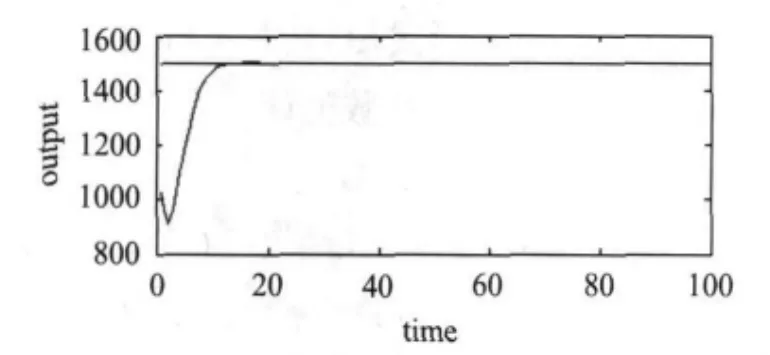
圖3 系統輸出響應曲線

圖4 樣本學習曲線

4 結論

本文提出了分數階PIλ控制器中優化BP神經網絡的方法，詳細介紹了自頂向下的神經網絡優化算法.結果表明，自頂向下的優化神經網絡方法可以通過合并某些相關性較大的隱節點、刪除對網絡影響較小隱節點保證神經網絡在合并、刪除節點后特性不變，從而達到了簡化網絡結構的目的.

［1］聶冰，趙慧敏，郭永香，等.交流電機調速系統的分數階 PIλ控制［J］.大連交通大學學報，2012，33(2):84-86.

［2］趙慧敏，李文，鄧武.基于神經網絡的分數階PIα控制器的設計與實現［J］.大連交通大學學報，2008，29(1):63-67.

［3］陳東洋，張新政.可變結構神經網絡在未來水質參數預測中的應用［J］.科學技術與工程，2008，8(6):1577-1604.

［4］劉光中，李曉峰.人工神經網絡BP算法的改進和結構的自調整［J］.運籌學學報，2001，5(1):81-88.

［5］魏海坤.神經網絡結構設計的理論與方法［M］.北京:國防工業出版社，2005:125-141.

［6］李廣軍，張晶，曾安平.基于BP神經網絡的PID控制器研究［J］.計算機仿真，2009，26(9):128-131.

［7］CHEN YANGQUAN.A new discretization method for fractional order differentiators via continued fraction expansion［C］.2003 ASME International Design Engineering Technical Conferences，September 2-6，2003，Chicago，USA，2003:1-9.