微壓力彈簧性能自動測試裝置的設計與實現

王亭嶺 周芬芳 熊軍華 陳建明 沈媛雪

(華北水利水電學院電力學院1，河南 鄭州 450011;中州大學信息管理中心2，河南 鄭州 450044)

0 引言

能源危機促進了物質勘探行業的快速發展。在石油勘探、地震測量中，大量使用地震檢波器來采集地層傳遞過來的電磁波。因此，地震檢波器的測量精度是決定物質勘探成敗的關鍵所在。地震檢波器中對稱彈簧的性能是影響測量精度的主要因素，而提高地震檢波器測量精度的有效方法是采用適宜的檢測手段。目前，國內生產地震檢波器的很多企業都缺少必要的檢測手段，導致產品的誤差較大且重復性不好。

本文通過分析彈簧勁度系數的非線性，找出最佳匹配組，滿足兩片彈簧勁度系數之和為常數的要求。文中研制的微壓力彈簧性能自動測試裝置能對多批次彈簧性能實現動態快速自動測量，并能測量出彈簧在彈性范圍內的任意位置所受到的彈力值，根據彈力與位移的對應關系計算出任意位置的勁度系數。

1 系統結構組成

整個系統由自動測試裝置和上位機監控與分析程序兩部分組成。自動測試裝置主要包括機械結構、傳動機構、檢測環節和主控單元。系統結構如圖1所示。

圖1 系統結構圖Fig.1 Structure of the system

步進電機和直線導軌垂直安裝，壓力模塊水平安裝。支架與各部分通過螺栓固緊減少振動，避免機械傳動時引入偏移誤差[2]。

圖1中，機械結構設計的關鍵是直線導軌的滑塊如何推動圓形轉盤自動放置彈簧。測試裝置位移測量控制策略采用雙閉環控制:內環為增量編碼器檢測角位移，用于消除步進電機失步帶來的誤差;外環為磁柵尺檢測直線位移，用于消除導軌絲杠間隙及機械傳動帶來的誤差。內環實現快速位置標定，外環對重復性誤差進行校正。

系統檢測與控制電路原理圖如圖2所示。

圖2 檢測與控制電路原理框圖Fig.2 Schematic diagram of the detection and control circuit

圖2中，主控單元采用TI公司的16位低功耗微控制器MSP430，用于控制步進電機驅動器[3]。步進電機驅動器選用美國海頓公司的細分型高性能步進電機驅動器DCM4010，步進電機為兩相混合式步進電機。在內環檢測回路中，增量式編碼器套緊在步進電機驅動軸上，經過四細分辨向電路將角位移所對應的四倍脈沖數據送入主控單元[4]。外環檢測回路中的磁柵尺經四細分辨向電路將四倍頻的脈沖送入主控單元，確定導軌移動的直線位移。

系統采用Verilog HDL硬件描述語言編程實現四細分辨向計數電路功能，并將整個電路布線到FPGA芯片中;利用FPGA中，同步D觸發器的延時特性及一定的與邏輯，對A、B信號的邊沿進行提取，以實現信號的四細分。四細分信號通過邏輯判斷得到計數器所需的加減計數信號，計數器對加減計數信號進行可逆計數，完成四細分辨向計數電路功能。壓力傳感器通過24位A/D轉換器CS5532，將采樣的壓力數據送入控制核心，通過數字濾波實現彈力檢測。主控單元通過MAX3232轉換芯片將TTL邏輯電平轉換為RS-232C邏輯電平，實現與上位機的串行通信。位置傳感器選用光電開關，用以限定導軌滑塊的移動范圍，避免導軌滑塊堵死。

2 步進位移誤差校準

彈簧片加工誤差的存在要求對勁度系數做精準測量。根據胡克定律，可繪制測量位移與壓力的對應勁度系數特性曲線。彈簧長度為(2±0.1)mm，受力小于10 gf(1 kgf=9.8 N)，檢測儀測量的位移誤差小于5 μm、壓力誤差小于2 mgf(1 kgf=9.8 N)。胡克定律描述的是材料在彈性變形范圍內力與變形的關系:

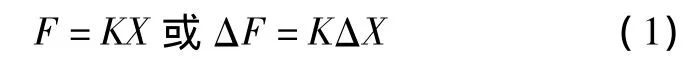
式中:K為勁度系數，N/m;X為彈性形變，m。在對稱彈簧的彈性變形范圍內，求出任意兩點的位移與壓力值，即可計算出勁度系數。嚴格意義上講，由于制造彈簧的材質是非均勻的，材料內各點受力后將有不同的彈性效應[5]。為了能更好地分析彈簧制造過程中引入誤差的影響，需要對不同批次的彈簧進行多點測量，并繪制出勁度系數特性曲線。

選用兩相混合式步進電機，步距角為1.8°，導軌絲杠的螺距為2.54 mm，不接細分驅動器時，電機步進一步的直線距離為12.7 μm。

此時，步進精度不滿足系統要求，需要增加步進電機細分驅動器。當傳動機構沒有接細分驅動器調試系統時，電機啟動及運行期間振動較明顯，編碼器的輸出脈沖受干擾較大;當傳動機構接細分驅動器時，將細分等級調到16細分，則可明顯改善電機振動現象。16細分步進一步對應直線距離為0.794 μm，當細分等級調到64細分時，理論上步進電機步進一步對應的直線距離為0.198 μm。但實際上由于步進電機控制是開環系統，在高細分等級情況下會出現失步現象，因此根據主控單元輸出脈沖多少來計算步進的位移會使測試距離存在較大的誤差。

細分驅動器的主要作用是抑制電機低頻時的振動，同時提高步進精度[6]。當細分等級為16細分以上時，精度提高不明顯，這是因為步進電機是由細分驅動器精確控制其相電流來實現細分控制的[7]。

步進電機開環控制系統通過增加編碼器來構成反饋環節，實現閉環控制。編碼器的脈沖輸出能真實反映步進的角位移。圖1中的角位移反饋信號選用400線的增量式編碼器進行檢測。編碼器輸出脈沖經四細分辨向電路送入主控單元處理，單個脈沖所對應的直線距離為:

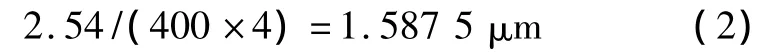
此時，步進精度由編碼器最小分辨率決定。編碼器測量的是角位移，由于導軌絲杠的間隙誤差對角位移轉換為直線位移影響較大，只有增加直線位移檢測環節，才能有效提高測量精度。系統設計的位移測量精度小于5 μm，試驗初期很難滿足這一要求。分析發現:造成誤差的主要因素與磁柵尺本身精度及安裝方式有關。磁柵尺對每段位移測量的誤差值都不同，表現為測量誤差的非線性。因此，必須對誤差的非線性進行補償。文獻[8]提出了光柵尺分段線性誤差補償算法。大量重復性試驗發現，標定的標準值及相應區間的斜率ki受測量時的環境因素影響較大，不利于程序查表計算。

文獻[9]提出了光柵位移測量系統的誤差自修正方法，試驗采用光電開關作為多個絕對零位信號的位置檢測。由于光電開關進行位置檢測時自身存在誤差，因此此方法將引入多個零位測量誤差。系統選用應差距離為25 μm的光電位置傳感器作為零位置標定，采用臨界法標定零位，具體實現步驟如下。

①判斷滑塊是否遮住光電位置傳感器，如果遮住，則滑塊后退，直到主控單元檢測的光電位置傳感器輸出高電平，高電平即為無遮擋狀態;

②無遮擋時驅動電機前進，當檢測到低電平時立即停止，并將編碼器初值清零;

③驅動步進電機后退，并對編碼器反饋的脈沖計數，當檢測到高電平時立即停止;

④若脈沖計數值小于設定值，將編碼器初值清零，并將此時的位置作為參考零點;

⑤若脈沖計數值大于設定值，重復上述操作，直至滿足條件為止。

當臨界法中的設定值為8時，循環4次左右即可標定零位;當設定值小于5時，系統振動，無法標定零點。若設定值為8，則有:

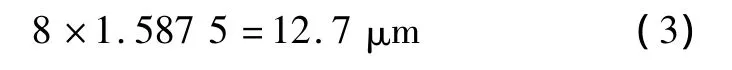
由此可知，零位信號的檢測將引入誤差。因此，引入多個絕對零位信號對提高精度不利。自動測試裝置內環選用增量編碼器檢測角位移，以實現快速定位;外環選擇磁柵尺測量直線位移，以補償角位移轉換過程中的誤差，并對重復性誤差進行校正。

磁柵尺選用德國SIKO的MB500，分辨率為5 μm，經四細分辨向電路處理后，分辨率提高了4倍。增量式光電編碼器結構簡單，價格上比絕對式編碼器占明顯的優勢，自動測試裝置角位移檢測選用400線的增量式編碼器。

3 壓力誤差分析與修正

壓力傳感器無壓力時，輸出電壓為2.0 mV;載荷為10 gf(1 kgf=9.8 N)時，輸出電壓為 2.69 mV。試驗首先選用16位的A/D轉換器AD7705，參考電壓為2.5 V，測量方式選擇單極性測量方式，增益選為增大值的128倍[10]，則 AD7705的分辨率為:

在增益設置為128倍時，壓力傳感器差分輸入信號上的干擾同時被放大。保持載荷為10 gf(1 kgf=9.8 N)不變，在連續采樣10次的16位數據中，低3位為隨機變化值，受干擾嚴重，通過數字濾波也只能把干擾降低一倍。2位隨機值使精度降低了4倍，最后壓力誤差只能控制在18 mgf(1 kgf=9.8 N)以下，無法滿足精度要求。

自動測試裝置對精密度要求很高，而對正確度要求不是很嚴格，即對彈簧勁度系數的一致性要求很高。為了解決壓力傳感器無法消除零點漂移的問題，選用高精度的A/D轉換器是行之有效的方法。

本系統以24位串行A/D轉換器CS5532為壓力采集處理電路的核心。參考電壓為2.5 V，測量方式選擇單極性測量方式，增益選為16倍，則CS5532的分辨率為:

考慮增益對干擾信號的放大影響，且CS5532采樣后的數字量仍然無法保證低3位穩定不變，若將精密度控制在1 mgf(1 kgf=9.8 N)以下，必須采用數字濾波算法。本設計采用去極值平均濾波算法，大大提高了測試裝置的精度。去極值平均濾波算法的實現過程為:首先主控單元連續讀10次取CS5532的采樣值并將其累加求和;然后找出其中的最大值與最小值并從累加和中減去;最后按8個采樣值求平均，得到有效采樣值，供系統使用。

4 控制程序設計

自動測試裝置在滿足高精度測量的同時，還要兼顧彈簧性能測試的效率。因此，裝置的工作方式設置為自動和手動兩種形式。手動方式可以進行微調和校準。自動方式下共有模式0、模式1、模式2這3種。

系統上電時默認為自動工作狀態。自動方式下的模式0每次檢測3個點，并算出2個勁度系數K值，用于快速檢測;模式1每次檢測6個點，并算出5個勁度系數K值，用于分批次檢測;模式2每次檢測11個點，并算出10個勁度系數K值，用于加工工藝分析。磁柵尺輸出脈沖與編碼器輸出脈沖經四細分辨向電路送入MSP430中斷I/O口，通過觸發中斷完成脈沖計數。系統中還使用了其他類型的中斷，如定時器中斷顯示信息等。

為了不影響脈沖計數，設置脈沖觸發中斷的優先級為最高，避免其他中斷源嵌套。

自動測試裝置主程序流程圖如圖3所示。

圖3 主程序流程圖Fig.3 Flowchart of the main program

5 試驗結果

試驗測試時，首先標定零點確定對應的壓力值，然后標定步進固定的距離(程序設定步進100步)并讀取對應的壓力值。計算壓力增量和位移增量，即可計算出勁度系數。對隨機選出的彈簧進行6次重復測量所獲取的試驗數據如表1所示。

表1 重復測量壓力數據Tab.1 Pressure data of repeated measurements

根據表1所算出的壓力平均值為1.697 gf(1 kgf=9.8 N)，最大偏差為 1.702 － 1.688=0.014 gf，相對偏差為0.014/1.697=0.825%，精度為 0.014/5=0.28%。大量重復測試數據顯示，位移誤差小于3 μm，壓力誤差小于 1 mgf(1 kgf=9.8 N)，最終得出勁度系數精度等級為0.5級。

6 結束語

本文設計的自動測試裝置主要用于對精密彈簧的性能進行定量檢測，通過測量壓力與位移的對應關系實現對彈簧彈力值及勁度系數的定性分析。彈簧的勁度系數在實際測量時存在非線性，只有經多點測量才能準確判斷。受彈簧長度和壓力的制約，測量必須達到高精度要求。

自動測試裝置將實時采集的數據上傳給上位機監控程序，完成對彈簧勁度系數的非線性分析，為彈簧的后期分類提供理論依據。經用戶使用表明:該裝置檢測精度高、控制效果好，對地震檢波器性能的提升起到了很好的作用。

[1] 王化祥，張淑英.傳感器原理及應用[M].3版.天津:天津大學出版社，2007:77 －87.

[2] 周磊，陳時錦，程凱.超精密車床進給伺服系統的復合控制設計[J].機械設計與制造，2007(2):92－93.

[3] 李海波，張淑梅，林兆華，等.基于MSP430的步進電機調焦控制系統設計[J].儀表技術與傳感器，2011(1):98－100.

[4] 王亭嶺，熊軍華.3種脈沖計數檢測電路的設計與分析[J].華北水利水電學院學報，2010，31(4):76－79.

[5] 劉虹，何蘊增，楊麗紅.圓錐螺旋彈簧的非線性理論研究[J].哈爾濱工程大學學報，2005，26(5):628 －632.

[6] 刁紅泉，胡偉雄，顏鋼鋒.基于單片機的改進型五相混合式步進電機驅動器設計[J].工程設計學報，2004，11(1):19 －22.

[7] 張秦嶺，李艷明，郭宏.一種高性能兩相步進電動機細分驅動器的設計[J].北京航空航天大學學報，2006，32(9):1039 －1042.

[8] 阮太元，劉智勇.嵌入式系統在多功能精密高度測量儀中的應用[J].計算機測量與控制，2010，18(4):890 －891.

[9] 劉篤喜，楊朋偉，王宏旭.基于二次分步定位的快速精確位置控制方法研究[J].計算機測量與控制，2009，17(9):1724 －1725.

[10] 王艷春，羅少軒.基于MC9S08SH4和AD7705的智能傳感器系統設計[J].電子技術應用，2010(3):83－85.