雙歐控制法在運載器水彈道中的應用

王亞東, 袁緒龍, 張宇文

?

雙歐控制法在運載器水彈道中的應用

王亞東, 袁緒龍, 張宇文

(西北工業大學航海學院, 陜西西安, 710072)

潛射導彈運載器采用水平發射、垂直出水攻擊方式時, 常規的水彈道控制系統因歐拉姿態角奇異等問題難以正常工作。采用正反歐拉角2套姿態描述系統, 利用各自的奇異特點, 設計了在彈道初始階段利用正歐拉角控制規避和爬升彈道、末期利用反歐拉角精確控制出水俯仰角至90°的雙歐拉控制法, 并進行了仿真試驗。仿真結果表明, 利用雙歐拉控制法既可以保證彈道數據的直觀性, 又可大幅提高運載器出水俯仰角的控制精度。該方法不但可以用于運載器水彈道控制方案設計, 亦可用于同類別的涉及大姿態機動的控制系統設計。

導彈運載器; 水彈道; 雙歐拉控制法; 控制系統

0 引言

潛射導彈具有攻擊突然性、隱蔽性等突出的優點, 是各大國研究的熱點, 同時因其所處環境的特殊性, 導致了較復雜的力學、結構及彈道控制問題, 又是研究的難點。在短時期內, 新研發的潛射導彈等武器需要適應在役潛艇現有的發射裝置(魚雷發射管), 通過合理的匹配, 設計出導彈運載器。這樣既適應了原有發射裝置, 又巧妙地解決了彈體水密、彈道控制等問題。由于魚雷管為水平布置, 故導彈運載器為水平發射, 早期的運載器均采用斜出水方式, 攻擊扇面較小, 而運載器發展的趨勢則是優勢較大的垂直出水方式。

和常規武器不同的是, 水平發射、垂直出水彈道涉及俯仰通道從0°至90°附近的大幅機動, 同時, 為了保證發射艇的安全, 運載器爬升過程中還需做規避機動以偏離發射艇的主航道。常規的正歐拉角系統在俯仰角為±90°時為奇異點, 且根據歐拉角的定義, 俯仰角僅能在[–90°, 90°]區間內取值, 故當實際過程中出現跨越90°范圍時, 因定義區間的約束, 俯仰角仍會被限定在[–90°, 90°]內, 而其余通道數值則發生突變。各歐拉角是控制系統的重要參數, 控制指令多由其本身和目標值的偏差給出, 故突變對控制系統而言是災難性的, 會直接導致控制系統發散。

若不以姿態角作為控制的輸入參數, 僅解算無控彈道, 則采用反歐拉角作為姿態描述系統, 即可解決姿態奇異問題; 亦可采用四元數描述姿態, 均能滿足要求。但對于以姿態角作為控制參數的有控彈道而言, 四元數系統物理意義不顯著, 難以直接應用; 反歐拉角的控制律設計亦因角度描述不直觀而相當復雜。

本文設計了潛射導彈運載器水彈道的雙歐控制方案, 彈道解算中同時輸出正、反歐拉角2套參數, 根據彈道的不同階段采用不同的姿態角作為控制參數, 相應地給出了各自的控制律。將該方法應用到了某型運載器水彈道控制中, 完成了規避、爬升及出水角度精確控制等過程, 解決了常規控制方案存在的問題, 輸出參數直觀, 控制精度高。

1 運載器方案彈道

為了說明雙歐拉控制方法在運載器水彈道控制中的必要性, 首先給出水平發射、垂直出水運載器的方案水彈道。

潛射導彈運載器列裝于潛艇魚雷發射管, 依靠發射裝置的動力發射離管, 一般為了保證發射艇的安全性, 在運載器離艇一段距離后運載器發動機才點火, 控制系統啟控; 啟控后首先判斷發射深度是否滿足要求(限于運載器機動性特性, 深度太淺時不能完成水平至垂直的機動過程), 不滿足要求時首先操舵下潛至標準深度; 與此同時, 操舵完成規避發射艇主航向的機動; 而后操水平舵進行爬升和水平轉垂直姿態控制, 直至運載器出水。

運載器方案水彈道流程如圖1所示。

2 雙歐控制法

2.1 正、反歐拉角定義

如圖2所示建立固連于大地的地面坐標系, 原點置于水面上某一指定位置, 如發射時刻運載器浮心在水面上的投影點,坐標平面與水面重合,軸垂直向上。再建立原點位于浮心所在運載器橫截面幾何中心的體軸系,軸指向運載器頭部,軸在水平尾翼所在的平面內,軸與軸、軸組成右手坐標系。將地面坐標系原點平移至運載器浮心位置得到平移坐標系′′′。

運載器在空間的位置由運載器浮心在地面坐標系內的坐標給出。直觀起見, 運載器在空間的姿態仍由歐拉角系統中的3個歐拉角表示。常規的正歐拉角系統定義為: 體坐標系從與平移坐標系重合的位置開始依次繞對應的,,向相關軸旋轉這3個角度得到的姿態用3個歐拉角組合來表示, 分別稱為偏航角、俯仰角和橫滾角。

在正歐拉角定義下, 由地面系到體坐標系的轉換矩陣

歐拉方程

(2)

對于一般航行器而言, 俯仰方向機動不會超過90°, 采用正歐拉角表示已經足夠。然而對于本文研究的運載器而言, 其方案彈道為水平發射, 垂直出水, 俯仰角度會增大至90°甚至更多, 若仍采用正歐拉角描述, 在俯仰角超過90°時, 偏航角和滾動角均會發生突變, 表示不直觀且不利于彈道控制系統設計。

本文采用了雙歐法(正、反歐拉表示)來描述彈體姿態或作為控制參數使用, 在此一并給出反歐拉角描述的推導方式和正反歐拉角轉換關系。

反歐拉角轉動順序依次為

對應的坐標轉換矩陣為

(3)

反歐拉角對應歐拉方程為

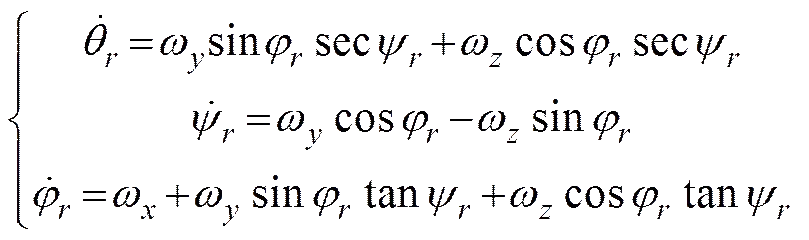
不論采用何種歐拉角, 其定義的姿態是一致的, 因此地面系到彈體系的轉換矩陣應相等, 依此來推導正反歐拉角轉換關系。式(5)給出了推導得到的正歐拉角轉為反歐拉角的轉換關系(代表轉換矩陣中對應行列的數值)。

(5)

相反的變換亦可通過相同的方法推導而得。

2.2 問題提出

運載器為水平發射, 垂直出水, 為了提高控制精度, 需要將俯仰角控制目標定為90°, 但這會給控制系統的設計帶來很大的麻煩。

首先, 正歐拉角系統描述彈體姿態時解算出來的各個角度是有范圍的, 即, 因此當俯仰角趨近于90°時, 若繼續偏轉, 實際上會出現大于90°的情形, 但在正歐拉角系統解算下, 其會被限制在[–90°,90°]區間, 而其余2個角度會產生突變, 這種不連續會造成控制系統發散。

若采用2.1節中所述的反歐拉角來定義彈體姿態則可以解決參數突變問題, 但由于其定義的不同, 導致這種角度應用于控制不直觀, 沒有正歐拉系統的意義明確。

為了解決此問題, 本文采用了雙歐方法進行彈道控制: 彈道解算時實時輸出2套歐拉角, 在方案彈道初期采用物理意義明確、直觀的正歐拉角系統進行控制; 在趨于出水時刻, 換用反歐拉角系統將姿態精確控制為垂直。如此以來, 獲得直觀的參數表示和精確的出水控制結果。

2.3 控制方案

以俯仰角為控制目標, 比例微分方式設置控制律, 下面將給出詳細的控制方案。

首先, 控制系統啟控時, 設置控制狀態為狀態1, 即采用正歐拉系統進行控制。

1) 當發射深度小于標準深度時, 先下潛同時偏航控制1 s, 然后開始爬升。

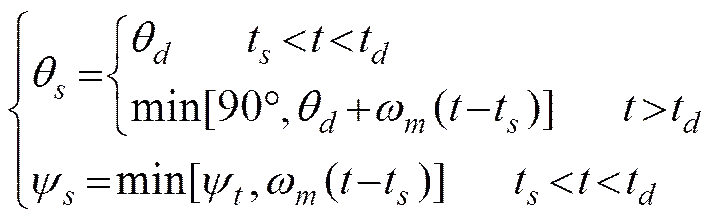
2) 當發射深度大于或等于標準深度時, 先偏航控制1 s, 然后開始爬升。

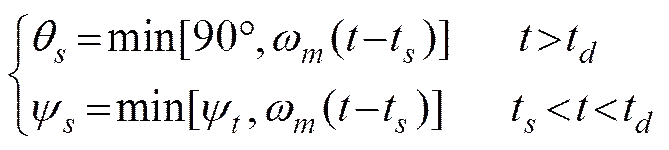
式中符號含義同上。

舵角指令按式(8)給出。

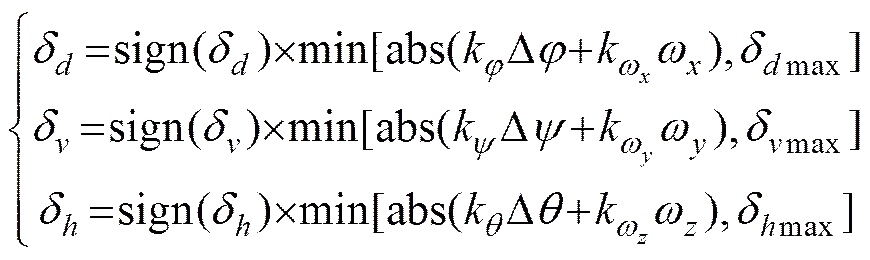
式中: 定義d, d, d分別為反歐拉系統下的俯仰、偏航和橫滾角控制指令;由反歐拉角系統下對應的歐拉方程給出, 并且

舵角指令的確定和式(8)不同, 需要進行分配, 如式(10)所示。

一般情況下, 此階段僅為精確控制, 舵角不會很大; 但若某通道需用舵角超過了最大舵角限制, 應注意按比例縮減所有的舵角。

3 仿真結果與分析

根據設計的控制方案, 考慮不同發射深度下的彈道, 在小于標準深度時先下潛至標準深度(深度差不會很大, 以最淺深度設置目標下潛角以滿足下潛深度要求), 大于標準深度時則彈道僅增加了標準深度彈道垂直爬升段的延伸, 故全彈道控制方案的檢驗可使用標準深度對應的標準彈道完成。采用上述雙歐拉法控制方法進行標準深度下潛射導彈運載器水下方案彈道仿真, 結果如圖3~圖7所示。

由圖3可以看出, 彈道前期, 采用正歐拉法進行常規意義下的規避彈道和爬升彈道控制, 得到了較好的控制結果, 且控制律較簡單, 彈道參數直觀; 在彈道末期, 即控制彈體以90°姿態出水階段, 改用反歐拉法控制, 在本文給出的切換準則85°俯仰角下, 彈道過渡平滑, 未出現控制參數突變, 且成功適應了俯仰角超調過90°的情形, 最終將俯仰角控制在90°附近。

采用雙歐拉法控制的優勢是顯而易見的, 對于一般的控制系統, 為保證控制的快速性, 控制過程中參數相對于目標均會有小幅超調, 若僅采用常規的正歐拉法控制, 為了防止出現超過90°的突變, 目標參數僅能設置為小于90°的數值, 原理上偏離了垂直出水的要求, 準確性不夠。而雙歐拉繼承了正歐拉控制律簡單、參數直觀的優點, 兼顧了終態穩定性要求, 消除了參數突變弊端, 很好地解決了水平發射、垂直出水彈道控制的技術難點。

4 結論

根據水平發射、垂直出水導彈運載器水彈道的特點和存在的問題, 設計了雙歐拉控制法, 該方法在彈道前期規避、下潛、爬升等機動控制時采用直觀的正歐拉法控制, 在可能出現參數突變的彈道末期采用反歐拉法控制, 得出以下結論。

1) 選擇合理的控制參數, 雙歐拉法可適應各發射深度下運載器水彈道控制;

2) 雙歐拉法從原理上采用了更準確的控制目標, 可保證運載器出水姿態控制在90°附近, 且不存在控制參數的突變;

3) 雙歐拉法同時輸出了2套姿態參數, 既保證了姿態判讀的直觀性, 又滿足了控制的需求。

[1] 王亞東, 袁緒龍, 覃東升. 導彈水下發射筒口氣泡特性研究[J]. 兵工學報, 2011, 32(8):991-995.Wang Ya-dong, Yuan Xu-long, Qin Dong-sheng. Research on the Outlet Cavity Feature during the Launch of Submarine Launched Missile[J]. Acta Armamentarii, 2011, 32(8): 991- 995.

[2] 馬溢清, 李欣. 潛射導彈水下垂直發射方式綜述[J]. 戰術導彈技術, 2010, 31(3): 124-128. Ma Yi-qing, Li Xin. Review on Underwater Vertical- launching Mode for Submarine-launched Missiles[J]. Tactical Missile Technology, 2010, 31(3): 124-128.

[3] 葛暉. 潛射導彈發射安全性研究[D]. 西安: 西北工業大學, 2004.

[4] 袁緒龍, 張宇文. 運載器垂直出水彈道姿態角奇異性問題研究[J]. 彈箭與制導學報, 2005, 25(2):83-87.Yuan Xu-long, Zhang Yu-wen. On Singularity Problem of Water-exit Trajectory of the Missile Carrier[J]. Journal of Projectiles, Rocket s Missiles and Guidance, 2005, 25(2): 83-87.

[5] 許毛躍, 張登成, 李嘉林. 四元數在歐拉方程中的應用研究[J]. 飛行力學, 2002, 20(1): 67-70.Xu Mao-yue, Zhang Deng-cheng, Li Jia-lin. Study of the Application of Quaternions to Euler Equation[J]. Flight Dyna- mics, 2002, 20(1): 67-70.

[6] 張宇文. 魚雷彈道與彈道設計[M]. 陜西: 西北工業大學出版社, 1998.

(責任編輯: 陳 曦)

Application of Dual-Euler Control Method to Water-Trajectory Design of Missile Carrier

WANG Ya-dong, YUAN Xu-long, ZHANG Yu-wen

(College of Marine, Northwestern Polytechnical University, Xi′an 710072, China)

When a sub-launching missile carrier takes horizontal launch and vertical water-exit, the traditional water trajectory control system fails to work normally due to the singularity of Euler angles. In this paper, two Euler angle systems with their own singularity features are adopted to design a new control method. In initial stage of trajectory, positive Euler angles are used to accomplish the evadable and ascending motions, while the reverse Euler angles are employed to control pitching angle to 90°precisely at the water-exit stage. Simulation results show that the proposed dual-Euler control method can make the trajectory data intuitive and clearly improve the precision of water-exit pitch angle. This method can be applied to control scheme design of missile carrier water trajectory, and can also be extended to related control system design concerning large attitude maneuver.

missile carrier; water trajectory; dual-Euler control method; control system

TJ630.1; TJ762.4

A

1673-1948(2013)06-0401-05

2013-03-03;

2013-05-20.

王亞東(1985-), 男, 在讀博士, 主要研究方向為水中兵器發射和總體研究.