一種用于自適應跳頻系統的新型交織方法

盧繼華，黃承飛，李祥明

(北京理工大學 信息與電子學院，100081 北京)

跳頻技術在民用通信中常用于多用戶共享頻帶解決頻譜擁擠，且廣泛應用于各種現代通信系統中.如自適應跳頻用于減輕802.11x 的WLAN(Wireless Local Area Network)系統干擾［1］;在帶有RAKE 接收機的TDMA/CDMA 中應用慢跳頻來提高系統在多徑瑞利衰落信道中的性能［2］;在藍牙系統中應用增強的自適應跳頻來抗定頻干擾和變頻干擾［3］.在WLAN 的信道綁定技術中使用信道交織技術可以提高誤比特率性能［4］.對于跳頻(Frequency Hopping，FH)通信系統而言，由于FH 系統本身就是1 個自干擾系統，系統中用戶間的干擾比較突出.因此，克服干擾的途徑之一是設計出盡可能低漢明互相關性的工程實用碼型，途徑之二是運用一些消除或減弱干擾的跳頻技術，如自適應跳頻技術，差分跳頻技術等［5］.自適應跳頻技術應用廣泛，跳頻系統在跳頻速率很高時對載頻的跳變精度及速率均要求很嚴格，因此設備復雜性相應增加［6］.基于交織的跳頻系統將突發錯誤在譯碼之前分散開來，將大范圍的突發錯誤轉為隨機錯誤，提高差錯控制編碼的糾錯、檢錯能力，繼而提高整個通信系統的性能，降低系統實現的復雜度，并且具有一定的抗干擾能力［7］.而不同的交織方法對整個系統的抗干擾性能的提升是不同的，傳統的行列交織雖然實施簡單，但是其抗干擾性能并不理想，交織后信息序列之間的相關性依然較大.

本文給出了一種用于自適應跳頻系統的新型交織方法，實現了利用素數碼族進行交織，滿足降低了信息序列相關性的同時，交織延時和存儲量的需求也大大降低，降低了高速跳頻系統實現時對系統復雜度的需求.分析及仿真結果表明，本文提出的新型交織方法具有優良的抗干擾性能.

1 基于素數碼交織的跳頻系統

無線通信系統中，用自適應跳頻系統來克服人為干擾已有較為廣泛的應用［8］，這些系統常采用多進制調制與非相干解調.圖1 為本文在基于素數碼交織的自適應跳頻系統框圖［9］，其中虛線框內為本文提出的新型交織方法，包括交織與解交織環節.

圖1 自適應跳頻通信系統框圖

從圖1 可以看出，基于素數碼交織的自適應跳頻系統信號流程如下:隨機產生的數據為信源，信源經RS 信道編碼后交織，再依次進行MSK 調制、CIC 濾波，經中頻載波頻移和跳頻調制后發送到信道.在信道中依次加入噪聲和干擾.系統接收端的處理流程與發送過程相反:接收端先對接收到的信號進行解跳，而后依次進行中頻解調、CIC 抽取濾波、MSK 解調后進行解交織，再經RS 解碼得到發端信息.在接收端得到信息后要計算當前頻點的誤碼率，并根據誤碼率自適應選擇跳頻頻點.

設經過MSK 調制的基帶信號為S(t)，信道中加入的高斯白噪聲為N.則加入噪聲后的信號為

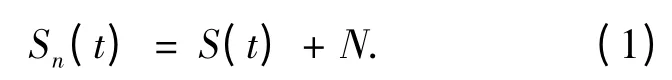
中頻標稱頻率為fc，干擾功率系數為J，干擾的頻率偏移為Δf，則加入干擾后的信號為

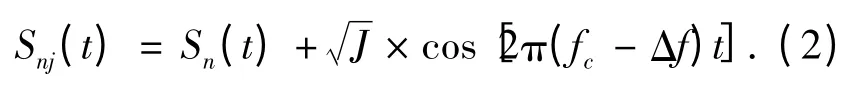
2 交織方法概述

2.1 問題描述

交織器一般可分為隨機和確定性交織器兩大類，是以一一映射的方式將輸入符號的順序重置，而解交織器將被交織器置亂的符號重新排成原始順序.各種交織技術及多重交織技術已被民用及軍用系統的各種標準廣泛采納和應用，其中最典型的是基于Turbo 信道編碼的系統和WLAN 標準中［4，7，10］.如:并行Turbo 譯碼器結構結合交織技術應用于高速率系統中［11］;WLAN系統的IEEE802.11n 協議中的交織器硬件結構［12］;3GPP標準中的Turbo 交織是將輸入比特流在矩陣中進行行內和行間交織得到新矩陣，再剪切后得到輸出比特流;另有研究表明基于整數環模置換多項式的交織器性能比較好，二次置換多項式交織器實現最大擴展因子可進一步提高Turbo 交織的性能［13－14］.

衡量交織器性能的典型參數除不動點數目外，還有交織相關系數、交織延時、存儲量.下面對各衡量參數進行簡單說明.

1)交織相關系數.交織相關系數是用來衡量交織器性能的好壞.在交織矩陣的大小為M×N下，交織相關系數為

顯然，相關系數ρ 越小越好.

(2)交織延時.交織延時是指任何1 個符號在它被插入到輸出序列之前所經過的最大延遲時間.

(3)存儲容量.存儲容量是指交織器或解交織器交織矩陣的大小.一般來說交織陣的存儲容量越大，相應的交織延時也越長，通信的實時性越差，但交織的效果也越好.因此需對通信實時性和交織效果進行折中.

2.2 行列交織方法

行列式的分組交織也稱為塊交織，分組長度為L=M×N，故又稱之為(M，N)分組交織.行列交織的地址序列是按列寫入按行讀出，如圖2 所示.行列交織分為A 型和B 型，兩者寫入方式相同，A 型讀出順序是從前往后按列讀出，B 型是從后往前按列讀出.

2.3 偽隨機交織方法

偽隨機交織方法的交織規則如下:對于長度為n 的信息序列，先標記每個比特位置，再生成相應n 個［0，1］之間的隨機數，按產生的順序排列成序列X，每個隨機數對應于信息序列中相應位置的信息比特，再把X 中元素按一定規則重新排列得到新序列Y，并按Y 中元素的順序讀出相應的信息比特.Y 中元素的位置順序便是偽隨機交織的地址序列.對偽隨機交織而言，每個長度為N的偽隨機交織器共有N 種交織方式，體現了香農在有噪信道編碼理論中的“隨機特性”.

圖2 行列交織方法的實現示意

從性能角度，在眾多交織方法中，偽隨交織方法性能最優.但偽隨交織方法也有如下缺點:

1)在短幀交織下，采用偽隨機交織器計算產生的隨機數間存在一定相關性;

2)對每一組(幀)信息序列所用的交織器均不相同，具有一定隨機性，而譯碼器要求對每幀數據有相應的解交織器對其解交織，所以在傳輸編碼序列時，信道上還需傳輸交織器信息，加大了信道傳輸負載.若交織器信息出現錯誤，會使譯碼的誤碼增多.在最先提出的Turbo 碼中C.Berrou 等使用的就是偽隨機交織器.通過增加隨機性，將混沌交織器和Dithered Relative Prime(DRP)交織器相結合，Turbo 碼的誤比特性能會有所提升［15］.

3 新型交織方法

在跳頻通信系統中，采用交織的方法將Turbo編碼符號均勻的分散在各個數據跳內，從而達到使單跳信息被刪除的影響降低到最小的目的.本文提出的新型交織方法利用素數碼及平方素數碼的特性，產生素數碼族作為交織的地址序列.與其他常用交織方法相比，具有實現簡單、低延時以及占用存儲資源少的特點.采用本文交織方法與不采用交織相比，在系統復雜度小幅增加前提下，顯著提高了自適應跳頻通信系統的抗干擾效果.

3.1 新型交織方法概述

本新型交織方法根據交織符號的個數選擇合適的素數p 產生素數碼矩陣，從而形成地址序列.信號序列先要變成信號矩陣并根據產生的素數碼矩陣調整信號矩陣，而后依照素數碼矩陣對信號矩陣進行交織.接收端的解交織過程與交織相反.接收到的信號先變換為矩陣，再依據與發端相同的素數碼矩陣進行解交織，而后根據素數碼矩陣對解交織后的矩陣進行調整，變換為序列后便可進行信道解碼.

3.2 素數碼及平方素數碼的產生

新型交織方法的地址序列基于素數序列族.素數序列族起源于E.L.Titlebaum 提出的線性同余跳頻碼(Linear Congruence Code 碼)［16］.

1)素數碼的產生.素數碼構造方法是利用模p 乘法表(p 為素數).設p 為素數，由su(j)=uj mod p 定義的長度為L=p 的序列

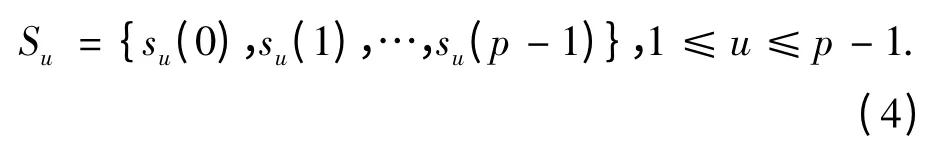
將素數碼為有限基域乘法結果的構造思想進一步延伸到有限擴域GF(p2)上，即研究基于有限域GF(p2)以形為x2－y－1(y 為素數p 的二次非剩余)的二次既約多項式為模的域乘法結果，構造出新的跳頻序列族，因其序列長度為p2，因此命名為平方素數碼.

2)平方素數碼的產生.有限擴域GF(p2)乘法是由以GF(p)中元素為系數的n－1 次多項式以n 次既約多項式f(x)為模實現的［17］.平方素數碼只考慮n=2 情況.由有限域理論，可以證明二次多項式f(x)=x2－y 為GF(p)上的二次既約多項式，其中，y 為素數p 的二次非剩余.

為實現素數碼在GF(p2)上的擴展，以GF(p)中元素的二維向量來表示上述素數碼中的各個參數，設(i，j)表示橫軸序號l，(a，b)表示碼字序號m，(k1，k0)表示縱軸序號k，這里l=ip+j，m=ap+b，k=k1p+k0.對應的多項式分別為:l(x)=ix +j，m(x)=ax +b，k(x)=k1x +k0，i，j，a，b，k1，k0∈GF(p)且(a，b)≠(0，0).根據以上約定，以f(x)=x2－y 為既約多項式，由下式實現GF(p2)域乘法:

其中:⊕表示模p 加，i，j，a，b ∈GF(p)，且(a，b)≠(0，0).(a，b)，(i，j)分別表示碼字序號及時隙序號，對應序列表示為(aj ⊕bi，bj ⊕yai).

3.3 新型交織方法中地址序列的產生

控制自適應跳頻系統信息符號交織的地址序列選擇素數碼，其具體實現規則為:有限域GF(p)上模p(p 為素數)乘法的生成表達式如下:

其中:k 表示縱軸序號;m 表示碼字序號;l 表示橫軸序號［18］.

素數碼矩陣的具體構造過程如下:

1)設p 為素數;

2)將有限域GF(p)上的元素以升階或降階列出，如:G={0，1，2，…，p－1}.

3)將G 中各元素同乘某一非零域元素u，1 ≤u ≤p－1，得到1 個非重復序列Su，

4)通過乘以不同的非零域元，共可得到p－1 個長度為p 的非重復序列.以p=13 為例，按上式構造素數碼，得到如表1 所示的素數碼矩陣.

表1 p=13 時的素數碼矩陣

新型交織方法的交織地址序列采用素數碼矩陣中的非零值和非自然排序序列，即上表1 中的粗體數字，作為新型交織方法中的地址序列.

3.4 新型交織方法的實現

信號序列要變換成M×N 的矩陣，而后根據信號序列的矩陣大小產生維度合適的素數碼矩陣，依照修正后的素數碼族矩陣對信號序列進行交織，通常為了節省空間可以在形成矩陣某行后進行交織，交織形式可為行或列交織.素數碼交織后的信號矩陣再變為信號序列就完成了交織;接收端在接收到信號序列后先要將信號序列變換成與發送端相同維度的M×N 矩陣，而后用與發送端嚴格同步的素數碼矩陣對此信號矩陣進行解交織，解交織后的信號矩陣變換為信號序列后就可進行后續處理，如圖3 所示.

本文提出的交織方法與行、列交織相比實現簡單而靈活.在交織過程中根據每組信息符號個數確定素數p 的值，只要保證素數碼矩陣的元素大于信息符號的個數即可.

圖3 新型交織方法的系統流程

4 各種交織方法性能比較與仿真分析

基于上述新型交織方法的描述，用matlab 軟件搭建的“基于交織的自適應跳頻系統”對其進行Monte Carlo 仿真，并與其他交織方法進行性能比較.仿真的系統參數如下:對基帶信號進行MSK 調制，基帶信息速率為50 kbps，基帶信號帶寬為60 kHz;信道噪聲為高斯白噪聲;單音干擾相對于中頻的偏移為400 kHz，干擾的功率系數為0.011;跳頻速率為5 kbps;中頻載波頻率范圍為從600 kHz 到3 750 kHz，相鄰載波頻率間隔為50 kHz;備選頻率范圍為從3 800 kHz 到5 350 kHz，相鄰備選載波頻率間隔也為50 kHz;共有64 個載波頻點及32 個備用載波頻點供隨機選擇;SNR 的范圍為5～30 dB;并假設接收端在跳頻圖案獲得理想同步情況下后進行解交織.仿真結果如圖4 所示.

圖4 新型交織方法與其他交織方法的性能比較

圖4 中的誤碼率數值都是經過30 次，每次106個仿真數據進行仿真并平均得到的，這里仿真數據量的選取原則按照Eb/N0為30 dB，結合置信度為99% 誤碼率的公式計算得出，即仿真數據總量≥100/Pe，等于106.從圖4可見，在Eb/N0小于15 dB 時，各種交織方法的誤比特率性能十分接近;在Eb/N0從15 dB 到30 dB 變化時，無交織時的誤碼率曲線下降趨勢相對比較緩慢，性能最差;行列交織的誤碼率曲線較平滑下降，性能稍好;素數碼和平方素數碼交織的誤碼率性能均好于行列交織，兩條曲線有交疊，表明二者性能相當;偽隨機交織性能最好，但隨SNR 增大，曲線下降速度并沒有素數碼和平方素數碼誤碼率曲線下降的快，這表明素數碼族交織在信噪比較高時，性能逼近偽隨機交織.由此可看出本文提出的交織方法對單音干擾有較好的抑制效果，其抑制干擾的性能要好于普通的行列交織方法，而與偽隨機交織方法的性能相差不多.進一步的，基于交織方法4 個主要性能參數，對本仿真平臺使用各種交織方法進行性能評估.仿真過程中，對于不同交織方法均采用輸入相同點數的數據進行交織.對于行列交織和偽隨機交織，它們存儲的是整個交織表，且在行列交織中按行輸入按列讀出第1 個點和最后1 個點的位置保持不變.經過對各種交織方法的交織參數的仿真與計算，得出各種交織器的性能參數如表2 所示.

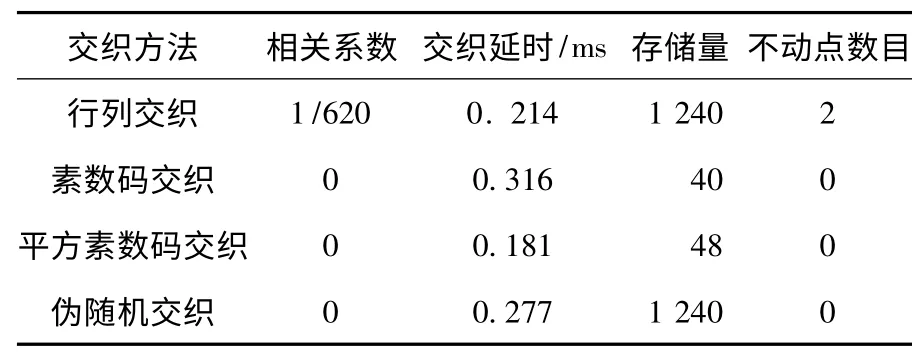
表2 幾種交織方法性能參數的比較

由表2 可以看出素數碼族交織在各方面都要優于行列交織，尤其在存儲量上要明顯好于行列交織.而本文提出的新型交織方法和偽隨機交織相比，在交織延時和存儲量上也占有一定的優勢，在存儲量上的優勢尤為明顯.素數碼交織的存儲量優勢，體現在數據以行或列進行交織，地址序列每計算出一行地址值就可進行這一行的交織，不需要多余存儲其他行的數據，因此存儲量大大降低到每行元素的個數(本仿真中行元素為40).

綜合表2 可以看出素數碼交織和平方素數碼交織在相關系數、交織延時和存儲量上和常規的行列交織和偽隨機交織相比有較大優勢.

5 結論

本文給出的新型交織方法使用素數碼族生成交織地址序列，具有相關系數小、低延時、存儲量需求小且實現靈活，不用刻意考慮矩陣維數的特點.能夠改善系統出現連串錯誤時超出糾錯編碼糾錯能力的抗誤碼性能.仿真結果表明新型交織方法使自適應跳頻系統對單音干擾有較好的抑制效果，其抑制干擾的性能與平方素數碼相當，好于普通的行列交織方法，而僅僅略低于隨機交織的性能.因此，新型交織方法使得自適應跳頻通信系統具有較好的抗干擾性能，具有廣泛的應用前景.

［1］LEE S H，LEE Y H.Adaptive frequency hopping for bluetooth robust to WLAN interference［J］.IEEE Communications Letters，2009，9(13):628－630.

［2］CORREIA A M C，RODRIGUES A C B.Adaptive frequency-hopping for TDMA/CDMA［C］//48thIEEE Vehicular Technology Conference.Piscataway:IEEE.1998，3:2212－2216.

［3］HSU A C，WEI D S L，JAY KUO C C.Enhanced adaptive frequency hopping for wireless personal area networks in a coexistence environment［C］//IEEE Conference on Global Telecommunications.Piscataway:IEEE.2007:668－672.

［4］KABASHI A H，O＇FARRELL T.Low complexity CMCCDM based wireless LAN with different interleaving approaches［C］//IEEE 19th International Symposium on Personal，Indoor and Mobile Radio Communications.Piscataway:IEEE.2008:1－5.

［5］黃建平.基于周期無碰撞區跳頻序列的自適應跳頻系統研究［D］.成都:西南交通大學，2009.

［6］DING C S，YIN J X.Sets of optimal frequency-hopping sequences［J］.IEEE Transactions on Information Theory，2008，8(54):3741－3745.

［7］SIAUD I，ULMER-OLL A M.Advanced dynamic binary interleaving codes for UWB-OFDM WPAN systems［C］//IEEE Conference on GLOBECOM Workshops.Piscataway:IEEE，2009:1－6.

［8］ANDERSSON G.LPI performance of an adaptive frequency-hopping system in an HF interference environment［C］//IEEE 4th International Symposium on Spread Spectrum Techniques and Applications.Piscataway:IEEE，1996，2:903－907.

［9］Liu Y S.Bit-interleaving in fast FH/SSMA systems with M-FSK modulation［J］.IEEE Transactions on Wireless Communications，2007，6(9):3154－3158.

［10］JASPAR X，VANDENDORPE L.Impact of variable length codes on the interleaving gain of turbo systems:the concept of bounded spectrum.IEEE Transactions on Communications，2011，59(7):1796－1806.

［11］TARABLE A，BENEDETTO S.Mapping interleaving laws to parallel turbo decoder architectures［J］.IEEE Communications Letters，2004，8(3):162－164.

［12］張振東，吳斌，朱勇旭，等.IEEE802.11n 無線局域網中的多模交織研究與實現［J］.電子科技大學學報，2011，40(3):383－387.

［13］SUN J，TAKESHITA O Y.Interleavers for turbo codes using permutation polynomials over integer rings［J］.IEEE Transactions on Information theory，2005，51(1):101－119.

［14］TAKESHITA O Y.A new metric for permutation polynomial interleavers［C］//ISIT.Seattle:［s.n.］，2006:1983－1987.

［15］張衛黨，康惠平，高輝.Turbo 碼中一種基于混沌映射的DRP 交織器設計［J］.鄭州大學學報(工學版)，2011，32(5):73－76.

［16］TITLEBAUM E L.Time-frequency hop signals—part I:coding based upon the theory of linear congruences［J］.IEEE Trans，1981，AES-17(4):490－493.

［17］LIDL R，NIEDERREITER H.Finite fields ［M］.London:Addision-Wesley Publishing Company，1983.

［18］梅文華.跳頻通信［M］.北京:國防工業出版社，2005.