基于四邊形網格參數細分的平面與自由曲面求交算法*

李慧瑩，陳良驥

（鄭州航空工業管理學院 機電工程學院，河南 鄭州 450015）

0 引 言

一直以來，平面與曲面間求解交線的問題都是計算機輔助設計與制造（computer-aided design/manufac?turing，CAD/CAM）編程領域中最普遍的工程問題。在曲面造型與裁剪、加工刀具軌跡計算、加工幾何圖形驗證等實際應用中，常常需要對平面與曲面進行求交運算［1-3］。國內外在求交計算方面做了大量的研究，大致包括牛頓迭代法［4］、曲面離散法［5-6］、區間算術法［7］、光線跟蹤法［8-9］以及近年來出現的等值線法［10］、三角網格方法［11-12］等。牛頓迭代法通常是在給定初值后將求交問題轉化為求線性方程組或常微分方程解的問題，但收斂與否以及收斂的速度與迭代初值的選取有很大關系。曲面離散算法是用小平面片近似逼近曲面的一種幾何求交算法，有較高的可靠性，但缺點是運算量較大、效率低、精度低。區間算術法的提出則只是為了解決直線與隱曲面求交的問題。

鑒于以上各種求交算法各自的缺點，本研究將首先提出一種四邊形參數曲面片模型，在此基礎上可將平面與自由曲面的求交問題簡化為直線段與平面的位置關系問題。與現行常見的求交方法相比，本研究算法的特點是計算穩定可靠、精度高而且具有較強的普適性。

1 自由曲面的NURBS表示

一張笛卡爾空間自由曲面可表示為如下非均勻有理B樣條形式［13-14］:

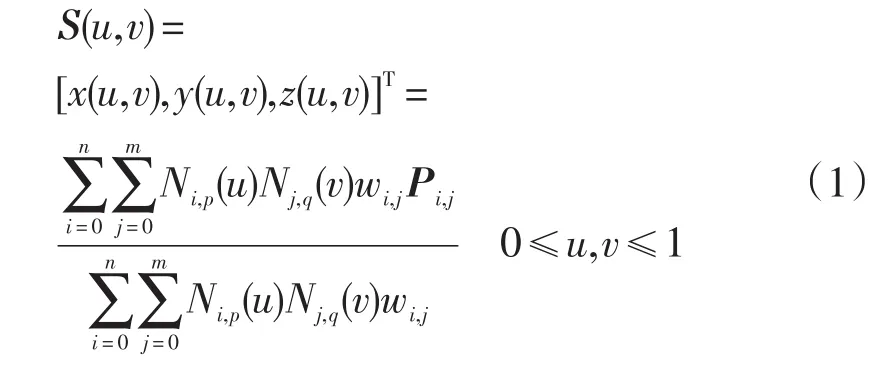
式中:Pi,j—三維控制點；wi,j—Pi,j對應權重；（n+1）,（m+1）—u向和v向控制點的數目；Ni,p(u)，Nj,q(v)—沿u向的p次和v向的q次B樣條基函數。

由自由曲面的NURBS定義可知，一張自由曲面對應于參數平面內一正方形區域｛（u,v）|0≤u≤1，0≤v≤1｝，笛卡爾空間與參數空間的映射關系如圖1所示。

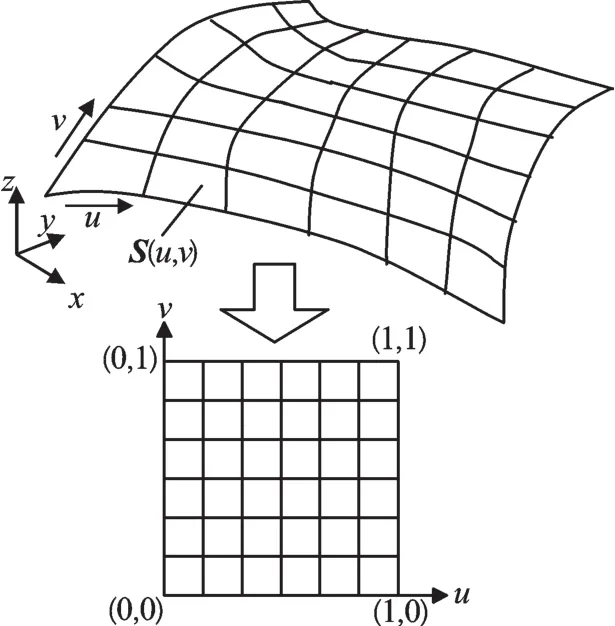
圖1 笛卡爾空間與參數空間的映射關系

2 空間點、線與平面的關系

2.1 空間點V與平面的關系

已知平面單位法矢為｛A，B，C｝、平面常數為D，平面與曲面相交如圖2所示。平面為所有點V=（x，y，z）的集合｛V|F（V）=F（x，y，z）=Ax+By+Cz+D=0｝。該平面將空間分為3個部分，即｛V|F（V）＜0｝、｛V|F（V）=0｝和｛V|F（V）＞0｝。因此，空間任一點V與平面有如下關系:若點V在平面上，則F（V）=0；反之，若V使得F（V）≠0，則V定不在平面上。

圖2 平面與曲面相交

2.2 空間線段V1V2與平面的關系

空間線段V1V2與平面的關系可由線段兩個端點V1和V2分別與平面的關系來確定。具體位置關系可以有以下4種情形:①若V1和V2分布在平面相同一側，則線段V1V2與平面不相交，此時F(V1)、F(V2)皆非零且具有相同的符號；②若V1和V2分布在平面相異一側，則線段V1V2與平面交于一點，此時F(V1)、F(V2)皆非零且具有相異的符號；③若V1（或V2）在平面上而V2（或V1）不在平面上，則線段與平面交于V1（或V2）；④若V1和V2都在平面上，則線段位于平面上。

將以上線段與平面之間的關系歸納如下:

3 四邊形參數面片

如圖1所示，位于笛卡爾空間的曲面的每個空間四邊形都對應于參數平面內的一個小長方形。四邊形參數面片模型如圖3所示，本研究將每個長方形分別按照一定順序標記出4個角點（1、2、3、4）和4條邊（Ⅰ、Ⅱ、Ⅲ、Ⅳ），并定義這樣的長方形為四邊形參數面片。參數平面內，平面與曲面交線的參數變化曲線v=f(u)，如圖4所示。本研究用前一小節中介紹的兩種關系可以判定出各個空間四邊形每個邊與平面的關系，進而可以判斷出四邊形參數面片與v=f(u)的位置關系。曲面所有四邊形參數面片與v=f(u)間的位置關系分別會有如圖3所示的a、b、c、d、e、f、g等7種狀態。

圖3 四邊形參數面片模型

本研究對這7種狀態分別做如下定義:①空間四邊形的每個邊均在平面的相同一側為a態；②空間四邊形的僅有一個頂點在平面上為b態；③空間四邊形的兩個相鄰邊與平面相交為c態；④空間四邊形的一個頂點在平面上、一條邊與平面相交為d態；⑤空間四邊形的兩個對邊與平面相交為e態；⑥空間四邊形的兩個對角頂點在平面上為f態；⑦空間四邊形的某邊位于平面上時為g態。

4 交線鏈表生成

對圖1中的每個小四邊形，順次計算各角點坐標，應用前面所介紹的兩種關系和幾種狀態的定義方法，可以得到如圖4所示的一張狀態表。

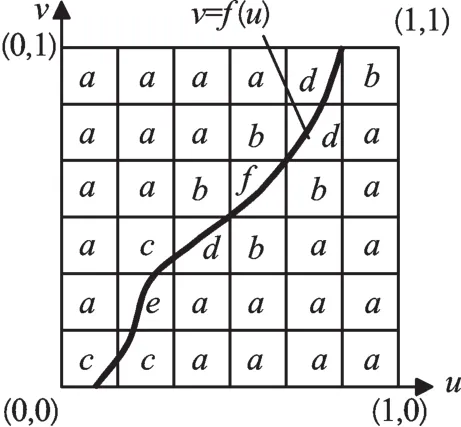
圖4 參數變化曲線與狀態表

求交線的過程為:①建立一張空的四邊形面片結構的鏈表并對照狀態表將所有處于非a態和非b態的四邊形按一定順序（如從下到上順次取出每一行、對取出的每行按從左至右順次取出每個四邊形）存入該鏈表中，得到一張初始鏈表；②對初始鏈表中所有處于非f態以及非g態的各結點（小四邊形）按同樣的方法再進行細分，并將細分后得到的所有非a態和非b態的四邊形按與前面相同的順序插入該鏈表中，得到一張新鏈表；③重復第②步的操作直到鏈表中所有的結點狀態都為f態和g態為止。最后得到的四邊形鏈表能很好地逼近交線且交線必然位于平面內，稱該鏈表為交線鏈表。以圖4表示的狀態表來說明該計算過程，求交線鏈表的過程如圖5所示。

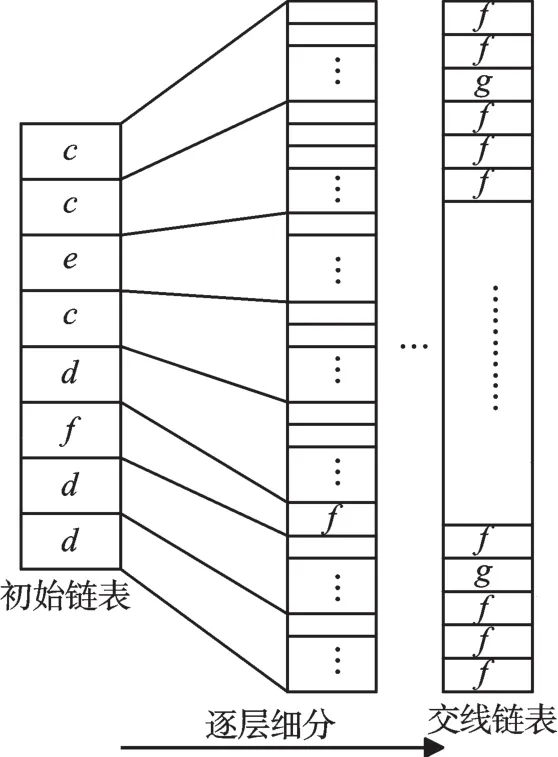
圖5 求交線鏈表的過程

將交線鏈表中各四邊形位于平面內的角點作為型值點，用NURBS樣條進行擬合，即可得到平面與自由曲面的交線。

5 實例計算

本節將以一張雙三次NURBS曲面為例對所提出的方法進行驗證。該曲面由16個控制點形成，各控制點權重取為1。為說明問題，先找出曲面上已知的3個點P、P1和P2，通過這三點確定一個平面，求這個平面與自由曲面的交線。

取P=S(0.5,0.5)=[30,67.5,45]T，P1=S(0.15,0.35)=[9,34.528 3,31.5]T，P2=S(0.85,0.65)=[51,34.321 7,58.5]T，經計算，由點P、P1和P2所確定的平面方程各系數分別為:A＝0.540 757 6，B＝0.0，C＝-0.841 178 5，D＝21.630 304。利用VC++和OpenGL在計算機上編程實現了本研究所提出的求交算法，從初始鏈表開始，對鏈表中每個四邊形分別進行10×10細分，共經過6層細分可以得到圖5中的交線鏈表，對其進行曲線擬合，求得的平面與自由曲面的交線如圖6所示。

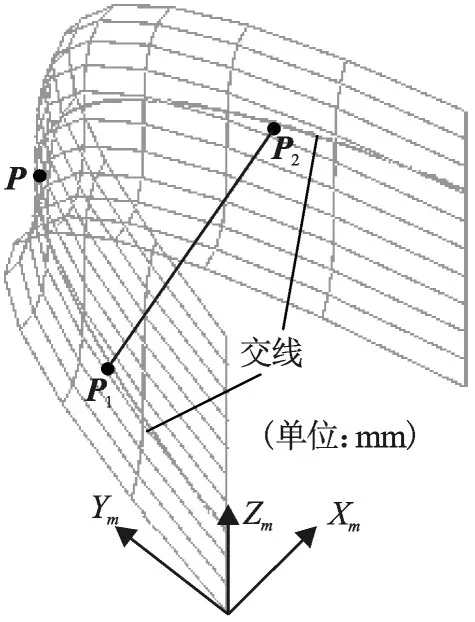
圖6 平面與自由曲面的交線

以下通過求直線與交線的交點來進一步驗證算法的精確性。理論上，P1、P2應該在交線上，但實際計算平面內直線P1P2與交線的交點時采用將曲線變折線段的方式進行，因而只能得到它們的近似值和，求得的和分別為:

與P1和P2的距離誤差分別為:

6 結束語

本研究所提出的平面與自由曲面求交線方法的思路是:根據笛卡爾空間與參數平面之間的映射關系，將空間四邊形與平面的位置關系轉化為參數平面內四邊形與交線參數變化曲線間的關系，進而求得交線。最后，本研究結合實例進行了計算，研究結果表明，求得的交線能夠與理論交線精確符合，完全可以在幾何造型、曲面裁剪以及五軸編程刀位計算等諸多方面得到實際應用。

（References）:

［1］張和明，柯映林，程耀東.參數曲面與平面求交的一種新方法［J］.工程圖學學報，1995（2）:31-37.

［2］張和明，張玉云，熊光楞，等.參數曲面與平面的精確求交及其應用［J］.機械工程學報，1997，33（5）:31-36.

［3］呂曉倩，趙玉剛，周海安.空間曲面與平面交線的一種插補算法［J］.組合機床與自動化加工技術，2008（3）:13-15.

［4］ROY U，DASARI R.Implementation of polygonal algorithm for surface-surface intersections［J］.Computers Industry Engineering，1998，34（2）:399-412.

［5］馬 翔，周儒榮.自由曲面與平面的一種分割、跟蹤求交方法［J］.南京航空航天大學學報，1994，26（1）:75-79.

［6］鄭立垠，張 麗，張云鵬.細分曲面求交交線計算方法的研究［J］.微計算機應用，2008，29（1）:78-81.

［7］余正生，李啟炎，肖少擁，等.一種直線與隱式曲面求交的方法［J］.工程圖學學報，2000，21（3）:20-23.

［8］ROTH S D.Ray casting for modeling solid［J］.Computer Graphics&Image Process，1982，18（2）:109-144.

［9］余正生，楚廣琳.一種跟蹤隱式曲面交線的算法［J］.計算機應用研究，2008，25（7）:2235-2237.

［10］宋宏勛，韓 毅，吳初娜.一種基于等值線法的NURBS曲面與平面的求交算法［J］.數字技術與應用，2011（7）:103-105.

［11］孫殿柱，孫永偉，田中朝，等.三角網格曲面模型快速求交算法［J］.北京工業大學學報，2012，38（8）:1121-1124.

［12］孫殿柱，康新才，李延瑞，等.三角Bézier曲面快速求交算法［J］.機械工程學報，2011，47（3）:89-94.

［13］PIEGL L.On NURBS:a survey［J］.IEEE Computer Graphics&Application，1991，11（1）:55-71.

［14］隆 強，謝延敏，楊 川.基于Foleg參數法反算三次NURBS曲線的算法研究［J］.機械，2012，39（7）:5-8，40.