船舶噪聲源的傳遞率矩陣識別方法及試驗驗證＊

張 磊，曹躍云，楊自春，何元安

（1．海軍工程大學動力工程學院，湖北 武漢 430033；2．中國船舶工業集團公司船舶系統工程部，北京 100036）

引 言

船舶的噪聲源識別或噪聲傳播途徑識別問題是噪聲控制中首要的也是最重要的工作［1］。通過振動噪聲源識別研究，可以有效估計船舶各個噪聲源對水噪聲（包括輻射噪聲和自噪聲）的貢獻量，及對噪聲源進行相應的空間定位。從而指導船舶減振降噪措施的正確實施和輔助噪聲系統的聲學設計和噪聲預報。另外，當機器或設備出現故障時，其聲信號特性一般會改變，因而通過噪聲源識別研究，也有助于對機器設備進行狀態檢測和故障診斷，可以及時地掌握機械的運行狀態，準確查找故障，提高船舶的聲學性能。

由于船舶結構及其工作環境的復雜性、特殊性，使其具有噪聲源耦合強烈、試驗實施難度大和測試信號易受環境干擾等特點，使得當前各種方法在實船噪聲源識別上的應用往往難以令人滿意［2］。目前解決此類噪聲源識別問題較為有效的方法是近年來在汽車噪聲源研究領域發展起來的傳遞路徑分析（Transfer Path Analysis，TPA）方法［3，4］，但其過程繁瑣、試驗復雜，且難以準確反映設備在運行狀況下的真實振動噪聲特性。為了避免上述缺點，一種基于傳遞率矩陣方法的噪聲傳遞路徑分析方法被提出［5］。隨著分析中主要應用運行工況時的響應數據，TMM 也被稱為工況 TPA（Operational Transfer Path Analysis，OPA）方法［6，7］。即使 TMM 具有眾多優點，但在實際工程應用中仍存在3種缺陷［7］：由于結構的模態影響，輸入振源間存在交叉耦合缺陷；實際工況的限制可能導致傳遞特性估計不準確；遺漏部分傳遞路徑，TMM的擬合總值對比不能識別。從TMM實際應用中的缺陷看，有必要對TMM進行改進，在保持效率的同時提高分析準確性。

1 TPA法與TMM的基本原理

TPA方法的基本原理是：機械設備工作狀態下輻射聲場中的聲壓響應值等于其與各噪聲源之間的頻響函數和工作狀態下各噪聲源處的激勵力乘積的疊加［3］，即

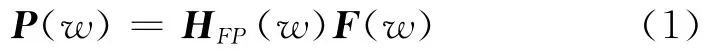
式中F（w）為工作狀態下的激勵力列向量；P（w）為工作狀態下聲場中聲壓響應的列向量；HFP（w）為各噪聲源到輻射聲場中聲壓響應的頻響函數，它不僅是激勵頻率的函數，還和響應點、激勵點的位置有關，但與激勵的幅值無關。

直接測量工作狀態下的耦合激勵力在實際操作中會遇到很多問題，間接測量法不需要嵌入力傳感器，這可以在一定程度上避免直接測量法的不足，因而它是工程中常用的方法。逆矩陣法就是一種有效的獲取耦合激勵力的間接法［3］，該方法需測量力／加速度傳遞函數，結合實測振動響應X（w），可獲得力估計為

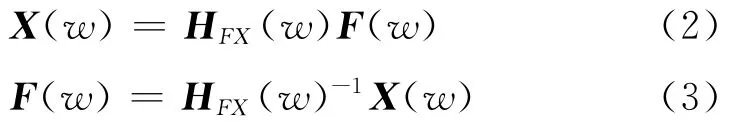
以上TPA方法在實際應用中將面臨很多問題，不利于工程應用。于是，將式（3）帶入式（1）得到基于TMM方程

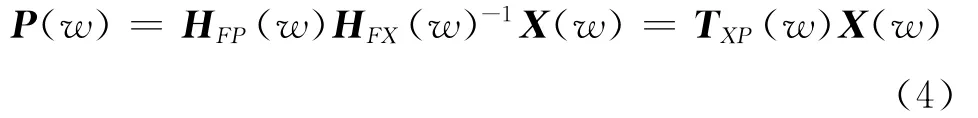
式中 振動輸入響應X（w）可以為力信號、振動加速度信號、聲壓信號、位移信號等。

TMM沒有進行載荷識別，而采用響應－響應的方式。由于結構的模態特性，一個激勵點的激振力將在其他路徑上引起振動，這種輸入信號之間有著較復雜的交叉耦合關系很容易導致主要路徑的識別錯誤。對于該問題，實際應用中主要結合一些先驗信息（如設備的特征頻率等），選取緊挨振源且振動響應較大，并能反映振源頻率較全面的振動加速度測點作為振源輸入。對于耦合性較弱的振源是可行的，但振源耦合性較強或振源測點在共振和反共振頻率時卻很難得到理想的效果。由式（1）和（2）可知，為了避免輸入振源之間的交叉耦合性，需滿足頻響函數矩陣HFX（w）為對角矩陣，即每個路徑處的振動響應X（w）僅與相應的激勵力有關。在船舶機械設備振源特性分析時，1kHz以下的低頻段內，可將機械設備和基座以及整個減振器的接觸單元認為是點接觸［8］。根據復剛度法［3］，主動方（設備）與被動方（基座）中間通過彈性件（隔振器）連接，耦合連接件與主動方和被動方的兩端連接處都產生位移。機械設備通過隔振裝置作用到基座，其工作力按下式求得

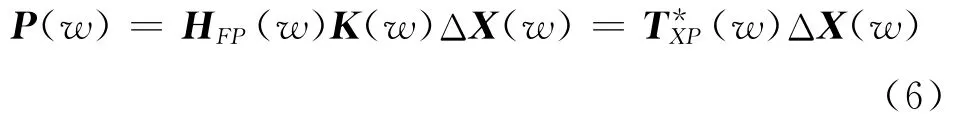
此處將隔振器兩端的位移響應之差ΔX（w）視為輸入振源，因HFX（w）－1＝K（w），可知HFX（w）為對角矩陣，即振源ΔX（w）在一定程度上避免了輸入振源之間的交叉耦合性。且只需要輸入輸出的加速度響應來求得傳遞函數矩陣（w），而不需要獲得復剛度矩陣K（w）或頻響函數矩陣HFX（w）。

TMM關鍵的一個部分就是計算系統的傳遞特性矩陣（w），該矩陣里所有元素都是從同一次試驗數據中得到的，所有的輸入都是在同一時刻進行的，將式（6）兩邊取轉置得

式中m，n表示輸入輸出的自由度數。如果定義船體結構系統的傳遞函數矩陣是線性時不變的，對于r個不同的測量工況滿足

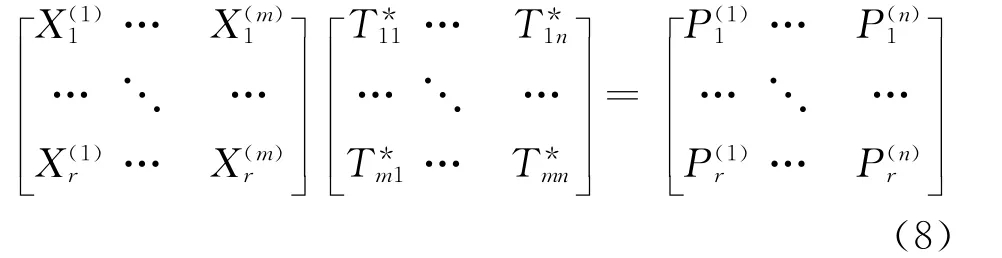
TMM是一種理論簡單且快速的方法，該方法僅需要運轉工況時振源響應和目標點的聲壓響應值。利用在不同工況下由振源測點到目標點的聲壓響應所形成的傳遞矩陣，即可分析每一個傳遞路徑對目標點的貢獻，進而識別出主要噪聲源。但實際工程應用中有效地實現TMM是非常困難的，仍面臨以下問題：

（a）輸入信號之間的相干性以及實際工況的限制產生病態矩陣求逆等問題，可能導致不可靠的傳遞特性估計。可采用截斷總體最小二乘（TTLS）方法避免矩陣求逆存在的不適定問題［9］，TTLS考慮了振源輸入矩陣ΔX和聲壓目標點矩陣P同時存在測量誤差，優于傳統的基于最小二乘（LS）的奇異值截斷方法。

（b）遺漏部分傳遞路徑，TMM合成總貢獻不能識別。可用重相干函數檢測是否有重要傳遞路徑被遺漏［10］，假設本文路徑數目均已知。

2 船舶振動－聲輻射仿真計算及結果分析

利用CAE技術進行船舶結構振－聲耦合計算，以驗證TMM在船舶噪聲源識別中的可行性與正確性。利用ansys創建船舶結構有限元模型（船長15 m，最寬處2．5m，高1m），如圖1所示。假設艙段內有5臺機械設備，設備1#，2#，3#在同一個艙段內，將振動設備等效為集中質量系統，在集中質量系統上施加的激勵載荷，每個集中質量系統通過4個彈簧－阻尼單元與甲板相連。利用Virtual．Lab對船舶輻射噪聲聲場指向性和輻射噪聲衰減進行仿真計算，可知與船舶夾角130°的軸線位上有最大輻射聲壓幅值。同時通過船舶輻射噪聲衰減仿真結果，與船舶垂直距離50～100m范圍內的聲場均滿足球面波衰減規律（遠場測量條件）。綜上，此次仿真將聲場測點位置選為軸長100m，與船夾角130°處。

基于Virtual．lab軟件進行船舶部分浸入水中（吃水深度0．5m）的聲振耦合計算，即先把聲場的一部分離散成聲學有限元網格，進行聲固耦合聲學有限元分析，接著在聲學有限元網格的外表面上定義聲學無限元，然后定義場點網格。最終獲得船舶振動響應和聲場中的聲壓響應，為貼合工程實際，數據處理時將加入隨機噪聲的影響。工況包括5臺振動設備同時作用和每個設備單獨作用，分析頻率f＝20～300Hz。

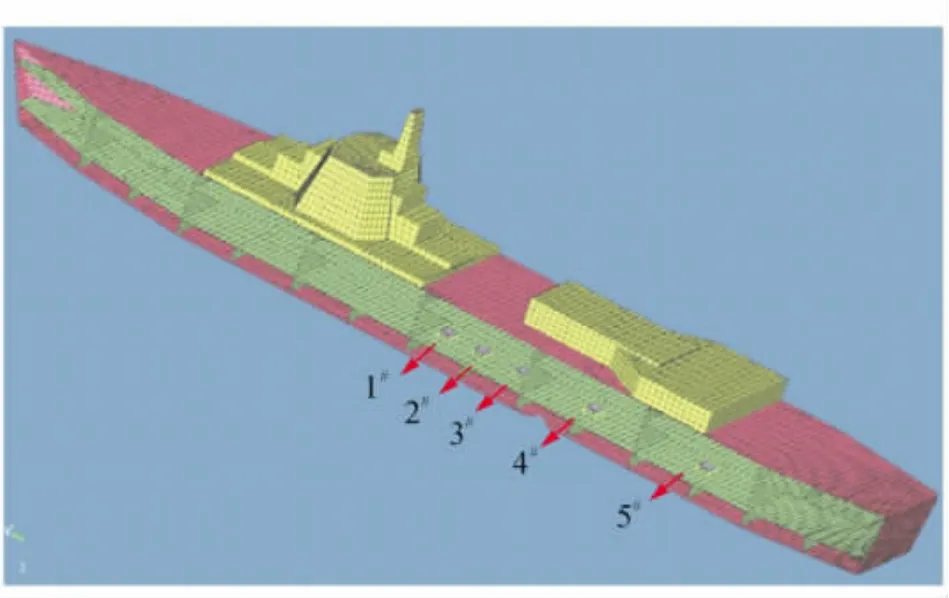
圖1 船舶結構有限元模型Fig．1 Finite element model of the ship structure

2．1 聲場噪聲合成與驗證

模型中一臺設備有4個機腳與甲板相連，選擇設備均布置規則且測點位置對稱。在低頻范圍內，通過設備單獨開啟，檢測設備各機腳測點振動響應之間的相干性，檢測發現：單個設備各測點之間在關注的頻段內相干性均較強（＞0．8），此時可選擇任一一個測點作為振源輸入，為保證信噪比，選擇振動響應最大的測點。再利用1節中提到的重相干系數檢測所有設備的振源測點對聲場目標點的相關性，在關注的頻段內各振源與目標點的重相干系數值均＞0．8，即可認為所選振源測點能夠反映目標點的所有信息［10］。通過 MATLAB編制TMM程序對5個振源在某一工況下到船外目標點聲壓貢獻量進行合成，基于兩種輸入振源的合成值與實際值均吻合非常好，如圖2所示。由于測得的數據在模型計算中被應用了兩次，合成聲與實測噪聲吻合較好并不能一定保證TMM的有效性。例如：由圖3，4可知，以加速度作為振源時，盡管總合成聲與實際吻合較好，但單條路徑對目標點的響應與實際值偏差較大。可見，只有在解決了1節中的幾個關鍵問題，結果才是可信的。假如不理解TMM的原理，將很容易被結果誤導。而本文以ΔX（w）作為輸入振源建立的模型在有效地解決了TMM應用中面臨的關鍵問題，結果可信，也證明了船外噪聲傳遞路徑模型和仿真計算模型的正確性。

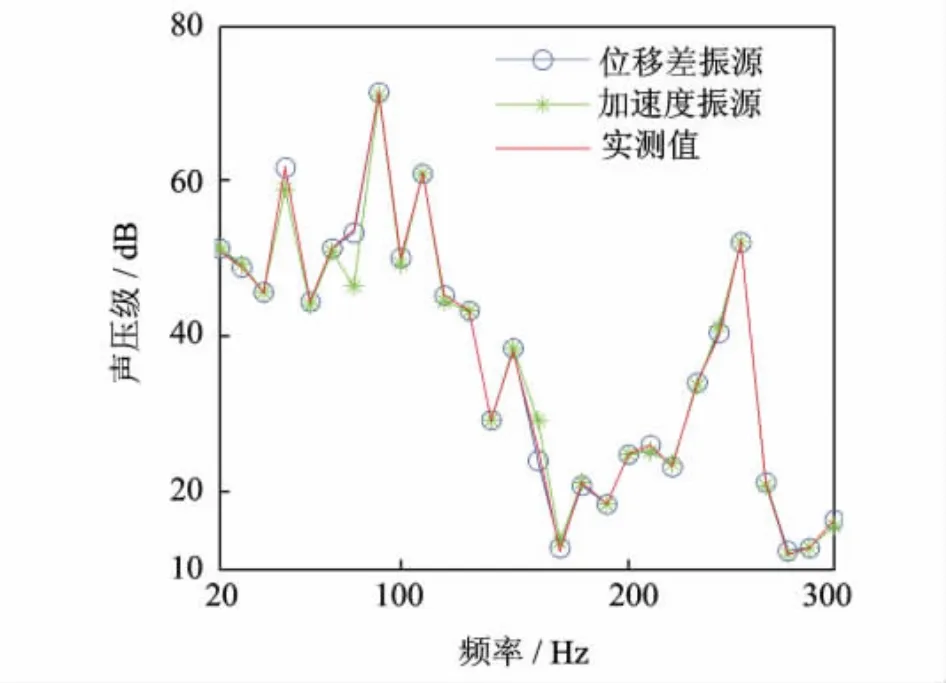
圖2 噪聲實測值與合成值比較Fig．2 Contrast of synthesized and actual noise

2．2 噪聲貢獻量分析

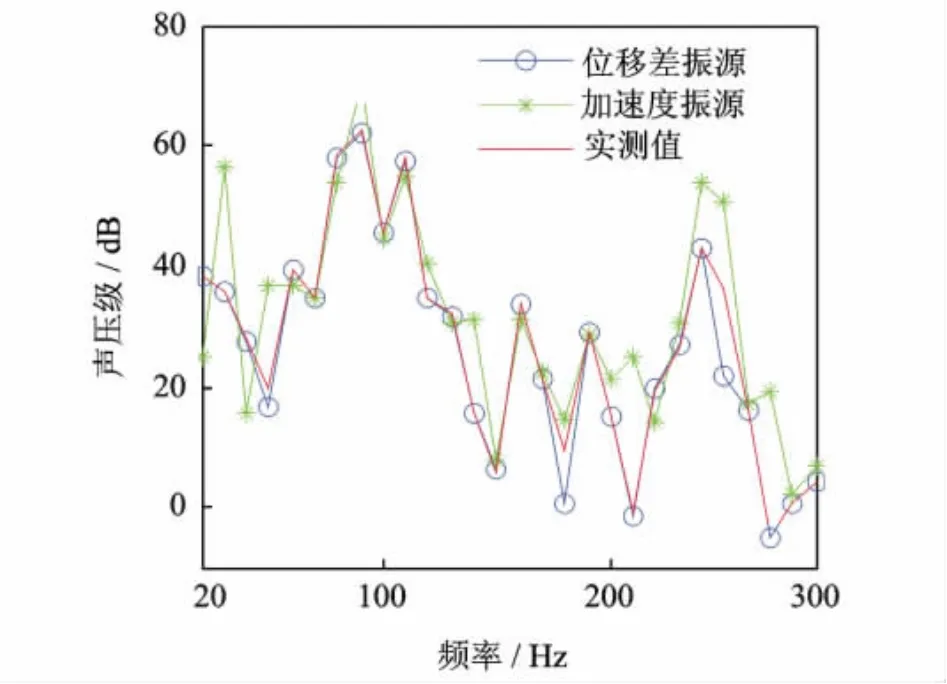
圖3 1#設備合成和實測噪聲對比圖Fig．3 Contrast of synthesized and actual noise of 1#

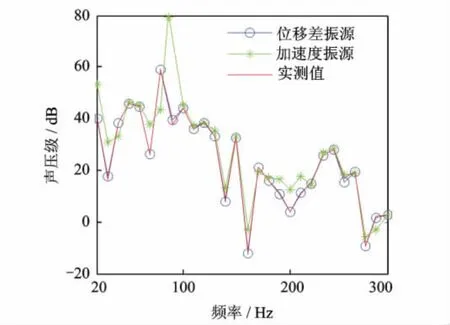
圖4 5#設備合成和實測噪聲對比圖Fig．4 Contrast of synthesized and actual noise of 5#

以加速度響應和本文引入的位移差ΔX（w）作為輸入振源時，1#和5#設備的路徑到目標點的合成噪聲與設備單獨開啟時船外目標點噪聲的對比如圖3和4所示。可以看出：以加速度作為振源時，由于受到了其他振源的交叉耦合作用，TMM合成結果與實際計算結果吻合較差。路徑5在一個獨立的艙內，其受到其他振源的耦合較弱，結果誤差較小。而路徑1受其他路徑的耦合作用較強，導致其誤差更大。由于低頻段各振源之間的交叉耦合性較強，圖中低頻時的結果要劣于高頻時的結果。圖中以ΔX（w）作為輸入振源可以在一定程度上避免振源間交叉耦合作用的影響，基于此振源的目標點噪聲合成值與實測結果吻合較好，除個別頻率點外，誤差均不超過3dB。以整個頻段的總聲壓級為基本量，5條傳遞路徑對目標點噪聲的總貢獻量排序分別為2#＞1#＞3#＞5#＞4#，此結果與分布運轉法得到的結果完全一致，證明了本文TMM在船舶機械設備噪聲源識別和貢獻量分析中的有效性。

3 實船海上振動－聲輻射試驗及數據分析

為了進一步驗證TMM在實船機械設備噪聲源識別中的有效性，本文進行了實船錨泊狀態下的振動－聲輻射試驗，試驗在水域寬闊的海上進行，背景噪聲滿足測試要求，試驗主要分析低頻段特性，主要測試的振動噪聲源為設備1、設備2、設備3。試驗首先采用便攜式振動設備在船內進行設備振動情況的預評價，為振源識別提供測點選取的基礎數據，然后在每個設備選擇2個典型的機腳，在每個機腳的隔振器兩端即設備和基座上分別各布置1個三向加速度傳感器，布置在緊挨機腳并盡量避免將測點布置在振型的節點處。試驗中共布置三向加速度計12個，在船外部指定水域指向性較大的方向布放3枚水聽器采集聲場數據，水聽器布放深度與設備所在位置基本保持同一水平面。試驗典型設備與傳感器示意圖如圖5所示。

圖5 典型設備與傳感器圖Fig．5 Typical equipment and sensors

試驗中船外的輻射噪聲與船體的結構振動數據實現了同時基采集，并對聲場信號進行了時延的修正。為有效地實現TMM，各設備在不同的轉速或負載的條件下工作，盡可能多的變化設備的工況組合，共測得了15組不同工況的組合，每組工況采樣6次。并對3臺設備分別單獨開啟，用以驗證TMM結果是否正確。

3．1 船外噪聲合成與驗證

使用便捷設備對各機腳的振動情況進行預評價，得出同一設備的各機腳間的振動相關性較強。因此，進行噪聲源識別時取每個設備一個機腳處的測點（為保證信噪比，優選振動響應較大的測點作為振源）。由于本文所選低頻段內的測試數據相干性較好，且該頻段受其他因素的干擾也相對較小，所以將隔振器與機械設備、基座接合部位按點接觸處理。考慮x，y，z向的振動傳遞即每個設備3個路徑點，總路徑點數m＝9。通過TMM程序對3個振源（9個路徑點）到船外目標點聲壓貢獻量進行合成，并與實測結果相比（選取一個信噪比較高的水聽器作為目標點），結果見圖6。可以看出，船外目標點的合成聲與實測噪聲的頻譜頻域分布基本一致，主要峰值頻率均能一一對應，且對應幅值吻合較好。通過TTLS修正的結果要優于LS修正的結果，即TTLS可以有效地緩解振動輸入矩陣ΔX在求逆過程中的不適定問題，有效地避免了振動加速度和聲壓響應的測量噪聲引起傳遞函數矩陣估計的不穩定。

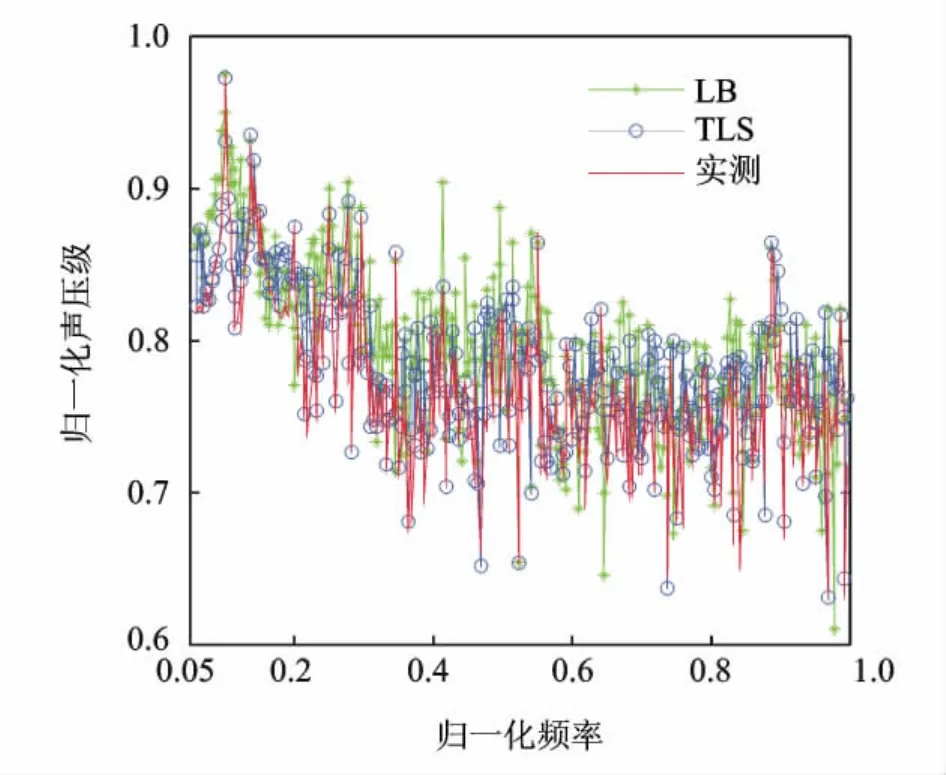
圖6 噪聲實測值和合成值比較Fig．6 Contrast of synthesized and actual noise

圖7為設備3在不同形式輸入振源條件下，船外目標點的噪聲合成值與實測值的比較圖。圖中以振動加速度作為振源時，因振源間存在耦合效應，計算誤差普遍偏大，在0．05～0．6的低頻段內尤為明顯。在頻率點0．2和0．65左右出現了較大的誤差，分析認為：可能由于設備1振動耦合所致。而以輸入位移之差ΔX（w）作為輸入振源時，可有效地減輕各路徑點間交叉耦合作用的影響，其主要峰值頻率點處噪聲合成值與實測值吻合較好，進一步證明了TMM方法的有效性。

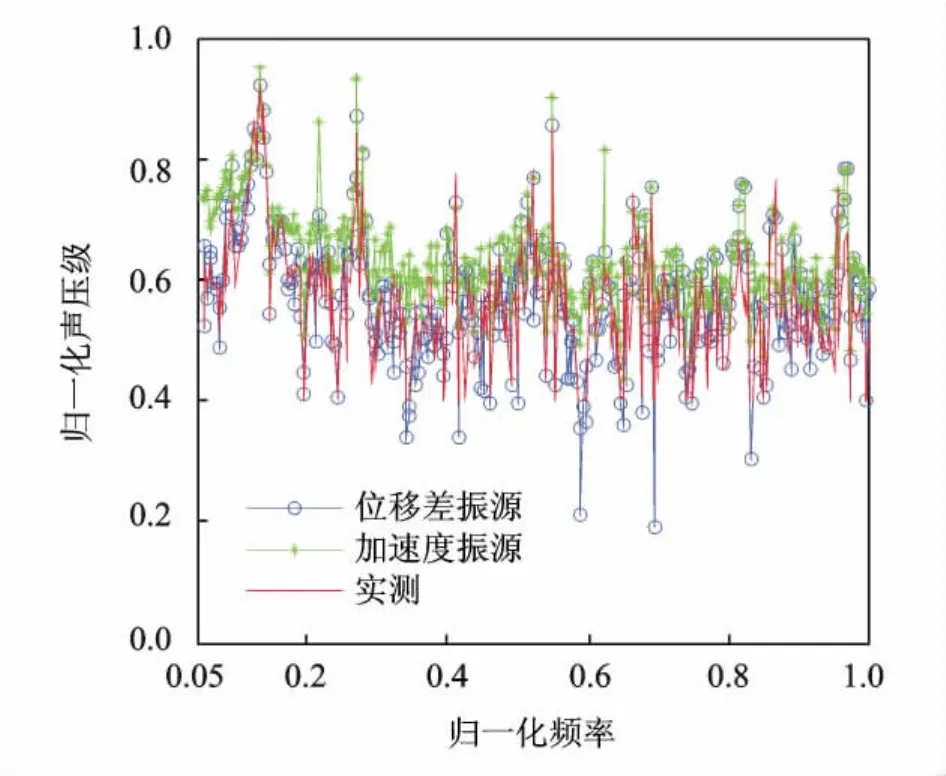
圖7 設備3合成和實測噪聲對比圖Fig．7 Contrast of synthesized and actual noise of 3#

3．2 噪聲貢獻量分析

為分析3個設備9條路徑對目標點的貢獻量，給出噪聲貢獻頻譜云圖如圖8所示。圖中顯示，y1，y2和z3路徑在整個頻段內具有較大貢獻，在0．15頻率點附近目標點的噪聲總合成較大，此處各路徑的貢獻量排序為z3＞y2＞y1＞z2＞x2＞x1＞x3＞y3＞z1。以頻點0．05到1整個頻帶內的聲壓級為基本量，得到各路徑的對目標點的噪聲貢獻量排序為z3＞y1＞x3＞z2＞x1＞z1＞y3＞x2＞y2，由此得出3個設備的總貢獻量排序為設備3＞設備2＞設備1，該結果與某設備單開的實測結果完全一致。可見，TMM方法在噪聲貢獻量排序分析中具有較高的可靠性，且可對關心的單個頻率點或頻帶進行針對性的分析，適用性更強。

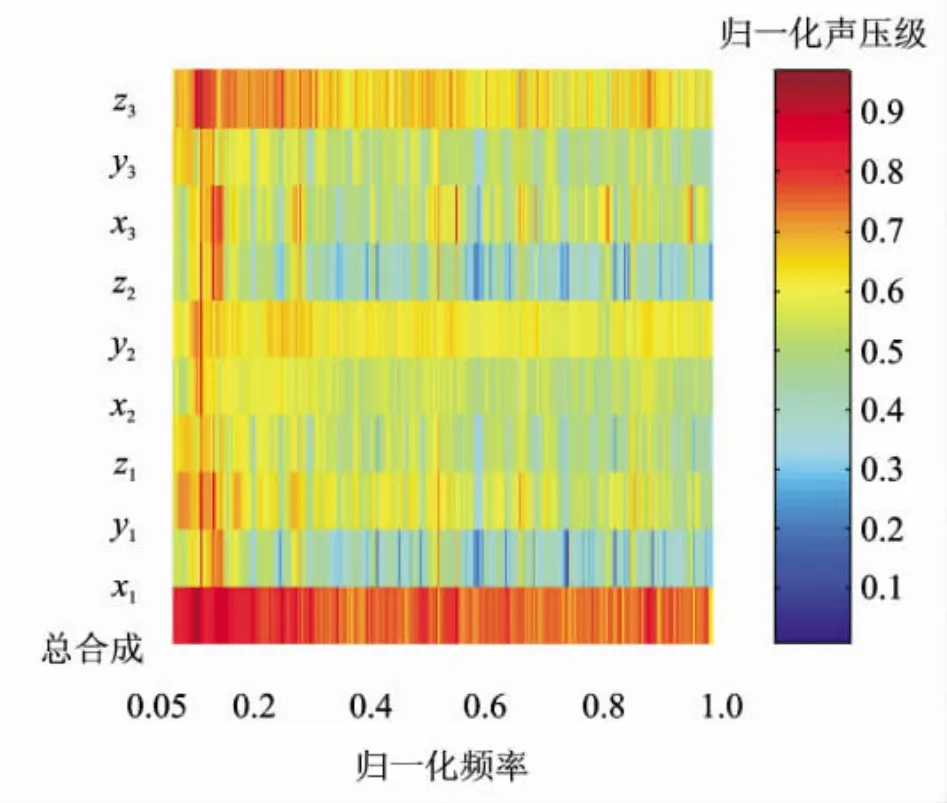
圖8 噪聲頻譜云圖Fig．8 Cloud map of noise frequency spectrum

利用噪聲的貢獻譜圖分析時，值得注意的是，一條具體的傳遞路徑所傳遞的能量引起的聲壓貢獻與幅值和相位相關，如圖8中存在某些頻率點處各路徑均有較大的貢獻，但是總的貢獻量依然很小，這可能是由于不同路徑之間的相位反向，使得總的貢獻量降低。因此，在進行傳遞路徑分析時，先弄清楚各路徑所傳遞噪聲的相位是特別重要的。

由圖9貢獻量的極坐標圖可分析各傳遞路徑的幅值和相位對目標點聲壓響應的影響，圖中以目標點總合成噪聲的相位116．6°為基準相位，即圖中x向。可見，傳遞路徑矢量和x向夾角越小對總合成的影響越大，當與x向同向時，增加目標點的噪聲總合成值；反之，抵消了總合成的噪聲值。在進行噪聲源及其傳播路徑的識別和控制時，要特別注意與x向夾角小且幅值大的傳遞路徑，如圖中傳遞路徑z1，y2，z2，x2，y3，z3對目標點的噪聲響應起增強效果，傳遞路徑x1，y1，x3對目標點的噪聲響應起削弱效果。綜上，在機械噪聲源識別和貢獻量排序時，考慮各傳遞路徑的幅值和相位的影響更符合實際情況，且更有利于減振降噪措施的正確實施。

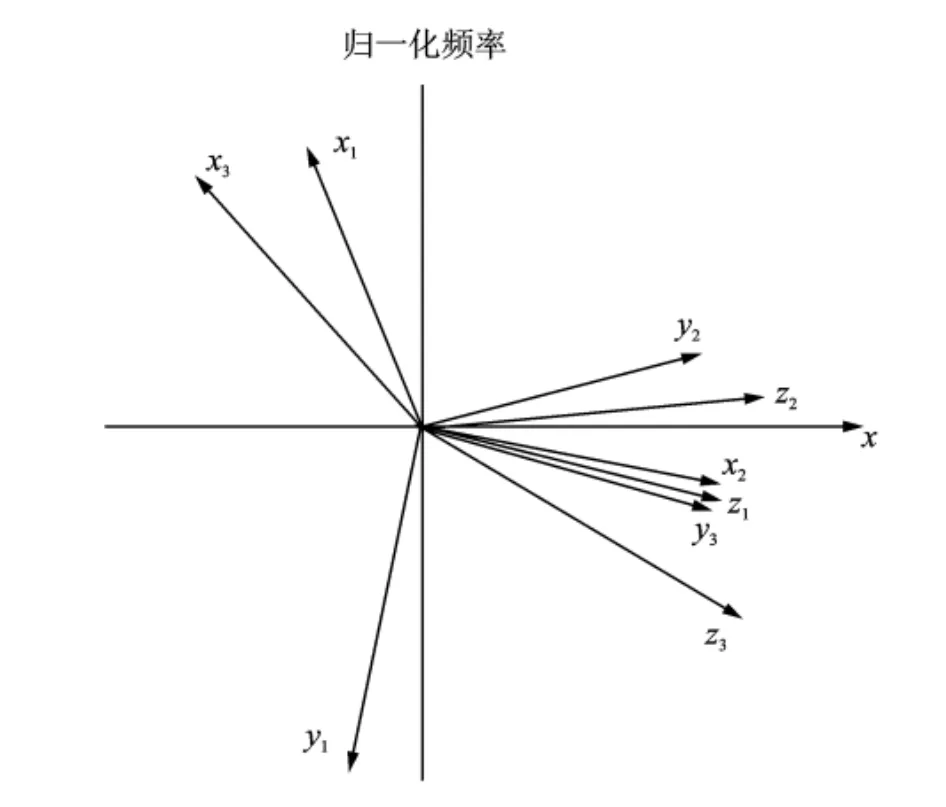
圖9 各路徑貢獻的矢量圖Fig．9 Vector superposition of each transfer path

4 結 論

傳遞率矩陣方法（TMM）在船舶噪聲源識別中具有快速、理論簡單和真實反映設備運行特性等優點，這些優點都是傳統方法難以比擬的。但在實際工程應用中該方法仍存在缺陷，文章全面分析了這些缺陷并提出解決方案，重點解決了振源間存在交叉耦合的缺陷。基于TPA理論提出一種新的基于傳遞率矩陣方法（TMM）的噪聲傳遞路徑分析模型，通過船舶水中振動－聲輻射仿真分析和實船海上振動－聲輻射試驗對新模型進行驗證。結果顯示，該模型有效地避免了輸入振源之間的交叉耦合，能夠高效、準確地進行船舶噪聲源識別和貢獻量分析，進而指導船舶的聲學設計和噪聲預報，同時為船舶的振動噪聲治理提供有效的依據。

［1］ 楊德森．水下航行器噪聲分析及主要噪聲源識別［D］．哈爾濱：哈爾濱工程大學，1998．

YANG Desen．Noise sources identification and analysis for underwater vehicles［D］．Harbin：Harbin Enginerring University，1988．

［2］ 章林柯，何琳，朱石堅．潛艇主要噪聲源識別方法研究［J］．噪聲與振動控制，2006，（4）：7—10．

ZHANG Linke，HE Lin，ZHU Shijian．Review on the methods of identification of submarine main noise sources［J］．Noise and Vibration Control，2006，（4）：7—10．

［3］ Knapen P L．Transfer path analysis related to booming，performed on a car［D］．The Netherlands：Eindhoven University of Technology，2006．

［4］ 田雄，李宏成，呂先鋒，等．基于傳遞路徑試驗分析的變速器敲擊噪聲優化［J］．振動工程學報，2010，23（6）：642—648．

TIAN Xiong，LI Hongcheng，LU Xianfeng，et al．A study on transmission rattle noise optimization based on transfer path test analysis［J］．Journal of Vibration Engineering，2010，23（6）：642—648．

［5］ Noumura K，Yoshida J．Method of transfer path analysis for interior vehicle sound by actual measurement data［A］．Proceedings of JSAE Annual Congress［C］．Yokohama，Japan，2006：7—12．

［6］ Klerk D D，Ossipov A．Operational transfer path analysis：Theory，guidelines and tire noise application［J］．Mechanical Systems and Signal Processing，2010，（24）：1 950—1 962．

［7］ Gajdatsy P，Janssens K，Desmet W，et al．Application of the transmissibility concept in transfer path analysis［J］．Mechanical Systems and Signal Processing，2010，（24）：1 963—1 976．

［8］ 原春暉．機械設備振動源特性測試方法研究［D］．武漢：華中科技大學，2006．

YUAN Chunhui．A study on the test approaches of characterization of machinery as vibrational sources［D］．Wuhan：Huazhong University of Science and Technology，2006．

［9］ Diana M S，Sabine V H．Level choice in truncated total least squares［J］．Computational Statistics and Data Analysis，2007，52：1 103—1 118．

［10］Qiu Y，Griffin M J．Transmission of vibration to the backrest of a car seat evaluated with multi－input models［J］．Journal of Sound and Vibration，2004，274：297—321．