非線性結構動力學系統的首次穿越
任麗梅,徐 偉,李戰國
(西北工業大學理學院,陜西西安 710072)
在地震工程,橋梁工程等領域中動力學系統的結構可靠性一直是研究的熱點,而受到諸如地震、風及海浪等隨機激勵的動力學系統的首次穿越失效更是研究的焦點之一。首次穿越失效概率(簡稱:首穿失效概率)是結構安全性的重要指標,是指在某個時間段內結構響應首次超過指定安全域邊界的概率。盡管這個問題已經得到了高度重視,但仍是結構安全性分析最具挑戰性的問題,因為直到現在,即使是最簡單的線性振子場合也無可利用的精確解。
自Rice[1-2]的開拓性研究以來,研究者雖然提出了基于Fokker-Planck方程的路徑積分法、胞映射法、有限元等數值解法[3-5],但這些方法的復雜度隨狀態空間維數的增加呈指數增加趨勢,因此普遍認為等效線性化與基于方差縮減技巧的蒙特卡羅模擬方法是解決此類問題的選擇[6],研究者據此先后提出重要抽樣法,受控蒙特卡羅法[7],子集模擬法[8],區域分解法[9]等,在方差縮減技巧中基于Gisranov定理的重要抽樣法[10-15]已經被廣泛應用。
基于Gisranov定理的重要抽樣法可以描述為一種控制樣本路徑的方法:樣本被集中在樣本空間中最重要的部分,而不是均勻分布在樣本空間中。然而達到這樣的目的選擇怎樣的控制函數才是最關鍵的。在許多的研究中均是利用設計點來構造控制函數的,但僅在穩態高斯白噪聲激勵的線性系統場合,設計點具有解析表達式,在非線性系統場合,設計點的得到通常采用近似方法[16-18]。可是設計點的準確性直接影響到控制函數的控制功能,因此本文利用線性系統具有解析的設計點這一特性,首先根據Rice公式,得到與非線性系統方程具有相同平均上穿率的等效線性化系統方程,利用此等效線性化方程得到設計點的解析表達式,構造控制函數。然后將控制函數運用到非線性系統方程中。利用重要樣本法估計非線性系統的首穿失效概率。最后文章以Duffing振子為例,模擬結果顯示了方法的正確性與有效性。
1 重要樣本法
設結構動力學系統響應是一p維向量X(t)=[X1(t),X2(t),…,Xp(t)]T且滿足 Ito^隨機微分方程:
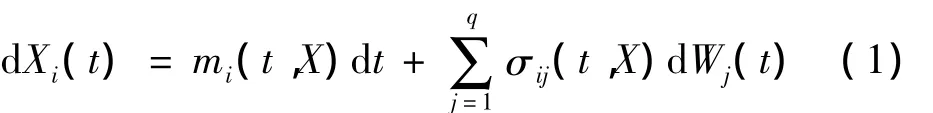
Xi(0)=xi,其中W(t)=[W1(t),W2(t),…,Wq(t)]T是具有概率測度p的標準Wiener過程。m(t,X),σ(t,X)是漂移、擴散系數,分別滿足李普希茲條件和增長性條件[19]。定義系統的安全域是D∈Rp。
首穿失效概率為
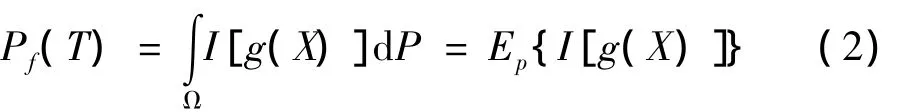
其中I[g(X)]是示性函數,
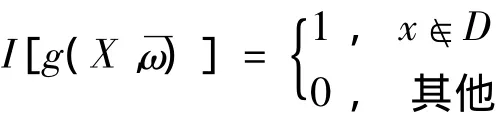
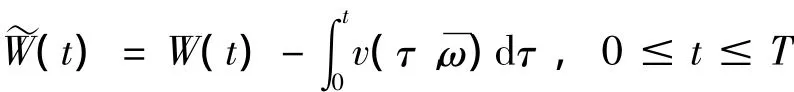
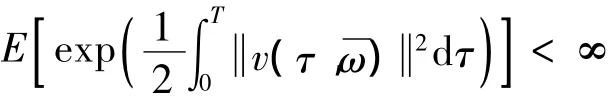
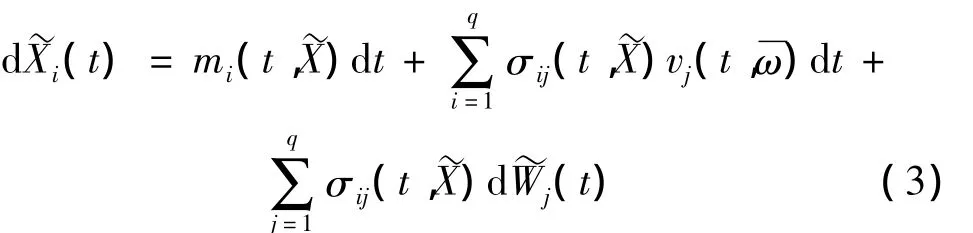
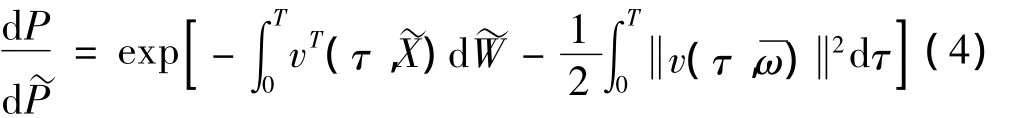
則在確定的初始條件下,基于概率測度 ~P的首穿失效概率的估計為
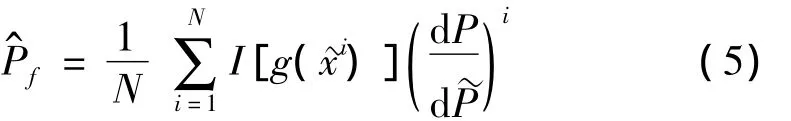
2 等效線性化
考慮零均值,具有單邊譜密度G0的穩態高斯白噪聲激勵的Duffing振子:
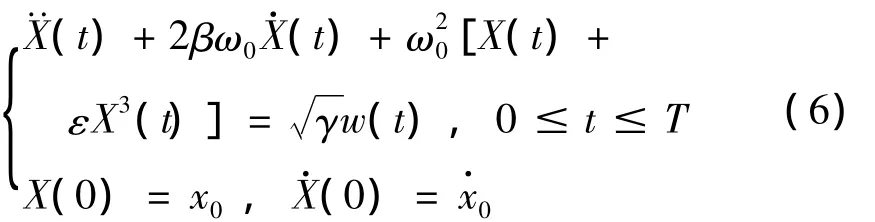
(x(t)(t))的穩態概率密度函數為
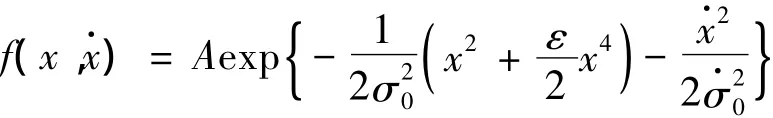

根據Poisson假設,利用Rica公式[19],非線性方程的平均上穿率為:
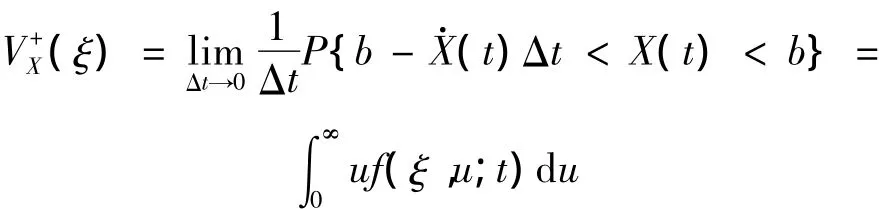
即:
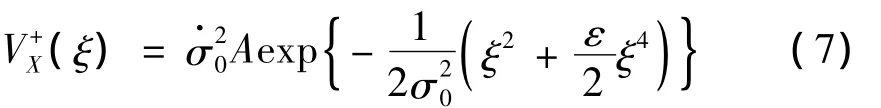
等效線性方程設為:
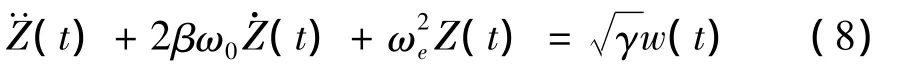
平均上穿率為:
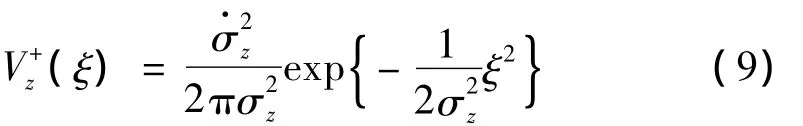
其中:
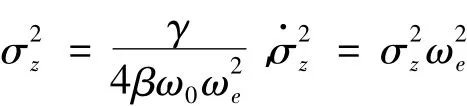
則解方程:

可得關于安全域邊界b的等效線性化參數ωe值。當非線性系統的平均上穿率無法得到解析表達式時,可以利用數值方法。蒙特卡羅方法也可以用來估計平均上穿率,在穩態過程場合平均上穿率被定義為:
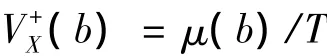
其中:μ(b)表示在時間間隔T內,穩態過程越出安全域的平均次數。
3 控制函數的構造
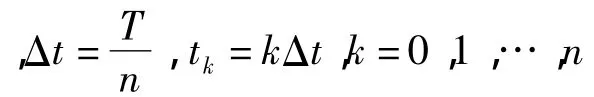
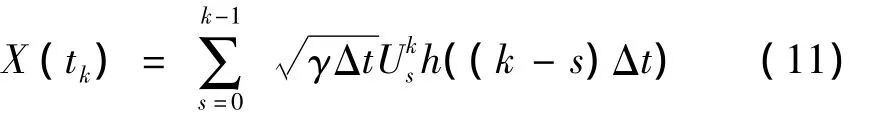
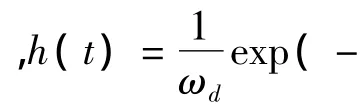
在tk時刻,極限狀態方程為:
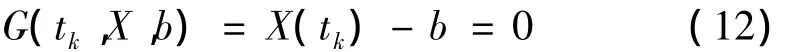
可靠性指標:

可得設計點為:
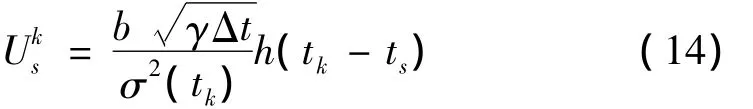
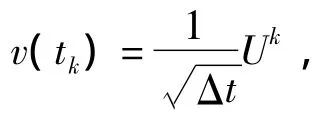
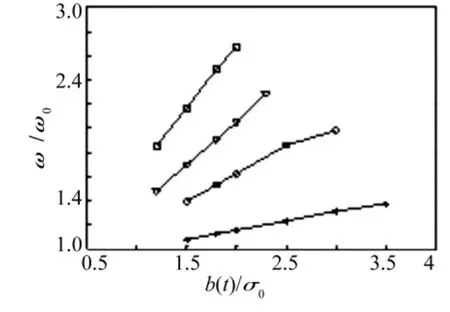
圖1 等效線性化參數與安全域邊界Fig.1 The frequencyvs threshold depending on different values of the non-linearity parameter ε.ε =0.1(*)ε=0.5(○),ε=1(△),ε=2(◇)
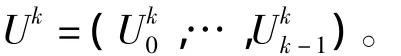
4 結果與討論
振子方程如式(6)所示,可令X1(t)=X(t),X2(t)=(t),其Duffing振子的It o^隨機微分方程為:
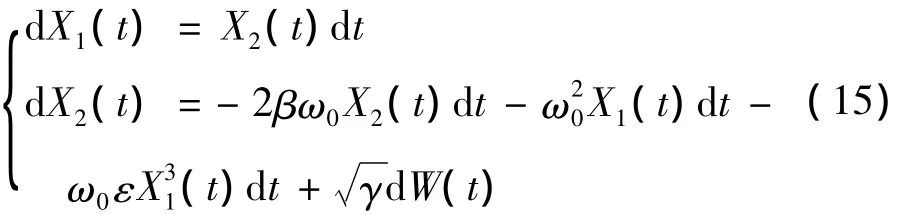
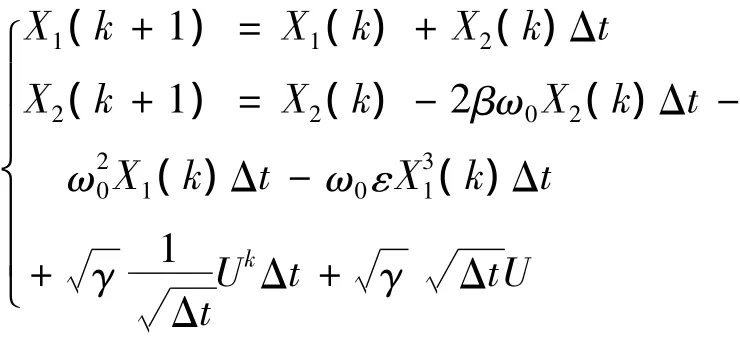
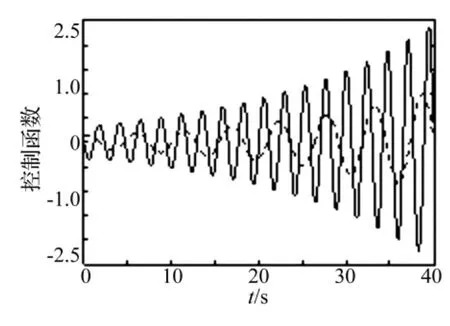
圖2 控制函數圖。ε=0.1虛線,ε=2實線Fig.2 Control function for an up-crossing of level b(t)=2.449 40 at time T=40 s.ε =0.1(dotted line),ε=2(solid line)
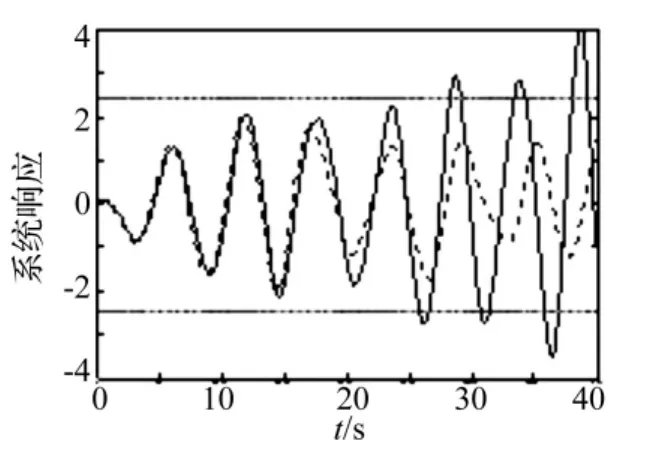
圖3 加控制(實線)與不加控制(虛線)的系統(ε=0.1)響應比較圖:Fig.3 The response of the non-linear system(ε =0.1)comparison chart:Add control(solid line)and not controlled(dotted line)
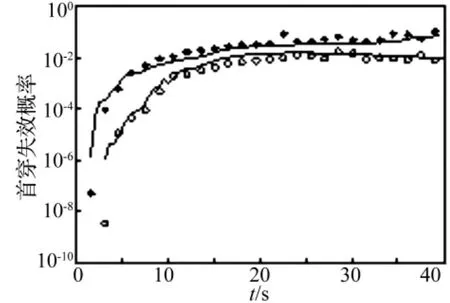
圖4 失效概率圖,b(t)=2.449 40,ε=0.01(* 線),ε=2(○線),原始蒙特卡羅法(實線)Fig.4 The first failure probability simulation comparison chart importance sampling procedure(ε =0.01(*),ε=2(○)),crude Monte Carlo(solid line)
在穩態高斯白噪聲激勵的Duffing振子中,令β=0.05,ω0=1.0(rad/s),γ =0.3,T=40 s,Δt=0.05,n=800,安全域邊界取常數邊界b(t)=kσ0。圖1是當非線性參數分別為 ε =0.1,ε =0.5,ε =1,ε =2 時,不同安全域邊界下等效線性化參數ωe與ω0的比值的示意圖。圖2是當ε=0.1(虛線),ε=2(實線)的控制函數圖。圖3是當ε=0.1時Duffing振子加控制(實線)與不加控制(虛線)的系統相應比較圖。從圖3中可看出在20 s之前加控制與不加控制的系統響應大致相同,20 s之后控制函數力量強勁,起到了支配的作用,與振子達到共振頻率,使得振子在26 s時首次越過安全域邊界b(t)=2σ0=2.449 40。圖4是在安全域邊界為b(t)=2σ0時,利用重要樣本法 ε=0.01(* 線),ε=2(○線)(N=103)時的首穿失效概率與原始蒙特卡羅(實線,N=106)法的比較圖,顯示了兩者很好的吻合,說明本文所提方法的正確性與有效性。
5 結論
本文基于Gisranov定理,提出了非線性結構動力系統首穿失效概率的重要抽樣法。本文利用線性系統具有解析的設計點這一特性,根據Rice公式,得到非線性系統的等效線性化方程,等效線性化原理采用平均上穿率而非mean square原理,研究者A.Naess也在研究首次穿越失效問題中采用了此線性化原理,他也認為此線性化原理對研究首穿問題是更加合理的。利用等效線性化方程得到解析的設計點,構造控制函數。然后將控制函數運用到非線性系統方程中,非線性系統不同非線性化參數ε下進行了模擬,結果說明了方法的正確性與有效性,且本文方法所需樣本量及計算時間遠少于蒙特卡羅模擬。
[1] Rice O C.Mathematical analysis of random noise[J].Bell Syst Tech J,1944(23):282-332.
[2] Rice O C.Mathematical analysis of random noise[J].Bell Syst Tech J,1945(24):46-156.
[3] Spencer B F,Bergman L A.On the numerical Solution of the Fokker-Planck equation for nonlinear stochastic systems[J].Nonlinear Dynamic,1993(4):357-372.
[4]Li W,Xu W.Stochastic optimal control of first passage failure for coupled Duffing-Van derPol system under Gaussian white noise excitations [J].Chaos.Solitons& Fractal,2005,25(5):1221-1228.
[5]Li W,Xu W.First passage problem for strong nonlinear stochastic dynamical system[J].Chaos.Solitons & Fractal,2006,28(2):414-421.
[6]Proppe C,Pradlwarter H J,Schueller G I.Equivalent linearization and Monte Carlo simulation in Stochastic dynamics[J].Probab Eng Mech,2003,18(3):1-15.
[7] Pradlwarter H J,Schueller G I.Assessment of low probability events of dynamical systems by controlled Monte Carlo simulation[J].Probab Eng Mech,1999,14(3):213-227.
[8] Zuev K M,Katafygiotis L S.The Horseracing Simulation algorithm for evaluation of small failure probabilities[J].Probab Eng Mech ,2011,26(2):157-164.
[9]Katafygiotis L,Cheung S H.Domain decomposrtion method for calculating the failure probability of linear dynamic systems subjected toGaussian stochasticloads[J].Journalof Engineering Mechanics,2006,20:475-486.
[10] Olsen A I,Naess A.An importance sampling procedure for estimating failure probabilities of Non-linear dynamic systems subjected to random noise[J].J Non-linear Mech,2007(42):848-863.
[11] Juu O,Hiroaki T.Importance sampling for stochastic systems under stationary noise having a specified power spectrum[J].Probab.Eng.Mech.,2009,24(4):537-544.
[12] Au S K,Beck J L.First excursion probability for linear systems by very efficient importance Sampling[J].Probab.Eng.Mech.,2001,16(3):193-207.
[13] Macke M,Bucher C.Importance sampling for randomly excited dynamical systems[J].J.Sound Vibration.2003,268:269-290.
[14] Olsen A I,Naess A.An importance sampling procedure for estimating failure probabilities of dynamic systems[C]//ASCE,Joint Speciality Conference on Probabilistic Mechanics and Structural Reliability,2004.
[15] Pradlwarter H J,Schueller G I.Excursion probabilities of non-linear systems[J].Int.J.Non Linear Mechanics,2004,39:1447-1452.
[16] Der Kiureghian A.The geometry of random vibrations and solutions by FORM and SORM[J].Probab.Engng.Mech.,2000,15(2):81-90.
[17] Liu P L,Der Kiureghian A.Optimization algorithms for structural reliability[J].Structural Safety,1991,9(3):161-177.
[18] Zhang Y,Der Kiureghian A.Two improved algorithms for reliability analysis[C]//Rackwitz et al,editor.Proceedings of the 6thIfIP WG 7.5 conference on optimization of structural systems,1994:297-304.
[19] Soong T T,Grigoriu M.Random vibration of mechancial and structural systems[M].Prentice-Hall.Inc.Englewood Cliffs,NJ,1997.

