基于Petri網的顧及轉向延誤的最優路徑算法

楊 琰，廖偉志，李文敬，楊 文，李 杰

（廣西師范學院 計算機與信息工程學院，廣西 南寧530023）

0 引 言

城市道路交叉口轉向引起的時間延誤不能忽略。有調查表明，城市交通網絡中車輛在交叉口的延誤可以達到全部行駛時間的17%－35%。考慮轉向延誤的最短路徑算法［1］具有重要的現實意義。針對這一問題國內外有些代表性的研究成果：唐小勇［2］和杜牧青［3］從數據存儲結構和算法兩方面著手求解最優路徑；高明霞［4］為網絡中的各個弧設置了一個距離標號和緊前弧標號，通過不斷迭代、更新弧的標號來尋找最短路徑；鄭年波［5］把交通路網表達為動態對偶網絡，推導了滿足先進先出特性的動態行程計算方法，設計了時間依賴的標號設定最短路徑算法。

現有的這些研究均針對有向網絡，然而現實交通網絡是無向的。當網絡規模增大時，無向圖向有向圖的轉化以及轉換后網絡結構的規模會導致問題求解的復雜度急劇增加。再者，目前常用的擴展網絡法和對偶網絡法均需對初始網絡進行變換，處理過程復雜且其處理結果將原本直觀的網絡結構變的不再一目了然。基于Petri網的最短路算法［6］是通過求解網圖中 “托肯”從指定起點到達終點的最短運行時間來尋求最短路徑，較傳統直接計算路長而言，更為直觀和方便。據此，本文針對雙向通行的交通網絡，提出基于無向Petri網［7］的顧及轉向延誤的最優路徑智能搜索算法。

1 基于無向Petri網的交通網絡模型

1.1 Petri網概述

Petri網 （PN）［8］是一種進行系統分析和模擬的圖形化建模工具，它既能刻畫系統的結構，又能模擬系統的運行，適合描述離散事件的動態過程。Petri網由基網 （net）和標識組成，網的部分描述系統的結構，標識部分表示系統的狀態。一個Petri網是一個四元組Σ＝ （S，T；F，M），其中：

（1）S＝ ｛s1，s2，…，sm｝是非空有限庫所集；

（2）T＝ ｛t1，t2，…，tn｝是非空有限變遷集，且S和T不相交；

（3）F （S×T）∪ （T×S）是流關系，且dom （F）∪cod（F）＝S∪T；（S，T；F）構成一個有向圖；

（4）W：F→N 是權函數。W （s，t）＝i（i＞0）當且僅當存在一條從庫所s到變遷t的權值為i的弧；W （s，t）＝0當且僅當不存在從庫所s到變遷t的弧。用t＝ ｛s｜ （s，t）∈F｝表示變遷t的輸入庫所的集合，s＝ ｛t｜ （s，t）∈F｝表示庫所s的輸出變遷的集合。

（5）標識M用一個m維 （m為網中庫所的個數）的非負整數向量表示。

對于變遷t∈T，如果s∈S：s∈t→m （s）≥1，則稱變遷t在標識M 有發生權 （enabled），記為M ［t＞。

1.2 擴充的Petri網 （Extended Petri Net）

由于顧及到道路交叉口的轉向延誤，用基本Petri網難以描述和計算，因此有必要對托肯 （token）和變遷 （transition）的使能規則進行擴展。

1.2.1 托肯的附加描述

Petri網圖中的托肯只有一種狀態，用庫所中的小實心圓點 “·”表示。在交通運輸網絡中，通常表示 “車輛或者人處于此位置”。現賦予托肯另外兩種狀態：一種表示“托肯處于轉向耗時中”，用內部加一小黑點的小圓 “⊙”表示；另外一種表示 “托肯處于路途耗時中”，用大的實心圓點 “●”表示。庫所中托肯的狀態變化如圖1所示。

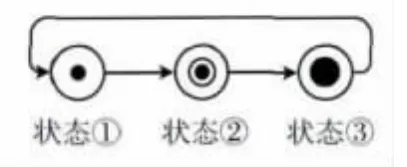
圖1 托肯的狀態變化

說明：狀態①：表示車輛或者人處于此位置；狀態②：表示托肯在進行 “轉向耗時”，或 “轉向耗時”剛完成；狀態③：表示托肯在進行 “路途耗時”，或 “路途耗時”剛完成；狀態③→狀態①：表示托肯 “路途耗時完成”，進入輸出庫所。

1.2.2 變遷的使能規則

規則1：若狀態①的托肯位于庫所p中，則所有以p為輸入庫所的變遷t的實施都是可能的。

規則2：從第0時刻開始計時，當托肯第一次到達庫所q時，將q（t）（t為托肯進入q的時刻）存入集合A。此托肯途經的庫所序列就是從起點出發到q的最優路徑序列，其時間消耗為t。此后所有以A中任一元素為輸出庫所的變遷均不能使能。

作用有二：因網絡無向，可以防止查找方向逆回去；若q屬于A，則表明從起點S到q的最優路徑已經產生，其余尚未到達q而準備朝q方向的查找將沒有意義 （滿足整體最優，則局部也最優）。

規則3：若托肯在向庫所q移動的 “耗時 （轉向耗時或路途耗時）”過程中，有其余托肯率先進入了q，則該托肯所代表路徑上相應變遷的使能終止，托肯移出網絡；當兩個或兩個以上來自不同庫所中的托肯準備在同一時刻移入到同一輸出庫所時，只保留其中一個，其余的移出網絡。

假設有3個來自不同庫所的托肯要同時進入輸出庫所q，這表明從起點S到達節點q的最優路徑有3條。

1.3 限制搜索區域的思想

經典Dijkstra算法按節點距起始點距離遞增的順序產生最短路徑，搜索的區域理論上是一個以起點S為圓心，M （人們所能接受的從S到終點D的極限距離）為半徑的圓。這種方法忽略實際交通網絡本身特有的空間分布特性，盲目的搜索導致大量與結果無關的節點引入計算，嚴重影響算法的效率。實際城市路網結構比較規則，特別是經過規劃的現代化都市。在城市路網路徑規劃研究中，合理的限制搜索區域［9］理論上可以提高路徑搜索的效率。

根據幾何知識：到兩定點的距離之和不超過某一確定值 （大于兩定點間的歐氏距離）的點的集合，構成了以這兩個定點為焦點、確定值為長軸長的橢圓。橢圓外的節點與結果無關，因此智能算法將搜索范圍鎖定在此橢圓區域內。設網絡中一點N到S和D的歐氏距離分別為｜SN｜、｜DN｜，則限制橢圓搜索區域的數學表示為：｜SN｜＋｜DN｜≤M 。

圖2所示為經典Dijkstra算法和限制橢圓的搜索區域對比圖。很明顯，限制區域后算法所需掃過的范圍要小很多，并且這種差別會隨著交通網絡規模及起終點間距離的增大而變得更加明顯。

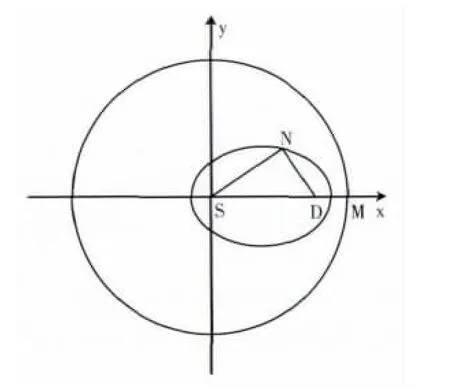
圖2 圓和限制橢圓搜索區域對比

1.4 無向交通運輸網絡的Petri網表示

Petri網圖是由 （S，T；F）決定的有向二元圖。圖中庫所節點s用圓表示，變遷t用帶箭頭的短線表示。將交通運輸網絡中相異路徑上相交的站點抽象為Petri網結構中的庫所s，不同站點間相連通的路徑抽象為變遷t。變遷的激發表示車輛離開當前站點，沿著變遷所代表的路徑向與其連接的另一站點前進。變遷上的權值表示相鄰站點間的距離、路途消耗時間等。將交通網絡中所有站點和路徑信息都體現在Petri網結構中就形成了交通運輸網絡的Petri網模型［10］。

本文針對雙向通行的交通網絡，故模型中連接庫所和變遷的弧是無向的。現實中的交通網絡是實時動態的，若某時段某路段限行，則只需隨時對數據庫中相應的弧段權值進行更新或增加限制即可。

圖3是由23個站點及36條雙向通行路徑構成的交通網絡的Petri網表示。站點抽象為庫所集P＝ ｛a，b，c，…，v，w｝，路徑抽象為變遷集T＝ ｛tab，tba，tad，tda，…，tgw，twg｝。變遷上的權值表示車輛通過相鄰站點所需的時間（單位：min）。假設起點為a，目標點為i，車輛在道路交叉口右轉、直行和左轉的平均延誤時間分別為0、2和3。設M值為50，用｜SN｜ ＋ ｜DN｜≤M計算得到的限制橢圓搜索區域如圖3中陰影部分所示。

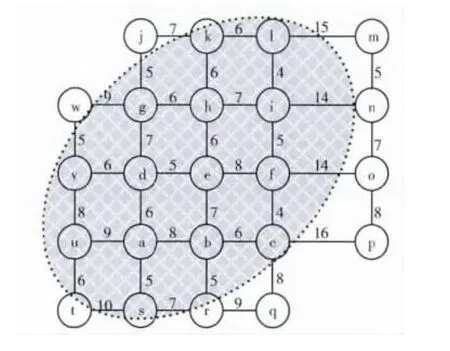
圖3 交通網絡的Petri網表示

2 智能算法

2.1 算法原理

首先通過合理限定橢圓區域把對網絡節點的搜索范圍縮小，然后根據1.2小節中變遷的使能規則1和2，在所有可能實施的變遷中選擇符合條件的那些變遷激發。同一時刻不同托肯的狀態代表著各自所探索路徑的耗時 （轉向或者路途耗時）狀況。搜索過程中根據規則3，及時地終止一些無意義的查找。程序按照使能規則有序發生，直到目標庫所中擁有托肯。算法通過計算機仿真托肯在網圖中從起點到達目標點的最短運行時間來尋求最優路徑，到達目標點的托肯所途經的庫所序列即為最優解。以圖3為例，求解從a到i的最優路徑問題就轉換成了求解起始庫所a中的托肯經過一系列變遷到達目標庫所i的最短時間消耗問題。

2.2 數據的準備工作

數據的準備工作包括5方面內容：網絡中各節點的坐標信息，各節點的可行方向集，轉向耗時信息，路途耗時信息，道路實時信息 （如某時段某路段限行）。實際操作時將節點的可行方向集和道路實時信息相結合起來考慮。

定義節點s的可行方向集s’為從節點庫所s出發可以到達的庫所的集合。因本文針對雙向通行交通網絡，所以s’可理解為與s相連通的所有節點的集合。規定托肯在起始庫所的 “轉向耗時”時長為0，即不進行轉向耗時，根據可執行的變遷直接進入路途耗時。后面簡稱 “路途耗時”為 “路耗”、“轉向耗時”為 “轉耗”。

2.3 算法步驟

輸入：起始節點S，目標節點D，極限距離M

輸出：S到D的最優路徑序列

步驟1 根據1.3小節限定橢圓區域的思想，計算｜SN｜＋ ｜DN｜≤M ，得到落在橢圓區域內的庫所集合R。

步驟2 ①狀態的托肯進入起始庫所S，S存入集合A。

步驟3 在有①狀態托肯的庫所處，根據1.3小節中規則1和規則2確定可能實施的變遷集T。若-t∈T，且tR，則t不使能，T中其余變遷均使能。

步驟4 托肯根據使能的變遷數目進行衍生，新生成托肯的數目等于使能的變遷數目。查看數據庫信息，各新托肯代表各自不同的路徑進行相應的 “轉耗”和 “路耗”。

步驟5 托肯 “路耗”結束，并且此刻其相應的輸出庫所oA，則托肯進入輸出庫所o。

步驟6 判斷o是否為目標節點D，若是，表示最優路徑搜索成功，輸出到達D的托肯所途經的庫所序列，程序運行結束；若非，則先判斷o是否為其余托肯的待輸出庫所，若是，則其耗時終止并移出網絡，返回步驟3。

如圖4所示為智能算法中托肯的狀態變化流程圖。

2.4 算例

以圖3所示的交通網絡為例，經過27個單位時間可以求得從a到i的最優路徑。篇幅所限，本文只詳述搜索過程中的以下6個代表時刻，具體如下：

（1）第0時刻，初始托肯進入a，a存入集合A。a’＝｛b，d，s，u｝，根據規則，這些變遷均使能。查看數據庫確定各路耗時長，托肯準備進行各路耗。A＝ ｛a （0）｝。

（2）第6時刻，路徑ab（后面簡稱ab）的托肯在 “a→b的路耗中”；ad的托肯 “a→d的路耗完成”，d存入A，d’＝ ｛a，e，g，v｝R，因a∈A，所以實施變遷d→e、d→g、d→v；au的托肯在 “a→u的路耗中”；as的 “路耗”在時刻5完成，s’＝ ｛a，r，t｝，因 ｛r，t｝R，a∈A，所以as方向的搜索自動終止。A＝ ｛a （0），s（5），d （6）｝，如圖5 （a）所示。

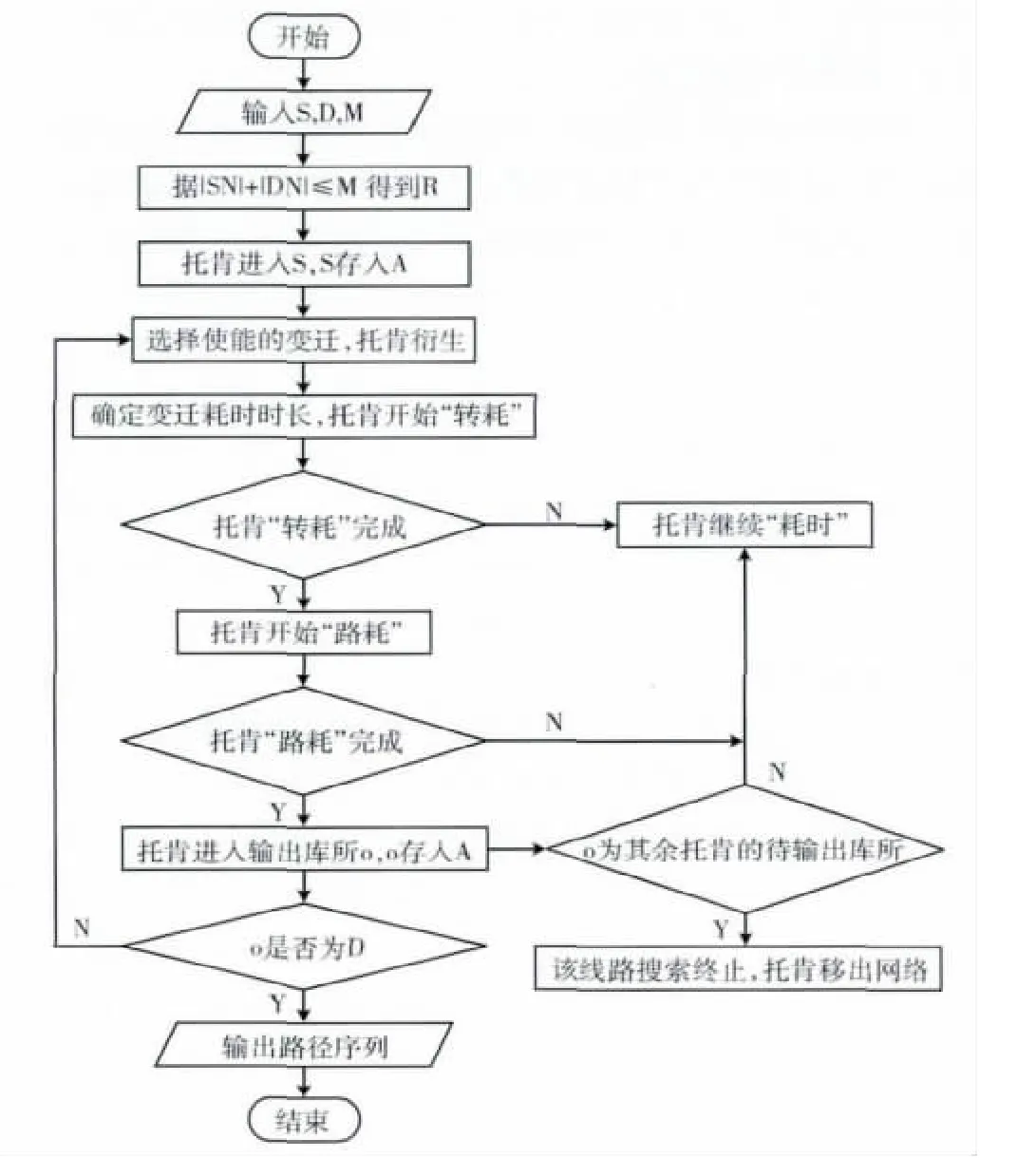
圖4 算法托肯狀態變化的流程

（3）第11時刻，ab在8時刻已路耗完成。b’＝ ｛a，c，e，r｝，因rR，a∈A，于是只執行b→c、b→e。abc的托肯 “路耗中”，abe的托肯 “轉耗完成，準備路耗”；ade的托肯 “路耗完成”，e存入A，此時abe搜索終止。e’＝｛b，d，f，h｝，｛b，d｝A，執行e→f和e→h；adg及adv的托肯 “路耗中”；u在9時刻進入A，auv的托肯 “路耗中”。A＝ ｛a （0），s （5），d （6），b （8），u （9），e （11）｝，如圖5 （b）所示。

（4）第14時刻，adeh的托肯 “轉耗完成，開始路耗”；adef、adg、adv、auv及abc的托肯均 “路耗中”。此時A＝ ｛a （0），s （5），d （6），b （8），u （9），e （11）｝，如圖5（c）所示。

（5）第20時刻，adg的g和adv的v均在時刻15擁有了托肯。考慮路徑adg，g’＝ ｛d，h，j，w｝，jR，wR，d∈A，只執行g→h；v’＝ ｛d，u，w｝，wR，｛d，u｝A，adv方向的搜索終止；adeh的托肯 “路耗完成”，此時adgh方向的搜索終止，h’＝ ｛e，g，i，k｝，｛e，g｝A，實施h→i，h→k；adef的托肯在 “路耗中”；路徑abc，c’＝ ｛b，f，p，q｝，pR，qR，b∈A，只實施c→f。此時A＝ ｛a （0），s （5），d （6），b （8），u（9），e （11），g （15），v （15），c （16），h （20）｝，如圖5（d）所示。

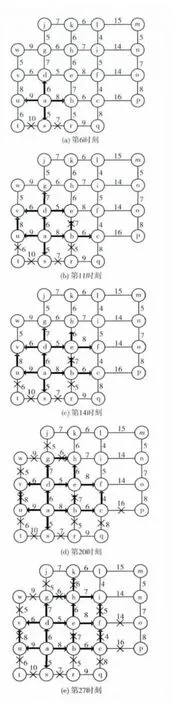
圖5 智能算法的搜索過程

（6）第27時刻，adehi的托肯率先進入目標庫所i，路徑搜索成功，輸出序列adehi，程序運行結束，如圖5（e）所示。

關于圖5中不同箭頭的說明：

本算例的結果與用改進的Dijkstra算法求得的結果一致。從以上搜索過程我們可以發現，在搜索范圍本就已經縮小很多 （限定區域）的情況下，1.2小節中托肯運行規則的定義也及時避免了很多無意義的查找，使得雙向通行網絡上復雜的路徑選擇問題變的簡單很多，極大的降低了搜索的復雜度，提高了搜索的效率。經多次反復試驗證明本智能算法是準確可用的。

3 實驗與分析

本文隨機選取北京市內4對起終點，采用P41.4GHz CPU、1GB內存的計算機進行仿真。隨著起終點間直線距離的增大，涉及路段和節點數目增多，網絡規模也越來越大，具體數據見表1。

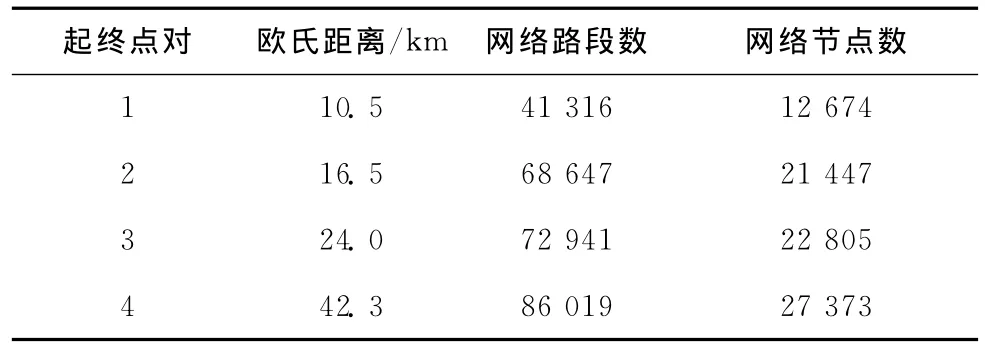
表1 用于實驗的4對起終點

對4個隨機起終點對分別用改進的Dijkstra算法，A＊算法以及本文智能算法進行路徑規劃，實驗結果見表2和圖6。

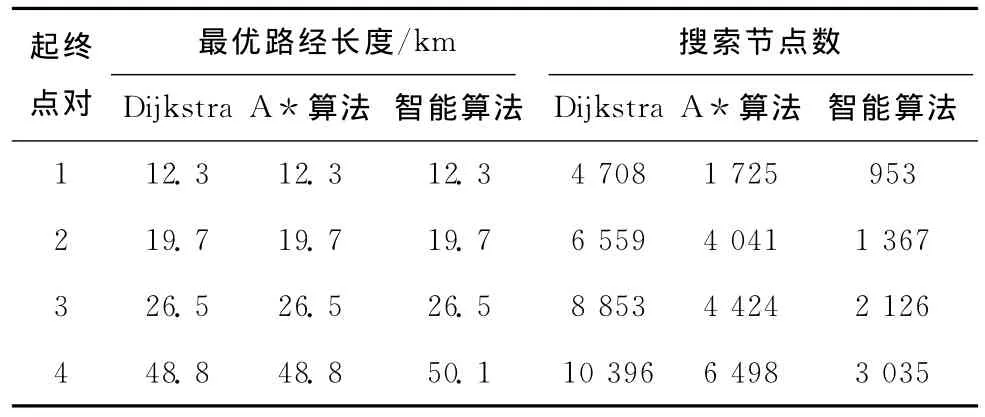
表2 3種算法路徑規劃結果

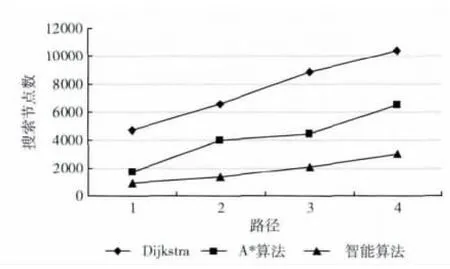
圖6 3種算法搜索節點數的比較

從試驗結果可以看出，前3個點對的起終點間直線距離相對較小 （小于40km），利用智能算法找到了最優路徑，而且搜索節點數目都明顯小于對比算法。隨著網絡規模的增大，智能算法搜索節點數變化上升的趨勢要小于對比算法。這得益于算法搜索范圍的合理限定以及路徑選擇變遷規則的定義。進一步觀察可發現，對于點對4（直線距離大于40km），智能算法求得的結果50.1稍大于對比算法的48.8，意即得到的路徑結果并非最優。這是由于在第一步設定M值時，只考慮了歐氏距離，而沒有將轉向延誤信息考慮進去，致使一些可用節點一開始就被排除到了搜索區域之外。對于歐氏距離較大的點對集來說，Dijkstra和A＊算法雖然結果更優，沒有精度損失，但是搜索范圍向四周急劇擴散，運行效率很低，而本智能算法的搜索具有一定方向性。如果為了追求結果最優而過分的增大M值會導致搜索規模的增大，從而直接影響到算法運行的效率，因此本算法實際上是一種用犧牲精度來換取效率的方法。

4 結束語

與傳統顧及轉向延誤的最優路徑算法相比，本文提出的基于Petri網的智能算法更簡便、易于實現，且運行效率較高。它面向的是最復雜的實時雙向通行網絡，并且無需對原始網絡結構做任何調整。在根據用戶需求對搜索區域進行合理的限定后，使能規則的拓展定義更有效的降低了雙向通行路網上路徑選擇的復雜度，更大程度的縮小了搜索范圍，提高了查找效率。故該算法可以為日益復雜的智能交通系統的動態交通誘導提供思路。但該算法有一個缺點是M值人為設定，這使得一些情況下的搜索結果帶有隨意性和強制性。如何更加合理的設定M值或者采用更好辦法來對搜索方向進行限定，并將其完美融合在算法中將是我們下一步要研究和探討的問題。

［1］Gutierrez E，Medaglia A L.Labeling algorithm for the shortest path problem with turn prohibitions with application to largescale road networks［J］.Annals of Operations Research，2008，157 （1）：169－182.

［2］TANG Xiaoyong，CHENG Lin，XU Shang.A least time algorithm considering delays fo intersection movements and its implementation［C］／／3rd China Annual Conference on ITS Proceedings，2007 （in Chinese）.［唐小勇，程琳，徐上.考慮轉向延誤最短路徑算法及實現 ［C］／／第三屆中國智能交通年會論文集，2007.］

［3］DU Muqing，CHENG Lin.Auction algorithm for shortest paths in road networks considering delays for intersection movements［J］.Journal of Southwest Jiaotong University，2010，45 （2）：249－254 （in Chinese）.［杜牧青，程琳.考慮交叉口轉向延誤的最短路徑拍賣算法 ［J］.西南交通大學學報，2010，45（2）：249－254.］

［4］GAO Mingxia，HE Guoguang.An arclabeling algorithm for shortest path problem considering turn penalties and prohibitions at intersections ［J］.Journal of Lanzhou Jiaotong University，2011，30 （6）：111－114 （in Chinese）.［高明霞，賀國光.考慮交叉口延誤和轉向限制的弧標號最短路徑算法 ［J］.蘭州交通大學學報，2011，30 （6）：111－114.］

［5］ZHENG Nianbo，LU Feng，DUAN Yingying.Dynamic dual graph model for turn delays on road networks ［J］.Journal of Image and Graphics，2010，15 （6）：915－920 （in Chinese）.［鄭年波，陸鋒，段瀅瀅.道路轉向延遲的動態對偶圖模型［J］.中國圖象圖形學報，2010，15 （6）：915－920.］

［6］HUANG Shengguo，SUN Tongjiang，LV Bing.Petri net simulation arithmetic of the shortest directional path in transportation net ［J］.Journal of Nanjing University of Aeronautics ＆Astronautics，2002，34 （2）：121－125 （in Chinese）.［黃圣國，孫同江，呂兵.運輸網絡的最短有向路Petri網仿真算法 ［J］.南京航空航天大學學報，2002，34 （2）：121－125.］

［7］REN Xiaolong，WEN Haoyu，LI Hua.Routing algorithm for multiple AGVs with the undirected Petri Net ［J］.Journal of Xidian University，2008，35 （3）：517－522 （in Chinese）.［任小龍，溫浩宇，李華.無向Petri網的多AGV最優路徑方法研究 ［J］.西安電子科技大學學報，2008，35 （3）：517－522.］

［8］WU Zhehui.Petri net introduction ［M］.Beijing：Machine Press，2006 （in Chinese）.［吳哲輝.Petri網導論 ［M］.北京：機械工業出版社，2006.］

［9］WANG Haimei，ZHOU Xianzhong.Improved shortest path algorithm for restricted searching area ［J］.Journal of Nanjing University of Science and Technology（Natural Science），2009，33 （5）：638－641 （in Chinese）.［王海梅，周獻中.一種限制搜索區域的最短路徑改進算法 ［J］.南京理工大學學報，2009，33 （5）：638－641.］

［10］LI Shuju.The modeling of variable transportation network and the shortest path algorithm based on petri net ［D］.Guangxi：Guangxi Teachers Education University，2012 （in Chinese）.［李書舉.基于Petri網的變數交通網絡建模及其最短路徑算法研究 ［D］.廣西：廣西師范學院，2012.］