改進遺傳算法求解作業車間提前/拖期調度問題

葛安華，周晏明，李權章

(東北林業大學工程技術學院，哈爾濱 150040)

作業車間調度問題，是一類滿足任務配置和順序約束要求的資源分配問題，其目的是對作業進行有效排序，是最難解決的組合優化問題之一［1］。在實際的制造企業加工車間中所面臨的問題大多為作業車間調度，如車間生產自動化水平相對較低，憑計劃員經驗調度，頻繁調整生產計劃，設備利用率不均衡，生產周期加長以及人員與設備的浪費［2］。對作業車間調度問題的研究有助于提高生產車間自動化水平，改善設備利用的均衡性，具有重要理論意義和工程價值。

隨著近年來智能優化技術的發展，許多求解作業車間調度問題的啟發式方法被提出，如禁忌搜索算法、模擬退火算法、遺傳算法等，國內外的專家學者在相關方面也做了大量的研究工作［3－5］。文獻［3］研究了一種基于禁忌搜索技術解決作業車間調度最短完工時間的算法。禁忌搜索算法偏向于局部搜索，對初始解的依賴性較強，不好的初始解會造成計算時間過長。文獻 ［4］闡述了模擬退火算法在作業車間調度問題上的應用。雖然理論上模擬退火算法可以在足夠長的時間后跳出局部最優，但在實際應用中往往會陷入到優化效果與計算時間的矛盾中。遺傳算法，因其通用性強，全局搜索性能較好，在求解過程中可同時保留多個方案而得到廣泛的應用。但因其固有特征，在求解作業車間調度問題時仍具有局部尋優能力差，搜索效率不高等現象。文獻 ［5］通過改進遺傳算法的編碼方式、交叉、變異策略等方法提高了算法求解總加工時間最短的作業調度問題的能力。

在實際的車間調度問題中，企業的生產調度多以產品的訂單交貨期為主要依據［6］，故本文將最小化產品的提前/拖期懲罰作為目標函數，以提高遺傳算法在作業車間調度問題中的求解質量和收斂速度為目標，提出一種帶有記憶功能的改進遺傳算法，并利用爬山算法提高其局部搜索能力，通過與其他算法計算結果的對比分析驗證其優越性。

1 問題描述

作業車間提前/拖期調度問題可以描述為:

(1)在m臺機器上生產n個相互獨立的產品，產品集合表示為N={1，2，……，n}，機器集合表示為M={1，2，……，m}，每個產品需經過若干道工序才能完成，且每道工序在特定的機器上加工;

(2)sijk和tijk分別表示第i個產品的第j道工序在機器k上的開始加工時間和加工時數，產品i的最后一道工序的開始加工時間和所需加工時數分別是siek和tiek，則產品i的完工時間ci=siek+tiek;

(3)產品i的交貨時間窗口為 ［ei，di］，產品i單位時間的提前懲罰為ωi，拖期懲罰為αi，若產品在時間窗口之內完成生產，則不受懲罰，否則對產品i進行懲罰;

目標函數為最小化產品的總懲罰，表示為:

公式 (1)表示的是目標函數，即最小化所有產品的提前/拖期懲罰。公式 (2)表示工藝約束條件決定的各產品的各道工序的先后加工順序以及各道工序在相應機器上的加工順序。其中，若機器h先于機器k加工產品i，則aihk為1否則為0，若產品i先于工件j在機器k上加工，則bijk為1否則為0;sik和tik分別表示產品i在機器k上的開始加工時間和加工時數;G是一個足夠大的正數。

2 遺傳算法的設計

為提高遺傳算法的收斂速度，采用一種可以保留較高適應度個體的記憶功能，并利用爬山算法對記憶種群進行局部搜索，從而增強算法的局部搜索能力。改進遺傳算法的具體步驟如下:

(1)設置種群尺寸為PS，記憶庫尺寸為MS。

(2)產生初始種群P(t)，從初始種群中選取MS個較優個體保存在記憶庫M(t)中。

(3)分別以交叉概率Pc和變異概率Pm對個體進行交叉和變異操作，將得到的子代個體保存到種群O(t)中。

(4)以記憶庫M(t)中的染色體為初始解，利用爬山算法進行局部搜索，得到更新后的記憶庫M’(t)。

(5)評價種群P(t)，O(t)和M’(t)，從中選擇出種群P(t+1)。

(6)進行記憶庫的第二次更新，從種群P(t+1)中選取其中較優的MS個個體更新記憶庫。

(7)如果滿足終止條件 (達到最大迭代次數N)則結束計算，否則轉向 (3)。

2.1 編碼設計

遺傳算法在進行編碼時，必須要考慮染色體的合法性、有效性、冗余性以及表征解空間的完全性［7］。編碼設計的優劣對算法的各子階段都有重大影響。好的編碼設計可以保證在交叉、變異后依然保持染色體的有效性和完全性。目前已提出的編碼方法有，基于優先規則的表達法、基于工序的表達法、基于優先表的表達法、基于工件的表達法、基于工件對關系的表達法、基于機器的表達法等［8］。

將基于工序表達法與機器表達法的實數編碼方法相結合，形成一種新的雙染色體矩陣編碼方式。對于m臺機器生產n種產品的問題，基于工序表達的實數編碼，染色體有n×m個基因，每個代表產品的十進制數都在基因中重復出現m次，工序調度的順序由染色體基因的順序決定;同樣基于機器表達的實數編碼，其染色體也有n×m個基因，每個染色體基因分別表示相應產品的各道加工工序所在的機器編號。

2.2 種群的初始化及適應度函數的確定

依據上述編碼方式的種群初始化很簡便，首先建立一個隨機分配個體基因的循環，生成個體的第一行基因，再利用產品的工序順序約束生成個體的第二行基因。如此重復進行，直至達到設定的種群規模。

根據目標函數定義的適應度函數如下所示:

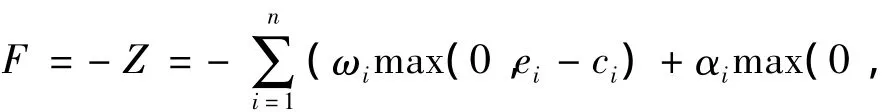
式中:F為適應度函數，F取值越大，總懲罰越小，其對應調度方案的適應度越高。

2.3 遺傳算子

2.3.1 復制

2.3.2 交叉

考慮到基于雙染色體矩陣編碼交叉后子代的調度可行性，基于部分映射雜交 (PMX)和染色體分離的思想提出一種部分映射交叉重排算子［9－10］。這種交叉方法的具體過程如下:

(1)分別在兩個父代染色體上選擇兩個步數相同的交叉點。

(2)兩個父代交換彼此交叉點之間的子串。

(3)確定被交換的子串間基因的映射關系。

(4)消除掉染色體中多余的基因，以相應的缺失基因補充。

(5)根據產品相應工序所需加工機器的約束，重新排列染色體中的第二行基因。舉例說明部分映射交叉重排算子，如圖1所示，A、B為兩個父代染色體，經交叉后得到兩個子代個體A’、B’。

2.3.3 變異

為保證變異后的個體仍為可行解，基于前面交叉算子的設計思想，采用互反變異重排方法進行個體的變異操作。首先在染色體上隨機選擇兩個位置，然后交換這兩處的基因，再根據產品各工序所需加工機器的約束重排第二行的染色體基因［11］。

圖1 交叉算子Fig.1 Crossover operator

2.4 爬山操作

爬山算法，又稱局部搜索算法，是一種基于鄰域搜索技術的、沿著可能改進解的質量的方向進行單方向搜索 (爬山)的搜索方法，其局部搜索能力很強，是一種常用的尋找局部最優解的方法［12］。它在解的空間內，以當前節點為中心和其鄰域的節點值相比較，若其鄰域節點更優，則用其替換當前節點繼續搜索;反之則返回當前節點繼續搜索。如此循環直至到達終止條件。

為彌補傳統遺傳算法局部搜索能力較弱的不足，采用基因逆轉算子來實現爬山操作，更新種群記憶庫。具體步驟如下:

(1)對于記憶庫中的每個個體，隨機選擇個體上的兩個點，再將兩點之間的元素逆序插回到原來的位置中。

(2)判斷逆轉后的個體適應值是否增加，若增加則以逆轉后的個體替換原個體，否則仍保留原個體。

(3)重復 (1)、(2)的操作，直至達到設定的迭代次數為止。

3 仿真實驗

本節的仿真實驗在Genuine Intel(R)T2130 1.87GHz處理器，2.0GB RAM，MATLAB R2011a環境下進行。

3.1 仿真分析

為驗證文中改進遺傳算法的優越性，將本文算法與文獻［2］中的遺傳算法 (IGA)進行比較。取種群規模100，記憶庫規模20，交叉概率0.5，變異概率0.05，在不同規模 (n×m)下進行實驗對比。實驗中生產機器的集合，各工序所需加工時間隨機產生，且滿足平均分布。由于篇幅有限在此僅列出6組實驗結果，見表1，每種規模仿真實驗20次，其中最優值為所有運算結果中目標函數最小的值，平均值為每次運行所得最優值的平均值。

表1 方法比較Tab.1 Method comparison

從表1中可以看出，本文算法所求得的最優值和平均值均優于IGA，而且隨著規模的不斷擴大，效果更加明顯，體現了本文算法的優越性。

3.2 實例應用

以某加工制造企業為例，驗證本文算法在實際應用中的可行性和有效性，設提前懲罰為0.8，拖期懲罰設為1.4，產品各生產工序所需的加工時間、加工機器以及各產品的交貨時間窗口見表2。

表2 加工數據Tab.2 Machining data

設定遺傳算法的參數為:交叉概率Pc=0.4，變異概率Pm=0.02，種群尺寸PS=100，記憶庫尺寸MS=20，最大迭代次數N=100，爬山算法的最大迭代次數N’=5。分別采用不帶記憶功能的普通遺傳算法和文中的改進算法，進行20次仿真實驗，兩種算法的實驗結果見表3，圖2為兩種算法的收斂情況比較。

表3 實驗結果Tab.3 Experimental results

圖2 兩種算法收斂情況Fig.2 Convergence situation of the two algorithms

從表3中可以看出，本文算法求解出了問題的最優解0，在20次仿真中搜索到最優解的次數為18次，而且搜索到最優值的平均迭代次數和平均計算時間都要優于普通遺傳算法，說明改進遺傳算法的運算性能穩定，搜索能力強。通過圖2的比較則可以進一步看出，在整個搜索過程中，本文算法的收斂速度較快，在41代左右達到全局最優解0，而普通遺傳算法的收斂速度明顯較慢，且在43代左右以后逐步陷入局部最優。綜上所述可知，無論是在求解質量還是收斂速度上，文中的改進遺傳算法都優于不帶記憶功能的普通遺傳算法。

仿真結果表明，通過本文算法可以求解出懲罰值為0的最佳調度方案，即所有產品均可在交貨窗口內按時完成生產。求解出的最優個體如下:

4 結論

為求解作業車間提前/拖期調度問題，文中提出一種基于雙染色體矩陣編碼的改進遺傳算法，并利用記憶庫和爬山算法提升算法的尋優能力和搜索速度。改進遺傳算法的編碼簡潔、直觀，收斂性能好，并能較好地解決相關的車間調度問題，滿足大規模此類調度問題的需要。下一步將繼續研究結合其他啟發式方法的改進遺傳算法在多目標作業車間調度問題中的應用，并進一步提高算法的性能。

【參 考 文 獻】

［1］王萬良，吳啟迪．生產調度智能算法及其應用［M］．北京:科學出版社，2007．

［2］蘇 瑩，李 杰，陰慧輝，等．改進遺傳算法求解作業車間調度問題［J］．制造技術與機床，2010，10:104 －108．

［3］黃 志，黃文奇．一種基于禁忌搜索的作業車間調度算法［J］．計算機工程與應用，2006，03:12 －14．

［4］趙良輝，鄧飛其．用于作業車間調度的模擬退火算法［J］．制造業自動化，2006，28(3):10 －23．

［5］蘇 春，王大俠．基于改進遺傳算法的偏柔性作業車間調度［J］．工業工程，2010，13(6):61 －65．

［6］陳 杰，張力菠．供應鏈環境中交貨期問題的研究［J］．中國制造業信息化，2005，34(4):105 －107．

［7］潘全科，朱劍英．多工藝路線的作業車間模糊調度優化［J］．中國機械工程，2004，15(24):2199 －2202．

［8］呂文閣，劉志勇，成思源，等．基于競選算法的生產調度問題的研究［J］．機床與液壓，2009，37(10):33 －36．

［9］玄光男，程潤偉．遺傳算法與工程優化［M］．北京:清華大學出版社，2004．

［10］韓冰源，肖生苓．配送中心線路優化方法的探討［J］．森林工程，2005，21(2):67 －68．

［11］郎茂祥．配送車輛優化調度模型與算法［M］．北京:電子工業出版社，2009．

［12］郎茂祥，胡思繼．用混合遺傳算法求解物流配送優化問題的研究［J］．中國管理科學，2002，10(5):51 －56．