計及風力發電并網的配電網潮流優化

程站立，胡 枚，陳世雯

(安徽省電力公司馬鞍山供電公司，安徽 馬鞍山 243000)

0 引言

隨著全球資源環境壓力的不斷增大，社會對環境保護、節能減排和可持續性發展的要求日益提高。同時，電力市場化進程的不斷推進以及用戶對電能可靠性和質量要求的不斷提升，要求未來的電網必須能夠提供更加安全、可靠、清潔、優質的電力供應，而具有靈活、清潔、安全、經濟、友好等性能的支持各種分布式電源(微型燃氣輪機、燃料電池、太陽能光伏發電、風力發電等)以“即插即用”的方式友好接入的智能電網就成了未來電網的發展方向［1］。

分布式電源(distributed generation，DG)是指在配電系統靠近用戶側引入的功率為數千瓦至50 MW的小型模塊式、與環境兼容的獨立電源。分布式發電具有投資少、占地小、建設周期短、節能、環保等特點。風電是具有可再生性的分布式電源，近年來隨著中國能源結構的調整，風電日益得到重視，并制訂了有關政策支持風電的快速發展，風電已成為分布式發電中發展最快的、最具有發展前景的一種發電方式［2］。

風電并入配電網對配電系統的網損和電壓分布有重要的影響，而潮流計算是對其進行量化分析的主要手段。文獻［3］在建立PQ模型時根據有功功率調整無功功率，在有功功率已知的情況下，根據有功功率與無功功率的近似解析式求得風場無功功率，然后進行計算。文獻［4］在分析風電機的潮流模型的基礎上，提出了RX模型，此模型充分考慮到了風力發電機的輸出功率特性，在常規潮流迭代基礎上增加了異步發電機的滑差迭代計算。但是該方法潮流方程維數較大，計算程序復雜。文獻［5］利用蒙特卡羅方法仿真模擬風機風速，建立了包含風力發電機組的配電網無功優化模型，并采用靜止無功補償設備對配電網進行無功補償。在分析風電機組潮流計算中常用的幾種數學模型的基礎上，采用了前推回帶法計算了計及風力發電的配電網潮流，在潮流計算中考慮使用并聯電容器對電網進行無功補償，并建立了以全網的有功網損最小為目標函數的無功優化模型，并通過算例分析對所提的方法進行了仿真驗證。

1 風力發電機組模型分析

1.1 風電機組的PQ等值模型

風電機組主要由風力機和異步發電機等主要元件組成［4］。在穩態情況下，風力機從風能中吸收的機械功率與風速的三次方成正比即

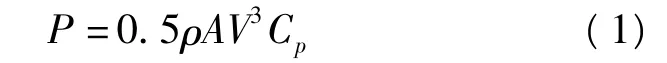
式中，r為空氣密度，kg/m3;V為風速，m/s;A為風力機的掃掠面積，m2;Cp為風力機的風能利用系數，表明風輪機從風中獲得的有用風能的比例，它是葉尖速比λ的函數，且有λ=ωr/v;r為風輪半徑;ω為風輪角速度。

在電力系統潮流計算中的風電機組傳統的處理方法是將其等值為PQ節點，并認為風電機組中電容器自動分組投切，以保持風電場的功率因數保持不變，即有

式中，θ是并網風電場的功率因數角。由于采用的是異步發電機，所以θ一般位于第四象限，tanθ為負。

1.2 風電機組的RX等值模型

在含風電機組的潮流計算中，RX等值模型基本思想是基于兩個迭代過程，一是通過常規潮流迭代過程計算異步發電機的機端電壓;二是通過異步發電機滑差的迭代過程計算異步發電機的滑差。根據能量守恒定律，風力機吸收的機械功率和異步發電機發出的電氣功率理論上應該相等。因此，當異步風力發電機的電氣功率與風力機吸收的機械功率的差值達到允許的誤差范圍時，說明風力發電機組達到穩定運行點。這種等值模型要基于以下兩個假設［6］。

(1)在滑差s已知的情況下，電機在穩態情況下可以模擬等效成一個阻抗。

(2)風速和功率因數曲線在已知的情況下可以求出滑差的數值大小。

由異步發電機組等值電路原理圖1可知，在RX等值模型中，其等值阻抗為

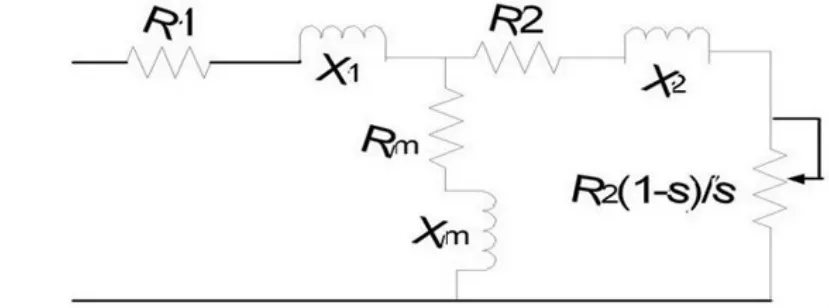
圖1 異步發電機等值電路［4］

圖1中，X1為定子漏抗;X2是轉子漏抗;Xm是異步發電機的激磁電抗;R1是定子電阻;R2是轉子電阻;Rm是勵磁電阻;s為轉差。

異步發電機組發出的有功功率P與轉子電流I2，異步發電機的滑差s之間的關系為

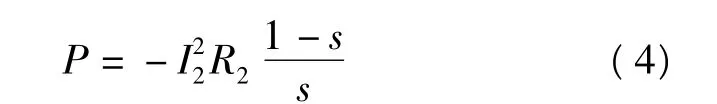
采用RX等值模型方法能夠較好地反映異步電機的特性，但由于需要兩個迭代過程，其總的迭代次數多，計算負擔重，同時收斂性變差。

1.3 風電機組的穩態等值模型及簡化模型

目前，風力發電的機組一般都是異步發電機組。異步發電機在超同步運行的情況下以發電方式運行。它吸收風力機提供的機械能，發出有功功率。但是異步發電機本身無勵磁裝置，需要從電網或者電容器中吸收無功功率提供其建立磁場所需的勵磁電流。多臺風力機組按照一定規則排列構成風電場，風電場的功率為所有風電機組輸出功率之和［7］。

由圖1中的電路關系可知發電機的有功功率的表達式為

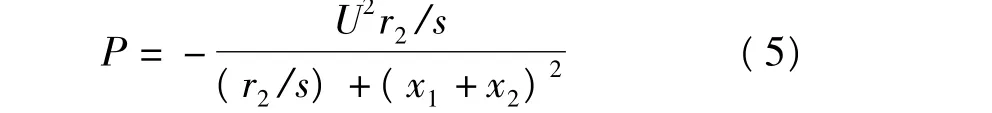
在不考慮并聯電容器的情況下，發電機從電網中吸收的無功功率Q為

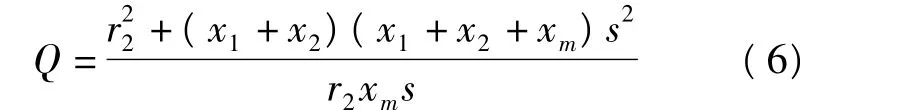
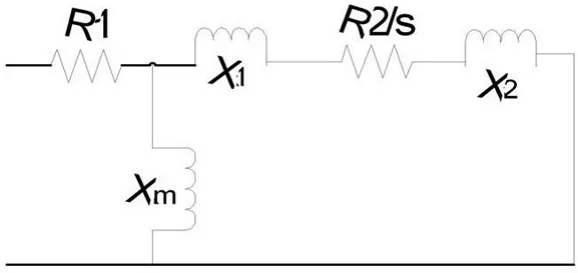
圖2 異步發電機簡化模型

在圖1中，Xm＞＞X1且定子電阻和鐵心的功率損耗與有功功率相比可忽略，因此，可以將勵磁支路移至電路首端，得到簡化的異步發電機Γ型等值電路，如圖2所示。

若假設風電場的有功功率為風機的機械功率，可由電路連接關系得出風電機組無功功率的表達式。經過簡化則式(6)可變為式(7)，如下。

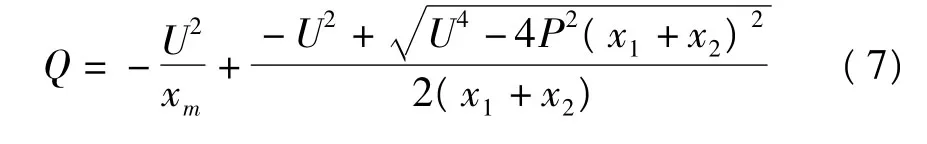
為了減少網絡損耗，通常與風力發電機組并聯安裝電容器組。電容器組自動分組投切，以保證風力發電機組的功率因數在允許的范圍內變動。帶并聯電容器組的風力發電機組的功率因數為［8］

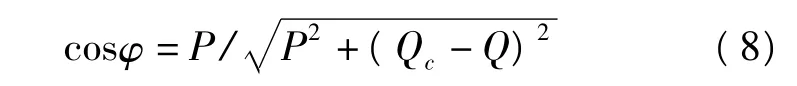
式中，P為風力發電機輸出的有功功率;Q為風力發電機吸收的無功功率;Qc為并聯電容器輸出的無功補償容量，可以表示為

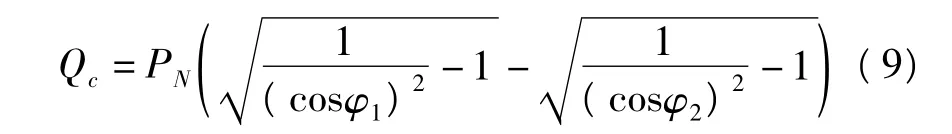
式中，cosφ1為發電機的初始功率因數;cosφ2為并聯電容器組后的發電機功率因數。

并聯電容器組的實際投入組數為

式中，［n］表示對分數取整數運算;QN為并聯電容器的單位容量。考慮并聯電容器組輸出無功與電壓幅值有關，風機從電網吸收的實際無功為

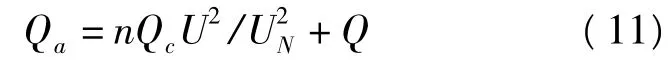
在潮流計算中根據每次得到的電壓幅值由式(7)計算其吸收的無功，再根據要求達到的功率因數由式(9)和式(10)求出并聯電容器的組數，最后由式(11)得到實際吸收的無功，這樣就可以在下次潮流計算時把風機并網節點作為PQ節點進行潮流計算［3］。

2 改進的粒子群算法

由于基本粒子群算法過多的依賴于個體最優解和種群最優解的信息，搜索區域可能因此會受到限制，而且設置參數、種群的大小以及它們之間的關系也沒有可供參考的準則，因此算法有開始效果好，接近最優解時收斂很慢等缺點。針對不同的優化問題，在基本粒子群優化算法基礎上的許多改進己經提出并產生出一些新的粒子群優化算法模型［9］。

為保證算法的收斂性，ClERC提出了對PSO進行改進的收縮因子方法 (constriction factor method，CFM)。由于該方法定義了一個收縮因子K，所以該改進的PSO算法被稱為PSO-cf，其定義如下。

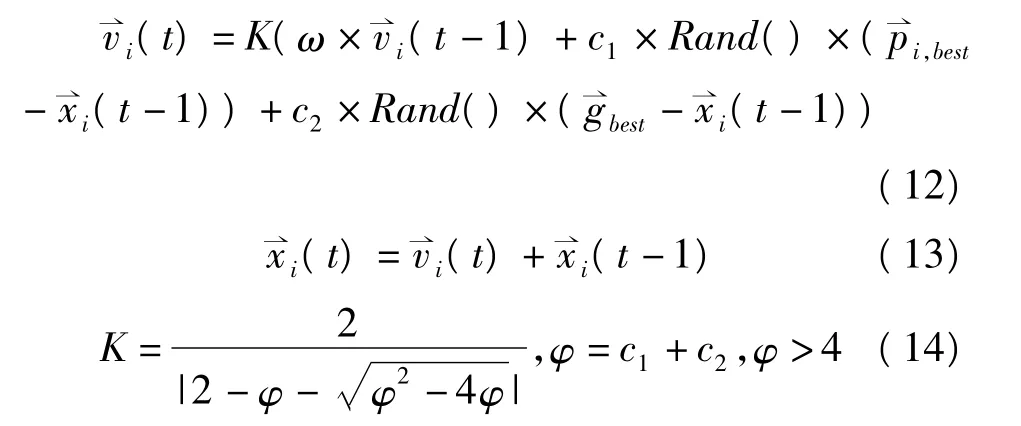
式中，K是收縮因子;ω是慣性權值;c1和c2分別是加速常數;(t)是第i個粒子的位置;(t)是第i

這里將系統有功功率損耗和節點電壓偏差最小作為目標函數，并采用罰因子的方式將多目標的無功優化模型轉變成單目標的優化問題。具體目標函數如下。

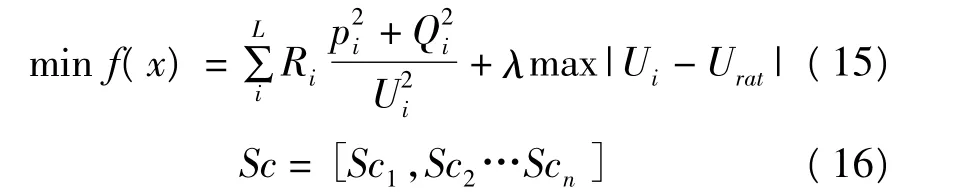
式(15)中，Ri是支路電阻;Pi和Qi分別是支路的有功功率和無功功率;Ui是節點i上的電壓幅值;Urat是節點參考電壓(標幺值)取值為1.0 p.u.;λ是罰因子，這里取值為10。式(16)中，Sc1是補償電容器的投切組數。

3 基于改進粒子群算法的配電網潮流優化步驟

前推回帶法具有編程簡單、計算效率高、且隨著網絡復雜程度的增加速度降低不大、收斂特性好等優點，特別適用于計算輻射型電網結構的潮流，是一種性能優異的配電網潮流算法［10］。因此這里擬采用此方法進行系統潮流計算。

進行潮流計算前，需要給定的初始量有風電場節點電壓幅值、風力發電機的風速、定子和轉子電抗、勵磁電抗、并聯電容器組的額定電壓、并聯電容器組額定電壓下的單位容量以及進行無功補償的并聯電容器的投切百分比。具體的潮流計算過程如下。

①確定風機輸出的有功功率，輸入系統數據并初始化粒子種群;②由式(7)～式(11)計算風電場電容器組的安裝組數以及初始時刻風力發電機吸收的無功功率和并聯電容器組發出的無功功率;③調用前推回推潮流計算程序計算目標函數值，即分別計算群體中的每個粒子的潮流，得到每組控制變量下的有功損耗;④記錄粒子當前的個體極值pbesti及目標函數值f(pbesti)，從pbesti中確定整體極值gbest并記錄gbest對應的目標函數值;⑤更新粒子飛行速度以及在解空間中的位置;⑥再次調用前推回推法計算系統潮流，重新判斷各個粒子的目標函數值，如果f(pbesti+1)＜ f(pbesti)則更新pbesti，否則不更新;將每個粒子的適應值與整個粒子群的gbest相比較，如果較好則重新設置gbest，否則gbest值不變，重新初始化粒子群;⑦當滿足全局最好位置連續若干次無變化或達到預先給定的最大迭代次數條件后，迭代停止，否則轉入步驟(3);⑧輸出補償電容器的投切組數以及對應的網損值，潮流優化結束。

4 算例分析

采用圖3所示的33母線配電系統進行分析。根據文獻［10］，系統電壓基準值為12.66 kV，視在功率基準值為10000 kV·A，系統總的有功負荷是3715.0 kW，總無功負荷是2300.0 kW。在節點17、24、32并入3臺風機，單臺風力發電機的額定容量為600 kW，其額定電壓為0.69 kV，功率因數為0.89。在節點9、16、30并聯3組補償電容器，并聯電容器組的額定電壓為0.69 kV，每臺并聯電容器的額定容量為40 kvar，采用百分比值確定容量，調節精度為0.01。風電場的功率因數由初始的0.89提高到0.99。并聯風機的參數參考文獻［11］。潮流計算方法采用前推回帶法。

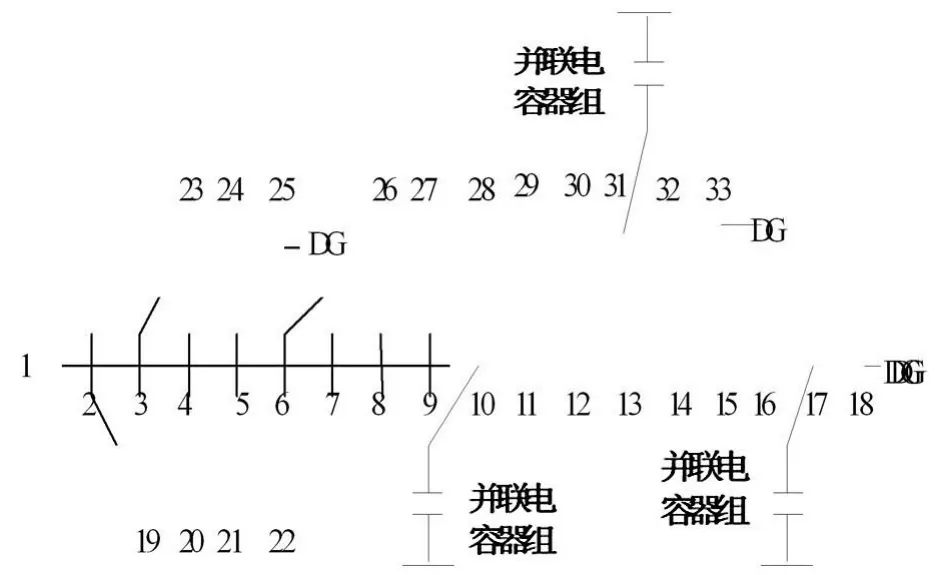
圖3 33母線測試系統

由于33母線系統是三相平衡系統，因此在潮流計算過程中只算其一相即可。風機并入前的33母線系統的節點電壓幅值如圖4所示。

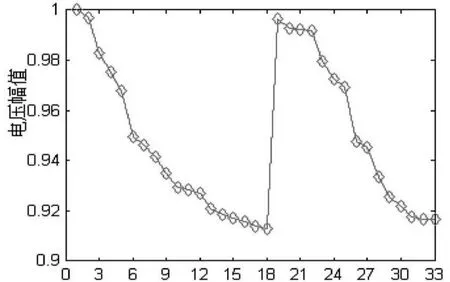
圖4 33母線系統節點電壓幅值

由圖4可以看出33母線系統的電壓幅值在0.91～1.0 p.u.之間。潮流計算經過5次迭代后收斂，系統總的有功網損為405 kW。

在節點24、32、17并入風電機組后，潮流計算經過5次迭代收斂，迭代結束后的節點電壓幅值與風機并網前比較如圖5所示。

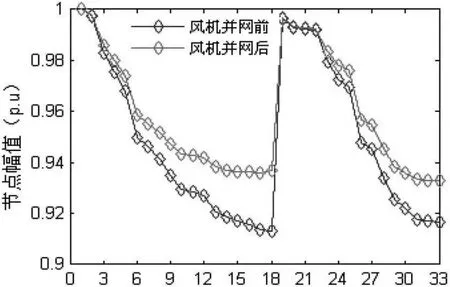
圖5 含風電機組的系統電壓幅值

由圖5可以看出風機并網后向系統發出有功功率，供給與風電場節點相近的節點負荷，有效地提高了整個配電網的電壓幅值水平，節點電壓幅值范圍為0.932～1.0 p.u.之間。潮流計算結束后得到系統有功網損為229 kW。

在節點9、16、30接入并聯電容補償器組后，應用改進的粒子群算法對配電網進行無功優化，試驗次數為20次，種群規模為39，維數為3，收縮因子為0.7298，加速因子均為2.01，迭代收斂精度為10-6，控制變量范圍為0～5。經過優化后的電壓幅值與優化前相比較如圖6所示。

采用改進粒子群算法的配電網潮流優化程序經過5次迭代后收斂，節點電壓幅值為0.935～1.0 p.u.，優化補償后的系統有功網損為195 kW，優化后的電容器的無功補償容量分別為 23 kvar、30 kvar、40 kvar。相比沒有優化的含風機的配電網，電壓幅值有了進一步的提高，系統總的有功網損也有了顯著的降低。采用改進的粒子群算法對含風機的配電網進行潮流優化不但沒有增加潮流收斂需要的迭代次數，而且有效地降低了系統的有功網損，提高了節點電壓幅值。證明所使用的潮流優化方法是正確的。

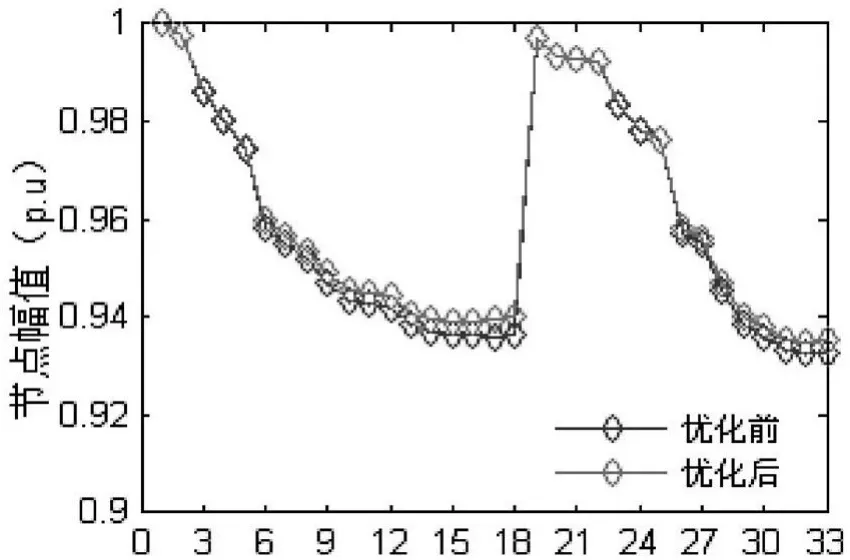
圖6 優化后的系統電壓幅值

5 結論

研究了計及風機并網的配電網潮流優化方法，通過比較分析風電場并網潮流計算的幾種常用模型，選用帶補償電容的風機穩態等值模型作為研究對象，并采用改進的粒子群算法對風機并網的配電網潮流進行了優化。仿真實驗結果表明，該算法可行，對于減少網絡的功率損耗和提高節點電壓幅值有顯著的作用，為各種DG的并網優化運行提供了理論和方法參考。

［1］陳述勇，宋書芬，李蘭欣，等.智能電網技術綜述［J］.電網技術，2009，33(8):1-7.

［2］雷亞洲.與風電并網相關的研究課題［J］.電力系統自動化，2003，27(8):84-89.

［3］李新，彭怡，趙晶晶，等.分布式電源并網的潮流計算［J］.電力系統保護與控制，2009，37(17):78-81，87.

［4］徐嬌，李興源.異步發電機組的簡化RX模型及潮流計算［J］.電力系統自動化，2008，32(1):22-25.

［5］陳琳，鐘金，倪以信，等.含分布式發電的配電網無功優化［J］.中國電機工程學報，2006，30(14):20-24.

［6］劉洋，康凱，王邦惠，等.含風電系統的潮流計算分析［J］.山東電力技術，2009(4):21-24.

［7］胡敏，周任軍，楊洪明，等.考慮風力發電的系統無功優化模型和算法［J］.長沙理工大學學報:自然科學版，2009，6(1):43-48.

［8］王守相，江興月，王成山.含風力發電機組的配電網潮流計算［J］.電網技術，2006，30(21):42-45，61.

［9］劉述奎.基于自適應聚焦粒子群算法的電力系統無功優化［D］.成都:西南交通大學，2009.

［10］王守相，王成山.現代配電系統分析［M］.北京:高等教育出版社，2007.

［11］顧威，李興源，魏巍.異步發電機穩態模型研究［J］.四川電力技術，2009，32(3):20-24.