面向多種調度模式的電力交易計劃統一編制與管理

許立雄，李 響，劉友波，劉俊勇，凌 亮，孫 毅

(1.四川大學電氣信息學院，四川 成都 610065;2.四川省電力公司，四川 成都 610041)

0 引言

交易計劃編制工作是電力交易中心的主要工作之一，其結果將直接影響后續調度中心的工作［1］。交易計劃按照時間跨度可以分為短期的日交易計劃、中期的月度交易計劃和長期的年度交易計劃。短期的日交易計劃國內外研究得比較成熟［2-6］，長期的年度交易計劃國內外的研究成果也比較豐富［7-10］，而對于中期的月度交易計劃的研究相對還比較匱乏。文獻［11］基于“三公”調度模式，建立了全周期變時段發電計劃優化模型。然而“三公”調度模式不能有效地引導電力工業朝著提高能源使用效率，減少環境污染的方向實現可持續發展，因此國務院特別頒布了《節能發電調度辦法》。文獻［1］提出在節能調度模式下的一種綜合耗量優化方法，綜合考慮了發電企業、電網公司和社會環境三方利益，用于解決省級電網直調火力發電單元月度電能交易計劃編制問題。上述文獻均是針對某一種調度模式研究月度交易計劃的編制，而目前就省一級的電力交易中心而言，月度交易計劃的編制正由平均分解的方式向節能分解的方式過渡，迫切需要能夠同時考慮多種調度方式的月度交易計劃編制方法。在深入分析平均分解和節能分解的編制模型的基礎上，提出了考慮多種調度模式的月度交易計劃統一編制模型，采用禁忌-粒子群算法進行求解，并開發了相應的系統實現月度交易計劃的編制與管理。

1 月度交易計劃編制模型

月度交易計劃編制是根據未來月份系統的電力電量需求，各個發電機組的檢修安排、啟停限制、發電量限制等條件，確定各個發電機組在未來月份的開停、出力及電量。編制完的計劃還需要滿足相應的要求，如能耗最小、各個發電機組年合同電量完成進度相當等。這種要求與不同的調度模式相對應，如能耗最小是節能調度模式下的要求;而各個發電機組年合同電量完成進度相當則是“三公”調度模式下的要求。

將編制完的計劃需要滿足的要求作為目標函數，系統的電力電量平衡、機組運行限制作為約束條件，建立考慮多種調度模式的月度交易計劃編制優化模型，通過設置不同的目標函數來反映不同的調度模式。模型具體描述如下。

1.1 優化目標

1)節能調度模式

節能調度模式要求按照各個發電機組的能耗由小到大安排發電，以提高電力工業能源使用效率，節約能源，促進能源和電力結構調整。因此節能調度模式下月度交易計劃編制模型的優化目標為發電能耗最小。

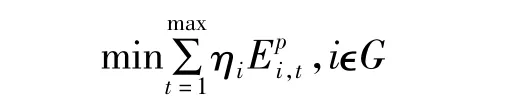
式中，ηi為發電機組i的單位能耗;為時段 t內發電機組i的計劃發電量。

2)“三公”調度模式

“三公”調度模式是中國傳統的調度模式，“三公”調度的關鍵指標是電廠年度合同電量進度，即要求各電廠的電量完成進度盡可能相近。以時段內各個發電機組年合同電量完成進度的方差來衡量各個機組之間年合同電量完成進度的偏差，則優化目標可具體描述如下。

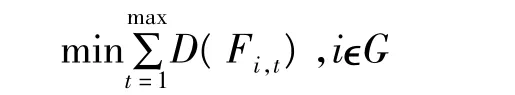
式中，D(Fi，t)為時段t內各個發電機組年度合同電量完成進度的方差;Fi，t為時段t內發電機組i的年度合同電量完成進度。

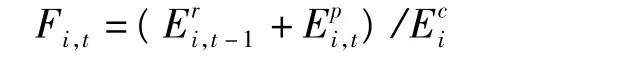
3)統一模型

采用不同調度模式進行月度交易計劃的編制，區別體現在目標上:節能調度模式以能耗最小作為計劃編制的指導;“三公”調度以各個機組年合同電量完成進度盡可能相近作為計劃編制的指導。因此，可以通過引入權重將不同的目標函數綜合來實現不同調度模式下月度交易計劃編制的統一。

統一模型下的目標函數可描述為

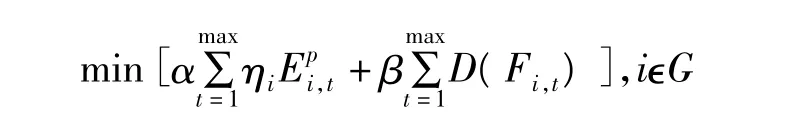
式中，α、β為權重，當α=1，β=0時，對應于節能調度模式;當α=0，β=1時，則對應于“三公”調度模式。

1.2 系統平衡約束

發電機組的出力需要滿足系統的負荷及備用需求;同時在時段內所發電量需要與負荷消耗的電量相匹配。因此系統的平衡約束包括了電力平衡約束和電量平衡約束。

1)電力需求約束

電力需求約束為

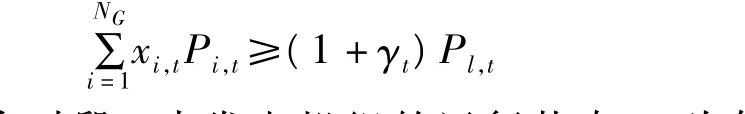
式中，xi，t為時段 t內發電機組的運行狀態，0為停機，1為運行;Pi，t為時段t內發電機組的出力;NG為發電機組總臺數;γt為時段t內系統的備用率;Pl，t為時段t內系統的總體負荷電力需求。

2)電量需求約束

電量需求約束為

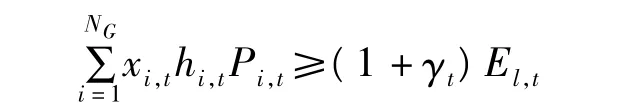
式中，xi，t為時段 t內發電機組的運行狀態，0為停機，1為運行;hi，t為時段 t內發電機組的利用小時數;Pi，t為時段t內發電機組的出力;NG為發電機組總臺數;γt為時段 t內系統的備用率;El，t為時段 t內系統的總體負荷電量需求。

1.3 機組約束

發電機組本身存在各種運行的限制，如檢修、最小啟停時間等。具體的約束描述如下。

1)機組必須停機約束

機組必須停機約束為

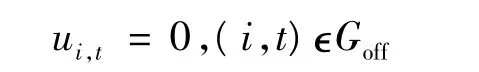
式中，Goff為時段t內由于檢修等原因必須停運的發電機組集合。

2)機組必須開機約束

機組必須開機約束為

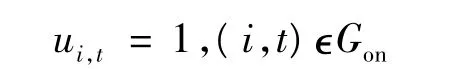
式中，Gon為時段t內必須運行的發電機組集合。

3)機組日利用小時數約束

機組日利用小時數約束為

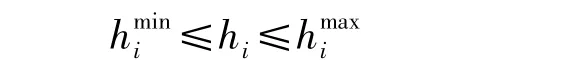
式中，hi為發電機組i的日利用小時數;為發電機組i的日最小利用小時數;為發電機組i的日最大利用小時數。

4)機組啟停時間間隔約束

機組不能頻繁啟停，運行和停運都必須持續一段時間。

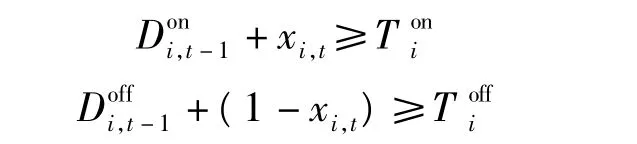
2 求解方法

月度交易計劃編制優化模型是一個復雜的混合規劃問題，傳統的數學優化算法隨著計算規模的擴大，存在“維數災”問題。

粒子群優化算法簡單，可處理各種復雜優化問題，已在多個領域廣泛應用，但不同程度地存在早熟收斂問題。Tabu搜索通過禁忌準則避免迂回搜索，通過藐視準則來赦免一些被禁忌的優良狀態，以保證多樣化的有效探索，最終實現全局最優。借鑒這一思想來改進PSO算法，避免算法陷入局部最優導致的早熟收斂［12］。以改進后的Tabu-PSO算法來求解月度交易計劃編制優化模型。流程如下。

1)參數設置。粒子群個體的維數取優化變量的個數即火電機組數，種群規模M取40。Tabu-PSO算法參數設置:慣性因子w取0.5，學習因子c1=c2=2.0，速度限制取±4.0，禁忌長度L即禁忌對象的任期取5，最大迭代次數Imax取50。

2)初始解生成。隨機生成M個可行解xi，計算各個可行解的目標函數，取M個可行解中的目標函數值最小的可行解作為群體當前的最優解Pg，并將其設置為禁忌對象，任期為L;將M個可行解設置為粒子自身當前的最優解Pi。當前迭代次數置為1。

3)判斷當前迭代次數是否達到最大迭代次數，若不滿足，當前迭代次數累加1:若達到最大迭代次數則輸出群體當前最優解Pg為最終的優化結果。

4)計算各個粒子的飛行速度

各個粒子飛行速度為

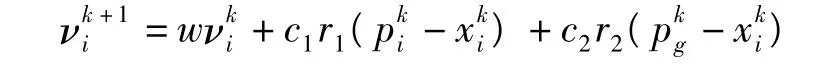
式中，w為慣性因子;c1、c2為學習因子;r1、r2為［0，1］間的隨機數;為粒子未來飛行速度和當前飛行速度;為粒子自身當前的最優解和群體當前的最優解。

5)根據粒子速度產生新的粒子位置(解)

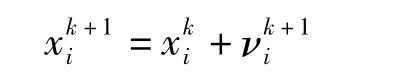
6)查看粒子位置是否被禁，若是則重復步驟4)、5)，若不是，繼續以下步驟。

7)計算粒子新位置(解)的目標函數值，與粒子當前最優解pi對應的目標函數值fi，best比較，若小則將粒子的新位置作為粒子的當前最優解pi，并更新fi，best;選取種群中所有粒子自身當前最優解的最小者，與種群當前最優解比較，若小則更新種群當前最優解pg及相應的目標函數值fg，best，并更新禁忌對象，若未更新種群當前最優解，則遞減禁忌對象的任期，轉入步驟3)。

3 計劃管理

編制好的交易計劃其效果依賴于各個電廠對計劃的執行情況。計劃管理不僅是各個電廠月度開停、出力、發電量等信息的管理，還包含了對各個電廠計劃執行情況的跟蹤與評估。評估計劃執行情況的指標具體定義如下。

1)電量偏差率

用于衡量各個發電機組實發電量對計劃電量的偏差，其定義如下。

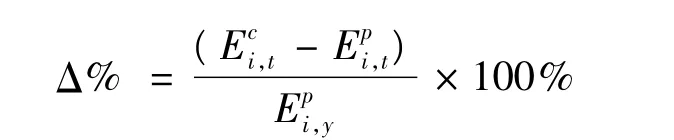
2)偏差均衡率

用于衡量各個發電機組電量偏差相對于平均偏差水平的差異程度，其式為

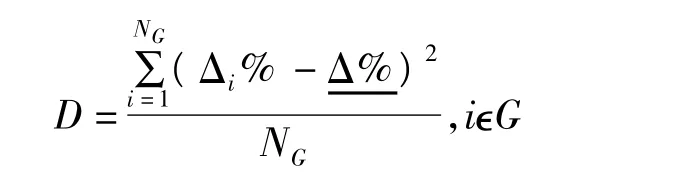
式中，G為發電機組集合，可分別取超發機組和欠發機組進行統計;NG為發電機組集合里發電機組的總臺數;Δi%為發電機組集合里第i臺發電機組的偏差率;Δ%為發電機組集合里發電機組的平均偏差率。

3)合同進度

對各個發電機組分別統計豐水期、枯水期以及全年的合同完成進度，其式為

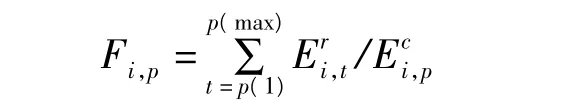
式中，依據變量p的取值，Fi，p分別為發電機組 i的豐水期合同電量完成進度、枯水期合同電量完成進度和年度合同電量完成進度;p(1)分別為豐水期起始時段、枯水期起始時段和年度起始時段;p(max)分別為豐水期結束時段、枯水期結束時段和年度結束時段;為發電機組i已經完成的發電量;分別為發電機組i的豐水期合同電量、枯水期合同電量和年度合同電量。

4 實例

以某省公司2012年數據來驗證模型及方法的實用性。

4.1 計劃編制

月度交易計劃編制模型中系統平衡約束如表1所示(只列出10—12月份的系統電力電量需求)，其中電力需求取該月份典型日的預測負荷，電量需求僅是火電部分的電量需求。

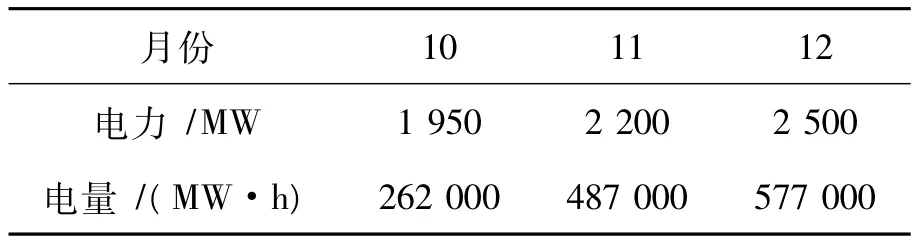
表1 電力電量

月度交易計劃編制模型中機組約束如表2所示(只列出部分信息)，包括了機組的容量、全年的合同電量、豐枯期的合同電量、檢修安排、機組日利用小時數的最大最小值。機組啟停時間間隔，所有機組取值相同，持續開機時間不少于10天，持續停機時間不少于10天。

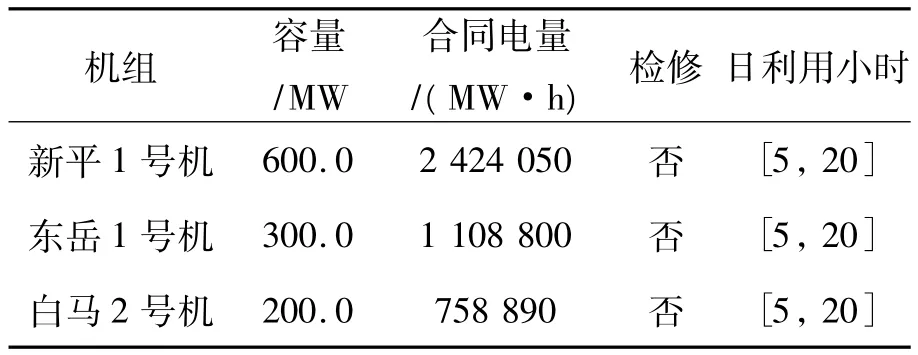
表2 機組運行信息

采用Tabu-PSO分別求解節能調度模式、“三公”調度模式下火電機組月度交易計劃。表3、表4分別是節能調度模式和“三公”調度模式下部分發電機組月度發電計劃(表中的單位均為MW·h)。

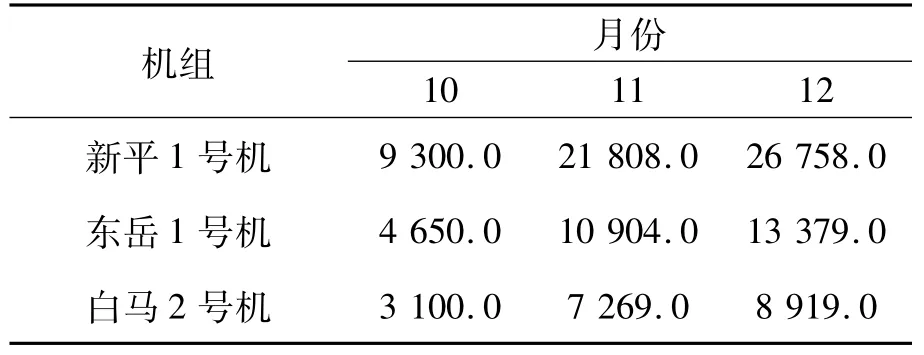
表3 節能調度模式

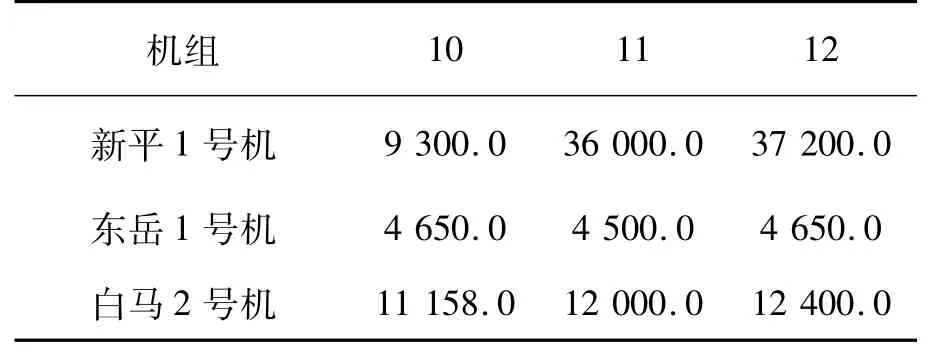
表4 “三公”調度模式

4.2 計劃管理

根據上述算法設計計算軟件，圖1展示了十月份各個發電機組計劃完成情況的評估結果。

畫面上半部分是機組合同完成進度統計分析結果展示:左邊以進程條的形式展示了查詢機組全年合同執行的進度、豐枯期合同執行的進度以及查詢月份合同計劃電量的完成情況;右半部分是所有機組合同完成進度的統計分析結果展示，列表部分展示了全年、豐枯期、查詢月份完成進度靠前、靠后的機組及其合同完成進度，進程條則展示了所有機組平均執行進度。

畫面下半部分展示了上網電量的偏差統計:上面的列表展示了查詢機組全年、豐枯期、查詢月份實發電量與計劃電量之間的偏差;下面的列表則展示了全年、豐枯期、查詢月份實發電量與計劃電量之間的偏差量靠前、靠后的機組及其計劃電量、實發電量、偏差率。

5 結語

針對電力體制新形勢下多種調度模式的發電計劃科學化管理要求，提出了考慮多種調度模式的月度交易計劃統一編制模型，通過設置不同的目標函數來反映不同的調度模式;模型采用禁忌-粒子群算法進行求解，利用禁忌算法的局部搜索能力來改善粒子群算法的“早熟”收斂。需指出所提模型里的約束只包含了機組的運行約束，如何有效地考慮系統的安全約束，將是后續進一步研究的內容。

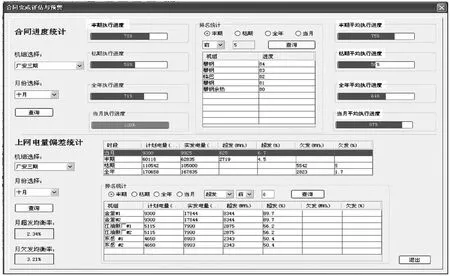
圖1 計劃管理

［1］湯偉，王漪，于繼來，等.編制直調火力發電單元月度電能交易計劃的綜合耗量優化法［J］.中國電機工程學報，2009，29(5):64-70.

［2］Wang S J，Shahidehpour S M，Kirschen D S，et al.Short-term Generation Scheduling With Transmission and Environmental Constraints Using an Augmented Lagrangian Relaxation［J］.IEEE Transactions on Power Systems，1995，10(3):1294-1301.

［3］Huse E S，Wangensteen I，Faanes H H.Thermal Power Generation Scheduling by Simulated Competition［J］.IEEE Transactions on Power Systems，1999，14(2):472-477.

［4］Abido M A.Environmental/Economic Power Dispatch U-sing Multi-objective Evolutionary Algorithms［J］.IEEE Transactions on Power Systems，2003，18(4):1529-1537.

［5］張國立，李庚銀，謝宏，等.日前和實時市場統一電能交易模型［J］.中國電機工程學報，2006，26(21):50-56.

［6］初壯，于繼來.初期電力市場確定電網日發電計劃的模型與方法［J］.電力系統自動化，2006，30(22):43-47.

［7］Yu Z，Sparrow F T，Nderitu D.Long-term Hydrothermal Scheduling Using Composite Thermal and Composite Hydro Representations［J］.IEE Proceedings-Generation，Transmission and Distribution，1998，145(2):210-216.

［8］Ferrero R W，Rivera J F，Shahidehpour S M.A Dynamic Programming Two-stage Algorithm for Long-term Hydrothermal Scheduling of Multireservoir Systems［J］.IEEE Transactions on Power Systems，1998，13(4):1534-1540.

［9］Fu Y，Shahidehpour M，Li Z.Long-term Security-constrained Unit Commitment Hybrid Dantzig-Wolfe Decomposition and Subgradient Approach［J］.IEEE Transactions on Power Systems，2005，20(4):2093-2106.

［10］王漪，于繼來，柳焯.基于月度競價空間滾動均衡化的年中標電量分解［J］.電力系統自動化，2006，30(17):24-27.

［11］楊爭林，唐國慶.全周期變時段“三公”調度發電計劃優化模型［J］.電網技術，2011，35(2):132-136.

［12］許立雄，呂林，劉俊勇.基于改進粒子群優化算法的配電網絡重構［J］.電力系統自動化，2006，30(7):27-30，30.