空間機器人多臂精準協(xié)同控制技術(shù)

賀 亮，王有峰，吳 蕊，謝 冉

(1.上海航天控制技術(shù)研究所，200233上海;2.上海市空間智能控制技術(shù)重點實驗室，200233上海;3.北京航空航天大學宇航學院，100191北京)

近年來，以在軌服務(wù)技術(shù)為代表的空間應用領(lǐng)域得到了突飛猛進的發(fā)展，為了奪取技術(shù)制高點，各航天強國都投入巨資開展關(guān)鍵技術(shù)攻關(guān).目前，以美歐為代表的航天強國已經(jīng)完成了諸如模塊更換、在軌組裝以及燃料加注［1-2］等項目的空間演示驗證，并且繼續(xù)制定一系列新的計劃拓寬在軌服務(wù)的內(nèi)容和手段.

空間機器人作為在軌服務(wù)的一種有效手段［3］，尤其受到美德等國的青睞.實踐證明，空間機器人由于具有自主、靈活和安全等特點，在抓捕和操作目標的過程中表現(xiàn)出了其它工具所不具備的獨特優(yōu)勢，因此更加適合對精度要求較高的在軌服務(wù)項目.

空間機器人按機械臂的數(shù)量可以劃分為單臂空間機器人和多臂空間機器人.隨著任務(wù)復雜程度的不斷增加，單臂空間機器人將不能滿足對操作精度要求較高的在軌服務(wù)任務(wù)，相反，多臂空間機器人則能較好地滿足此類任務(wù)的需求，通過多條機械臂協(xié)同工作，快速靈活地完成抓捕、更換以及拖曳等操作.目前，國外已經(jīng)制定了多項多臂空間機器人的研究計劃，典型的有美國的SUMO/FREND 計劃［4］、NM-5計劃以及鳳凰計劃.這些計劃都涉及到一項核心技術(shù)——機械臂協(xié)同控制技術(shù)，本文正是以此為背景，進行空間機器人多臂精準協(xié)同控制技術(shù)研究.

多臂空間機器人由于工作在零過載、微重力的空間環(huán)境中［5-6］，故安裝在其上的機械臂通常設(shè)計為輕柔的細長桿型結(jié)構(gòu)，這使得它成為一種典型的多柔體系統(tǒng);同時，由于機械臂運動產(chǎn)生的反作用力和力矩會改變本體的位置和姿態(tài)，即機械臂和本體之間存在著運動學和動力學耦合，導致地面固定基座操控平臺的控制技術(shù)不能直接應用到多臂空間機器人上［7-8］，因此需要利用多柔體系統(tǒng)動力學［9］的理論和方法建立柔性多臂空間機器人動力學模型.

在空間機器人建模方面，國內(nèi)外學者已經(jīng)取得了許多研究成果，典型的有美國的VAFA Z和DUBOWSKY S提出的虛擬機械臂(VM)概念［10］中國的梁斌提出的動力學等價機械臂［11］以及李瑰賢等［12］采用牛頓-歐拉法建立的動力學方程.為了得到更具普遍性的結(jié)果，本文采用Kane方法建立系統(tǒng)動力學模型.

1 系統(tǒng)建模

1.1 系統(tǒng)構(gòu)型

本文研究的空間機器人包含3條機械臂，每條機械臂由7節(jié)構(gòu)成，其構(gòu)型如圖1所示.

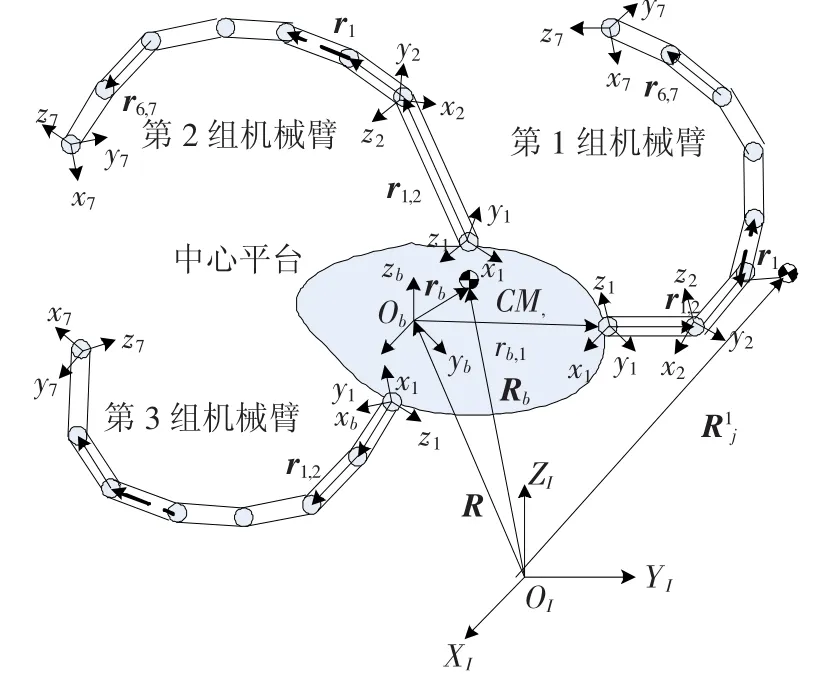
圖1 多臂空間機器人構(gòu)型

1.2 基本參數(shù)定義

1.2.1 坐標系單位基向量

1)中心體連體坐標系Sb(Obxbybzb)

原點Ob位于中心體質(zhì)心，xb、yb和zb與中心體慣性主軸平行且滿足右手定則.

設(shè)系統(tǒng)有i條機械臂，第i條臂有ni節(jié)，定義第i條臂中第j節(jié)臂的機械臂坐標系原點位于第j節(jié)臂與其內(nèi)接體的鉸鏈oi j處，坐標系各軸與第j節(jié)臂固連.

1.2.2 位置參數(shù)定義

接下來給出圖1中各矢量的定義:

1.2.3 運動參數(shù)

1.2.3.1 角速度

1.2.3.2 線速度

1)中心體線速度

2)第i條機械臂線速度不妨以j＞2為例，對R?i j求導，j=1 時同理可得

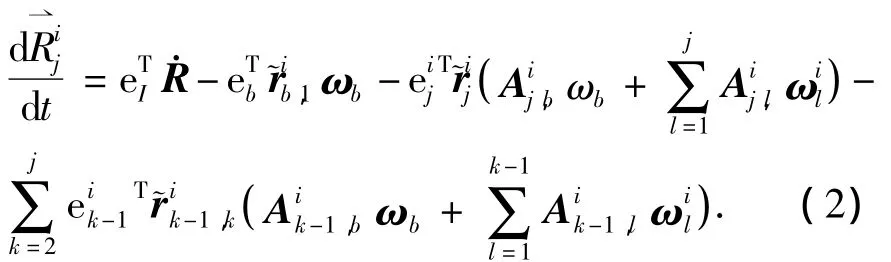
1.2.3.3 加速度

1)中心體質(zhì)心加速度

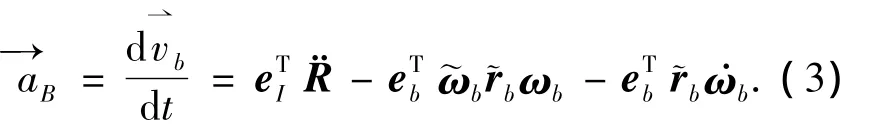
2)第i條機械臂(以j＞2為例j=1時同理)

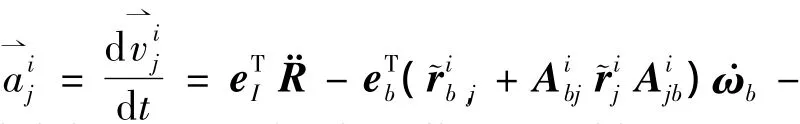
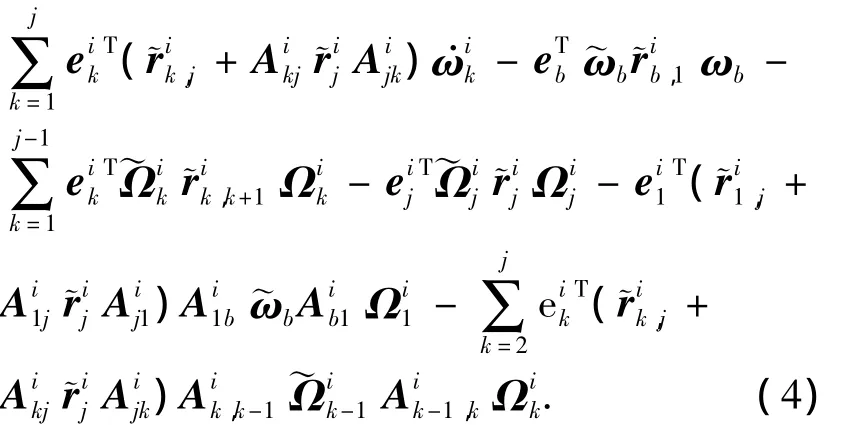
1.3 多臂空間機器人Kane方程

1.3.1 引理

理想約束條件下，系統(tǒng)若處于平衡，則

這個方程就是Kane方程，式中f*Ⅰk，f*ek和f*Nk分別稱為系統(tǒng)與偏速度Wk對應的第k階廣義慣性力、廣義主動力和廣義彈性力.

1.3.2 機械臂系統(tǒng)參數(shù)計算

1.3.2.1 廣義慣性力

1)中心體慣性力

中心體第1階廣義慣性力為

中心體第2階廣義慣性力為

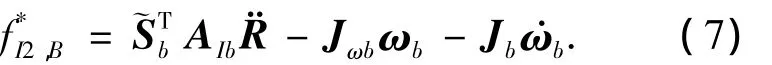
中心體第k(k＞2)階廣義慣性力為

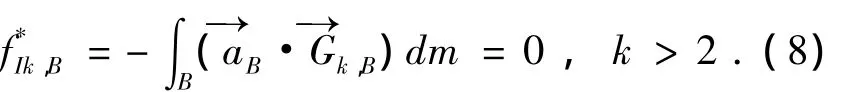
1.3.2.2 第i條機械臂第j節(jié)臂的慣性力

1)第1階廣義慣性力

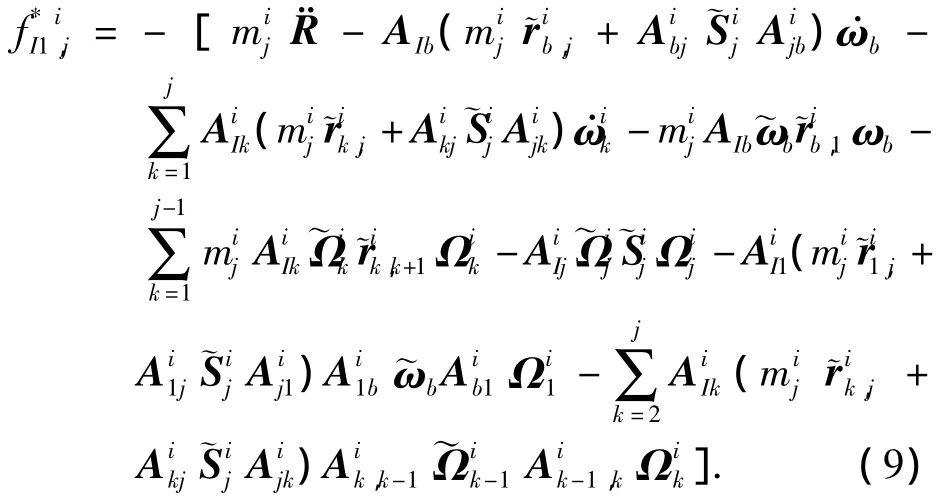
2)第2階廣義慣性力

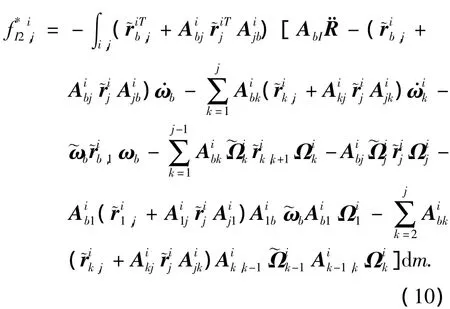
3)第2+7*(i-1)+l階廣義慣性力

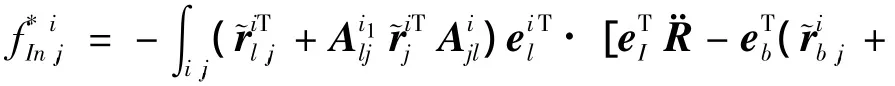
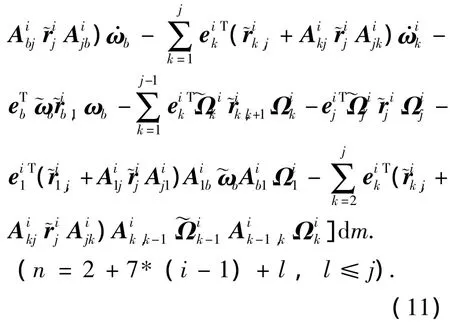
1.3.2.3 廣義主動力

系統(tǒng)所受外力主要包括以下3個部分:

1)作用于中心體上的力F;

2)作用于中心體上的力矩T;

3)作用于機械臂各關(guān)節(jié)處的控制力矩，對應于第i條機械臂第j節(jié)臂的關(guān)節(jié)處的控制力矩記為Tij.

1.3.3 空間機器人各體動力學方程

1.3.3.1 中心體平動方程

中心體平動方程對應于第1階廣義速度R，將式(6)和式(9)式代入式(5)，因此有

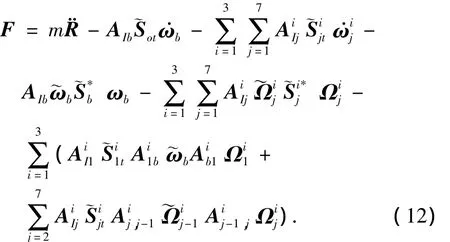
1.3.3.2 中心體轉(zhuǎn)動方程

中心體轉(zhuǎn)動方程對應于第2階廣義速度ωb，將式(7)和式(10)式代入式(5)，因此有

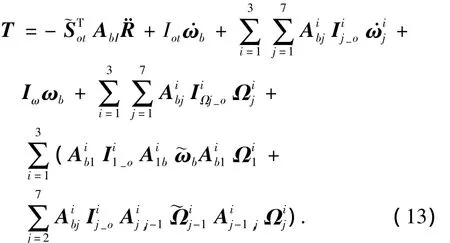
1.3.3.3第i條機械臂第j節(jié)臂的轉(zhuǎn)動方程

第1節(jié)臂轉(zhuǎn)動方程對應于第2+7*(i-1)+1階廣義速度ωi1，將(8)和(11)式代入(5)，因此有

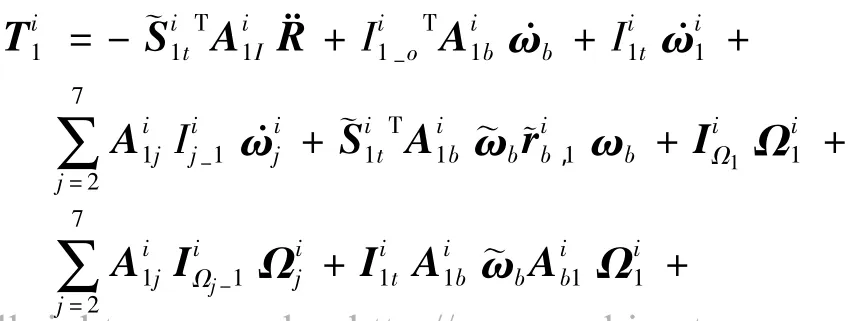
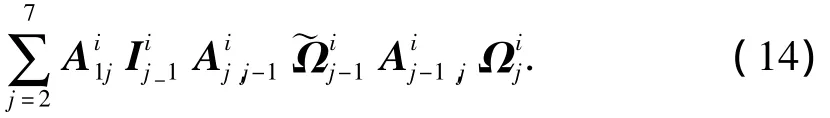
其他各節(jié)臂轉(zhuǎn)動方程類似，不再重復.

1.3.4 空間機器人系統(tǒng)矩陣形式完整動力學方程將中心體平動方程和轉(zhuǎn)動方程整合得到機械臂系統(tǒng)的動力學方程為

2 開鏈系統(tǒng)控制器設(shè)計

空間機器人軌跡跟蹤控制方面，國內(nèi)外學者已經(jīng)取得了大量研究成果，典型的有YOSHIDA K等［13］人提出的雙臂補償控制方法和林成金［14］提出的軌跡跟蹤魯棒控制方法.這些方法需要進行繁瑣的矩陣運算，難以實現(xiàn)機械臂軌跡實時跟蹤控制，為此，本文基于李雅普諾夫穩(wěn)定性理論，推導得出了較為簡潔的控制算法，詳細過程如下文.

2.1 動力學方程簡化

在控制器設(shè)計過程中，忽略質(zhì)心平動運動的影響，同時考慮到機械臂的運動過程一般比較緩慢，中心體的角速度一般也是小量，因此方程中的非線性耦合項可以作為高階小量忽略不計，于是系統(tǒng)動力學方程可以重新寫成下述的線性形式:

式中:

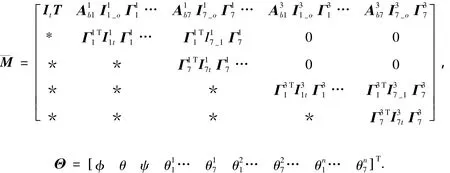
小角度假設(shè)下有

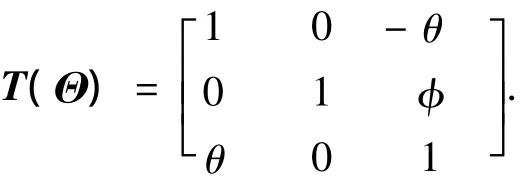
式(16)雖然形式上很簡潔，但實際上系統(tǒng)質(zhì)量矩陣與機械臂各關(guān)節(jié)轉(zhuǎn)角相關(guān)，且計算表達式非常復雜，但考慮到整個系統(tǒng)運動較為緩慢，且機械臂的質(zhì)量和慣量較小，因此可采用“凍結(jié)系數(shù)法”來計算質(zhì)量陣.記更新時間段之內(nèi)M的常值取為，則該時間段內(nèi)控制器設(shè)計模型為

不同時段內(nèi)除Mc的取值不同外，系統(tǒng)模型形式無變化，選取式(17)作為控制方程.

2.2 控制律設(shè)計

定義狀態(tài)量為實際值與期望值之間的誤差為

取中間變量

式中:K為對稱的正定矩陣.取Lyapunov函數(shù)

則有

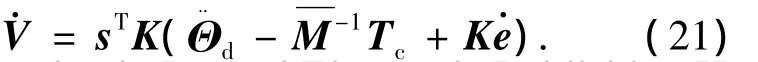
取控制力矩

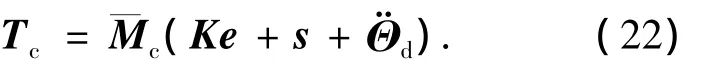
得到

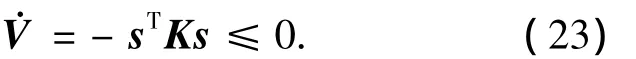
從而說明函數(shù)V是定負的，因此由式(23)可知，函數(shù)V的解對t的全導數(shù)是定負的，也即說明該控制律能夠保證誤差收斂且是漸近收斂的.

3 數(shù)值仿真

首先給出多臂多自由度機械臂系統(tǒng)的仿真參數(shù)，表1給出3條機械臂在中心體上的安裝位置.

表1 3條機械臂在中心體上的安裝位置

表2給出第1條臂第2～7節(jié)的安裝位置，由于3條機械臂完全相同，故在此只給出其中1條的數(shù)據(jù).

表3給出中心體、各條機械臂以及目標的質(zhì)量特性參數(shù)，3條機械臂完全相同，只給出第1條臂的參數(shù).

給定中心體姿態(tài)角初始狀態(tài)為［2 3 2］Tdeg，第一條臂各關(guān)節(jié)相對于標稱狀態(tài)的初始轉(zhuǎn)角為［-7.02 155.24-142.08-13.15-3.37 0 0］Tdeg，中心體和機械臂各關(guān)節(jié)角速度均為零，考慮到實際控制力矩的大小有限，限定中心體的最大控制力矩為umax-b=［100100100］TN·m，各關(guān)節(jié)最大控制力矩為50 N·m，利用Matlab仿真得到結(jié)果如圖2～5所示.

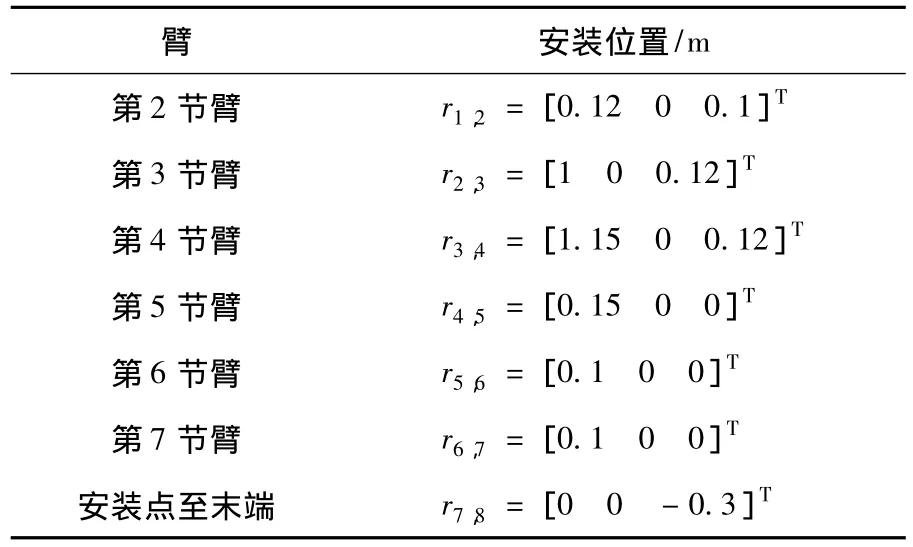
表2 第1條臂第2～7節(jié)的安裝位置

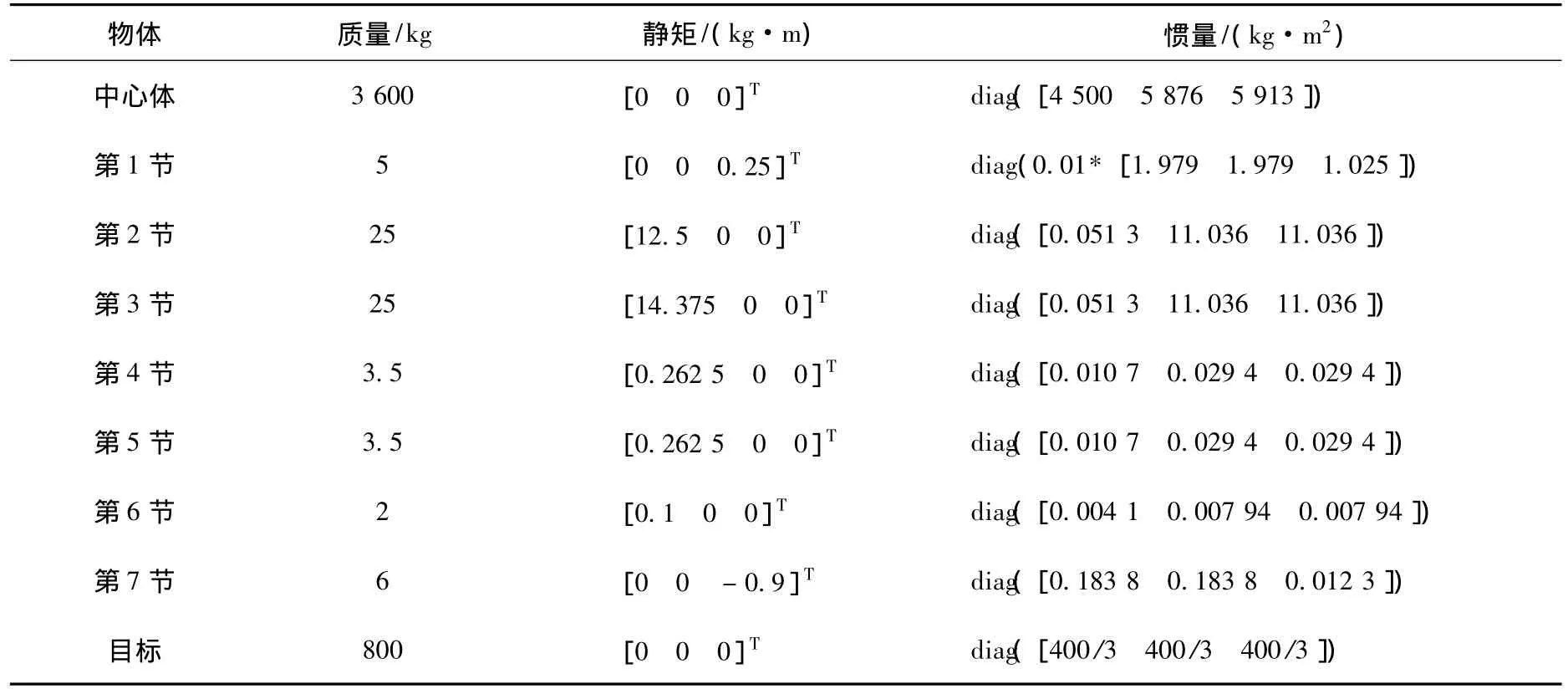
表3 中心體、第1條機械臂各節(jié)以及目標的質(zhì)量特性參數(shù)

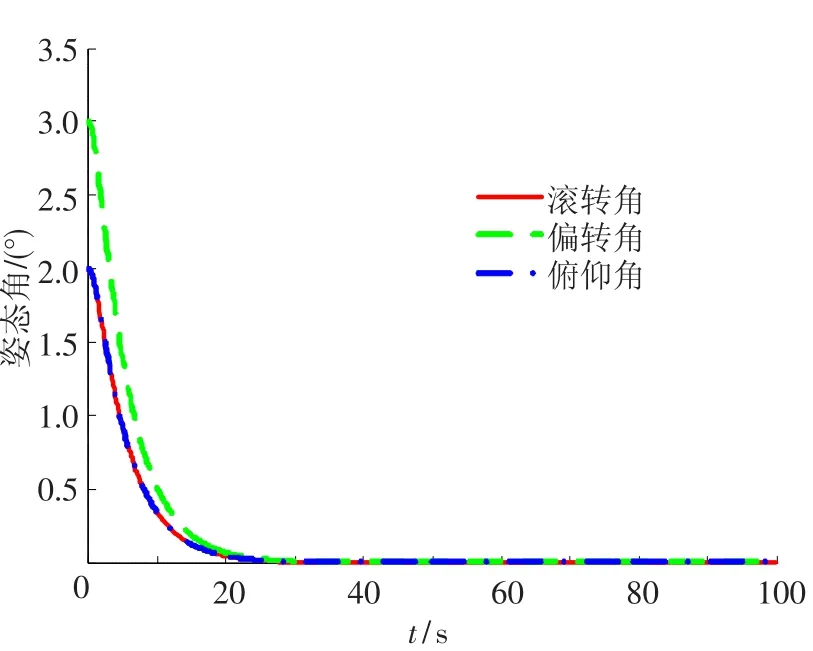
圖2 中心體在控制力矩作用下姿態(tài)角變化曲線

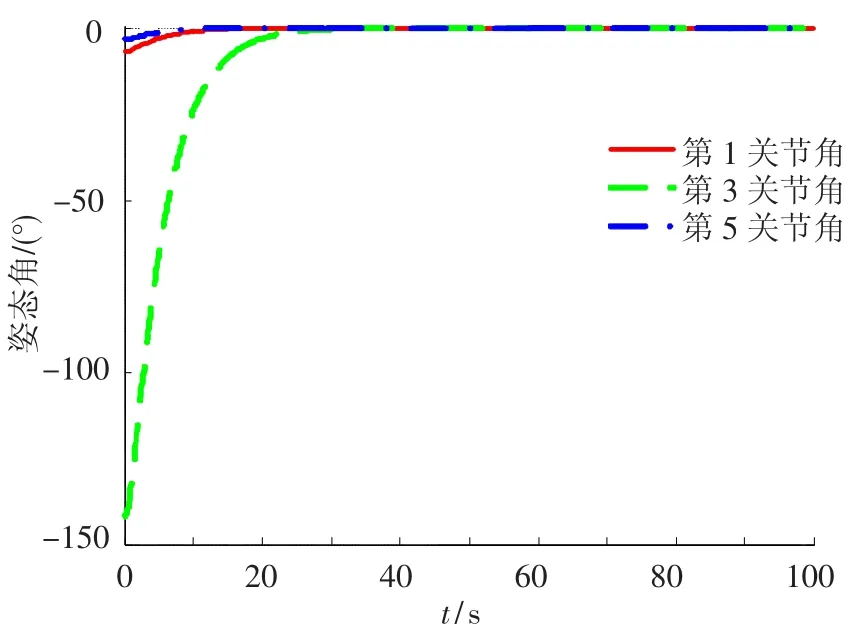
圖3 第1條臂第1、3、5關(guān)節(jié)角在控制力矩作用下的變化曲線

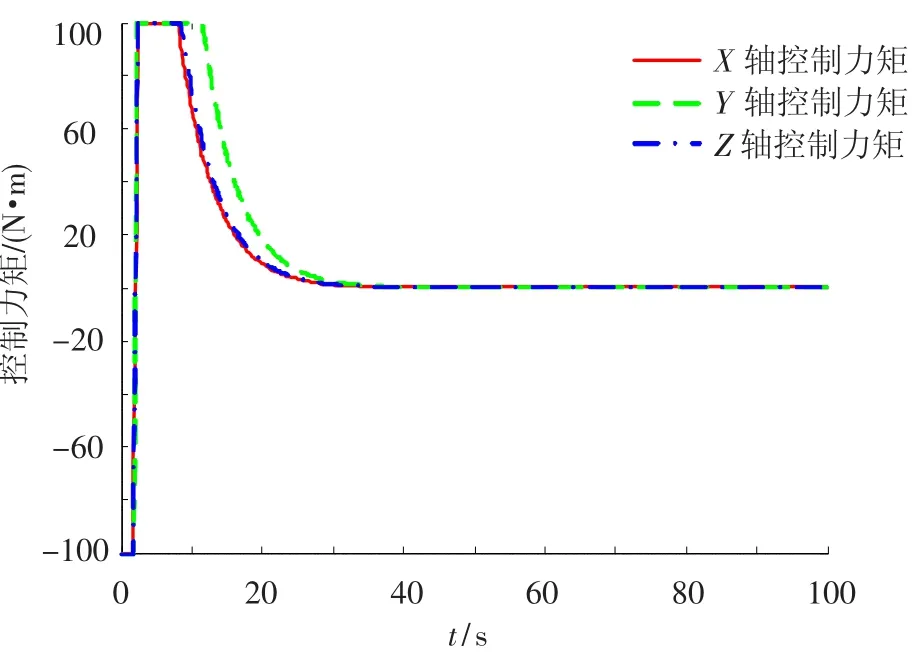
圖4 中心體所受的控制力矩變化曲線

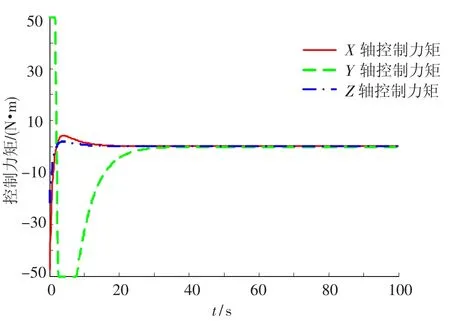
圖5 第1條臂第1、3、5關(guān)節(jié)所受的控制力矩變化曲線

第2、4、6關(guān)節(jié)的仿真結(jié)果類似，文中不再給出.從圖2至圖5可以看出，在控制力矩受約束的情況下，最終平臺姿態(tài)和關(guān)節(jié)轉(zhuǎn)角都能很好的跟蹤期望值(姿態(tài)角和關(guān)節(jié)轉(zhuǎn)角的期望值都取為零)，并且姿態(tài)角控制精度達到了1×10-9rad，與梁斌［10］提出的動力學等價機械臂(DEM)方法相比，具有更高的控制精度，與林成金［13］提出的軌跡跟蹤魯棒控制方法相比，具有更高的穩(wěn)定.

4 結(jié)論

1)利用Kane方法建立了具有3條7自由度的空間多臂機器人動力學方程，并且只要改變模型中的求和上限，即可改變機械臂的數(shù)量和自由度所得的結(jié)果可以推廣到具有n條m個自由度的空間機器人，n，m∈Z.

2)針對開鏈情況下中心體和機械臂的協(xié)同控制問題，設(shè)計了基于李雅普諾夫函數(shù)的機械臂運動跟蹤控制律，實現(xiàn)了機械臂在三維空間抓捕目標過程中對期望軌跡的跟蹤.

3)通過數(shù)值仿真可知，本文所設(shè)計的控制律其他方法相比具有更高的控制精度和穩(wěn)定性，并且在力矩大小受限與不受限兩種情況下均能實現(xiàn)機械臂末端軌跡跟蹤.

4)本文所建立的模型具有一定的開放性，只要在現(xiàn)有模型中加入彈性坐標系即可將模型轉(zhuǎn)化為柔性機械臂系統(tǒng)，而不需要重新推導方程.

［1］李廣興，肖余之，卜劭華等.空間站組裝過程姿態(tài)控制方案研究［J］.載人航天，2012，18(01):22-29.

［2］敬忠良，袁建平.航天器自主操作的測量與控制［M］.中國宇航出版社，2011.

［3］LANIUS R，MCCURDY H.Robots in Space［M］.Baltimore:The Johns Hopkins University Press，2008:1-2.

［4］BOSSE A B，BARNDS J W，BROWM M A.SUMO:spacecraft for the universal modification of orbits［J］.Proc.of SPIE，2004，5419:36-46.

［5］MURARD S.Extended online nonholonomy criterion of a drifted free-flying space robot with-without Interaction with a target satellite［C］//IEEE/ISIE2006，Montreal，2006:80-85.

［6］朱戰(zhàn)霞，袁建平.航天器操作的微重力環(huán)境構(gòu)建［M］.中國宇航出版社，2013:13-16.

［7］KAZUYA Y.Engineering test satellite VII flight experiments for space robot dynamics and control:theories on laboratory test beds ten years ago，now in orbit［J］.The International Journal of Robotics Research，2003，22(5):321-335.

［8］KATSUHIKO Y.Attitude control of space robot by arm motion［J］.Journal of Guidance，Control and Dynamics，1994，17(5):1050-1054.

［9］楊樂平，朱彥偉，黃渙.航天器相對運動軌跡規(guī)劃與控制［M］.國防工業(yè)出版社，2010.

［10］VAFA Z，DUBOWSKY S.The kinematics and dynamics of space manipulators:the virtual manipulator approach［J］.Journal of Robotics Research，1990，9(4):3-21.

［11］梁斌，劉良棟，李庚田等.空間機器人的動力學等價機械臂［J］.自動化學報，1998，24(6):761-767.

［12］李瑰賢，袁景陽，柳長安.多臂自由飛行空間機器人協(xié)調(diào)操作動力學分析［J］.哈爾濱工業(yè)大學學報，2007，39(3):374-377.

［13］YOSHIDA K，KURAZUME R，UMETANI Y.Torque optimization control in space robots with a redundant arm［J］.IEEE/RSJ In Workshop on Intelligent Robots and Systems，1991:1647-165.

［14］林成金，陳力.自由漂浮雙臂空間機器人基于速度濾波器的慣性空間軌跡跟蹤魯棒控制［J］.空間科學學報，2012，32(5):757-764.