采空區充填效果的隨機規律研究

郭 力 何朋立

(洛陽理工學院土木工程系)

隨著我國經濟的迅速發展，對能源的需求不斷增加，促使煤炭開采規模日益增大，易采資源日趨減少，對“三下一上”(建筑物下、鐵路下、水體下和承壓含水層上)壓煤合理開采的意愿越來越強烈;同時，煤炭開采中還伴隨著大量廢棄物的排放以及塌陷區的出現，按傳統的處理方式必然會對環境產生危害。而利用充填采煤技術，可較好地解決這兩方面的問題。一方面因其對巖層擾動小，具有控制巖層移動與地表沉陷的作用，另一方面可以有效利用煤礦廢棄物實施充填，減少廢棄物的排放。因此，充填開采是煤礦綠色開采技術體系的主要內容之一，是解決煤礦開采環境問題和“三下一上”壓煤開采問題的有效途徑。

實際工程中，由于充填工藝、施工條件以及充填材料自身的特點等多個影響因素，不論何種充填方式，對采空區的充填都無法達到理想狀態，其充填效果或程度不可能是絕對連續和均勻的。采空區充填效果的主要影響因素是充填材料和充填程度。此處充填程度是對充填方案中所要充填的采空區而言，也就是說，所要充填的采空區的理想或設計充填程度是100%，而實際操作中要達到這個程度幾乎是不可能的。即使充填程度都是理想的100%，其充填材料也非完全連續和均勻的。顯然，在實際中這是一個隨機問題，其相關充填參數是隨機變化的。由此，本研究借助隨機有限元方法對此問題進行分析，以探究采空區充填效果隨機變化情況下，圍巖穩定性及地表沉降的統計規律。

1 計算模型

煤層埋深400 m，煤層厚度為3 m，不考慮煤層傾斜，即煤層水平分布。煤層直接頂為泥質粉砂巖，厚度為20 m。泥質粉砂巖之上至地面為表土層，表土層厚度為380 m。煤層直接底為中砂巖。計算時，模型上邊界取至地面，模型下邊界取煤層之下30 m，模型寬度取為600 m。則計算模型取礦區截面，總尺寸為(寬×高)600 m×433 m，采空區豎直尺寸為3 m，水平尺寸為600 m。采用平面應變模型，模型從上至下為表土層(厚380 m)、粉砂巖層(厚20 m)、煤層(厚3 m)、中砂巖層(厚30 m)。不考慮地表的附加荷載。

2 隨機計算

2.1 方法選擇

隨機計算采用蒙特卡羅(Monte－Carlo)有限元法，該法通過在計算機上產生的樣本函數來模擬系統的隨機輸入量的概率特征，并對于每個給定的樣本點，對系統進行確定性的有限元分析，從而得到系統的隨機響應的概率特征。蒙特卡羅有限元法是目前最常用的統計逼近法，可以獲得輸出隨機變量與輸入隨機變量之間的關系。

2.2 隨機輸入變量

采空區充填效果的主要影響因素是充填材料和充填程度。不同的充填材料有著不同的力學特性，荷載作用下其表現有差異，因而對圍巖穩定性及地表沉降有著不同的影響。充填程度直接影響到圍巖和充填體的變形和受力。實際充填工程中，充填程度難以達到100%，但也不會存在太大的差距。因而當充填程度達不到100%時，采空區上部圍巖存在一定的臨空面。但這個臨空面不會一直存在，隨著變形的發展，上部圍巖將會與充填體接觸，充填體就會開始工作。

以上兩個影響因素分別屬于充填體的材料特性和幾何尺寸，影響到充填體受載后的性能。由力學觀點來看，二者均是改變了充填體剛度。本研究將充填體作為彈性體進行計算，由相關計算結果對比來看，影響彈性體剛度的主要是彈性模量。同時由于隨機模擬計算需要大量的抽樣，計算量比較大，而對彈性模量進行抽樣計算不會對計算模型的幾何建構產生影響，這在一定程度上降低了隨機模擬計算的計算量，因而本研究將充填體的彈性模量作為隨機輸入變量。

對于隨機輸入變量，必須制定每個變量的分布函數類型。其中高斯分布是一個非?；竞统Ｓ玫慕y計分布函數，一般用于描述許多物理現象的測量數據。而一般實際物理現象雖然服從高斯分布，但極限值是被限制的，或者要通過質量控制手段將樣本所測數值規定在一個范圍內。充填體的彈性模量也符合這一規律，選用截斷高斯分布作為隨機輸入變量的分布函數。

由此，理想條件下充填體的彈性模量取為350 MPa，考慮到實際情況，將0.9×350=315 MPa作為隨機輸入變量的均值，變異系數取0.2(變異性中等)，則標準差為315×0.2=63 MPa，最小值為0.8×350=280 MPa，最大值350 MPa。

2.3 隨機輸出變量

對于采空區充填參數隨機變化所帶來的影響，從圍巖穩定性及地表沉降兩方面進行考量。當隨機計算的循環次數達到一定數量，特征模型具有對稱性。因此在計算模型中地表處取1點就可以代表地表沉降的變化規律。取模型中地表水平邊界中點(對稱軸處)的豎向位移作為一個隨機輸出變量，樣本單位為cm，取名為UY。從采空區頂板和充填體兩方面的受力情況來說明圍巖穩定性，同理，本研究將模型寬度一半處(對稱軸處)采空區頂板內1點的豎向位移、第一主應力以及等效應力

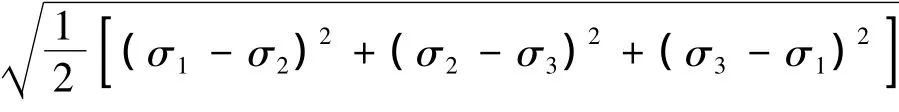
作為隨機輸出變量，樣本單位分別為cm、MPa和MPa，分別取名為DB_UY、DB_S1和 DB_SEQV。同時，將模型寬度一半處充填體內1點的第一主應力和等效應力也作為隨機輸出變量，樣本單位分別為MPa和MPa，分別取名為CTT_S1和CTT_SEQV。

由此，經過大量隨機抽樣計算后就可以得到以上這些隨機輸出變量的統計規律，從而可以分析采空區充填效果隨機變化情況下，對圍巖穩定性及地表沉降的影響規律。

3 采空區全充填

首先探討煤層全開采、采空區進行全充填的情況。此時，若將充填體的彈性模量在整個模型寬度內保持一樣的波動，這是不合理的。應將充填體劃分為若干個區間，每個區間的充填效果是獨立的，即將每個區間內的充填體彈性模量均作為隨機輸入變量，保持各自獨立。若充填體劃分的區間過多，隨著隨機輸入變量抽樣次數的增加，會使得整個模型的充填體彈性模量有均勻化的趨勢，不存在明顯的統計規律。因此，此處將充填體劃分為10個區間，每個區間寬度是60 m。

計算進行500次循環。隨著抽樣次數的增加，均值和標準差是逐漸收斂的，且曲線趨向水平，說明循環次數和精度是足夠的，樣本數據是穩定的。直方圖顯示，樣本數據接近概率函數分布，較為光滑，沒有較大的間隙。圖1給出了輸出變量UY的均值和標準差的樣本歷史以及樣本直方圖，其余5個輸出變量的均值和標準差的樣本歷史以及樣本直方圖在形態上與輸出變量UY的較為接近，此處不再一一列出。

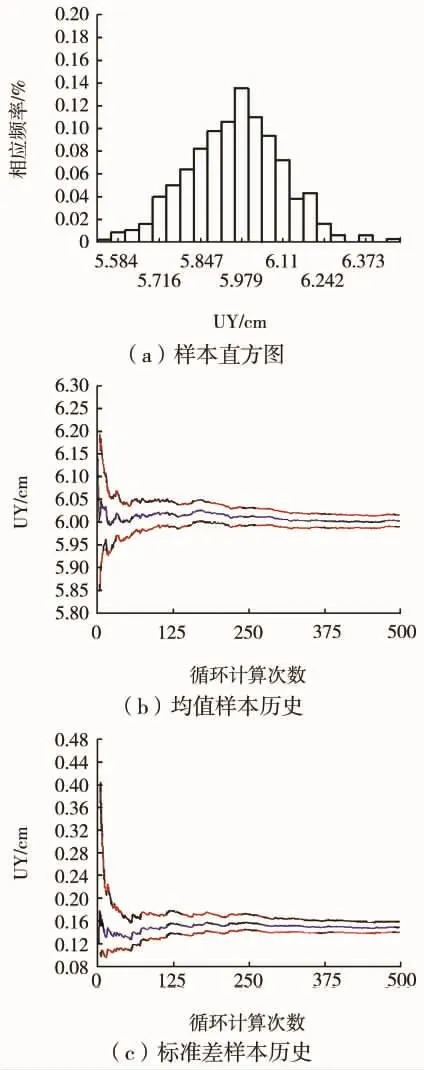
圖1 輸出變量樣本直方圖、均值和標準差樣本歷史

表1給出輸出變量的樣本均值、樣本標準差、變異系數、最大值、最小值以及樣本最大值與均值的比值。整體來講，6個輸出變量的變異系數都很小。相比較而言，地表沉降與采空區頂板沉降這2個豎向位移輸出變量的變異系數比較大，其中采空區頂板沉降變異系數的數值最大。而其余與應力有關的輸出變量的變異系數都比較小。這說明，在全充填的條件下，地表沉降與采空區頂板沉降對充填效果的變化比較敏感，其中與采空區相接的頂板最敏感。而充填效果的波動對應力有關的參數影響并不明顯。這一點從樣本最大值與均值的比值也可以看出。

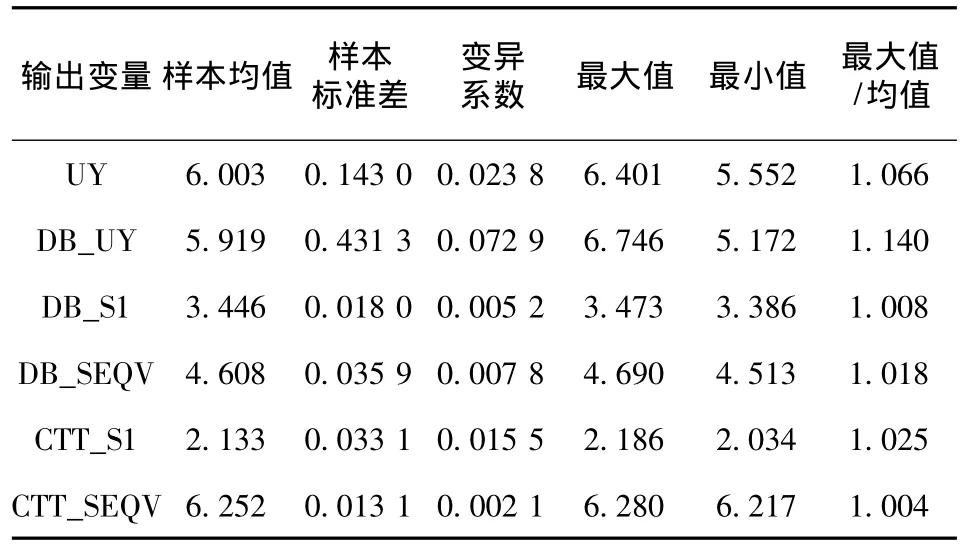
表1 全充填時輸出變量樣本的相關參數

4 采空區部分充填

部分充填也是煤層全開采采空區常采用的充填方式。此時，同樣將采空區劃分為10個區間，每個區間寬度是60 m，其中40 m進行充填，20 m不充填。也就是每充填40 m范圍的采空區，留出20 m范圍不充填，之后繼續進行充填。同樣，每個區間內充填部分的充填效果視為獨立的。

計算進行500次循環，樣本的均值和標準差是逐漸收斂的，且曲線趨向水平，說明循環次數和精度是足夠的，樣本數據是穩定的。直方圖顯示，樣本數據接近概率函數分布，較為光滑，沒有較大的間隙，此處不再一一列出。

部分充填情況下的采空區中一定比例的范圍是不充填的，對于隨機問題來說，就是這部分采空區參數是固定的，不參與隨機計算。與全部充填相比，部分充填的計算模型中隨機變量所包含的范圍和參與波動的范圍減小了。

從表2給出的數據來看，整體上部分充填情況的各輸出變量的變異系數均有較大的變化。同樣，地表沉降與采空區頂板沉降這2個輸出變量的變異系數比較大，其中采空區頂板沉降變異系數的數值最大。與之前全部充填的情況相比，此處地表沉降與采空區頂板沉降的樣本均值都有較明顯的增大，而二者的變異系數是減小的，但采空區頂板沉降的變異系數變化不大。由于存在一定厚度的表土層，采空區充填方式的改變，其充填效果的隨機性對地表沉降的影響比較明顯。

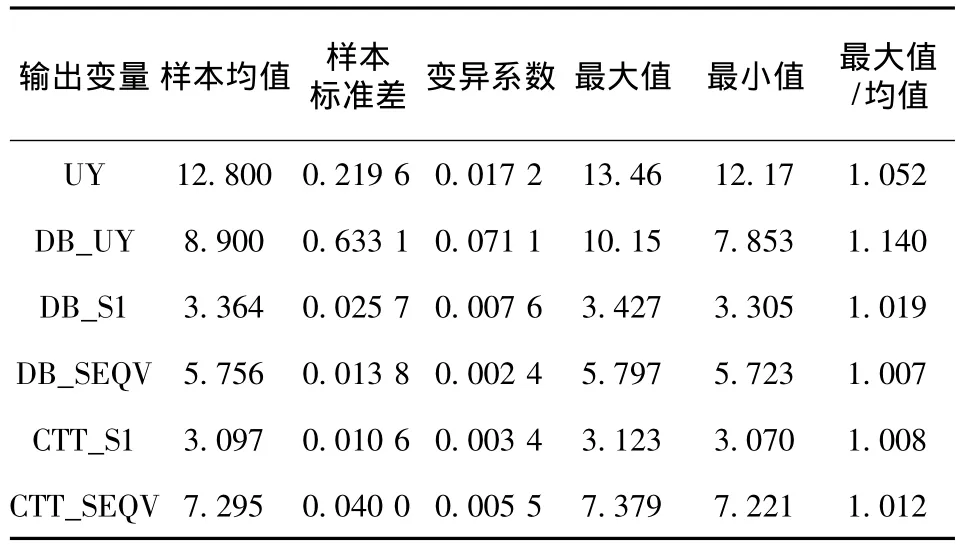
表2 部分充填時輸出變量樣本的相關參數

5 條帶式開采

此處對煤層條帶式開采出現的采空區進行全充填。采出條帶寬度為40 m，保留條帶寬度為20 m。如此，就相當于同樣將采空區劃分為10個區間，每個區間寬度是60 m，其中40 m進行充填，20 m保留為煤層。也就是采空區充填后，每40 m的充填體之間保留20 m為煤層。同樣，每個區間內充填部分的充填效果視為獨立的。

計算進行500次循環，樣本的均值和標準差是逐漸收斂的，且曲線趨向水平，說明循環次數和精度是足夠的，樣本數據是穩定的。直方圖顯示，樣本數據接近概率函數分布，較為光滑，沒有較大的間隙，此處不再一一列出。

將此情況的計算模型中每個區間內保留的20 m寬度的煤層換為充填體材料，就與全充填情況的計算模型是一樣的;將保留的煤層刪除，就與部分充填情況的計算模型是一樣的。從表3給出的數據來看，與之前的全充填與部分充填情況相比，由于保留了一定比例的煤層不開采，6個輸出變量的樣本均值均減小了，有利于圍巖穩定性及地表沉降的控制。

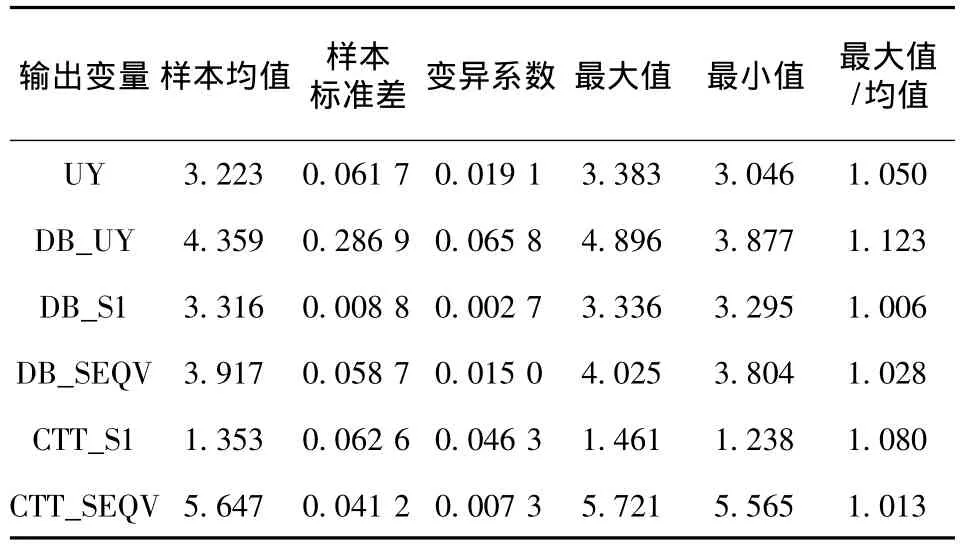
表3 條帶式開采時輸出變量樣本的相關參數

從地表沉降與采空區頂板沉降這2個輸出變量的變異系數來看，條帶式開采這種情況下的數值更接近于全開采部分充填的情況，這是由于相對于全充填情況，二者均存在部分采空區是固定的，不參與隨機計算。

6 結語

(1)對比3種情況計算得到的樣本均值，條帶式開采由于保留了一定比例的煤層不開采，對于地表沉降的控制和圍巖穩定性都是有利的。而對于煤層全開采，采空區全充填無疑是更理想的。

(2)根據本研究的計算模型與思路，且經過次數比較多的隨機抽樣計算，由輸出變量的變異系數來看，6個輸出變量對于采空區充填效果的波動并不敏感。相比較而言，地表沉降與采空區頂板變形對于充填效果的波動要更敏感一些。采空區的充填效果主要影響圍巖的變形，進而影響地表的沉降，而對于圍巖以及充填體自身受力的影響并不明顯。

(3)多次抽樣計算中各輸出變量存在最大值與最小值，說明多個輸入變量存在最不利組合與最有利組合。其中有的輸出變量的最大值與均值的比值超過了1.1，應警惕最大值的出現。更科學的方法是采用一定置信度的置信區間來進行分析或設計。

(4)此外，同樣的計算模型，減少抽樣次數后輸出變量的變異系數出現一定程度的增大。在相同的抽樣次數下，將輸入變量的抽樣范圍擴大后輸出變量的變異系數出現較明顯的增大，且二者并非線性關系。因此，應盡可能地保證采空區充填效果達到或滿足設計要求，嚴格控制充填效果的變異程度以及變異范圍，從而使充填方案要達到的目標具有良好的可控性或穩定性。

［1］ 許家林，軒大洋，朱衛兵.充填采煤技術現狀與展望［J］.采礦技術，2011，11(3):24-30.

［2］ 鄧 建，邊 利，彭懷生.一種新的蒙特卡羅隨機有限元方法［J］. 中南大學學報:自然科學版，2006，37(5):997-1001.

［3］ 陳 虬，劉先斌.隨機有限元法及其工程應用［M］.成都:西南交通大學出版社，1993.

［4］ 李青鋒，王 戈，朱川曲.長壁工作面充填開采的充填比與充填效益分析［J］. 礦業工程研究，2009，24(2):21-24.

［5］ 樊志強，趙玉成，王繼燕.采空區充填前后巖層變形規律研究［J］. 煤炭工程，2011，(1):66-68.

［6］ 黃萬朋，馬樹坤，朱全美，陳明程.井下采空區部分充填參數的確定［J］. 煤礦安全，2011，42(7):150-152.

［7］ 李海清，向 龍，陳壽根.房柱式采空區受力分析及穩定性評價體系的建立［J］. 煤礦安全，2011，42(3):138-142.