從頭計算研究BCl+基態(tài)和激發(fā)態(tài)的勢能曲線和光譜性質(zhì)*

于坤1)2) 張曉美2) 劉玉芳2)?

1)(興義民族師范學(xué)院物理系，興義 562400)

2)(河南師范大學(xué)物理與電子工程學(xué)院，新鄉(xiāng) 453007)

(2012年10月29日收到;2012年11月19日收到修改稿)

1 引言

鹵代硼化物在半導(dǎo)體材料、金屬蝕刻和微電子器件制造等過程中起著非常重要的作用[1,2].由于鹵代硼化物與金屬表面相互作用的過程中會產(chǎn)生大量的中性BCl自由基以及它的陽離子BCl+，所以通過研究BCl和BCl+的物理化學(xué)性質(zhì)有助于人們理解鹵代硼化物在工業(yè)過程中的反應(yīng)機理.

BCl和BCl+在分子反應(yīng)中的物理化學(xué)性質(zhì)已經(jīng)引起了研究者的廣泛關(guān)注，許多研究者試圖通過研究它們的光譜特性和電子結(jié)構(gòu)來探究其在反應(yīng)過程中的重要作用[3-11].Hildenbrand[9]通過實驗確定了BCl+基態(tài)離解能為3.53 eV±0.11 eV.Bauschlicher和Ricca[10]進行了理論B3LYP/6-311+G(2df)級別的從頭計算確定了BFn，BF+n，BCln和BCl+n(n=1—3)的幾何結(jié)構(gòu)和振動頻率.Irikura等[11]通過從頭計算EE-EOM-CCSD方法結(jié)合相關(guān)一致aug-cc-pVTZ基組確定了BCl+基態(tài)的光譜參數(shù) Re，ωe，ωeχe.然而，對于 BCl+分子的電子結(jié)構(gòu)和光譜性質(zhì)，前人的工作僅僅局限于對BCl+基態(tài)的研究[9-11]，關(guān)于激發(fā)態(tài)的研究還未見報道.最近，雖然我們對BCl自由基的電子結(jié)構(gòu)進行了深入的研究[8]，但是對于BCl+激發(fā)態(tài)的勢能曲線和光譜性質(zhì)還未進行過研究.

本文利用了能夠充分考慮動力學(xué)相關(guān)的內(nèi)收縮多參考組態(tài)相互作用方法計算了BCl+自由基的基態(tài)和13個激發(fā)態(tài)的勢能曲線，為了得到更加準(zhǔn)確的勢能曲線，計算中考慮了Davidson矯正和標(biāo)量相對論修正以及BCl+自由基的4個Λ-S自旋軌道耦合效應(yīng).利用LEVEL8.0程序擬合了束縛Λ-S態(tài)和?態(tài)的光譜參數(shù)，并與已有的Λ-S態(tài)X2Σ+的實驗結(jié)果進行了對比，從而驗證了本文計算結(jié)果的可靠性.文中首次計算得到的數(shù)據(jù)不僅為實驗上研究BCl+復(fù)雜的光譜性質(zhì)提供了相關(guān)的電子結(jié)構(gòu)信息，而且也為相關(guān)體系的分子反應(yīng)動力學(xué)[12,13]研究提供了可靠的理論依據(jù).

2 計算方法

本文所有涉及BCl+自由基電子結(jié)構(gòu)的計算均使用了專業(yè)的量子化學(xué)Molpro程序2010.1版本[14].基于該程序計算得到的勢能曲線，使用LEVEL8.0程序[15]通過求解徑向的Schr¨odinger方程得到了束縛態(tài)的光譜參數(shù).

對于BCl+自由基，選取非收縮的高斯型全電子加彌散相關(guān)一致4zeta價基[aug-cc-pVQZ]作為B：13s7p4d3f2g和 Cl：17s12p4d3f2g的計算所用基組;選取步長為0.05?A，核間距0.8?A到6.0?A的105個點進行能量掃描.每個單點能的計算依次使用如下三步計算方法：首先，利用單組態(tài)的Hartree-Fock(RHF)方法計算了BCl+的基態(tài)X2Σ+，生成基態(tài)的波函數(shù);然后利用全活性空間自洽場方法(CASSCF)[16,17]對生成的基態(tài)波函數(shù)進行優(yōu)化;最后利用內(nèi)收縮多參考態(tài)相互作用方法(MRCI)[18,19]進行動力學(xué)相關(guān)能的計算進而得到相應(yīng)的勢能曲線，進一步提高勢能曲線的質(zhì)量.計算過程中還考慮了Davidson矯正(+Q)和標(biāo)量相對論效應(yīng).

由于MOLPRO程序自身的限制，計算中使用了C∞ν群的子群C2ν群.C2ν群擁有4個不可約表示，分別是 A1，B1，B2，A2.在計算過程中 BCl+自由基的9個軌道被選為活性空間，包括5個a1，2個b1和2個b2對稱性的分子軌道，它們對應(yīng)B原子的原子軌道2s2p和Cl原子的軌道3s3p.B+的外層電子2s2和Cl的外層電子3s23p5被放置在活性空間內(nèi)，剩下的12個電子被凍結(jié)而不進行相關(guān)能的計算.也就是說，在計算過程中，BCl+的9個電子參與了相關(guān)能的計算.

自旋軌道相互作用的研究[20,21]借助于MRCI+Q計算之后的全電子的Breit-Pauli哈密頓計算，計算中利用的是態(tài)相互作用，即通過在電子哈密頓本征函數(shù)基中對角化電子哈密頓本征函數(shù)和自旋軌道哈密頓本征函數(shù)之和獲得自旋軌道本征態(tài).其中哈密頓矩陣元Hel和HSO分別來自于MRCI+Q和CASSCF計算.自旋軌道相互作用使得BCl+自由基能量較低較為穩(wěn)定的4個Λ-S態(tài)分裂成為7個?態(tài)，隨后給出了相應(yīng)的?態(tài)的勢能曲線.

在計算得到Λ-S和?態(tài)的勢能曲線以后，通過求解徑向的核的Schr¨odinger方程得到了束縛態(tài)的光譜常數(shù)，包括離解能De，平衡核間距Re，激發(fā)能Te，振動常數(shù)ωe和ωeχe，平衡轉(zhuǎn)動常數(shù)Be.同時為了說明Λ-S電子態(tài)的多組態(tài)性質(zhì)，還給出了Re處主要的電子組態(tài)以及相應(yīng)的權(quán)重.通過分析這些電子組態(tài)還可以得到形成Λ-S態(tài)所滿足的躍遷規(guī)則.

3 結(jié)果與討論

3.1 Λ-S態(tài)的勢能曲線和光譜參數(shù)

利用多參考組態(tài)相互作用方法結(jié)合相關(guān)一致aug-cc-pVQZ基組計算得到了14個Λ-S態(tài)的勢能曲線，包括8個雙重態(tài)和6個四重態(tài)，這些態(tài)均為束縛態(tài).它們分別對應(yīng)兩個離解極限B+(1Sg)+Cl(2Pu)和B(2Pu)+Cl+(3Pg)，離解極限見表1，計算的MRCI+Q絕熱勢能曲線見圖1.利用LEVEL8.0程序?qū)κ`Λ-S態(tài)進行擬合得到的光譜參數(shù)列于表2，表2同時還給出了每個束縛態(tài)在平衡位置處主要的電子組態(tài)及相應(yīng)權(quán)重.

表1 BCl+自由基Λ-S態(tài)的離解極限

圖1 BCl+自由基的Λ-S態(tài)的勢能曲線 (a)二重態(tài);(b)四重態(tài)

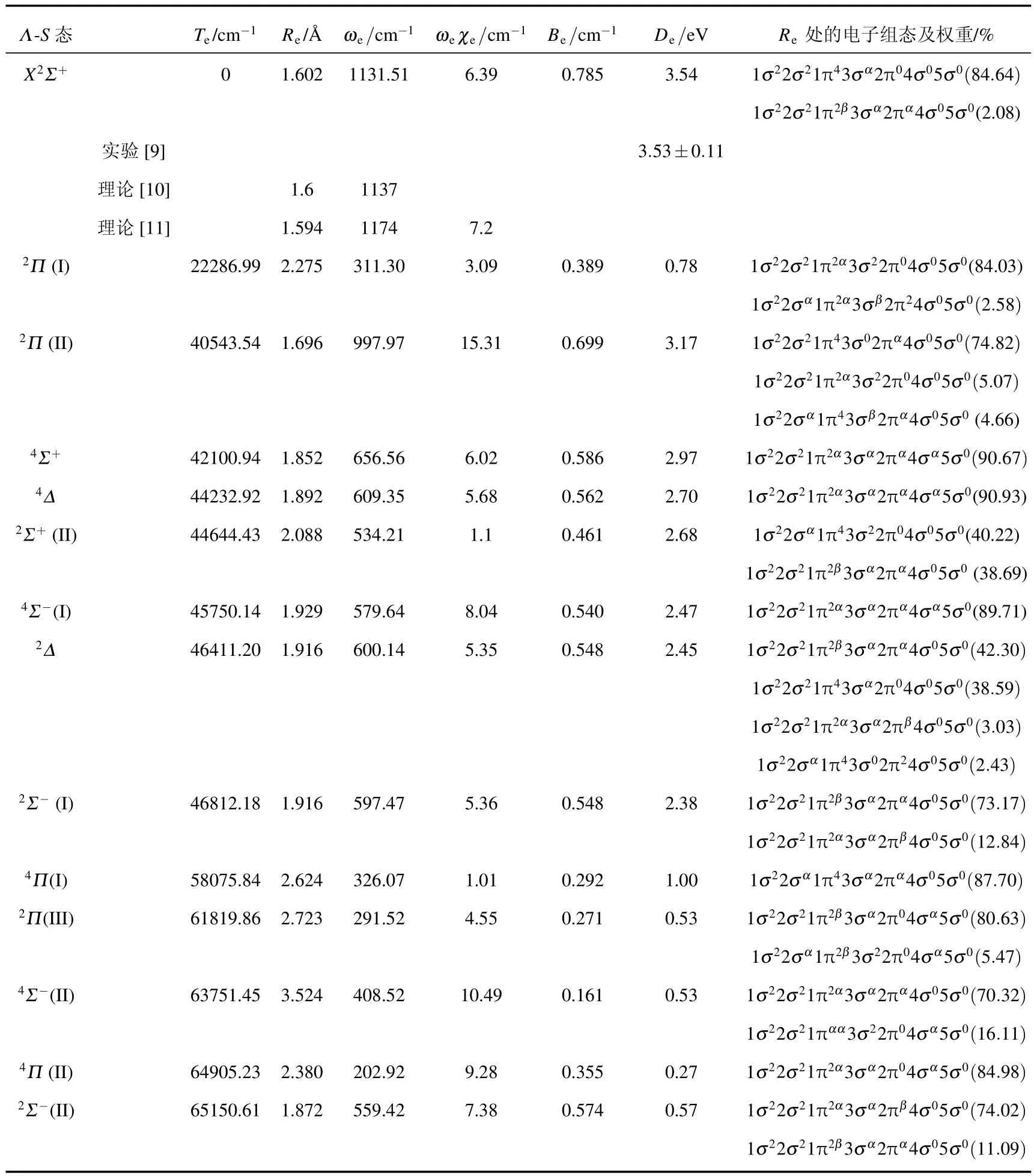
表2 BCl+自由基的Λ-S態(tài)的光譜參數(shù)

自由基BCl+的基態(tài)X2Σ+的主要組態(tài)是1σ22σ21π43σα2π04σ05σ0，是一個深勢阱的束縛態(tài)，其勢阱深度為3.54 eV，與Hildenbrand[9]實驗測到的BCl+的離解能值3.53 eV±0.11 eV非常符合.與文獻比較發(fā)現(xiàn)，我們計算的光譜參數(shù)與Bauschlicher和Ricca[10]的結(jié)果非常接近.平衡核間距的差別僅僅是0.002?A，振動常數(shù)ωe的差別也非常小，只有5.49 cm-1.在Irikura等[11]的理論計算結(jié)果中，Re值與我們的結(jié)果也很相符，但是ωe的值差別較大，非諧性常數(shù)ωeχe差別也較大.這可能是因為使用了cc-pVTZ基組考慮的相關(guān)能不足導(dǎo)致的. 和基態(tài)持有相同的離解極限B+(1Sg)+Cl(2Pu)的電子態(tài)還有第一激發(fā)態(tài)2Π(I).與基態(tài)相比2Π(I)是一個淺勢井的束縛態(tài)，深度僅僅有0.8 eV，平衡位置的電子結(jié)構(gòu)為1σ22σ21π2α3σ22π04σ05σ0，分析組態(tài)可以確定該態(tài)是基于基態(tài)的1π→3σ單電子激發(fā)形成的.文中2Π(I)態(tài)的光譜參數(shù)為首次報道，預(yù)測得到的電子態(tài)2Π(I)的能量最小值Te為22286.99 cm-1處于較大的核間距2.275?A的位置.計算的振動常數(shù)ωe和ωeχe分別為311.30和3.09 cm-1.

B原子基態(tài)2Pu和Cl+離子的基態(tài)3Pg通過相互作用可以形成6個雙重態(tài)和6個四重態(tài)，通過計算確定了它們之中能量最低的電子態(tài)為2Π(II)，激發(fā)能Te=40543.54 cm-1，在平衡位置處的電子結(jié)構(gòu)主要是 1σ22σ21π43σ02πα4σ05σ0.預(yù)測該態(tài)的離解能為3.1737 eV，表明該態(tài)的勢阱較深，說明BCl+自由基在參與化學(xué)反應(yīng)中處于該態(tài)的可能性較大.基態(tài)1π→2π的單電子激發(fā)可形成2Σ-(I)，2Σ-(II)和2Δ，其中2Σ-(I)和2Δ的勢能曲線幾乎完全重合.它們的平衡核間距Re相同，絕熱激發(fā)能Te也非常接近，分別為46812.18和46411.20 cm-1，振動常數(shù)ωe的差別也僅為2.67 cm-1.此外，從表1可以看出2Δ態(tài)的平衡位置處具有多個權(quán)重較大的電子組態(tài)，從而表明了采用多參考組態(tài)方法的必要性.2Π對稱性的第三個根2Π(III)是基于基態(tài)的1π→4σ電子激發(fā)形成的，具有較高的能量和較淺的勢阱，它的激發(fā)能Te=61819.86 cm-1，離解能De為0.53 eV.

與6個二重的Λ-S態(tài)對應(yīng)的是6個四重Λ-S態(tài)，它們之間的區(qū)別在于電子組態(tài)中電子的自旋排列方式不同，所以這些態(tài)形成的激發(fā)方式與二重態(tài)一致.在四重態(tài)中，能量最低的電子態(tài)為4Σ+，激發(fā)能為42100.94 cm-1，略高于2Π(II)的激發(fā)能40543.54 cm-1.值得注意的是它的勢能曲線與4Σ-(I)和4Δ的勢能曲線也非常靠近，所以它們的光譜參數(shù)比較接近.4Δ和4Σ-(I)的激發(fā)能為44232.92和45750.14 cm-1，三者的勢阱深度也相當(dāng)，分別是 2.97，2.70和 2.47 eV.其余三個 Λ-S 態(tài)4Σ-(II)，4Π(I)和4Π(II)的能量都比較高，激發(fā)能都集中在60000 cm-1附近，其中4Π(II)的能量最高，Te為64905.23 cm-1.而且4Π(II)存在一個不明顯的勢壘，位于鍵長3.14?A處，這個勢壘是由于4Π(II)與比它能量更高4Π對稱性的電子態(tài)之間的避免交叉而形成的，并且這個勢壘還導(dǎo)致了4Π(II)具有兩個勢阱，但由于這兩個勢阱都特別淺，很難在圖1中觀測到.表2中的光譜數(shù)據(jù)是通過擬合Re較小的那個勢阱得到的.

3.2 ?態(tài)的勢能曲線和光譜參數(shù)

在考慮旋軌耦合效應(yīng)的情況下，計算得到了7個?態(tài)的勢能曲線，包括4個1/2態(tài)和3個3/2態(tài).這7個?態(tài)對應(yīng)的原子基態(tài)的離解極限能量從低到高依次為：B+(1S0)+Cl(2P3/2)，B+(1S0)+Cl(2P1/2)和B(2P1/2)+Cl+(3P2).我們計算的Cl基態(tài)Cl(2P3/2)和第一激發(fā)態(tài)Cl(2P1/2)的能量差為910.57 cm-1，與相應(yīng)的實驗值882.35 cm-1比較接近.計算的?態(tài)的離解極限都列在了表3中，計算得到的?態(tài)勢能曲線見圖2，擬合的光譜參數(shù)以及Λ-S態(tài)組成成分列于表4.

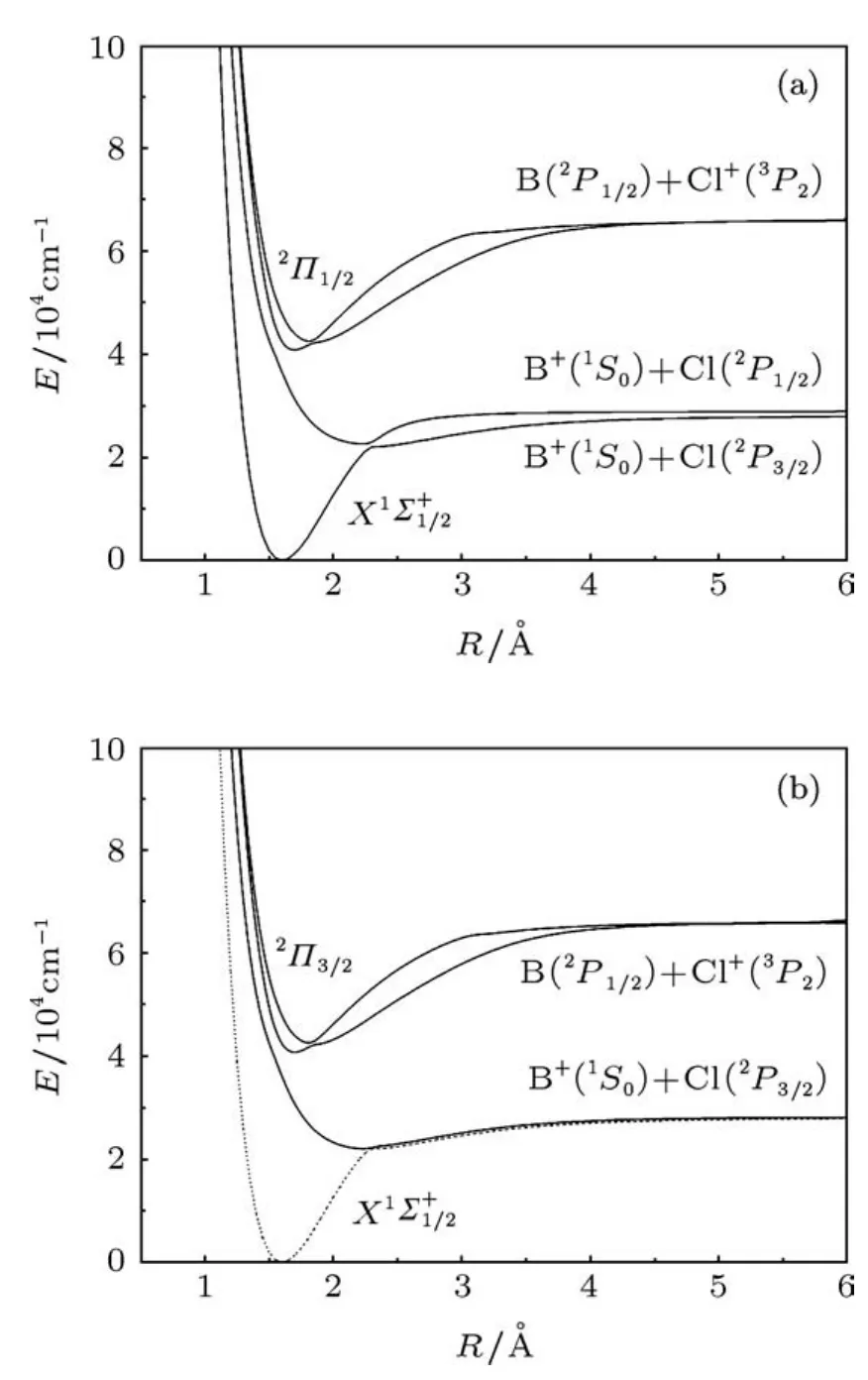
圖2 BCl+自由基的?態(tài)的勢能曲線 (a)?=1/2電子態(tài);(b)?=3/2電子態(tài)

基態(tài)?態(tài)為1/2態(tài)，在平衡位置處幾乎完全來自于X2Σ+態(tài)，考慮旋軌耦合效應(yīng)以后，基態(tài)的勢阱深度由原來的3.54 eV變?yōu)?.50 eV，其他的光譜參數(shù)幾乎沒有發(fā)生變化.對于第一激發(fā)態(tài)?=3/2(I)來說，在平衡位置幾乎完全來自2Π(I)態(tài)，其激發(fā)能Te為22014.40 cm-1位于鍵長2.241?A處，和2Π(I)的光譜參數(shù)都非常接近，勢阱深度與2Π(I)也幾乎相同.1/2對稱性的第二個根也為束縛態(tài)，其勢阱較淺，離解能De=0.79 eV，光譜參數(shù)同?=3/2態(tài)幾乎相同，在平衡位置處的Λ-S態(tài)成分以及權(quán)重分別為2Π(I)(92.6%)和X2Σ+(5.1%).在鍵長2.299?A處，其勢能曲線與基態(tài)的1/2態(tài)的勢能曲線存在非常明顯的避免交叉，這是由于考慮了旋軌耦合效應(yīng)引起的.

表3 BCl+自由基?態(tài)的離解極限

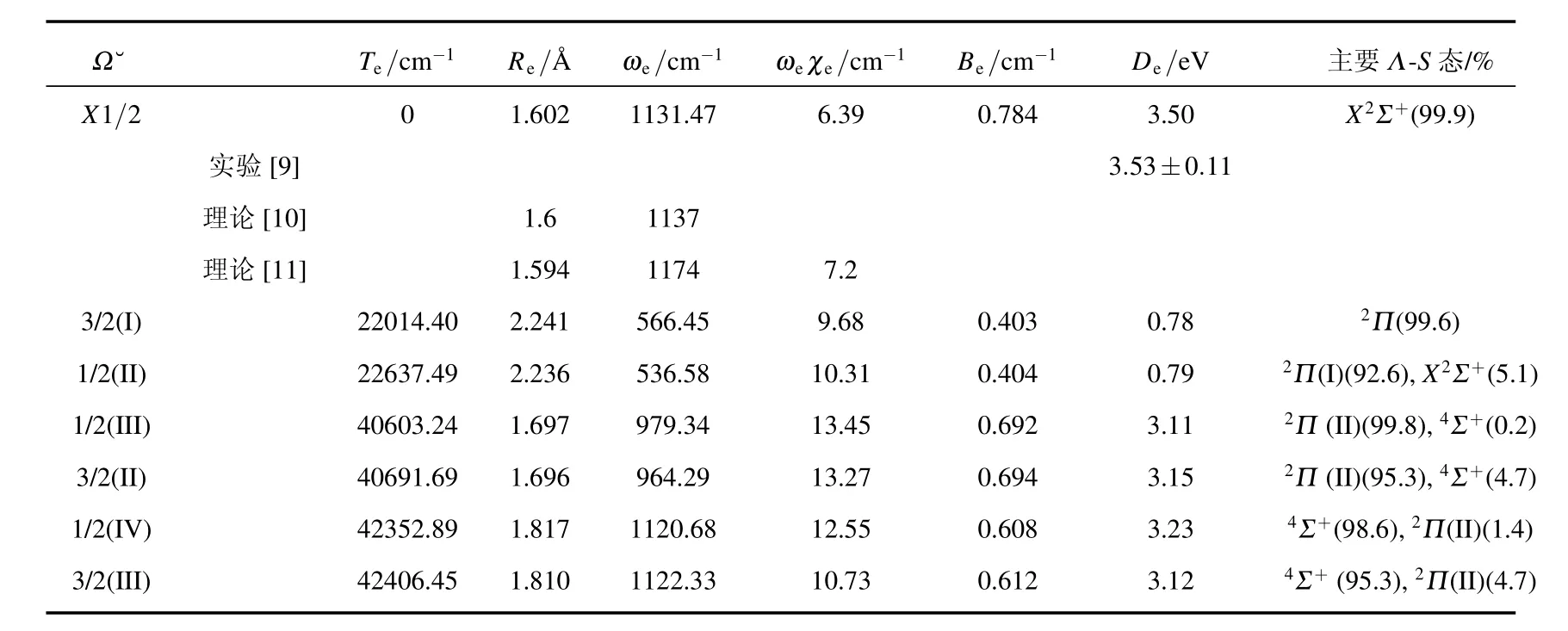
表4 BCl+自由基的?態(tài)的光譜參數(shù)

另外四個?態(tài)包括2個3/2態(tài)和2個1/2態(tài)，它們對應(yīng)相同的離解極限B(2P1/2)+Cl+(3P2)，勢阱都較淺.?態(tài)1/2(III)和3/2(II)主要是通過2Π(II)分裂形成的，由于自旋軌道相互作用較弱，在計算中被視為微擾，故這兩個?態(tài)的激發(fā)能差別很小，計算得到的激發(fā)能Te差別只有88.45 cm-1，其余的光譜參數(shù)也很接近.4Σ+分裂形成了兩個?態(tài) 1/2(IV)和 3/2(III)，它們的情況與 1/2(III)和3/2(II)類似，這里不再贅述.值得指出的是1/2(III)和1/2(IV)，3/2(II)和3/2(III)的勢能曲線分別出現(xiàn)了明顯的避免交叉(見圖2)，這同樣是由于考慮了自旋軌道相互作用引起的.

4 總結(jié)

本文利用了考慮標(biāo)量相對論效應(yīng)的多參考組態(tài)相互作用方法(MRCI+Q)和相關(guān)一致極化價基aug-cc-pVQZ計算了0.8—6.0?A核間距范圍的14個Λ-S態(tài)的勢能曲線，獲得的14個Λ-S態(tài)分別對應(yīng)兩個離解極限B+(1Sg)+Cl(2Pu)和B(2Pu)+Cl+(3Pg).旋軌耦合效應(yīng)使得能量最低的4個ΛS態(tài)分裂成了7個?態(tài)，并導(dǎo)致?態(tài)的勢能曲線產(chǎn)生了非常明顯的避免交叉.通過求解徑向的Schr¨odinger方程得到了Λ-S態(tài)和?態(tài)的光譜參數(shù).計算得到Λ-S態(tài)的基態(tài)結(jié)果與實驗符合得非常好.值得注意的是，除基態(tài)外，其余13個Λ-S態(tài)和?態(tài)的光譜常數(shù)均為首次報道.此外，本文還給出了每個Λ-S態(tài)的電子結(jié)構(gòu)性質(zhì)，通過分析它們的電子結(jié)構(gòu)特性，我們得到了各態(tài)的電子躍遷特性.同時，所給出的束縛態(tài)主要組態(tài)和權(quán)重也體現(xiàn)出了這些電子態(tài)的多組態(tài)性質(zhì)，表明了使用多參考態(tài)方法的必要性.本文的計算結(jié)果為實驗上研究BCl+復(fù)雜的光譜性質(zhì)提供了一定的理論依據(jù)和參考.

[1]Flamm D L 1993Solid State Technol.36 49

[2]Patron S J，Hobson W S，Abernathy C R，Ren F，F(xiàn)ullowan T R，Katz A，Perle A P 1993Plasma Chem.Plasma Proc.13 311

[3]Huber K P，Herzberg G 1979Molecular Spectra and Molecular Structure IV:Constants of Diatomic Molecules(New York：VanNostrand Reinhold)

[4]Maki A G，Lovas F J，Suenram R D 1982 J.Mol.Spectrosc.91 424

[5]Bredohl H，Dubois I，Houbrechts Y，Nzohabonayo P 1984 J.Phys.B：At.Mol.Phys.17 209

[6]Bredohl H，Dubois I，M′elen F 1987 J.Mol.Spectrosc.121 135

[7]Verma R D 1995 J.Mol.Spectrosc.169 295

[8]Liu Y F，Zhang X M，Yu K 2012 Computat.Theor.Chem.991 82

[9]Hildenbrand D L 1996 J.Chem.Phys.105 10507

[10]Bauschlicher C W，Ricca A 1999 J.Phys.Chem.A 103 4313

[11]Irikura K K，Johnson R D，Hudgens J W 2000 J.Phys.Chem.A 104 3800

[12]Wang X Y，Ding S L 2004 Acta Phys.Sin.53 423(in Chinese)[王曉艷，丁世良2004物理學(xué)報53 423]

[13]Han H X，Peng Q，Wen Z Y，Wang Y B 2005 Acta Phys.Sin.54 78(in Chinese)[韓慧仙，彭謙，文振翼，王育彬2005物理學(xué)報54 78]

[14]Werner H J，Knowles P J，Lindh R.Manby F R，Sch¨utz M，Celani P，Korona T，Rauhut G，Amos R D，Bernhardsson A http：//www.molpro.net.[2012-10-29]

[15]Le Roy R J 2007 LEVEL 8.0:A Computer Program for Solving the Radial Schr¨odinger Equation for Bound and Quasibound Levels.University of Waterloo Chemical Physics Research Report CP-663

[16]Werner H J，Knowles P J 1985 J.Chem.Phys.82 5053

[17]Knowles P J，Werner H J 1985 Chem.Phys.Lett.115 259

[18]Werner H J，Knowles P J 1988 J.Chem.Phys.89 5803

[19]Knowles P J，Werner H J 1988 Chem.Phys.Lett.145 514

[20]Yan B，Pan S F，Wang Z G，Yu J H 2005 Acta Phys.Sin.54 5618(in Chinese)[閆冰，潘守甫，王志剛，于俊華2005物理學(xué)報54 5618]

[21]Li R，Lian K Y，Li Q N，Miao F J，Yan Bing，Jin M X 2012 Chin.Phys.B 21 123102

[22]Moore C E 1971 Atomic Energy Levels(Washington，DC：National Bureau of Standards)