公交發車間隔模型研究＊

李發智 肖 蕾 楊東援

（同濟大學教育部道路與交通工程重點實驗室1） 上海 201804） （西南交通大學交通運輸與物流學院2） 成都 610031）

0 引 言

目前，國內外學者對公交調度展開了大量的研究，大多都以乘客乘車成本最小化和公交公司收益最大化為目標進行調度時刻表優化.陳芳［1］在發車間隔的研究中以乘客等待時間和公交車運行費用為目標，通過權重法結合兩目標，分時段建立調度時刻優化模型，采用步長法進行仿真求解.張無非等［2］從原始數據處理到公交調度模型求解進行了研究.他們直觀地從車站客流變化入手，以乘客的等待時間和公交公司的利益為目標進行優化，然后求得發車間隔.在模型建立中，對乘客等待時間量化引入罰函數機制，避免乘客等待時間過長.戴連貴等［3］分時段考慮發車間隔優化，比較詳細地將乘客時間價值分成2部分：（1）乘客在車站的停留時間；（2）乘客的乘車時間.其中乘車時間又包括2站間的行駛時間、乘客下車時間、車上乘客停站等待時間.孫文霞等［4］假設公交車單位時間運營成本固定，認為乘客費用包括2部分：（1）在公車上的擁擠費用；（2）等車費用，且單位運費固定，建立公交調度模型，運用解析法求解.Andrede和Robin［5］將公交調度看成N中位問題，運用選址理論，分別考慮線性模型和環模型.朱金壽等［6］以小時為時段建立公交發車間隔模型，并設計求解算法.楊海軍等提出了一種旨在快速響應乘客出行需求的“小粒度”頻繁調度方法，構建了以“小粒度”時段為調度周期的多目標優化模型［7］.本文將公交線路處理成只有首末站的兩點間運輸，將中間站客流變化規律平移到首站，按照客流屬性進行時段劃分，以乘客的等車時間最小化和車輛的載客率最大化為目標，建立公交調度模型.

1 模型假設和符號系統

1.1 模型假設

1）公交線路上只有2個站，即首末站.實際中的公交線路還有一定數量的中間站，本文將中間站的客流處理到起點站，詳見客流特征提取部分.

2）公交運營以乘客利益為主要目標，同時兼顧資源（在此主要指車輛）的利用率（滿載率）.由于公共交通具有屬準公共物品，具有很強的社會公益性，且其外部效應遠遠高于公交內部收益，同時，國家和地方財政給予公交一定的支持，所以，本文以乘客時間成本最小化為目標.另外，資源的合理配置利用是公交面臨的又一棘手問題，所以本文以公交車輛載客率為目標.

3）車輛能承載候車的所有乘客.城市公交的發車頻率大，后一輛車基本上能承載前后兩輛車的時間間隙內達到的所有乘客.

1.2 符號系統

2 客流特性提取

本文考慮單條公交線路的調度問題.通過調查可獲得每個站點在各個時刻的上下客人數.第i車輛到達第j個公交車站的時間是，整條公交線路有M個公交車站，在調查日的發車次數為N次.則到達站臺j的公交車時刻表為…，并且有的時間間隔為，上車的人數為），乘客到達率）為

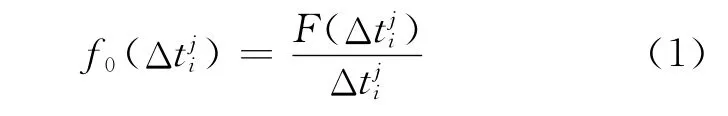
三次樣條是工業生產中應用較廣的插值方法，該方法可以得到平滑并且二階可導的曲線，但由于三次樣條插值要求樣條曲線必須經過樣本點，這使得因樣本數值的變化而曲線發生劇烈變化.所以，在此用平滑樣條（有理B樣條）來處理乘客到達率，平滑樣條得到的曲線較為平緩，并且并非必須經過樣本點.根據常州市B22公交線路2010年6月11日的調查數據，擬合得到站點乘客到達率曲線，見圖1.

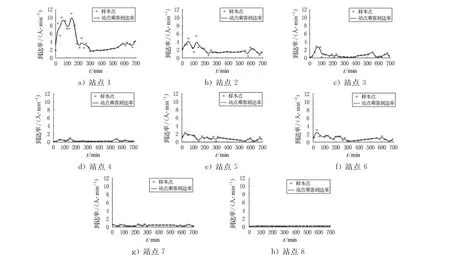
圖1 各站（站1到站8）乘客到達率曲線

公交首站（第1站）到站j的運行時間為tj0，則時間t在站點j的乘客乘坐車次在首站發車時刻為t－tj0（見表1和圖2）.通過平移時間tj0，將站點j的乘客到達率轉換為首站乘客到達率，當把所有的中間站乘客到達率都平移到首站，則線路的乘客到達率即為首站的乘客到達率，達到率表達式為

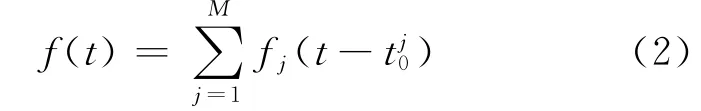
表1 各站運行時間間隔

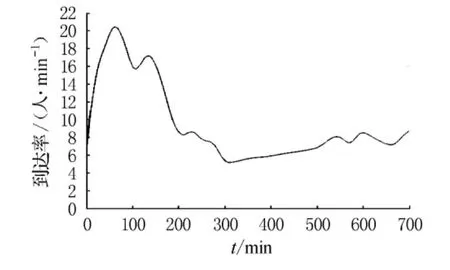
圖2 公交線路乘客到達率

3 調度時段劃分

以步長為Δl為時間刻度（比如10min）將一天內的發車總時長等分，則有刻度0，Δl，2Δl，…，kΔl，…，KΔl，T.其中：0為首班車發車時間，T 為末班車的發車時間，K＝［T／Δl］為下取整，聚類中不考慮首末班車，將其合并到第一個和最后時段.則有中間時刻對應的乘客到達率為

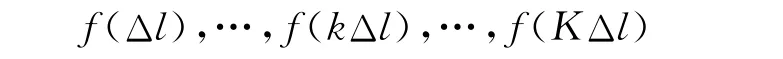
各時刻的乘客到達率組成一維有序樣本.為了方便，將f（kΔl）簡化為fk.按照某一劃分規則，將其劃分為 P（K，s）：｛fi1，fi1＋1，…，fi2－1｝，｛fi2，fi2＋1，…，fi3－1｝，…，｛fis，fis＋1，…，fK｝.其中：1＝i1＜i2＜…＜is＜K.

定義1 類｛fi，fi＋1，…，fj－1｝的相似度S（i）

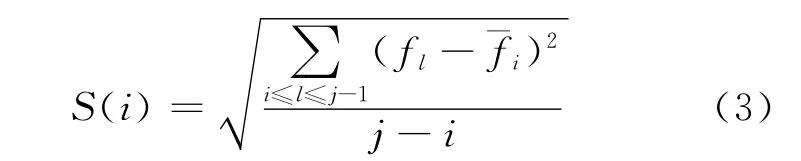
定義2 相鄰2類｛fi，fi＋1，…，fj－1｝，｛fj，fj＋1，…，fj－1｝的距離

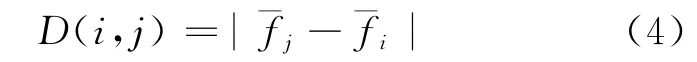
由定義可見，D（i，j）越大，類之間的差異性越顯著.

定義3 分類P（K，s）的誤差函數

式（7）表示分類數不得少于s0，s0為常數，取2.

根據聚類優化模型，將該公交線路的客流達到曲線數據聚成5類為最優結果（見表2和圖3）.

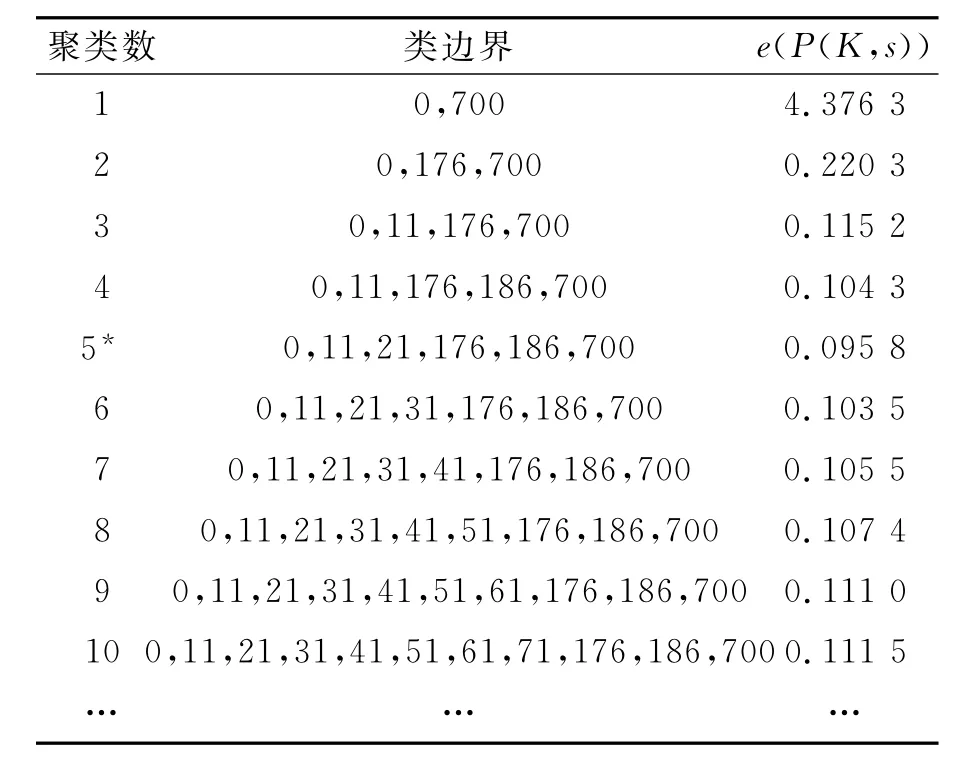
表2 聚類結果

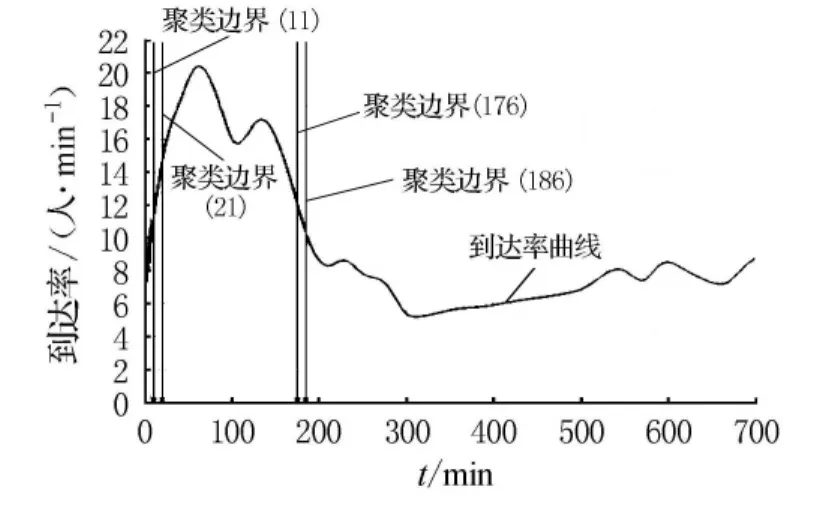
圖3 聚類結果圖

4 公交調度模型

基于調度時段劃分，該部分的公交調度模型，只對某一時段［Ta，Tb］進行分析即可.設定發車間隔為Δt，則發車時刻為Ta＋Δt，Ta＝2Δt，…，Ta＋NΔt，其中，Nab為該區段的發車總數，Nab＝［（Tb－Ta）／Δt］.發車間隔內到站的乘客數Fi為

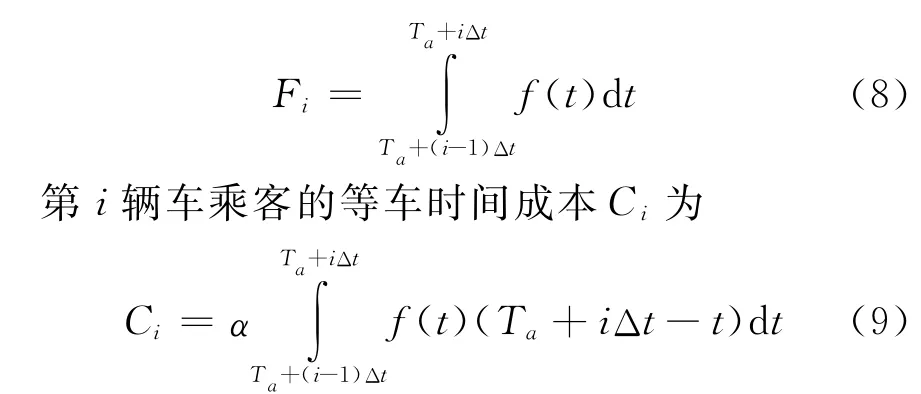
式中：α為時間價值系數.時間價值系數即時間價值成本，包括隱性成本和顯性成本.隱性成本是指因時間延誤造成的隱性損失，如公司的遲到處罰，體現形式為罰款、獎金折扣等.顯性成本指時間延誤的直接損失，如不能按時到崗的生產力損失，體現形式為工資損失等.在此簡化處理，隱性成本按30元／min計量，顯性成本根據平均工資計算為0.28元／min（＝3 000／（22×8×60）），設定有隱性成本的乘客比例為4%，時間價值期望α為1.47元／min（＝30×4%＋0.28×96%）.

車輛的載客率定義為最大斷面車內人數與最大荷載之比.當將公交線路簡化成僅有首末站時，其車內人數即為最大斷面載客數量，然而實際情況是在中途各站均有上下客，所以最大斷面載客數小于發車間隔內的乘車人數，在此用第i輛車的折算系數λi進行處理.折算系數可以通過調查客流數據統計得到.在同一調度時段內，不同車次的折算系數變化較小，可視為常數λ.即有

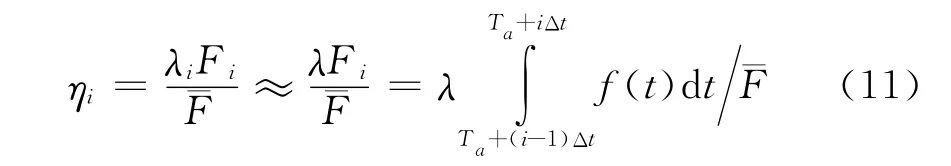
式中：ˉF為公交車的最大荷載量；λi，λ為折算系數.

整個調度時段的平均載客率為

其中：式（13）以乘客候車時間最小化為目標；式（14）以車輛的平均載客率最大化為目標；約束（15）為發車間隔區間約束，高峰時段為［2min，10min］，平峰時段為［5min，30min］，若既有高峰時段，又有平峰時段的區間，該約束區間為［2min，30min］.見表3.

該模型是一個多目標規劃，為了便于求解，將多目標化為單目標.將目標（14）劃成如下約束

式中：η0為載客率下限，平峰時段一般取60%，高峰時段取80%.

根據第三部分的聚類結果，求解區間［21，176］內的發車間隔.該區間對應的時段是［06：51，09：26］，為高峰時段，發車時刻約束［Δt′0，Δt″0］為［2min，10min］.根據實際情況，相關參數取值為：ˉF，100人；α，1.47元／min；λ，0.8；η0，80%.經模型計算，最優發車時間間隔為6min.見表3、表4.

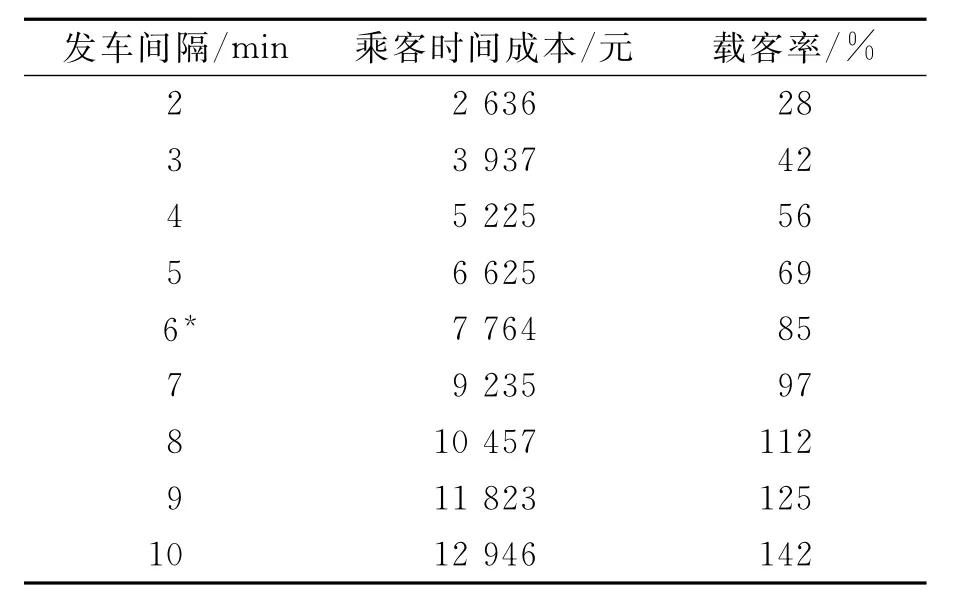
表3 計算結果

表4 發車時刻表

5 結束語

本文以常州公交線路B22跟車調查數據為支撐，建立了一套確定發車時刻表的方法.該方法分為3步驟：（1）擬合乘客到達率曲線，采用時間平移將中間站的客流特征轉化到公交首站，簡化了調度模型建立過程；（2）結合Fisher有序樣本聚類思想，建立劃分調度時段的優化模型，劃分調度時段；（3）結合前2部的成果，綜合考慮乘客等車時間成本和車輛的利用率，確定發車間隔.全文以實證研究為主，整套方法簡潔地計算出發車時刻表，經調查數據驗證了模型和方法的可行性和實用性.

［1］陳 芳.城市公交調度模型研究［J］.中南公路工程，2005，30（2）：162－164.

［2］張無非，張 馳，嚴奇琦.對于公交汽車調度問題的求解［J］.工程數學學報，2002，19（S1）：81－88.

［3］戴連貴，劉正東.公交調度發車間隔多目標組合優化模型［J］.交通運輸系統工程與信息，2007（4）：43－46.

［4］孫文霞，宋 倜，喬國會.公交調度中發車間隔控制研究［J］.河北工業大學學報，2007，36（2）：89－93.

［5］ANDREDE P，ROBIN L.Optimal timetables for public transportation［J］.Transportation Research Part B－Methodological，2001，35（8）：789－813.

［6］朱金壽，朱 琪，楊勇剛，等.公交車調度方案的研究［J］.武漢理工大學學報：交通科學與工程版，2002，26（2）：169－171.

［7］楊海軍，賀國光.基于快速需求響應的城市公交在線調度方法研究［J］.武漢理工大學學報：交通科學與工程版，2009，33（3）：430－433.