混堆模式下集裝箱堆場箱區指派優化方法＊

鄭紅星 王曉薇 董 鍵 周汀洋

（大連海事大學交通運輸管理學院 大連 116026）

集裝箱堆場空間資源的調度直接影響碼頭前沿和堆場內裝卸資源的作業效率，以及裝卸設備的作業成本.P.Peter等［1］以船舶停港時間最短為目標，建立了集裝箱堆場最優堆存方案的混合整數線性規劃模型.Chen等［2］對集裝箱堆場空間分配問題進行研究，提出一種混合算法進行求解.Zhang［3］通過建立線性整數規劃模型對堆場空間進行分配，得到分配到各箱區的集裝箱數量.徐德磊［4］等根據箱區容量建立了集裝箱運輸最短路徑的集裝箱堆存分派模型.王斌［5－6］研究了混堆模式下堆場空間分配問題，并分別以平衡箱區箱量和最小化集卡行駛距離為目標，建立了兩階段決策模型；陶經輝等［7］提出了兩階段模型，并運用啟發式算法進行求解；徐亞等［8］建立了多目標規劃模型，并提出了一種改進的線性功效系數法進行求解.本文考慮到作業效率與堆存策略之間的聯系，以及堆場作業的連續性和動態變化性，建立堆場箱區資源均衡調度模型，合理分配各箱區的作業量.

1 箱區間資源均衡優化模型

1.1 問題描述

堆場中的集裝箱按其狀態，可分為5種類型：進口箱（discharge），簡稱D型箱，指尚在船上等待卸船的進口箱，被內部集卡運到堆場堆存；出口箱（loading），簡稱L型箱，指已在堆場上等待裝船的出口箱，被內部集卡運到岸橋邊裝船；中轉箱（transhipment），簡稱T型箱，指尚在某船上等待卸船被內部集卡運進堆場后，或者已經被運進堆場，等待內部集卡運到另一船出口的集裝箱；提箱（pickup），簡稱P型箱，指已經在堆場，等待外部集卡提走的進口箱；進箱（sending），簡稱S型箱，指尚未分配到堆場的出口箱，等待被外部集卡運進堆場堆存.當D型箱堆存到堆場后就變為P型箱，S型箱進入堆場后就變為L型箱.其中，T型箱在進出口碼頭作業中，其所占的比例較低，而且一般將該箱型單獨存放在一個箱區，文中對此種箱型不作考慮.因此，堆場箱型可簡化分成上述4種類型，基于這4種類型的集裝箱數量來對堆場空間資源進行分配.

由于集裝箱碼頭通常是24h連續作業，一般采用滾動模式安排作業調度計劃.運用滾動計劃模式需要一個固定時段作為計劃期，在計劃期內按照更新信息進行計劃安排，考慮到大多數碼頭的作業情況，本文以3d為一個計劃期，以12h為一個計劃時段，每天分為2個時段，則3d劃分為6個時段.每次決策一個計劃期內堆場空間資源調度情況，在這3d的計劃期中，初始時，只實施第1d的調度計劃，后2d的調度計劃編入到下一個計劃期，在下一個計劃期內重新制定計劃，以此類推.集裝箱碼頭滾動計劃模式見圖1.

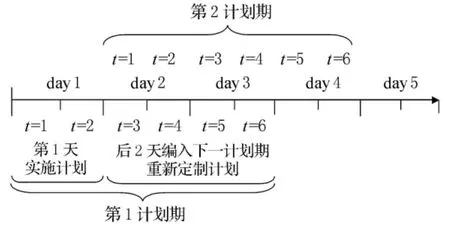
圖1 集裝箱碼頭滾動計劃模式圖

本文擬建立混堆模式下堆場箱區間作業量均衡優化模型，合理調配各箱區中4種箱型的作業量，使各箱區的作業量處于均衡狀態，從一定程度上提高裝卸設備的作業效率.

1.2 模型的建立

1.2.1 模型的假設條件 根據碼頭實際作業狀況，對部分指標或作業標準建立合理假設：（1）計劃期內，按照班輪作業計劃，船舶靠離泊位的時間為已知；（2）計劃期內，各船舶及港口出口集裝箱箱型、箱量、集裝箱重量等級為已知；（3）計劃期內，堆場后方陸側系統作業的出口箱運入堆場數量、進口箱的提箱數量及其作業時間為已知（可根據歷史統計數據得到）；（4）為了簡化模型，設定集裝箱堆場集裝箱型都為TEU標準.

1.2.2 模型的符號說明 M為堆場中的箱區總數；T為一個計劃期內的總時段數；i為堆場中的箱區編號（i∈［1，M］）；t為一個計劃周期內第t個計劃時段（t∈［1，T］）；Ci為箱區i的堆存容量；Dit為計劃時段t內卸到箱區i中的D型箱量；為計劃時段t內卸到箱區i中，在計劃期外被客戶提走的D型箱量；Dith為計劃時段t內卸到箱區i中，在計劃期內的h時段被客戶提走的D型箱量（h∈［t，T］）；Lit為計劃時段t內從箱區i提上船的L型箱量；為計劃期開始時已經在堆場的箱區i中，在計劃時段t內提上船的L型箱量；Ligt為計劃時段g內到港分配到箱區i中，在計劃時段t內提上船的L型箱量（g∈［1，t］）；Sit為計劃時段t內到港分配到箱區i中的S型箱量；~Sit為計劃時段t內到港分配到箱區i中，在計劃期外提上船的S型箱量；Sitk為計劃時段t內到港分配到箱區i中，在計劃時段k內提上船的S型箱量（k∈［t，T］）；Pit為計劃時段t內被客戶從箱區i中提走的P型箱量；為計劃期開始時已經在堆場的箱區i中，在計劃時段t內被客戶提走的P型箱量；Pilt為在計劃時段l內卸到箱區i中，在計劃時段t被客戶提走的P型箱量（l∈［1，t］）；Vi0為計劃時段開始時堆存在箱區i中的箱量；Vit為計劃時段t結束時堆存在箱區i中箱量.

1.2.3 目標函數 多目標資源均衡優化模型的目標函數為：min［μ1·f1＋μ2·f2］.式中：μ1為船舶裝卸計劃在各箱區作業量的均衡權重系數；μ2為整個堆場箱區作業量均衡權重系數，μ1＋μ2＝1.

目標函數1：船舶裝卸計劃在各箱區作業總量均衡.該目標可轉化為在計劃期內，船舶在各箱區i作業量的平均差為最小，即

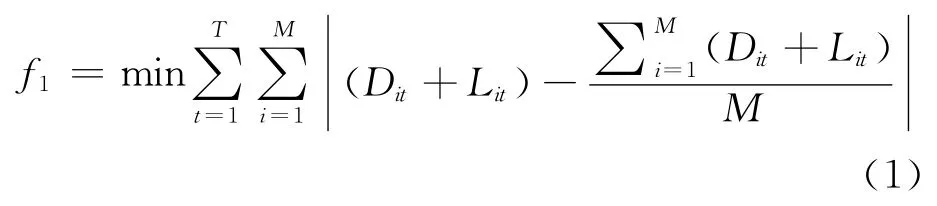
目標函數2：整個集裝箱堆場箱區作業總量均衡.該目標可轉化為在計劃期內，碼頭堆場的全部箱區中，各箱區作業量的平均差為最小，即

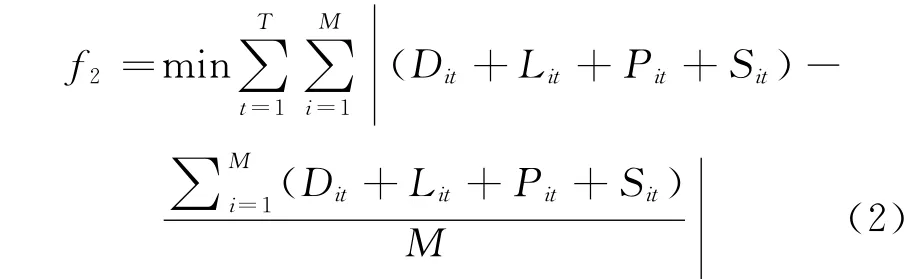
1.2.4 約束條件

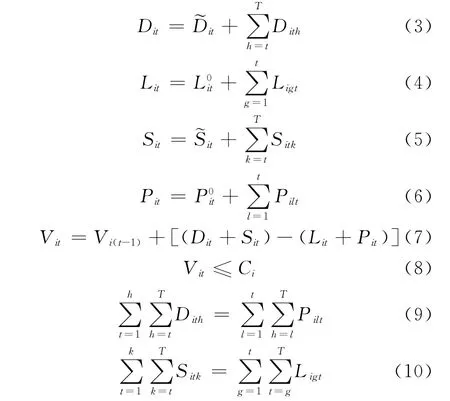
式中：Dit，Lit，Pit，Sit，Vit，i，t，h，g，k，l均為非負整數.

約束（3）保證計劃時段t內卸到箱區i中的D型箱總量等于計劃時段t內卸到箱區i中，在計劃期外被客戶提走的D型箱量與在計劃期內被客戶提走的D型箱總量之和；約束（4）保證計劃時段t內從箱區i提上船的L型箱量，等于計劃期開始時已經在堆場上的箱區i中t時段被提上船的L型箱量與計劃時段g內到港分配到箱區i中，在計劃時段t被提上船的L型箱量之和；約束（5）保證計劃時段t內到港分配到箱區i中的S型箱總量等于計劃時段t內到港分配到箱區i中，在計劃期外被提上船的S型箱量與在計劃期內被提上船的S型箱總量之和；約束（6）保證計劃時段t內被客戶從箱區i中提走的P型箱量，等于計劃期開始時已經在堆場上的箱區i中，在t時段被客戶提走的P型箱量與各船舶在計劃時段l內卸到箱區i中，在t時段被港外客戶提走的P型箱量之和；約束（7）表示箱區前后時段堆存數量的關系；約束（8）保證計劃期內各箱區集裝箱總量不能超過其堆存容量；約束（9）、（10）表示2箱型之間的關系；約束（11）保證各決策變量均為非負整數.

2 模型的求解

2.1 解的形式

模型中的決策變量為：計劃時段t內卸到箱區i中，計劃期外被提走的D型箱總量~Dit；計劃時段t內卸到箱區i中，計劃時段內被提走的D型箱總量；計劃時段t內送到箱區i中，計劃期外被提上船的S型箱總量~Sit；計劃時段t內送到箱區中，計劃時段內被提上船的S型箱總量.以上述決策變量為行，以所有箱區編號i（i＝1，2，…，10）為列，構造各個時段t（i＝1，2，…，6）對應下的解矩陣 Ax（x 為矩陣的編號），矩陣Ax為解的表現形式.

2.2 初始解的產生步驟

步驟2 i＝1，轉步驟3.

步驟5 i＝i＋1，判斷i的值，如果i＞M 轉步驟6；否則轉步驟3.

步驟6 t＝t＋1，判斷t的值，如果t＞6解的生成結束；否則轉步驟2.

2.3 新解的產生步驟

步驟1 獲取當前解Ax，轉步驟2.

步驟2 t＝1，轉步驟3.

步驟4 t＝t＋1，判斷t的值，如果t＞6，則新解生成結束；否則，轉步驟3，繼續循環.

2.4 適應度函數

以堆場箱區間空間資源調度模型的目標函數，作為算法的適應度函數：E（Ax）＝式中：μ1，μ2的值根據港口具體情況而定.

2.5 接受準則

按照模擬退火算法的原理，新解被接受的概率Cx1x2為

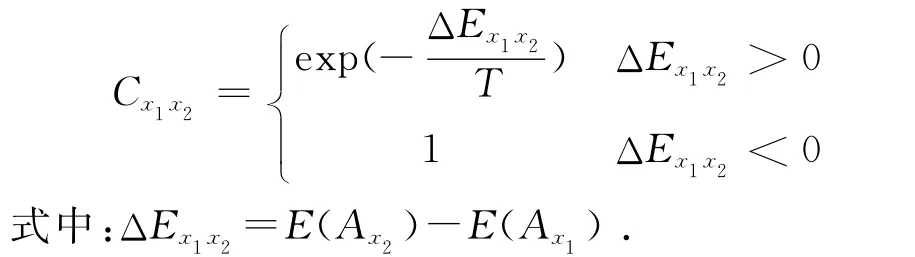
2.6 終止條件

循環終止條件為達到預定溫度，當算法達到預定的溫度時，當前解即為模型的優化解.

3 實例分析

3.1 初始數據

本案例來源于某港口實際運營數據，經簡化處理后有2個泊位，堆場箱區總數Z＝10，每個箱區共15個貝位，每個貝位分6排；最多堆垛層高為4層，其中第一排最大堆垛層高為2層，第二排最大堆垛層高為3層，每個箱區存儲容量Ci＝315TEU.

某計劃期內到港船舶數J＝3（艘），每艘船載箱量為200TEU.船舶1在t＝1時段開始卸船，在t＝3時段開始裝船；船舶2在t＝2時段開始卸船，在t＝4時段開始裝船；船舶3在t＝4時段開始卸船，在t＝6時段開始裝船.根據港口實際情況，船舶作業箱量在各箱區作業量均衡權重系數μ1＝0.7.本模型計劃期為3d，時段總數T＝6.

表1 的值

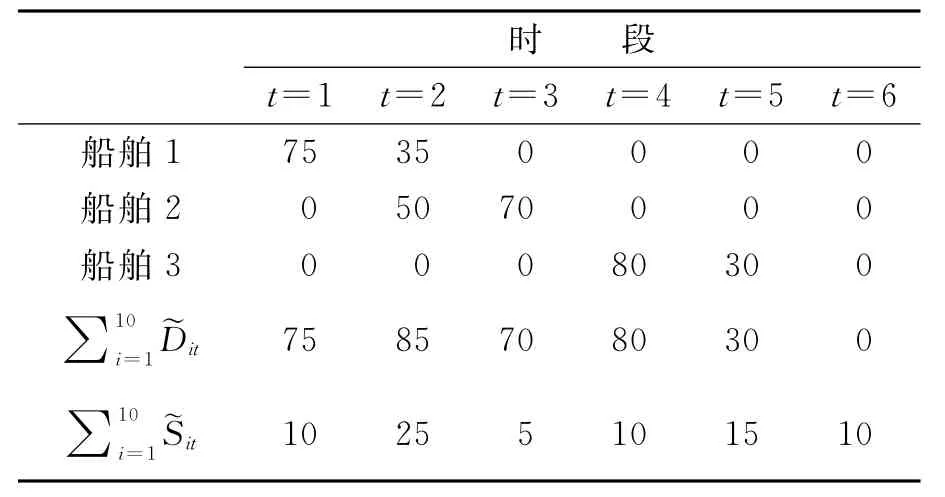
表1 的值

?

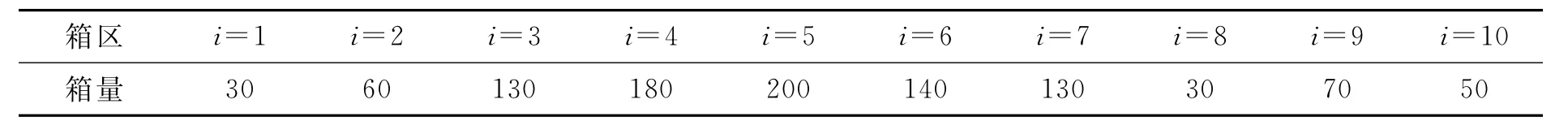
表2 初始計劃時段各箱區箱量Vi0

表3 的值

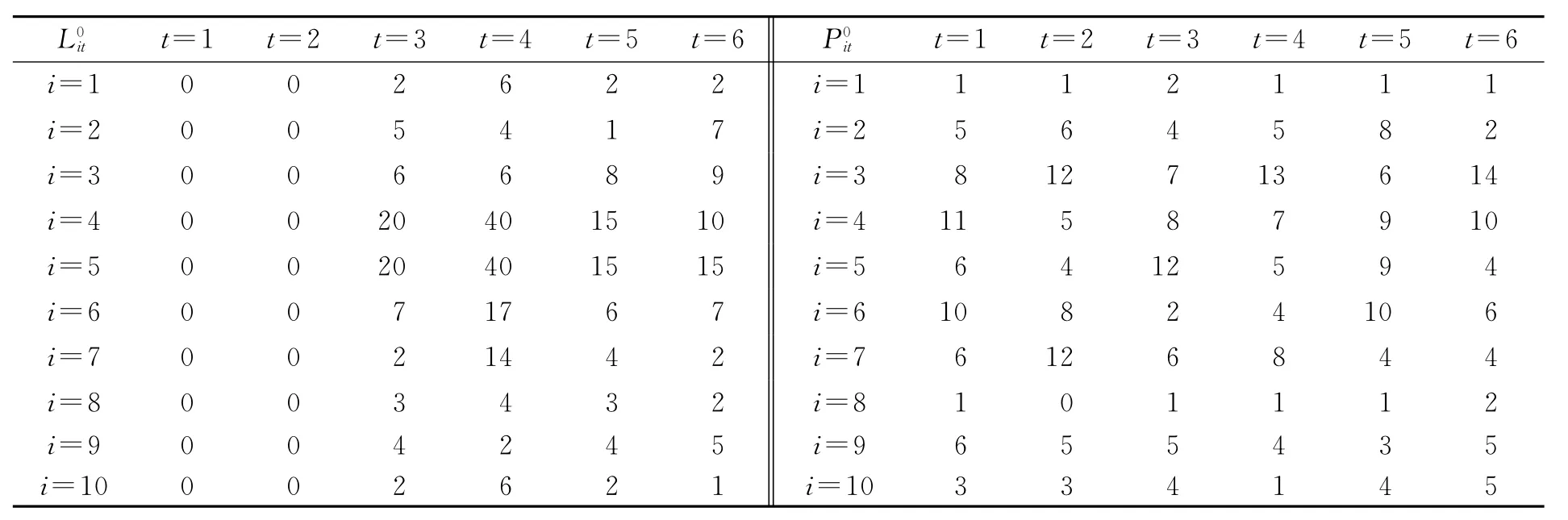
表3 的值

?

3.2 優化結果與分析

利用本研究建立的箱區間資源均衡優化模型的模擬退火算法，采用MATLAB語言進行編程，運用 Window7操作系統的Pentium（R）T4200處理器的PC機進行運算.

主要參數設置：初始溫度t0＝97，預訂溫度tf＝3，馬爾科夫鏈長度為500，降溫系數為0.94；矩陣DS各行從上到下依次為的值；矩陣L0表示的值；矩陣L表示的值；矩陣P0表示的值；矩陣P表示的值；矩陣ini＿vol表示計劃初始時段各箱區的箱量.利用上述等參數來控制程序運算，目標函數值趨向收斂，目標函數收斂圖見圖2，各箱型在各時段分配到各箱區的箱量見表4，得出總的均衡偏差目標值為273.24TEU.

從求解結果可以看出，運用本文建立模型來均衡堆場的箱區資源，優化效果顯著.該模型不僅平衡了船舶在各箱區中的作業量，提高了堆場對船舶作業的服務效率，降低了船舶的在港時間，而且平衡了整個堆場箱區間的作業量，提高了裝卸設備的作業效率，進而實現了集裝箱箱區內空間資源的優化.

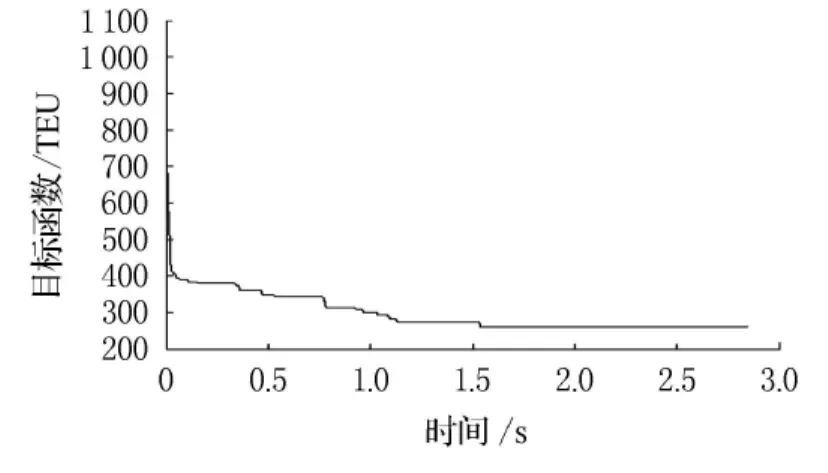
圖2 標函數收斂圖

4 結束語

在滾動計劃的基礎上，以提高堆場空間資源的利用率和裝卸設備資源的作業效率為目標，建立了基于混堆模式的箱區間作業量均衡優化模型，并采用模擬退火算法進行求解.通過實際的案例分析，驗證了模型及算法的有效性，結果顯示該模型能夠提高堆場空間資源的利用率.隨著研究內容的深入，仍需進一步考慮如何確定每艘船舶分配到各個箱區貝位中的裝卸箱量，從而縮短船舶在港時間，提高集裝箱碼頭的服務效率.

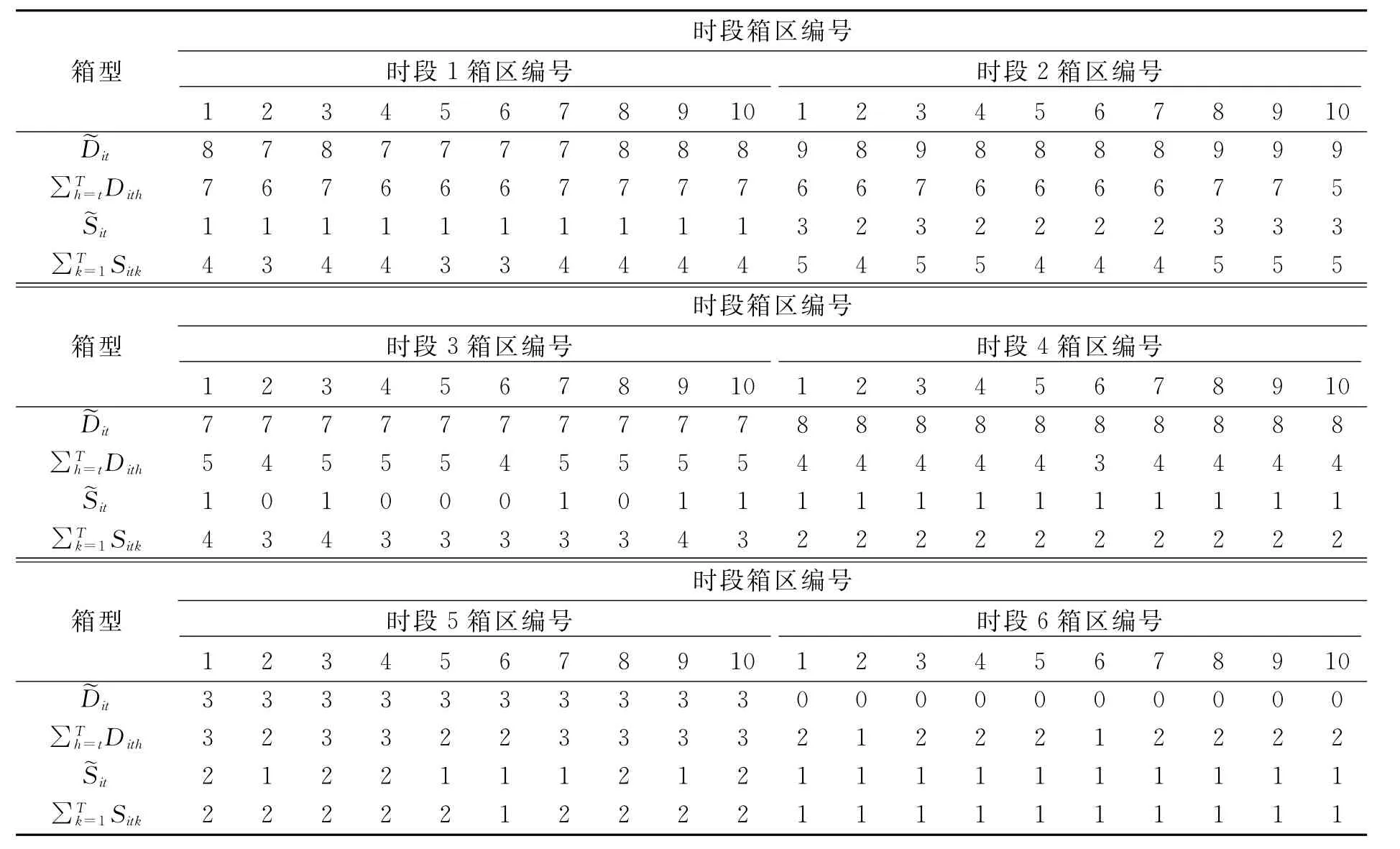
表4 各箱型在各時段分配到各箱區的箱量

［1］PRESTON P，KOZAN E.An approach to determine storage location of containers at seaport terminals［J］.Computers ＆ Operations Research，2001，28：983－995.

［2］CHEN P，FU Zhaohui，LIM A.The yard allocation problem［C］.Eighteenth National Conference on Artificial Intelligence，2002：56－65.

［3］ZHANG Chuqian，LIU Jiyin，WAN Yatwah.Storage space allocation in container terminals［J］.Transportation Research Part B，2003，37：883－903.

［4］徐德磊，韓曉龍，梁成姬.基于堆存能力的集卡優化分派研究［J］.武漢理工大學學報：交通科學與工程版，2011，35（9）：77－81.

［5］王 斌.集裝箱堆場基于混堆的滾動式計劃堆存方法［J］.系統工程學報，2005，20（5）：466－471.

［6］王 斌.集裝箱碼頭堆場的一種動態隨機堆存方法［J］.系統工程理論與實踐，2007，27（4）：147－153.

［7］陶經輝，汪 敏.基于混堆模式的集裝箱堆場區段分配［J］.系統工程理論與實踐，2009，29（8）：185－192.

［8］徐 亞，陳秋雙，龍 磊，等.基于多目標規劃的堆場空間分配問題研究［J］.系統工程學報，2009，24（3）：365－369.