基于實測數據的路段可靠性近似算法研究＊

高愛霞 陳艷艷

（北京警察學院治安系1） 北京 102202） （北京工業大學交通工程北京市重點實驗室2） 北京 100022）

在路網中沒有異常事件發生的情況下，交通系統的隨機性主要由交通流量［1－3］的變化導致的，因此常態下，對于確定的路網而言，其可靠性主要是由交通流量及其變化決定.本文利用實測數據分析交通流量的變化規律，研究在流量波動范圍固定的情況下，飽和度與可靠度之間的關系，從而簡化可靠度的計算，使該指標更方便的應用于交通管理和規劃.

1 交通流量的變化規律分析

為了分析典型時段的流量分布特征，選擇高峰時段為分析對象.分析所用數據是北京市2011年4月～6月期間利用視頻檢測設備采集得到的快速路和主干路流量數據，共計90d.首先對2011年4月～6月不同月份工作日的早高峰時段路段流量的概率分布進行擬合.其中，工作日選取周一至周五的數據，早高峰時段設為07：00～09：00，選擇每個工作日的最大15min高峰交通量換算為相應的高峰小時流率，然后進行采集時間內的同一高峰時段的流量分布檢驗，交通流量概率分布擬合和檢驗的基本步驟如下.

步驟1 進行數據預處理，研究常態下的交通流量的變化規律，須剔出異常情況下的流量數據，需對數據進行質量控制.

步驟2 選擇路段流量作為數據樣本，對該數據樣本做頻數分析，勾畫流量的直方圖，對流量的概率分布征進行初步分析.

步驟3 進行正態分布的Kolmogorov－Smimov檢驗（K－S檢驗）［4］.K－S檢驗可以檢驗樣本數據是否服從指定的正態分布.K－S檢驗的結果用統計量D對應顯著性水平來判斷.若相伴概率p值大于指定的顯著性水平（通常取0.05），則接受本數據服從正態分布的零假設；如果小于指定的顯著性水平，則拒絕假設.

對快速路、主干路早高峰時段的流量數據概率分布進行曲線擬合，結果見圖1～6.

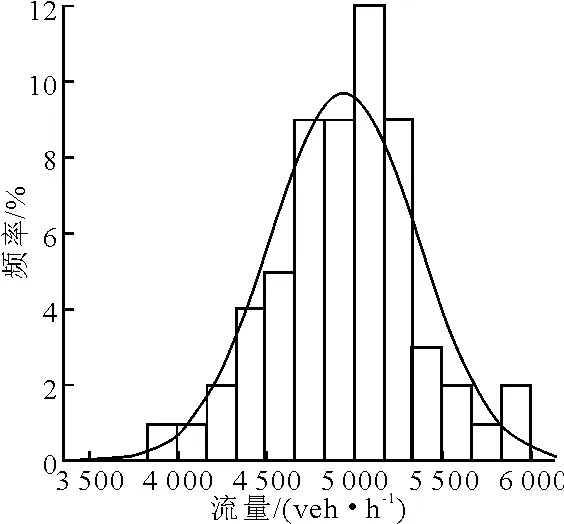
圖1 西直門－積水潭

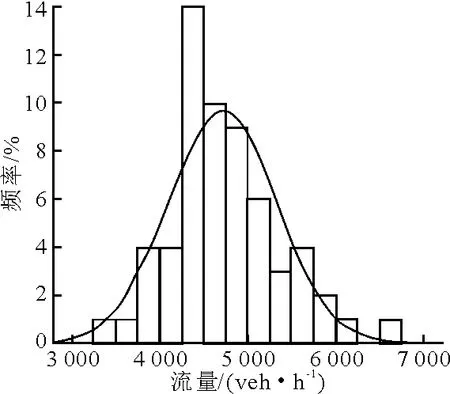
圖2 積水潭－西直門

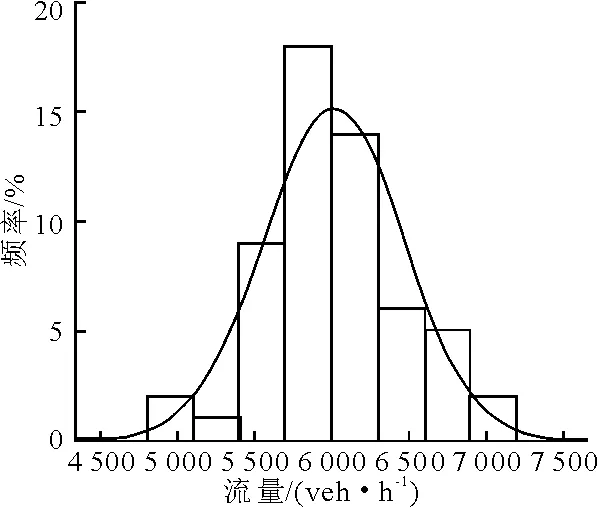
圖3 聯想橋－四通橋

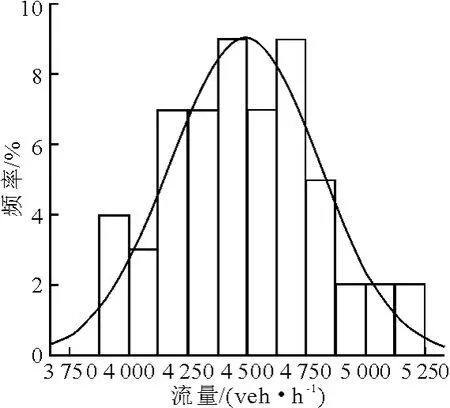
圖4 四通橋－聯想橋

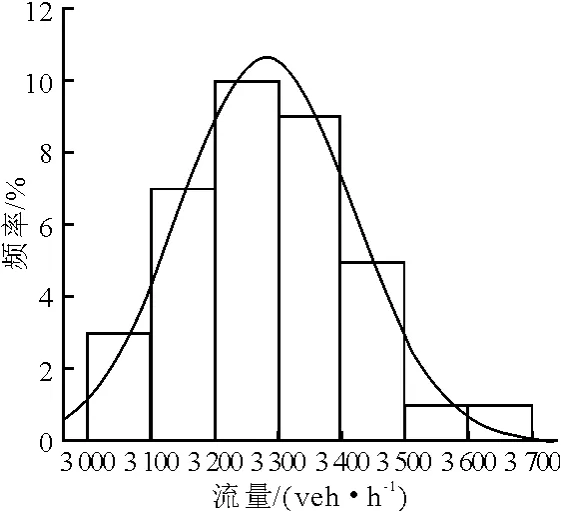
圖5 地鐵路

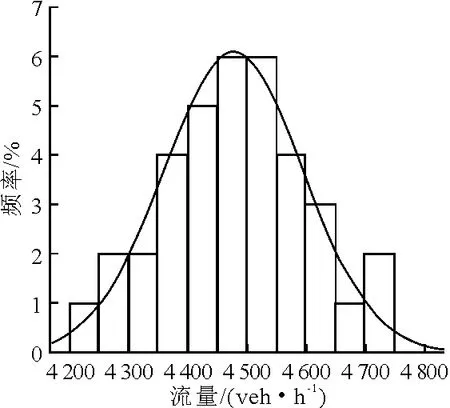
圖6 平安大街

K－S檢驗結果見表1.

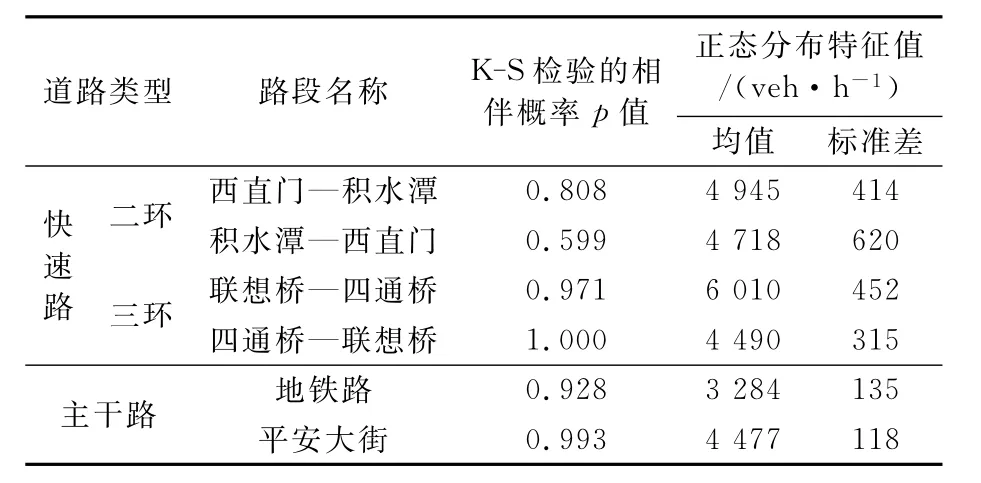
表1 不同等級路段高峰小時流量正態分布檢驗結果及特征值

由表1可見，6條路段的p值均大于0.05，則6條路段均通過“交通流量服從正態分布”的K－S檢驗.因此，可以假設快速路和主干路交通流量的概率分布為正態分布.

2 速度－流量關系分析

本文利用速度參數計算可靠度，為了確定可靠度與飽和度之間的關系模型，首先尋找速度－流量關系.根據統計數據，繪制速度－流量散點圖，見圖7.

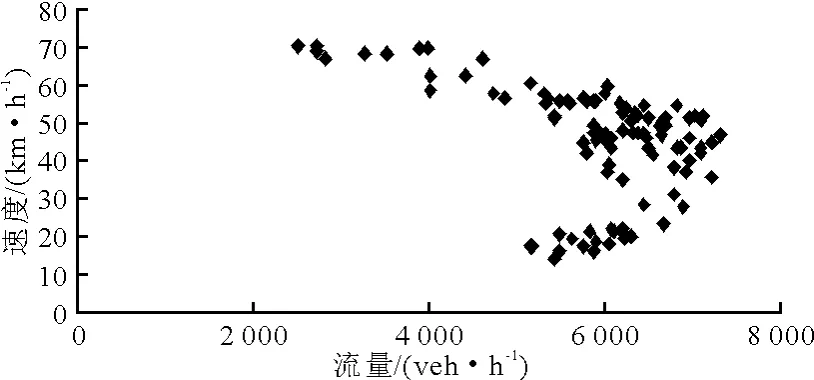
圖7 快速路流量－速度散點圖

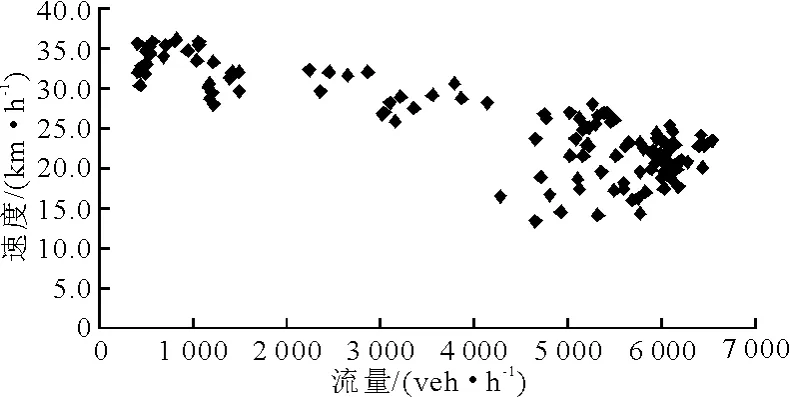
圖8 主干路流量－速度散點圖

從實測數據的速度－流量散點圖7、圖8可以看出：速度－流量散點的分布形式呈拋物線狀，這與 Greenshields所指出的速度－流量曲線［5－6］形狀基本相同，但是在阻塞流階段，當流量趨于零時，速度值并不是趨于零.用spss統計分析軟件擬合速度－流量關系曲線，通過數據擬合得出了快速路與主干道速度－流量曲線模型的參數值范圍、檢驗判定系數和曲線模型形式見表2.模型的檢驗判定系數R2達到了0.85以上，這說明曲線的擬合效果是比較好的.

表2 速度－流量關系曲線擬合模型

3 飽和度及流量波動與可靠性的關系研究

根據交通流量的正態分布特性以及流量－速度的關系模型，可以計算在交通流量波動范圍（流量標準差與其均值的比值）一定的情況下，每一個平均飽和度值所對應的速度參數，利用此速度參數根據暢通可靠度的計算方法［7］計算對應的可靠度值，從而可以得到平均飽和度與可靠度之間的一一對應值.圖9～圖11為計算得出的不同流量波動范圍內，飽和度與可靠度的對應值.其中可靠度為路網處于基本暢通常態的可靠度［8］，相當于單位距離出行時間閾值為2.0min／km.

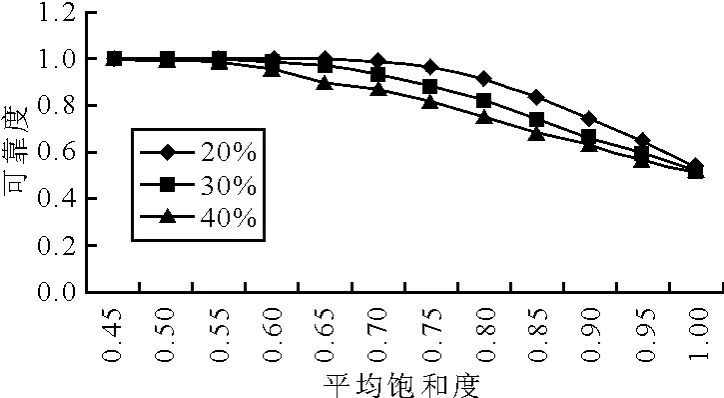
圖9 快速路的飽和度（欠飽和）及流量波動與其可靠度的對應值

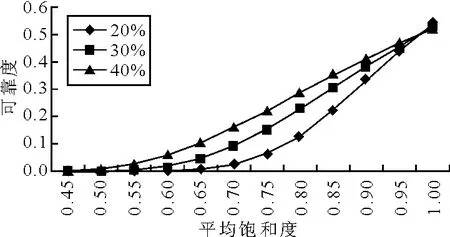
圖10 快速路的飽和度（超飽和）及流量波動與其可靠度的對應值

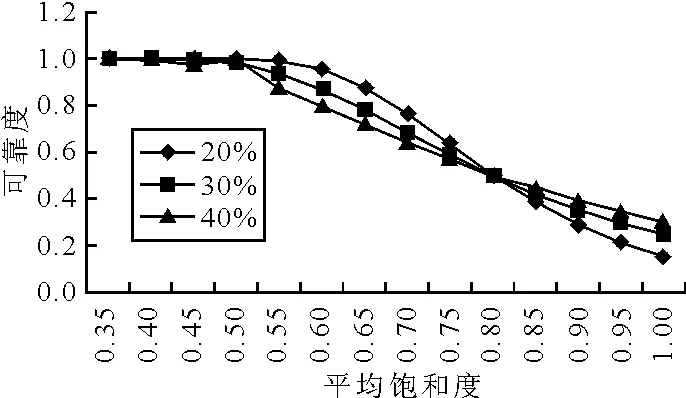
圖11 主干路的飽和度（欠飽和）及流量波動與可靠度的對應值

由圖9可以見，不同的流量波動，對于同一飽和度，對應的可靠度不同.波動范圍越大，可靠性越差.同時在欠飽和的情況下，隨著飽和度的升高，可靠度下降，當飽和度趨近于1時，可靠度下降至0.5左右，表明路網處于臨近飽和的狀態下，可靠性大大降低，有近50%的車輛速度達不到標準暢通速度.由圖10可見，當超飽和度達到0.5以下，可靠度接近0，即此刻狀態下所有車輛的速度都達不到標準暢通速度.由圖11可見，當飽和度接近于1時，可靠度下降至0.2左右，接近80%的車輛車速達不到標準暢通狀態.利用spss軟件進行曲線回歸，得到快速路和主干路的飽和度與可靠度的關系見表3.

表3 快速路、主干路飽和度（S）與可靠度（R）的函數關系

4 模型的驗證

根據得到的飽和度與可靠度的函數關系，可以求得快速路與主干路其他路段的可靠性，然后與利用統計法［9］得到的可靠度值（參考值）比較，驗證該算法在其他路段的適應性.利用該算法與統計法分別得到的可靠度值見表4.

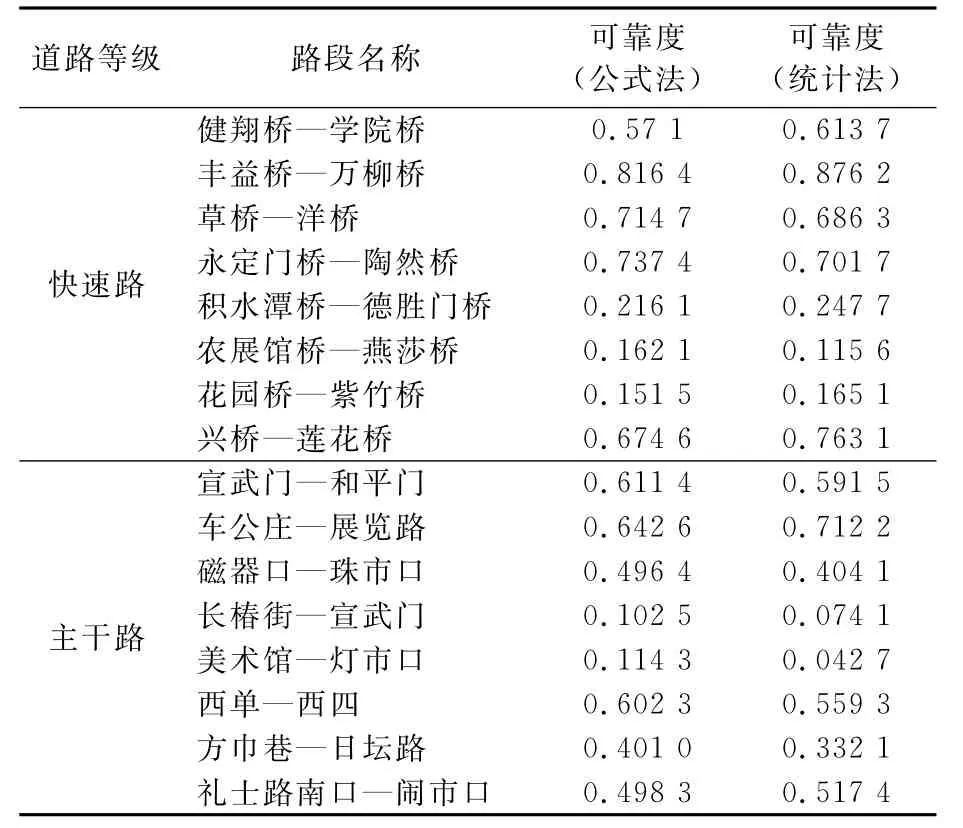
表4 可靠度的計算值與參考值比較

由表4可見，快速路中利用公式法與利用統計法得到的可靠度最大相差0.088 5；在主干路中用不同方法計算得到的可靠度值最大相差0.092 3.這是由于流量－速度模型的標定及飽和度與可靠度的函數關系擬合過程中都有不同程度的近似，導致最終的計算值與實際值會有不同程度的差別.但是最大誤差沒有超過10% ，因此在可靠度計算中可以采用該方法.

5 結束語

本文提出的算法與以往的算法相比，計算較為簡單，已知飽和度和流量波動范圍，就可以很容易的獲得路段的可靠度值.此方法運用于路網的規劃、設計與管理中，可有效地對規劃設計方案及管理措施進行可靠性評價，為設計及管理部門決策提供支持.

［1］IIDA Y.Basic concept and future directions of road network reliability analysis［J］.Journal of Advanced Trnsportation，1999，33（2）：125－134.

［2］ASAKURA Y，KASHIWADANI M.Road network reliability caused by daily fluctuation of traffic flow［C］∥19thPTRC Summer Annual Meeting，Proceedings Seminar G，1991：73－84.

［3］高愛霞，陳艷艷.異常事件下路網恢復可靠性研究［J］.武漢理工大學學報：交通科學與工程版，2010，33（2）：517－520.

［4］阮桂海，蔡建平，劉愛玉.數據統計與分析：spss應用教程［M］.北京：北京大學出版社，2005.

［5］高愛霞.城市路網可靠性及其保障技術研究［D］.北京：北京工業大學，2010.

［6］任福田.新編交通工程學導論［M］.北京：中國建筑工業出版社，2011.

［7］陳艷艷，劉小明，梁 穎.可靠度在交通系統規劃與管理中的應用［M］.北京：人民交通出版社，2006.

［8］梁 穎.城市交通系統暢通可靠性分析與優化［D］.北京：北京工業大學，2005.

［9］唐茜茹，陳艷艷，段衛靜.城市路網暢通可靠度計算方法及其應用［J］.城市交通，2011（1）：40－46.