基于熵風險度量的混合期望效用模型研究＊

文 秘 李偉兵

（1.陸軍軍官學院研究生管理大隊一隊 合肥 230031)（2.陸軍軍官學院研究生管理大隊二隊 合肥 230031)

1 引言

對于風險決策問題，期望效用理論普遍被認為是一個“有理性”選擇的規(guī)范化模型，并且廣泛的應用于各種經濟行為的描述性模型中，它假定人們在面對風險決策問題時，總是選擇期望效用最大的行動或方案。但是，Allais悖論［1］及Kahneman和 Tversky展望理論［2］中共同后果效應（Common consequence effect)和 共 同 比 率 效 應 （Common ratio effect)的提出，說明在實際做決策或者選擇時，許多人都不遵守最大期望效用理論，且該理論僅僅包含決策偏好的描述，缺乏對決策風險的度量。與此同時，主觀期望效用理論無法對Ellsberg悖論［3］中人們對不確定性規(guī)避現象做出解釋，主觀概率作為人們在有不確定性時決策的根本依據的假設受到了質疑。因此，用一個合適的尺度對不確定性進行度量，并將其納入到決策的過程，成為了當前風險決策問題研究的重要方向。本文在前人期望效用理論研究的基礎上，提出了一個基于熵風險度量的混合決策準則，建立了與之相關的風險決策模型，并成功地解釋了“共同比率效應”。

2 基于熵的風險度量

經典規(guī)范化的風險決策模型由三部分組成：狀態(tài)空間Θ＝｛θ｝，行動空間A＝｛α｝和定義在A×Θ上的支付函數X＝X（α，θ)，記為G＝（Θ，A，X)。假定決策者的效用函數為u（X)，有時記為u（X（α，θ))或u（α，θ)，這樣一個一般的決策模型寫成G＝（Θ，A，u)。對于一般的決策模型G＝（Θ，A，u)，α∈A，采取行動α對應的狀態(tài)θ有先驗分布πα（θ)。下面給出決策行動對應狀態(tài)的熵的風險度量定義。

定義1 給定的風險決策問題G＝（Θ，A，u)，行動方案α∈A，則a行動對應狀態(tài)的熵的風險度量為

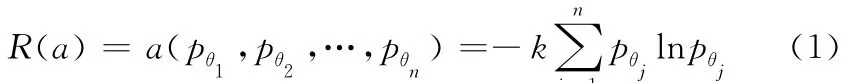
在信息學中，熵R（a)是不確定性的指標［4］，它認為一個廣泛的分布比具有明顯峰值的分布更加不確定，這與在Ellsberg悖論中的決策者不確定規(guī)避，即相對于較確定的事物，人們不喜歡更不確定或更含糊的事物現象相符合。因此，用熵去度量不確定性風險的程度是科學的、合理的。

3 混合決策準則

對于一個一般的風險決策模型G＝（Θ，A，u)，它必然包含一部分的確定成分與一部分的嚴格不確定成分，我們可以將其看成是一個狀態(tài)概率分布估計可靠的決策模型與對真實的自然狀態(tài)一無所知的（嚴格不確定)的決策模型的加權組合。基于這個觀點提出了如下的風險決策準則：

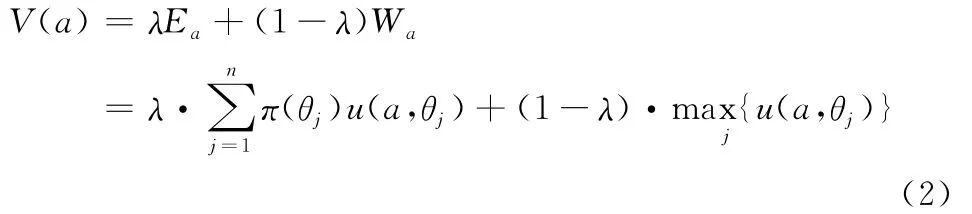
其中，λ（0≤λ≤1)是估計的該風險決策問題的狀態(tài)概率分布的可靠系數，Ea表示Bernoulli決策準則（又稱期望效用極大化準則或期望損失極小化)，Wa表示Wald悲觀決策準則。V（a)越小，則行動方案a越優(yōu)。當λ＝1時，表示狀態(tài)概率分布估計完全可靠，則：

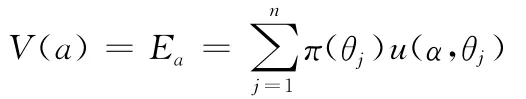
則該準則退化為Bernoulli決策準則Ea；當λ＝0時，表示狀態(tài)概率分布估計完全不可靠。則：

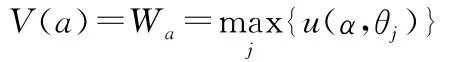
該準則退化為求解嚴格不確定型問題的Wald悲觀決策準則。該準則實際上是Bernoulli準則（Ea)與求解嚴格不確定型問題的Wald悲觀決策準則（Wa)的線性組合。

4 基于熵風險度量的混合決策模型

在上面的混合決策準則式（2)中，λ（0≤λ≤1)是所估計的該風險決策問題狀態(tài)概率分布的可靠系數，而我們定義的熵是R（a)刻畫不確定性的指標，因此若令λ＝1－R（a)，則該決策準則變?yōu)?/p>

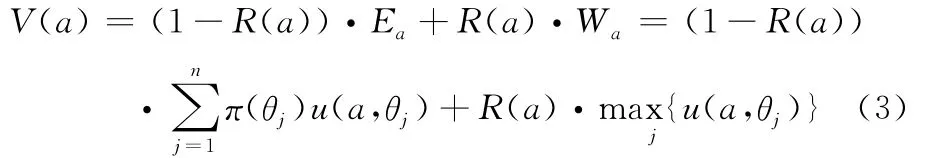
其中，取R（a)中的k∈（0，1/ln（n))為風險折扣系數，k值的上界是由λ≥0決定的，這就是基于熵風險度量的混合決策準則。下面定義在基于熵風險度量的混合決策準則下的風險決策模型。

定義2對于風險決策問題G＝（Θ，A，u)，設a1，a2∈A，記V（a1)，V（a2)分別為行動方案a1和a2在基于熵風險度量的混合決策準則下的得分值，簡稱熵－混合值。如果V（a1)＜V（a2)，則稱在基于熵風險度量的混合決策準則下，行動方案a1優(yōu)于行動方案a2，記為a1?a2；即有：

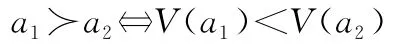
如果V（a1)≤V（a2)，則稱在基于熵風險度量的混合決策準則下，行動方案a1不劣于行動方案a2，記為a1≥a2，即有：

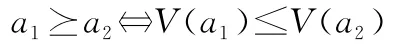
如果兩個行動方案a1和a2有相同的熵－混合值，此時有V（a1)＝V（a2)，則認為這兩個行動方案是無差異的，記為a1～a2；即有：

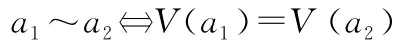
如果存在行動方案a＊∈A，使得則稱行動方案a＊為在基于熵風險度量的混合決策準則下的最優(yōu)方案。

稱這種決策模型為基于熵風險度量的混合決策模型。利用基于熵風險度量的混合決策方法可以將行動空間中的每一個行動方案按照其熵－混合值的大小進行排序；然后找一個行動方案，使得該方案的熵－混合值達到最小，此行動方案就是最優(yōu)方案。由定義2可知，基于熵風險度量的混合決策模型將決策行動的風險和決策者的偏好結合起來，使得決策行動的風險度量與決策者的偏好相容。下面給出基于熵風險度量的混合決策模型的性質。

性質1對于風險決策問題G＝（Θ，A，u)，若對任意行動都能在一定程度上取得所有的狀態(tài)θ，則有：

1)若行動空間中的所有行動方案的期望效用（損失)值都相同，則熵風險最小的行動方案即為最優(yōu)行動。

2)若行動空間中的所有行動方案對應的狀態(tài)的熵都相等，則期望損失值最小的行動方案為最優(yōu)行動。

顯然，該性質只是給出了在對任意行動a都能在一定程度上取得所有狀態(tài)θ這種特殊情況時的決策規(guī)律。對于任意情形下，a并不能在一定程度上取得所有狀態(tài)θ，此時決策準則中的參數k會隨實際能取得的狀態(tài)的個數而改變，Wa部分不再是定值。因此，在一般情形下V（a)會受到Ea、R（a)及Wa的共同影響，需要具體問題具體分析，計算出各個方案下的V（a)值進行決策。以共同比率效應［5］為例，證明基于熵風險度量的混合決策模型解釋實際問題的能力。有如圖1所示的兩個選擇問題：

圖1 共同比率效應決策行動

實驗表明絕大多數人，對于問題一，在a1和a2中選擇a1，而對于問題二，在a3和a4中選擇a4。這也與期望效用理論的獨立性公理不相容。

如果決策者是風險中型的，即效用函數是線性的，假設為u（x)＝x，于是得到：

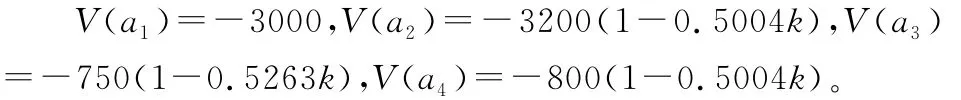
為符合實際大多數人的選擇，只需要滿足：

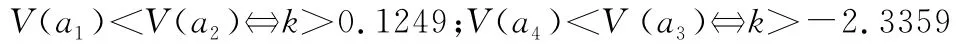
又∵k∈（0，1/ln（n))，其中n＝2

則0.1249＜k≤1.4427，即決策者的風險折扣系數在（0.1249，1.4427)內就可以預測決策者所采用的行動方案。

在一般情況下，決策者可以根據已獲得的歷史資料數據以及主觀知識（包括經驗、知覺和判斷等)，對未來自然狀態(tài)發(fā)生的概率作出主觀估計（即先驗概率)。然而，它很難準確地反映客觀真實情況，特別是對于本文研究的戰(zhàn)場目標配置問題，信息的時效性極強，當得到新的情報和信息，就必須立刻對自然狀態(tài)的概率估計進行修正，從而改善決策的質量。Bayes分析就提供了一種利用Bayes定理，將獲得的新信息用于修正自然狀態(tài)的先驗分布，從而得到更接近實際狀態(tài)、更加準確的后驗概率分布，提高風險決策精度的科學方法。因此，要利用式（3)中的混合決策準則進行決策，且要加入信息修正的內容，令Ea＝r（π，δ)，即用Bayes風險函數代替期望損失函數，則得到信息修正下的熵風險度量的混合決策模型：

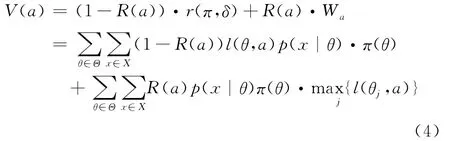
其中，l（θ，a)＝l（θ，δ（x))表示損失函數［6］。顯然式（3)只是式（4)在只有先驗信息下的特殊情況。這樣在決策準則方面進行過改進的基于熵風險度量的混合決策模型就能更好地應用于風險決策問題。

5 結語

改進的期望效用風險決策模型克服了傳統(tǒng)的期望效用模型不能將風險決策行動中的風險和決策者的偏好結合起來的問題，能使決策行動的風險度量與決策者的偏好相容。該決策模型很好地刻畫了決策過程中的主觀過程，從方法上降低了決策風險程度。

［1］Allais，M.，Le comportement de thomme rationnel devant le risqué：critique des postulats et axioms de I’Eclo Americaine［J］.Econometrica，1953，21：503546.

［2］D.Kahneman and Tversky A.，Prospect theory：an analysis of decision under risk［J］.Econometrica，1979，47：263291.

［3］Ellsberg D.Risk，ambiguity and the savage axioms［J］.Quarterly Journal of Economics，1961，75：643669.

［4］Shannon C.E.，A Mathematical Theory of Communication［J］.Bell System Technical Journal，1948，27：379423.

［5］Quiggin，J.，A theory of anticipated utility［J］.Journal of Economic Behavior and Organization，1982，3：323343.

［6］楊繼平.期望效用－熵決策模型與展望理論的解釋［J］.2008中國發(fā)展進程中的管理科學與工程，2008：16981701.

［7］李保明.效用理論與納什均衡選擇—對協(xié)調與合作問題的探討［M］.北京：經濟科學出版社，2003：99100.

［8］王愚，達慶利，陳偉達.基于模糊先驗概率的期望效用模型［J］.管理科學學報，2002，5（3)：3033.

［9］姜青舫.現代效用理論［M］.貴陽：貴州人民出版社，1990：204210.

［10］刁聯旺，梁維泰，于永生.具有正態(tài)隨機變量的多屬性決策統(tǒng)計方法［J］.計算機與數字工程，2012，40（10).

［11］徐玖平，吳巍.多屬性決策的理論與方法［M］.北京：清華大學出版社，2007：179180.