一種組合導航的直接法濾波算法

聞 新，紀 龍，趙建新

（南京航空航天大學 航天學院，南京 210016）

1 引言

組合導航系統以慣性導航系統 （inertial navigation system，INS）輔助全球定位系統 （global positioning system，GPS）接收機增強系統抗干擾能力，保證組合后的導航精度高于各系統單獨工作的精度［1-2］。組合系統直接法濾波的系統狀態方程為非線性方程［2］，這給濾波器設計帶來一定困難。針對該問題，部分學者在工作點處作線性化后采用擴展卡爾曼濾波 （extended Kalman filter，EKF）進行狀態估計，但當INS精度較低或載體處于高動態環境時，EKF算法參數估計精度不高甚至會發生濾波發散；另有學者在假設系統噪聲為白噪聲前提下，采用無跡卡爾曼濾波 （unscented Kalman particle filter，UPF）直接對非線性系統方程進行濾波估計，但這一方法僅在系統噪聲為白噪聲時成立。

粒子濾波 （particle filter，PF）在處理非線性、非高斯系統的參數估計問題上具有獨特優勢，對組合導航這類復雜問題的求解可獲得較高精度［3-5］。本文提出了基于 UPF的INS/GPS組合導航系統直接法濾波狀態估計，以INS的導航參數及平臺誤差角作為系統狀態，慣導力學編排方程和姿態誤差方程作為狀態方程，GPS的輸出作為觀測值，采用UPF直接進行組合導航系統參數解算。基于這一方案的系統狀態方程包含9個參數，減少了陀螺儀及加速度計漂移等狀態變量，降低了狀態變量維數易于粒子濾波實現。

2 INS/GPS組合導航系統濾波結構

本文INS/GPS組合導航系統基于閉環組合方式采用直接法濾波，INS和GPS分別對載體運動參數進行測量，將INS和GPS測得的參數分別送入UKF濾波器進行集中解算，從而獲得系統狀態的最優估計并作為組合導航系統的輸出，濾波輸出對INS系統進行狀態反饋修正。這種組合系統還能夠實現GPS信號無效時的容錯性，其結構如圖1所示。

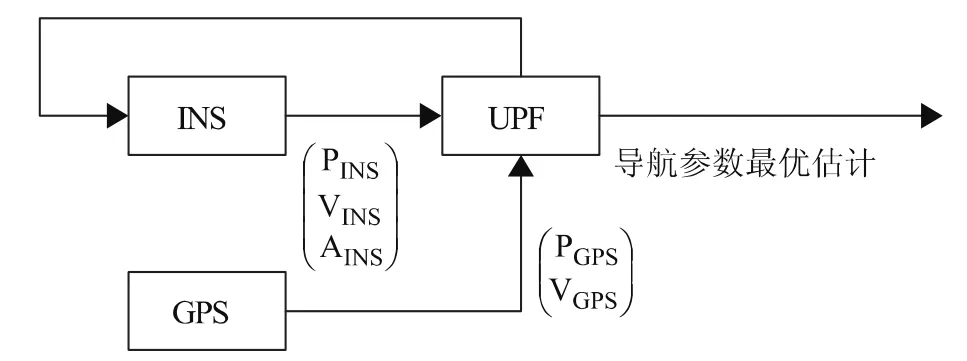
圖1 INS/GPS組合導航系統的直接法UPF濾波結構圖

3 基于UPF的INS/GPS組合導航系統直接法濾波算法

導航坐標系選為東北天地理坐標系，則慣導系統的力學編排方程和姿態誤差方程如式 （1）和式 （2）所示。

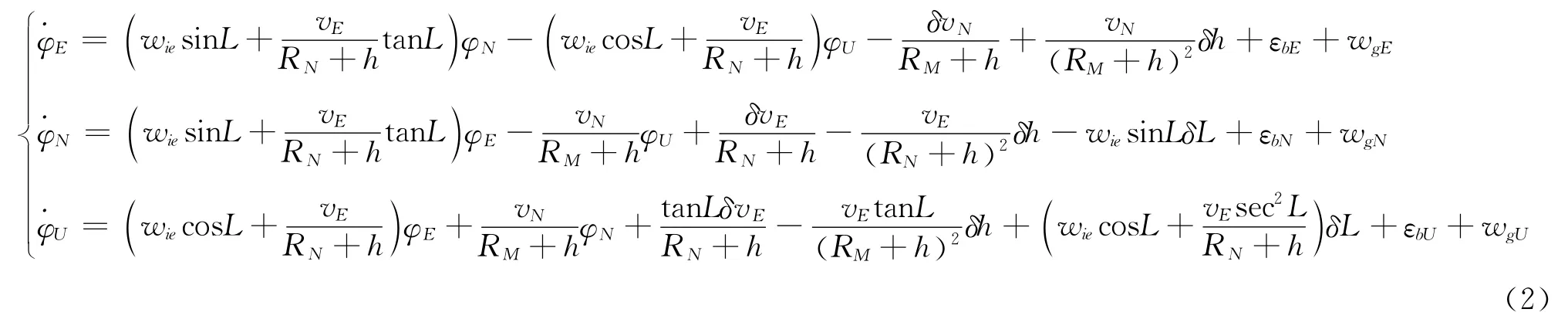
式中，vE、vN、vU為東、北、天向速度，L、λ、h為經度、緯度和高度，φE、φN和φU為東、北、天向姿態誤差角，系統以這9個參數作為狀態值。其中，fE、fU、fN為加速度計輸出的東北天向比力觀測值，δvE、δvN、δh和δL在實際計算中可以由INS和GPS的輸出差值近似獲得，εbE、εbN和εbU為陀螺的東、北、天向常值漂移。

3.1 系統狀態方程

為簡化系統模型并提高濾波計算效率，本文僅對東、北、天向位置、速度和姿態誤差建模，不對加速度計和陀螺進行誤差建模，則INS/GPS組合導航系統狀態向量為

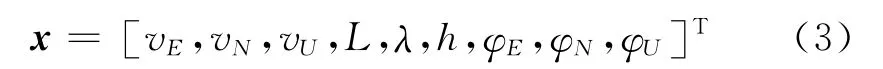
根據選取的系統狀態向量x，結合式 （1）、式（2）和式 （3），可列寫出INS/GPS組合導航系統的狀態方程為

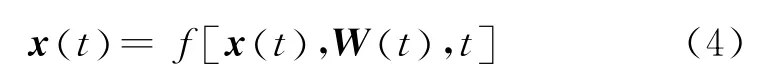
式 中，f［·］為 非 線 性 連 續 函 數，W（t）＝［wgE，wgN，wgU］T為系統噪聲。

3.2 觀測方程

以GPS輸出的速度信息vEGPS、vNGPS、vUGPS和位置信息LGPS、λGPS、hGPS為觀測值Z，即

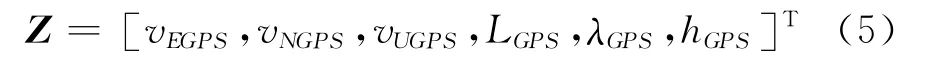
據前面所選取的系統狀態x和觀測值Z，可獲得組合導航系統的觀測方程

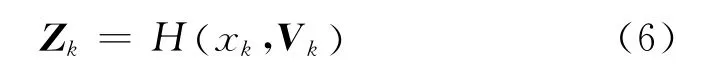
式中，Zk和xk為Z和x在k時刻的值，H（·）為線性函數，Vk＝ ［VVE，VVN，VVU，VL，Vλ，Vh］T為觀測噪聲，強度為Rk。

3.3 UPF濾波算法解算過程

基于個人計算機的解算過程要采用離散的系統方程，而INS/GPS組合導航系統狀態方程為微分方程。因此，需要對式 （4）進行離散化。離散化后的系統狀態方程

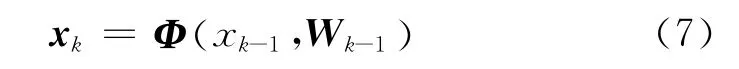
式中，F（·）為非線性離散函數，Wk為系統噪聲，噪聲方差強度為Qk。其中

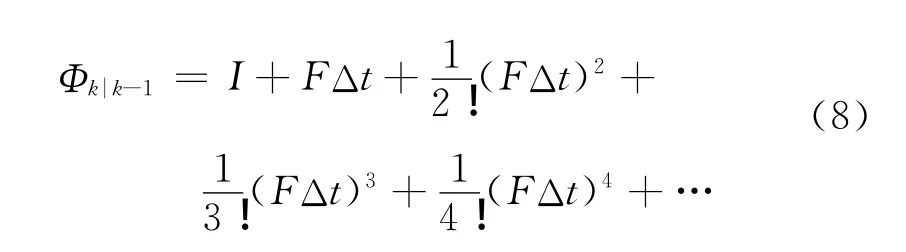
為減小系統離散化誤差，仿真過程中取前三項以減小離散化誤差。并且有

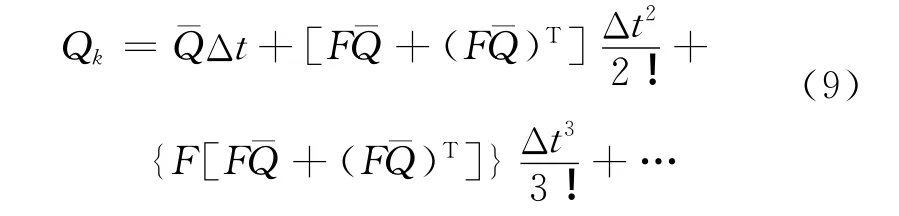
式中，Δt為濾波更新周期，＝Q。狀態方程和觀測噪聲如下

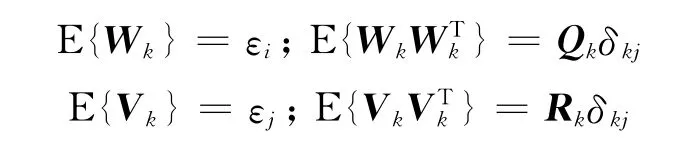
利用上面推導出的INS/GPS組合導航系統離散方程，結合UKF濾波法的遞推更新過程，得出基于UPF算法的組合導航系統濾波過程如下

1）初始化：k＝0

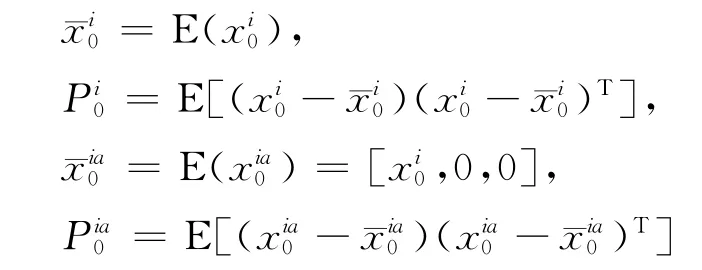
其中，＝x（t）t＝k。

2）重要性密度函數，k＝1，2，…，T，使用UKF更新粒子

其中na＝nx＋nw＋nv為擴展后系統狀態的維數，且，通過該式對狀態向量進行擴展。

（2）對每個采樣點，i＝1，2，…，N，應用UKF算法得到，，從而得到簡易分布函數

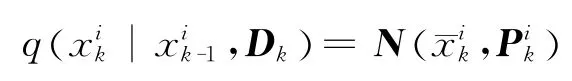
（3）從建議分布中抽取粒子：

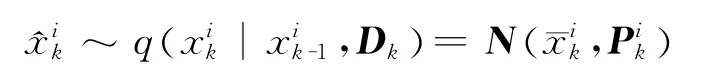
（4）計算粒子權值并歸一化

3）重采樣

對 ｛，｝ ，i＝1，2，…，N重采樣，得到新的粒子集合 ｛，｝ ，權值＝1/N，i＝1，2，…，N。

4）結果輸出

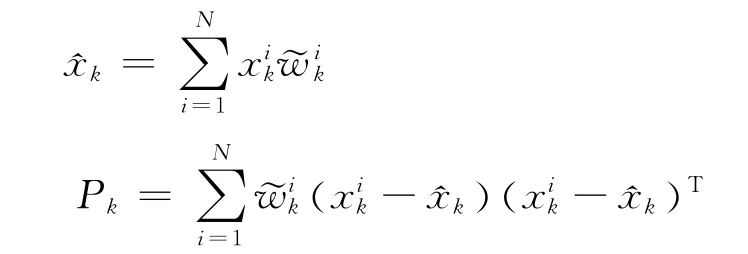
根據組合導航系統的離散狀態方程式 （7）和觀測方程式 （6），只須設定濾波初值，就可獲得第k時刻的系統狀態最優估計值xk，k＝1，2，3…。

4 仿真分析

本文主要研究INS/GPS組合導航數據融合算法的精度，仿真期間保證系統在組合模式下工作。INS/GPS組合導航系統的初始參數和仿真參數如表1和表2所示。仿真選取典型的飛機機動軌跡，該軌跡包含滑跑、加速拉起、爬高、改平、平飛、預轉彎、轉彎、減速飛行、低頭、俯沖等機動動作，仿真時長為3 600s，其軌跡如圖2所示。

表1 INS/GPS組合導航系統初始參數設置

表2 INS/GPS組合導航系統仿真參數設置

圖2 飛行軌跡仿真

在上述條件下，分別對INS/GPS組合導航系統的直接法UPF和UKF進行了仿真研究，并對仿真結果進行比較分析。為保證組合導航系統直接法濾波的精度并控制濾波計算量，濾波粒子數N取為1 000，并取α＝1，β＝0，k＝2。由于篇幅有限，且東向和北向導航結果具有相似性，本文僅對東向 （經度）、天向 （高度）的位置和速度誤差進行數值計算分析，其仿真結果如圖3、圖4所示。

從圖3和圖4可以看出，應用UKF組合導航系統經度誤差可控制在±13m以內，高度誤差在±15m以內，速度誤差在±0.6m/s以內。而應用UPF的組合導航系統經緯度誤差控制在±6m以內，高度誤差在±10m以內，速度誤差在±0.5 m/s以內。通過上述兩種濾波計算結果的比較，說明了基于UPF濾波的直接法INS/GPS組合導航系統可以獲得更高的導航精度，并能更準確地反映真實狀態的演變情況。

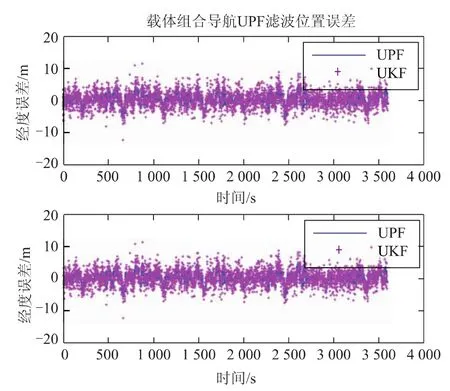
圖3 基于UPF和UKF算法的經度和高度位置誤差

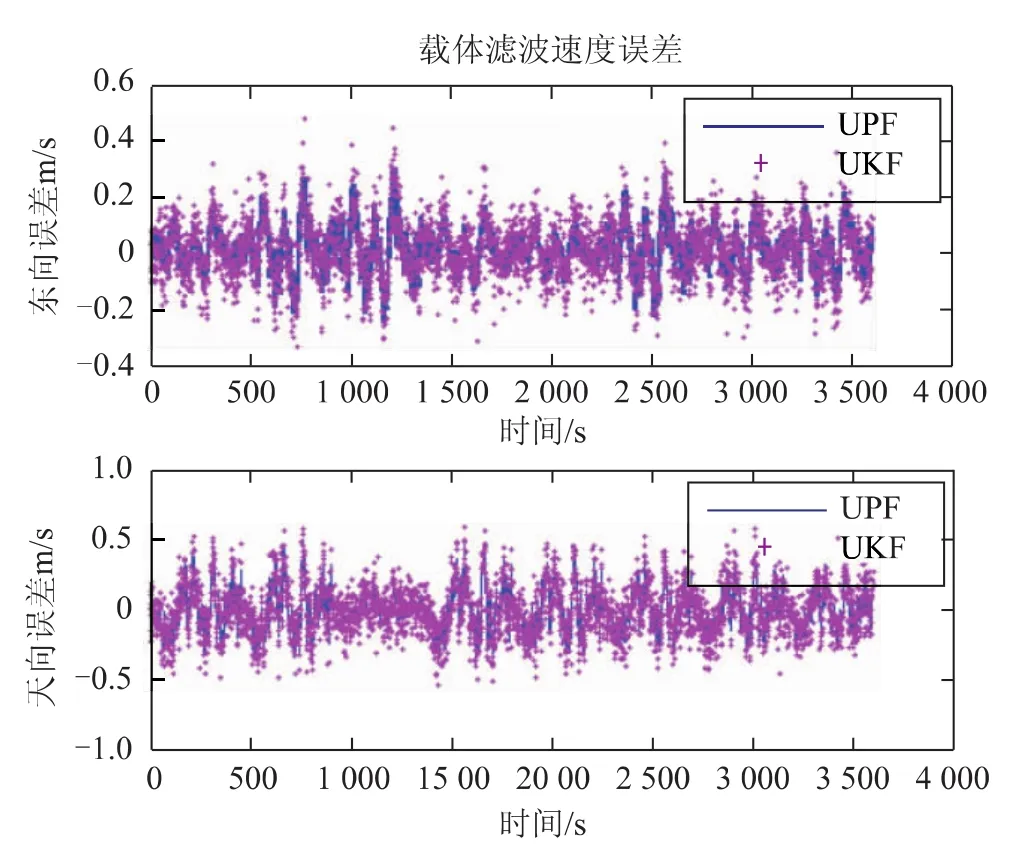
圖4 基于UPF和UKF算法的東向和天向速度誤差

5 結論

直接法UPF濾波在組合導航系統狀態結算過程中不含截斷誤差，濾波過程避免了慣導力學編排方程的許多重復計算，降低了算法冗余度。同時，閉環結構的濾波方法在GPS信號突然失效時系統可實現有效切換。仿真結果表明UPF算法與UKF算法相比，具有更高的估計效率和估計精度，解算過程具有較強的魯棒性。

［1］全偉，劉百奇，宮曉琳.慣性/天文/衛星組合導航技術［M］.北京：國防工業出版社，2011.

［2］劉建業，曾慶化，趙偉.導航系統理論與應用［M］.西安：西北工業大學出版社，2010.

［3］秦永元，張洪鉞，汪叔華.卡爾曼濾波與組合導航原理［M］.西安：西北工業大學出版社，1998.

［4］程水英，張劍云.粒子濾波評述［J］.宇航學報，2008，29（4）：1099－1112.

［5］趙琳，王小旭，丁繼成.組合導航系統非線性濾波算法綜述［J］.中國慣性技術學報，2009，17（1）：46－54.

［6］楊波，秦永元，柴艷.UKF在INS/GPS直接法卡爾曼濾波中的應用［J］.傳感技術學報，2007，20（4）：842－846.

［7］汪秋婷，胡修林.基于UKF的新型北斗/SINS組合系統直接法卡爾曼濾波［J］.系統工程與電子技術，2010，32（2）：376－379.

［8］BENGTSSON T，SNYDER C，NYCHKA D.Toward a Nonlinear Ensemble Filter for High Dimensional Systems［J］.Journal of Geophysical Research，2003，108（D24）：8775－8785.

［9］VAN DER MERWE R，DOUCET A，DE FREITAS N，etal.The Unscented Particle Filter［EB/OL］.［2013－02－16］.http：//automatica.dei.unipd.it/tl＿files/utenti/lucaschenato/Classes/PSC10 ＿11/UPF ＿slides.pdf.

［10］VAN DER MERWE R，DOUCET A，DE FREITAS N，eta1.The Unscented Particle Filter Technical Report［R］.Cambridge：Department of Engineering，University of Cambridge，2000.