分類突破電磁感應中的“雙桿”問題

張 超

（順德區容山中學，廣東 佛山 528303）

高考電磁感應綜合問題常常涉及到有關圖像、電路、動力學、能量和動量等知識點.這類問題重在考察學生的物理綜合能力，同時對物理思維和素養也有著較高的要求.“雙桿”問題是高考電磁感應綜合應用中難度較大的一類題型，在高考中可以說是常考不衰，而這類問題又恰恰是學生的薄弱環節.基于多年教學實踐，以下對這類問題進行簡要的分析和總結，供大家參考.

1 除安培力外，不受其他外力的水平導軌問題

1.1 導軌間距相等

例1.如圖1所示，在磁感應強度大小為B、方向垂直向上的勻強磁場中，有一上、下兩層均與水平面平行的“U”型光滑金屬導軌，在導軌面上各放一根完全相同的質量為m的勻質金屬桿A1和A2，開始時兩根金屬桿位于同一豎起面內且桿與軌道垂直.設兩導軌面相距為H，導軌寬為L，導軌足夠長且電阻不計，金屬桿單位長度的電阻為r.現有一質量為m／2的不帶電小球以水平向右的速度v0撞擊桿A1的中點，撞擊后小球反彈落到下層面上的C點.C點與桿A2初始位置相距為s.求：（1）回路內感應電流的最大值；（2）整個運動過程中感應電流最多產生了多少熱量；（3）當桿A2與桿A1的速度比為1∶3時，A2受到的安培力大小.

解析：（1）小球和桿A1組成的系統，由動量守恒定律得

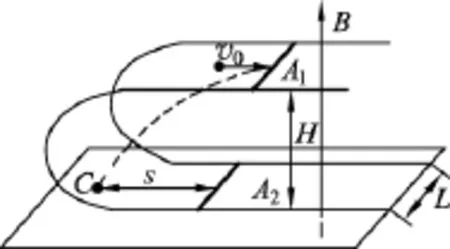
圖1

由（1）～（3）式解得

回路中感應電動勢的最大值

回路中感應電流的最大值

由（4）～（6）式解得

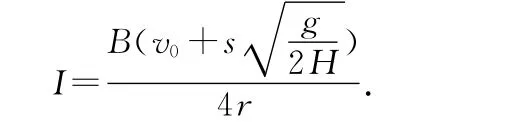
（2）對兩棒組成的系統，由動量守恒定律得

由能量守恒定律，整個運動過程中感應電流最多產生熱量為

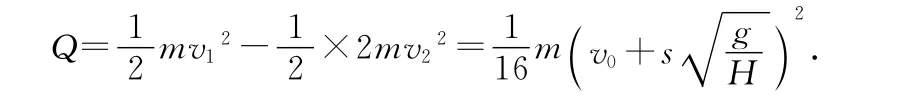
（3）由動量守恒定律得mv1＝mv1′＋mv2′，又

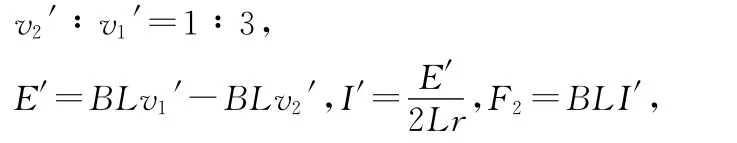
A2受到的安培力大小為

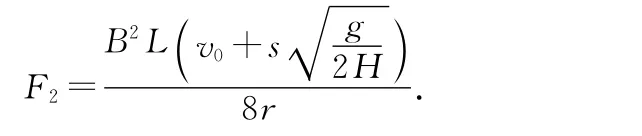
點評：本題是廣東高考題，具有典型代表意義.此類問題一般涉及動量守恒定律，能量守恒定律及電磁學、運動學相關知識，其最終狀態是兩桿以相同的速度做勻速運動.若兩桿運動方向同向則總電動勢為兩桿的電動勢相減，反向則相加.

1.2 導軌間距不等

例2.如圖2，足夠長的光滑平行導軌水平放置，電阻不計，MN 部分的寬度為2L，PQ部分的寬度為L，金屬棒a和b的質量ma＝2 mb＝2 m，其電阻大小Ra＝2Rb＝2R，a和b分別在MN和PQ上，垂直導軌相距足夠遠，整個裝置出于豎直向下的勻強磁場中，磁感應強度為B.開始a棒向右速度為v0，b棒靜止，兩棒運動時始終保持平行且a總在MN 上運動，b總在PQ上運動，求a、b最終的速度.

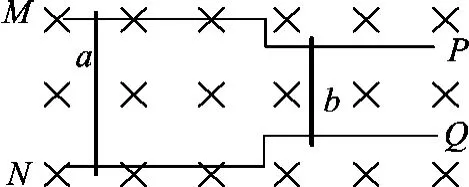
圖2

解析：由于兩棒切割長度不同，安培力大小不相等，故系統合外力不為0，系統金屬棒a和b動量不守恒，兩棒最終運動速度并不相等.金屬棒a和b運動方向相同，E總＝Ea－Eb＝2BLva－BLvb，通過動力學分析，兩棒加速度逐漸減小.當E總＝0，即2BLva＝BLvb時，兩棒加速度為0，將分別做勻速運動.則

分別對金屬棒a和b應用動量定理有

且

聯立（1）～（4）式求得

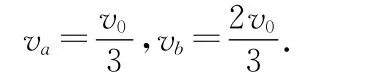
點評：對于導軌間距不相等的問題，往往不滿足動量守恒定律的條件的，因此其最后的速度也不會相同，兩導體棒最終以不同的速度做勻速運動，故不能定式思維入誤區.針對此類題目要使用動量定理、電磁學、動力學相關知識求解，也要注意電路總電動勢的計算方法.

2 除安培力外，單桿受其他恒定外力的水平導軌問題

例3.如圖3所示，兩根平行的金屬導軌，固定在同一水平面上，磁感應強度B＝0.5T的勻強磁場與導軌所在平面垂直，導軌的電阻很小，可忽略不計.導軌間的距離L＝0.2m，兩根質量均為m＝0.1 kg的平行金屬桿甲、乙可在導軌上無摩擦地滑動，滑動過程中與導軌保持垂直，每根金屬桿的電阻為R＝0.5Ω.在t＝0時刻，兩桿都處于靜止狀態.現有一與導軌平行，大小為0.20N的恒力F作用于金屬桿甲上，使金屬桿在導軌上滑動.經過t＝0.5s，金屬桿甲的加速度為a＝1.37m／s2，求此時兩金屬桿的速度各為多少？

解析：任一時刻t兩金屬桿甲、乙之間的距離為x，速度分別為v1和v2，經過很短時間Δt，桿甲移動距離v1Δt，桿乙移動距離v2Δt.回路面積改變為

由法拉第電磁感應定律，回路中的感應電動勢為

圖3

回路中的電流為

桿甲的運動方程為

由于作用于桿甲和桿乙的安培力總是大小相等、方向相反，所以兩桿的動量（t＝0時為0）等于外力F的沖量

由（1）～（5）式可求出

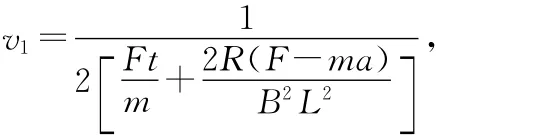
代入數據得v1＝8.15m／s，v2＝1.85m／s.

點評：這類問題應使用動量定理、電磁學和牛頓運動定律等相關知識進行分析.該題便是利用法拉第電磁感應定律、牛頓第二定律和動量定理聯立求解，這類問題如涉及到最終狀態，那么不難分析得出，兩導體棒最終會以不同的速度做加速度相同的勻加速運動.

3 豎直導軌問題

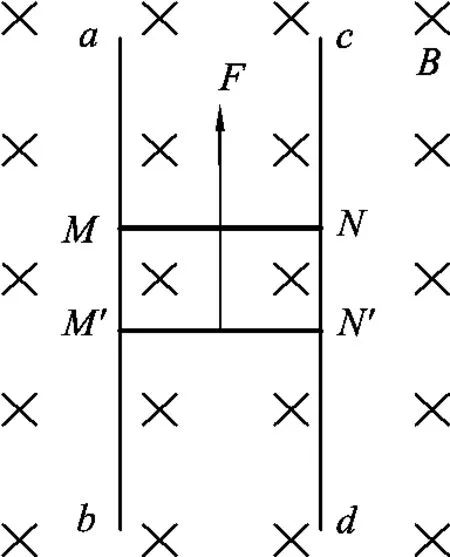
圖4

例4.（2011年海南高考題）如圖4所示，ab和cd是兩條豎直放置的長直光滑金屬導軌，MN和M′N′是兩根用細線連接的金屬桿，其質量分別為m和2 m.豎直向上的外力F作用在桿MN 上，使兩桿水平靜止，并剛好與導軌接觸；兩桿的總電阻為R，導軌間距為l.整個裝置處在磁感應強度為B的勻強磁場中，磁場方向與導軌所在平面垂直.導軌電阻可忽略，重力加速度為g.在t＝0時刻將細線燒斷，保持F不變，金屬桿和導軌始終接觸良好.求

（1）細線燒斷后，任意時刻兩桿運動的速度之比；

（2）兩桿分別達到的最大速度.

解析：設某時刻MN和M′N′速度分別為v1、v2.

（1）對于MN 和M′N′系統合外力為0，MN 和M′N′動量守恒，有mv1－2 mv2＝0，則

（2）當MN 和M′N′的加速度為0時，速度最大.M′N′受力平衡，有

根據閉合電路歐姆定律，有

電路的電動勢為

由（1）～（4）式得

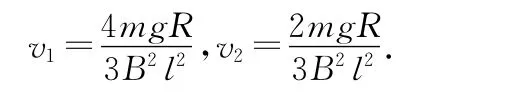
點評：作為2011年海南高考題，此題目是構思巧妙的豎直軌道“雙桿“問題.題目基于系統合外力為0，考察考生對系統動量守恒條件的理解和掌握，利用動力學分析雙桿的末狀態，同時還要特別注意，由于兩桿運動方向相反，故電路的總電動勢等于兩桿電動勢之和.

1 袁培耀.高考中的框架模型與“電磁感應”知識.物理教學探討，2006（10）.