利用互信息確定延遲時間的新算法

何鵬，周德云，黃吉傳，2

1.西北工業大學電子信息學院，西安 710129

2.中國人民解放軍駐成都飛機工業公司軍事代表室，成都 610092

利用互信息確定延遲時間的新算法

何鵬1，周德云1，黃吉傳1，2

1.西北工業大學電子信息學院，西安 710129

2.中國人民解放軍駐成都飛機工業公司軍事代表室，成都 610092

HE Peng,ZHOU Deyun,HUANG Jichuan.New algorithm for determining delay time by mutual information.Computer Engineering and Applications,2013,49（24）：8-10.

基于過程監控數據的故障診斷是保障復雜系統過程安全、避免重大事故的有效手段，復雜系統工作過程都可采集大量的數據，且這些信號通常表現為較強的非平穩性和非線性，使得對其進行故障特征的提取較為困難。傳統方法利用所有變量進行診斷，計算時間長且診斷精度低，增加了系統操作和維護的成本[1]。隨著非線性動力學研究的不斷進步，特別是將混沌時間序列信號的相空間重構理論[2]應用于設備故障診斷領域，可以從單變量的時間序列中獲取系統的有效性息，如相關維數[3]、Lyapunov指數[4]等動力學指標，揭示了故障的本質，從全新的角度更深刻地認識了復雜的非線性動力系統的行為[5]。另外人們將相空間重構理論廣泛地應用于各種工程領域，如傳感觀測信息融合壓縮方法及其故障診斷[6]、電力負荷預測[7]等，均獲得了讓人意想不到的卓越效果。

1 相空間重構

Takens[2]提出的相空間重構方法往往作為對非線性時間序列進行分析的第一步。其基本原理為：由于系統任何一個分量的演化都是由與之相互作用的其他分量所決定的，因此采用時間序列中某些固定的延遲時間的數據點作為重構相空間的高維來處理，即X(n)=[x(n),x(n+τ),x(n+2τ),…,x(n+(m-1)τ)]，重構出軌跡可以表征原混沌系統吸引子的動力學特征，與其微分拓撲結構一致。Takens[2]已經證明，對于一個無限長的無噪聲時間序列，延遲時間τ的選取是任意的。然而在實際運用中，采樣得到的時間序列必然是有限且含有噪聲的，此時恰當選取參數m與τ對重構質量有著至關重要的影響。

選擇τ的基本思想是使原采樣序列和其延遲序列具有某種程度的獨立又不完全無關，從而可以將相鄰數據點x(n)和x(n+τ)可以作為相空間重構中的獨立坐標來處理。τ太小會造成相鄰分量之間的信息冗余，計算量劇增；τ太大會使相鄰坐標完全獨立，無法獲取有效的信息來實現相空間重構。

目前確定重構最佳延遲時間τ的方法主要有三種：自相關函數法[8]、平均位移法[9]與互信息法[10]。其中自相關函數法主要選取序列自相關函數Rxx(τ)第一次降至0的值作為最佳延遲，該方法是對數據線性相關性的描述，本質上不適合分析非線性情形；平均位移法屬于一種幾何方法，取平均位移函數的斜率降至初值的40%的值作為最佳延遲，具有一定的隨意性，理論性不強，并且該方法的結果與嵌入維數m的選取有關，與其構成的聯合算法[11]需要反復實驗，直到結果收斂一致為止，較為繁瑣。采用序列互信息函數的第一局部極小值作為最佳延遲的方法，理論基礎完善，且可獨立于嵌入維數m進行單獨選取，較為理想。但在實際運用中由于互信息的計算量大，難以編程實現等特點極大地限制了它的運用。

2 計算序列間的互信息

從信息論[12]的角度出發，采用平均互信息量來計算采樣序列與其延遲序列的關聯程。在利用系統某一變量的觀測值作為時間序列來進行相空間重建的過程中，取得的觀測點列為x(i)，i=1,2,…,N′，為分析x(n)和x(n+τ)之間的相關性，選取延遲量x(i+τ)構成新的點列y(i)，通過計算x(i)和y(i)的互信息大小即可獲得其相關性，其中τ=n×t，t為采樣間隔時間，構成點對總數為N，N=N′-n。

由于隨機變量X或Y的發生及兩者間的相關性，使其不確定性減少的熵稱為互信息，計算表達式如下：

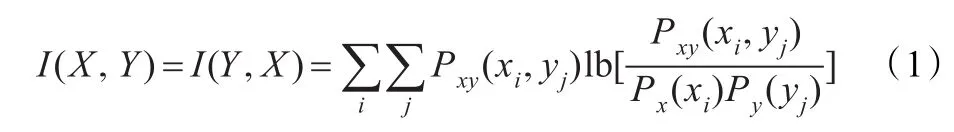
其中，P(xi)為事件xi單獨發生的概率，P(yj)為事件yj單獨發生的概率，P(xi,yj)為事件xi，yj同時發生的概率。

互信息的計算較為復雜，主要通過對X（橫軸），Y（縱軸）的不同劃分來進行分類，這里采用Fraser[10]提出的互信息算法，是在邊緣分布等概率的基礎上劃分網格，如圖1。

圖1 等概率劃分網格示意圖

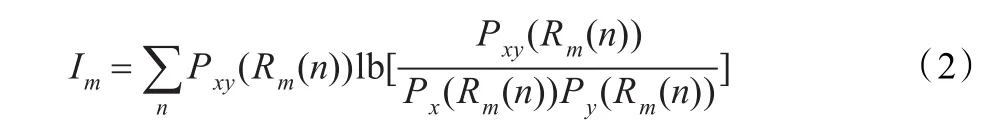
其中，n=1,2,…,Zm，分別對應該層劃分的某個網格(xi,yj)，Rm代表進行的是第m層劃分。

得到計算系統互信息的遞推公式，設

其中網格是否稀疏采用χ2分布的相應準則來判斷。根據χ2分布累積分布函數的對照表，χ2分布可以用來測試隨機變量之間是否相互獨立，也可用來檢測統計模型是否符合實際要求。本文可以根據已經設定的網格是否稀疏的閾值，然后對照分布函數的對照表，進一步判斷網格是否稀疏，文獻[13]中也采取了類似的判斷原則。

3 利用互信息確定延遲時間的改進算法

從整體上說，所有現實中的混沌運動系統都是耗散系統[14]，它們在相空間的軌線最終都要收縮到捕捉區中并形成吸引子，具有全局穩定性。但是就局部來說，吸引子內部的運動又是不穩定的，相鄰軌道之間相互排斥而按指數形式分離。混沌運動的吸引子是由軌線經過大量的分離和折疊才形成的，把吸引子局部無限放大，可以發現，其內部的結構與形狀具有無窮層次的自相似結構，即分形，其運動軌跡具有各態歷經性。正是由于混沌吸引子的這些特性，在計算該系統互信息時，往往會出現波峰與波谷交疊的情形，如圖2所示。

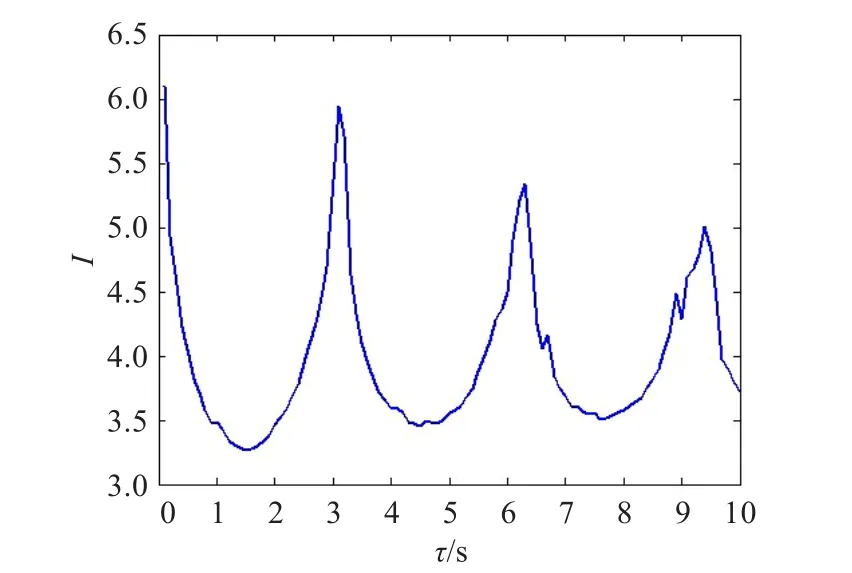
圖2 R?ssler系統互信息函數

正是由于混沌運動的這種偽周期性，為快速尋找最佳的延遲時間τ提供了便利的條件。提出了一種逐步細化的方法來獲得非線性系統互信息的第一局部極小值：首先擴大搜尋的范圍，將延遲時間參考值的間隔步長設置得較大，例如若獲得的時間序列是對R?ssler方程：(a=0.15,b=0.2,c=10)的x分量進行采樣，采樣間隔時間t=0.1 s，共得到4 096個點，那么首先選擇可行的τ值為1 s，2 s，3 s，…，8 s，9 s，10 s，步長為1 s，獲得其互信息函數I與τ的關系如圖3所示。

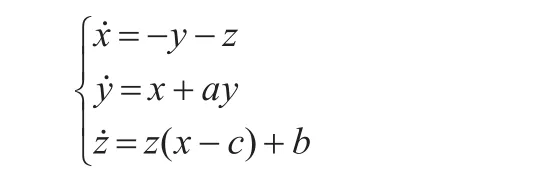
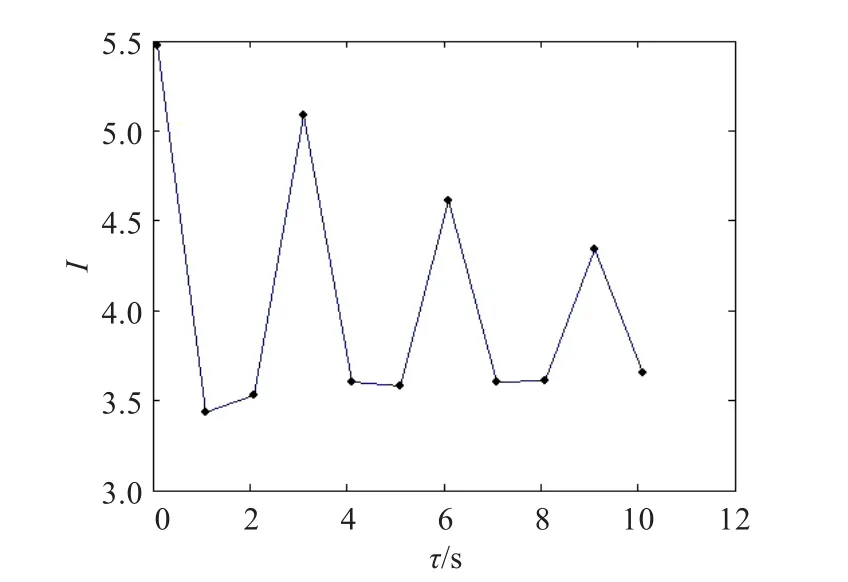
圖3 R?ssler系統互信息函數(τ=0～1 s)

觀察圖3可知，第一個極值區間τ為0～0.2 s，下一步將τ的參考值固定在該區間內，步長縮小為0.1 s，獲得I與τ的關系如圖4所示。

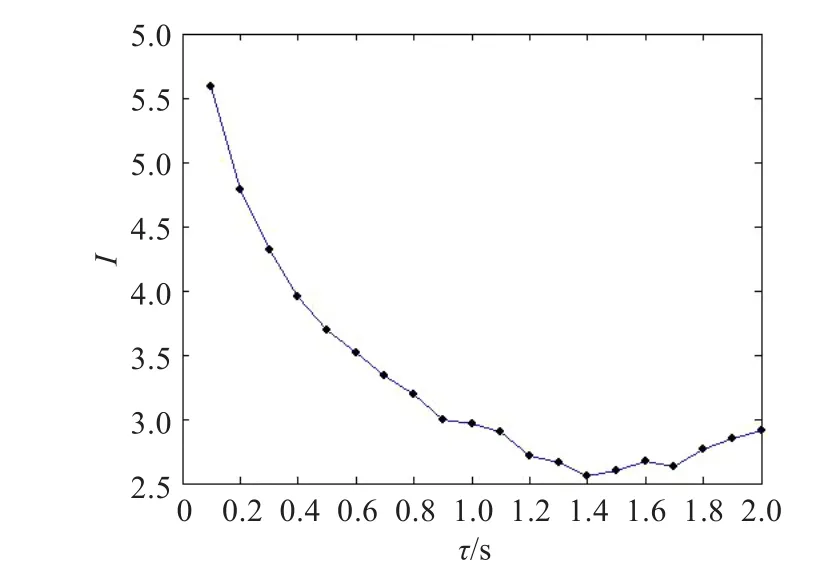
圖4 R?ssler系統互信息函數(τ=0～0.2 s)

由圖4，明顯觀察得R?ssler系統互信息函數的第一局部極小值為τ=1.4，將其作為相空間重構中的延遲時間。為驗證提出算法的可行性，將其運用于Lorenz方程：

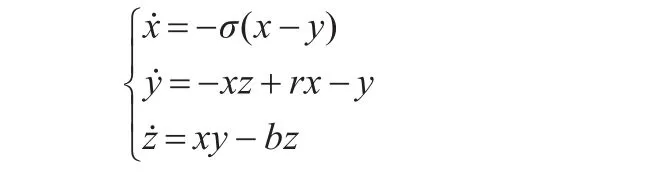
(σ=16,r=45.9,b=4)，采樣間隔時間t=0.01 s，t的取值和非線性系統的非線性程度關系較大，對于非線性較弱的系統，一般取值為0.01；對非線性較強的系統，一般取值為0.001；對于未知的非線性系統，通常先取0.01，如果滿足要求再增加取值，如果不滿足要求，再降低取值。具體步驟如圖5所示。

由圖5結論，取得Lorenz系統重構的延遲時間τ=0.1 s，與以往的結論一致[15]。

4 算法驗證

為驗證算法的有效性和可靠性，根據Takens[2]提出的嵌入定理，對R?ssler和Lorenz系統選取充分大的嵌入維(m=5)，利用互信息函數的第一局部最小值點所確定的延遲時間進行相空間重構，計算關聯維數[3，16]，與理論值進行比較，計算的相對誤差均小于5%，證明了該參數選取的合理性。所得結論如表1所示。

5 結論

根據混沌系統本身具有的偽周期性和各態歷經性，提出采用逐步細化的方法尋找混沌系統互信息函數的第一局部極小值作為相空間重構中的延遲時間。該方法克服了互信息計算繁瑣、耗時較長、難以編程實現等缺點，可以采用遞歸的方法逐步細化，直到τ的選取步長（即精度）縮小到采樣間隔為止，實驗結果表明該算法具有較高的可靠性，大大縮短了搜尋時間與計算復雜度，便于推廣利用。

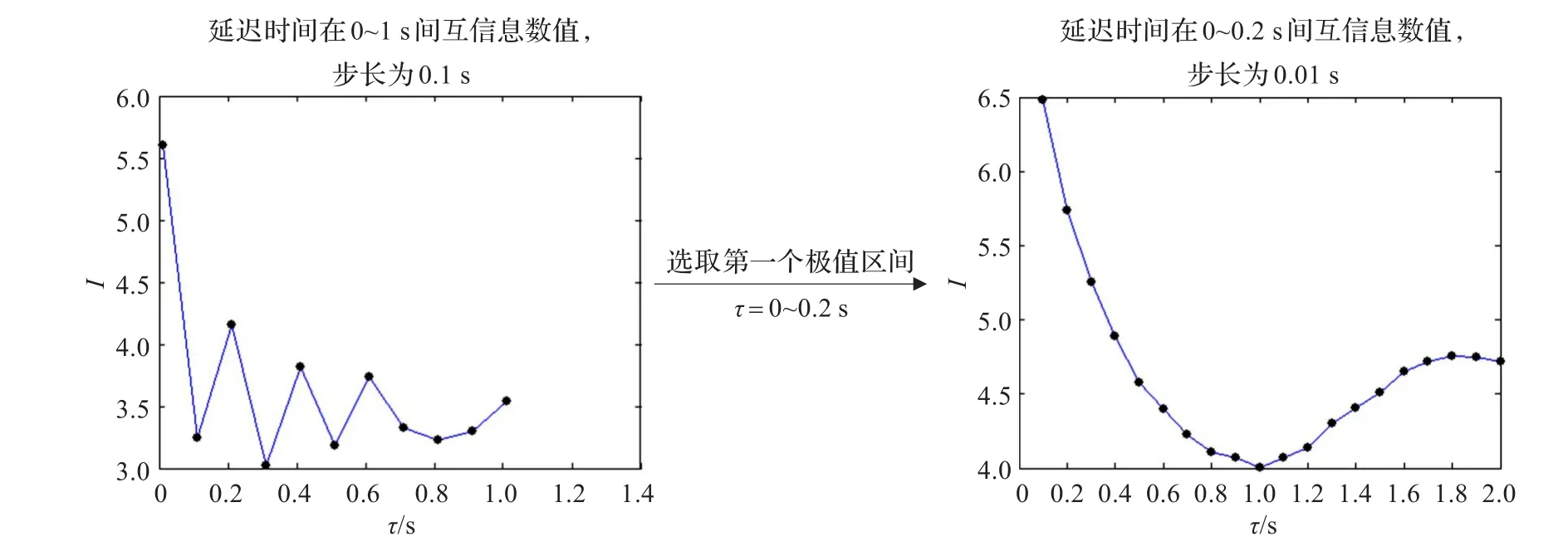
圖5 利用互信息確定Lorenz系統延遲時間流程圖

表1 關聯維數計算結果

[1]劉樹林，張嘉鐘，徐敏強，等.基于小波包與神經網絡的往復壓縮機故障診斷方法[J].石油礦場機械，2002，31（5）：1-3.

[2]Takens F.Detecting strange attractors in turbulence[C]//Rand D A，Young L S.Lecture Notes in Mathematics.New York：Springer-Verlag，1981：366-381.

[3]Castro R，Sauer T.Correlation dimension of attractors through interspike intervals[J].Phys Rev E，1997，55：287-290.

[4]Wolf A，Swift J B.Determining Lyapunov exponents from a time series[J].Phys D，1985，16（3）：285-317.

[5]Gans R F.When is cutting chaotic[J].Journal of Sound and Vibration，1995，188（1）：75-83.

[6]錢蘇翔，焦衛東，楊世錫.基于獨立分量分析的傳感觀測信息融合壓縮方法及其在故障診斷中的應用[J].中國電機工程學報，2006，26（5）：137-142.

[7]李春生，王耀南，陳光輝.基于互信息的組合預測模型及其在電力負荷預測中的應用[J].湖南大學學報：自然科學版，2008，35（9）：58-61.

[8]Albano A M，Muench J，Schwartz C.Singular-value decomposition and the Grassberger-Procaccia algorithm[J].Physical Review A，1988，38（6）：3017-3026.

[9]Rosenstein M T，Collins J J，de Luca C J.Reconstruction expansion as a geometry-based framework for choosing proper delay times[J].Physica D，1994，73：82-98.

[10]Fraser A M，Swinney H L.Independent coordinates for strange attractors from mutual infromation[J].Physical Review A，1986，33（2）：1134-1140.

[11]王海燕，盛昭瀚.混沌時間序列相空間重構參數的選取方法[J].中南大學學報，2000，30（5）：113-117.

[12]周萌清.信息理論基礎[M].北京：北京航空航天大學出版社，1993：11-56.

[13]張菁，樊養余，李慧敏，等.相空間重構中延遲時間選取的新算法[J].計算物理，2011，28（3）：469-474.

[14]劉秉正，彭建華.非線性動力學[M].北京：高等教育出版社，2004：143-150.

[15]Martinerie J M，Albano A M.Mutual information，strange attractors，and the optimal estimation of dimension[J].Phys Rev A，1992，45：7058-7064.

[16]Hentschel H G E，Ocaccia I.The infinite number of generalized dimensions of fractals and strange attractors[J].Physica D，1983，8：433-435.

HE Peng1,ZHOU Deyun1,HUANG Jichuan1，2

1.Electronic Information Institute,Northwestern Polytechnical University,Xi’an 710129,China
2.Military Representative Office of PLA Residing in Chengdu Aircraft Industry Corporation,Chengdu 610092,China

This paper analyzes different methods for determining delay time in state space reconstruction.Although the method of mutual information is more accurate,its computational process is quite cumbersome and time-consuming.So based on the pseudo-periodicity of chaotic attractor,it puts forward a new algorithm to refine delay time step by step using mutual information. The numerical experiment of R?ssler and Lorenz systems proves the reliability of this algorithm.

state space reconstruction;time series;delay time;mutual information;pseudo-periodicity

對比研究混沌時間序列相空間重構中對延遲時間選取的各種算法，根據混沌吸引子所具有的偽周期性與各態歷經的性質，提出采用逐步細化的方法尋找系統互信息函數的第一局部最小值，作為最佳的延遲時間。克服了傳統互信息函數計算繁瑣、難以編程實現的缺點，兼具精確性與高效性。通過R?ssler和Lorenz系統的數值仿真結果驗證了算法的可靠性。

相空間重構；時間序列；延遲時間；互信息；偽周期性

A

TP301.6

10.3778/j.issn.1002-8331.1303-0426

航空科學基金（No.20115553021）。

何鵬（1984—），男，博士研究生，研究領域為智能化指揮與控制工程；周德云（1964—），男，博士，教授，研究領域為預測控制、自適應控制、智能控制理論及其應用、復雜系統建模、航空武器系統工程等；黃吉傳（1980—），男，博士研究生，工程師，研究領域為現代火力控制理論。E-mail：hp17@163.com

2013-03-27

2013-07-29

1002-8331（2013）24-0008-03

CNKI出版日期：2013-09-26http://www.cnki.net/kcms/detail/11.2127.TP.20130926.1645.011.html