基于聲發射檢測技術的轉爐耳軸軸承故障診斷
路俏俏, 黎敏, 陽建宏, 徐金梧, 胡軍
(1.北京科技大學 機械工程學院,北京 100083;2.鞍鋼股份有限公司,遼寧 鞍山 114021)
轉爐是煉鋼生產中的重點設備,耳軸軸承是轉爐傾動機構的重要部分,支撐著爐體、液態金屬、鋼渣、托圈及其附件的全部質量和懸掛減速機的質量,耳軸軸承的工作狀態對保障生產的穩定運行具有重要影響,一旦設備出現事故,將會嚴重影響生產,導致重大經濟損失。所以,對轉爐耳軸軸承的監測具有重大意義。耳軸軸承轉速在1 r/min左右,通常在-95°~190°范圍內進行非連續性旋轉,大部分時間處于靜止狀態,只有在工序需要時進行時斷時續的旋轉[1]。針對耳軸軸承負載重、轉速低、非整周期旋轉且旋轉不連續等工作特點,傳統的振動檢測方法難以進行有效的診斷分析[2-3]。因此,需要針對低速重載設備,研究新的檢測技術和模式識別方法。
聲發射(Acoustic Emission, AE)是材料受外力作用產生變形、斷裂后,以瞬態彈性波形式釋放應變能的現象。對滾動軸承而言,在無故障的狀態下,軸承各組成部分接觸面間的相對運動、碰摩所產生的接觸應力會誘發聲發射信號。此外,由于潤滑不良造成的表面粗糙,以及由于溫度過高、載荷過大等原因而產生的磨損、裂紋、壓痕等故障也會使得滾動軸承在運轉過程中產生聲發射信號[4]。
在滾動軸承故障的早期,由于故障能量比較微弱,不能激起設備表面的振動,利用振動分析方法難以提取設備的早期故障。而聲發射信號來自于缺陷本身,只要有故障存在且處于不斷擴展狀態中,都會以應力波的方式釋放出能量,并能被高靈敏度的聲發射傳感器所接收[5-6]。因此,聲發射檢測技術能夠有效發現設備的早期故障,從而可以利用聲發射信號對軸承的狀態進行監測與診斷分析。
1 軸承聲發射信號的模式識別方法
采集不同狀態下耳軸軸承的聲發射信號,首先計算聲發射特征值,然后利用主成分分析方法進行特征提取,再輸入到最小二乘支持向量機中進行故障識別,最終實現轉爐耳軸軸承的故障識別。
1.1 聲發射的特征值計算
為了客觀描述一個聲發射事件,通常需要計算多個特征值來刻畫聲發射的物理過程。常用的特征值主要包括:幅值、能量、上升時間、持續時間、振鈴計數、均方根值、平均電平等。特征值的計算示意如圖1所示。
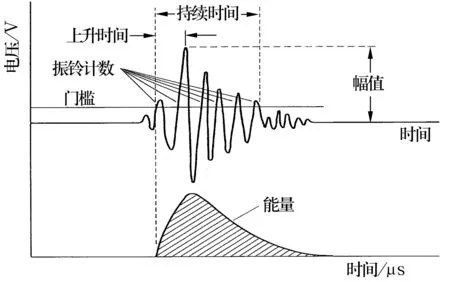
圖1 聲發射特征值的計算示意
從圖1可以看出,幅值實質上是一個聲發射信號的最大值;能量是信號檢波包絡線下的面積,是整個聲發射信號強弱的體現;上升時間是信號第一次越過門檻至最大振幅所經歷的時間;而持續時間則是信號第一次越過門檻值,到幅值最終降至門檻所經歷的時間,主要體現信號的衰減特征;振鈴計數表示越過門檻值的振蕩次數,可以粗略反映信號的強度和頻度;均方根值也稱為有效值,以另一種方式反映了信號的能量大小;平均電平即為信號的平均值。通過上述分析發現,可以通過計算不同的特征值來全面反映一個聲發射事件的本質信息。
1.2 基于主成分分析的特征提取
由于各個聲發射特征值之間存在一定程度的相關性,且高維數據的輸入會增加分類器識別算法的復雜度,降低識別正確率,算法時間也將大幅延長。因此,需要對多維數據進行特征提取。主成分分析法是一種多變量分析方法,主要目的是對多變量數據進行最佳綜合簡化,即在保證數據信息丟失最小的原則下,對高維數據進行降維處理,把原來存在內在關聯的變量變為不相關的若干新變量,而這些新的變量將攜帶盡可能多的原始數據信息,從而實現數據的特征提取。
假設X是一個n×m的數據矩陣,其中的每一列對應一個聲發射特征值,每一行對應一個聲發射樣本。首先,將X進行標準化處理為E,即按列分別減去均值除以標準差;其次,計算標準化數據E矩陣的協方差矩陣ETE;再求取協方差矩陣ETE的特征值λ1≥λ2≥…≥λm和對應的特征向量P1,P2,…,Pm;然后計算特征能量
(1)
如果當前h個特征值的和超過全部m個特征值總和的80%,則認為所對應的前h個特征向量保留了原信號中的絕大部分信息,則計算得到主成分為
tj=E·Pj,j=1,2,…,h。
(2)
將這h個主成分tj構成新的特征值矩陣Xn×h,并作為分類特征輸入到分類器中進行模式識別。
1.3 基于最小二乘支持向量機的特征識別
支持向量機(Support Vector Machine,SVM)是目前有效解決小樣本、非線性和高維數據問題的新型機器學習方法。假設給定線性可分的樣本集(Xi,yi),i=1,2,...,n,n表示樣本的個數,yi∈{-1,1}。以兩類分類問題來說明SVM的核心思想。首先要獲得一個最優分類面,不僅能將兩類樣本正確區分,而且要使分類間隔最大,即需滿足
yi[(w·Xi)+b]≥1,
(3)
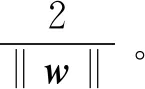
支持向量機的訓練速度慢和難以大規模運算是制約其發展和推廣的重要原因。作為經典支持向量機方法的發展和改進,最小二乘支持向量機(Least Squares SVM,LS-SVM)采用等式約束替代不等式約束,求解過程變成解一組等式方程,避免了求解耗時的二次規劃問題,求解速度大大加快[7]。
LS-SVM以最小二乘線性系統為損失函數,代替SVM采用的二次規劃方法。通過求解線性方程組保證‖w‖2最小化,獲得最優分類面,即需滿足
(4)
式中:φ(Xi)為非線性變換函數;允許錯分的松弛變量ηi∈Rn;γ為可調正則化參數,控制對超出誤差樣本的懲罰。為求解上述優化問題,把約束優化問題變成無約束優化問題,定義Lagrange函數
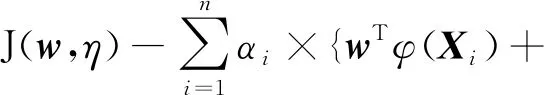
b+ηi-yi}。
(5)
分別求L對αi,w,b,ηi的偏導數,聯立求解方程后,可得到最優分類函數
(6)
式中:K(X,Xi)為核函數,常用的核函數有線性核、高斯核、徑向基核等,核函數的選擇與分類效果密切相關。
(6)式實質上可以看作是一個分類模型。首先利用大量樣本進行訓練,目的是要獲得模型中的各個系數。當新來一組待識別的樣本集時,進行相應的特征值計算和PCA特征提取后,可以直接輸入分類模型中,實現聲發射信號的模式識別。具體流程如圖2所示。
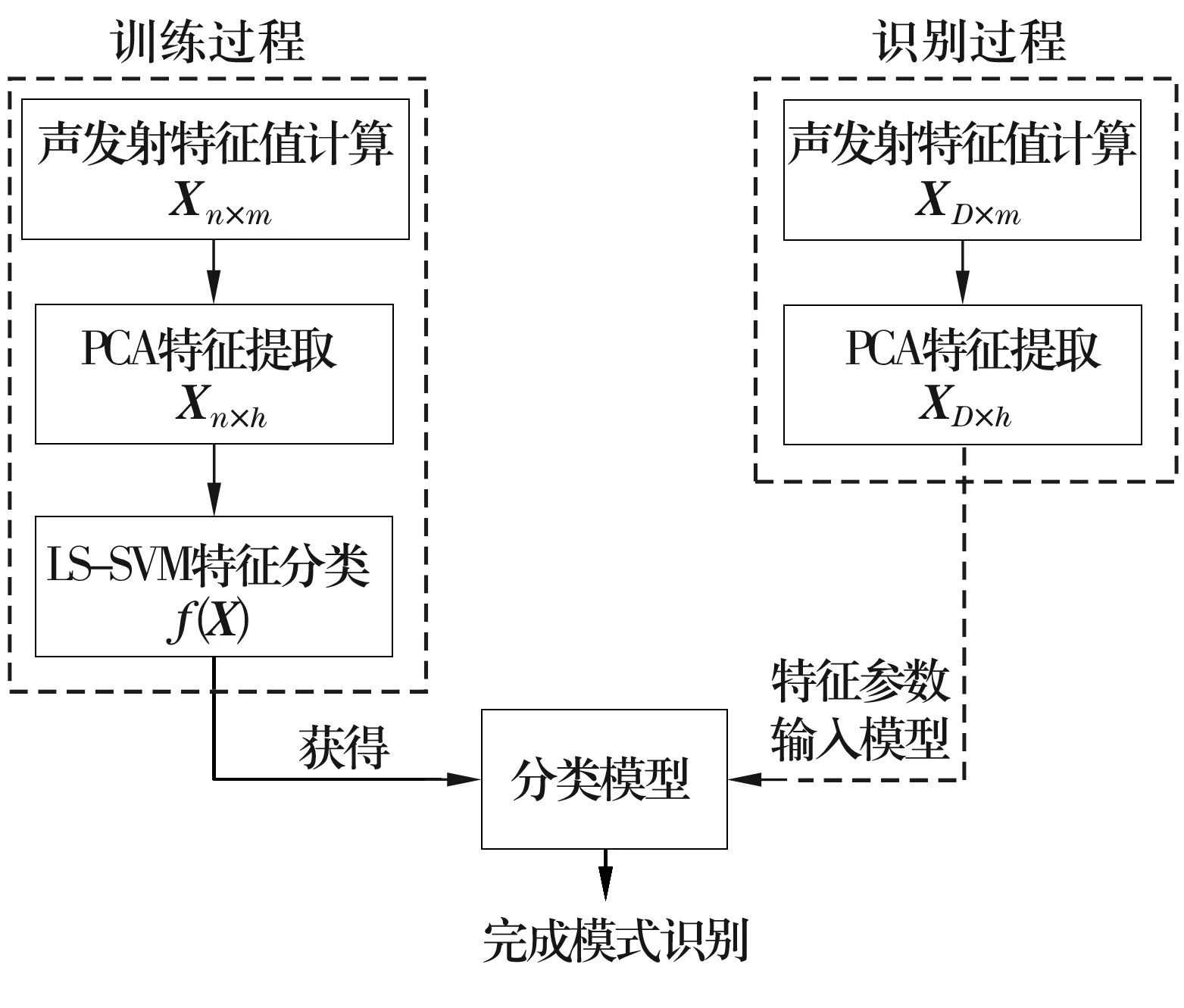
圖2 聲發射信號的模式識別流程
2 試驗驗證
利用美國PAC公司的SAMOS聲發射儀對某鋼廠容量均為260 t的A,B兩個轉爐從動側的耳軸軸承進行聲發射信號采集。軸承以1 r/min左右的速度做非整周期、非勻速旋轉。將聲發射傳感器分別安裝在軸承座承載區的45°方向,如圖3所示。采樣頻率500 kHz,連續采集30 s內空爐搖爐狀態下聲發射信號。利用A,B爐各600個聲發射樣本進行訓練,各300個聲發射樣本用于測試。參與訓練的樣本的各個特征值曲線如圖4、圖5所示。
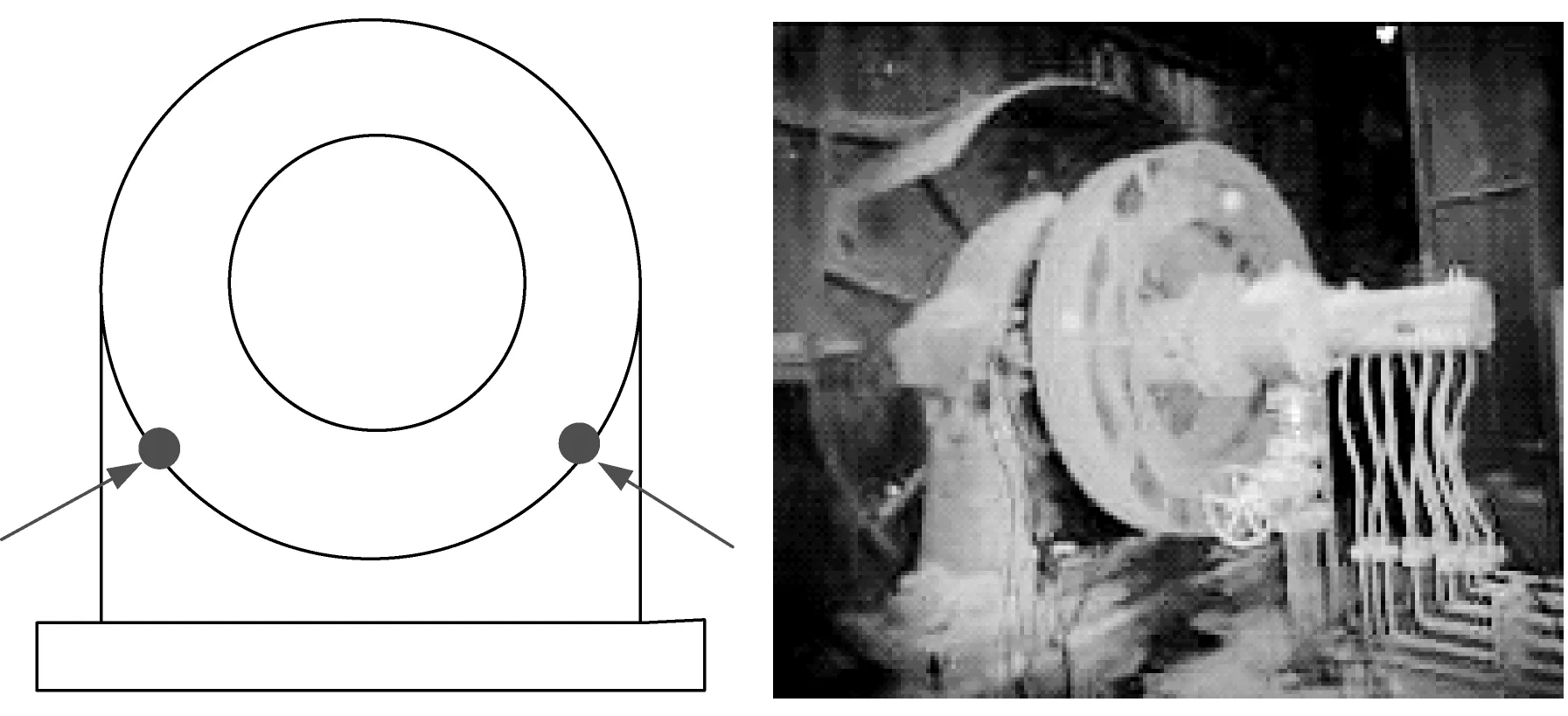
圖3 轉爐耳軸軸承測點布局圖
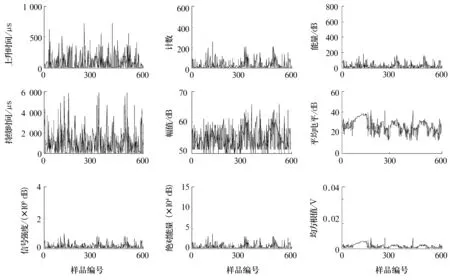
圖4 A爐訓練樣本的特征值曲線
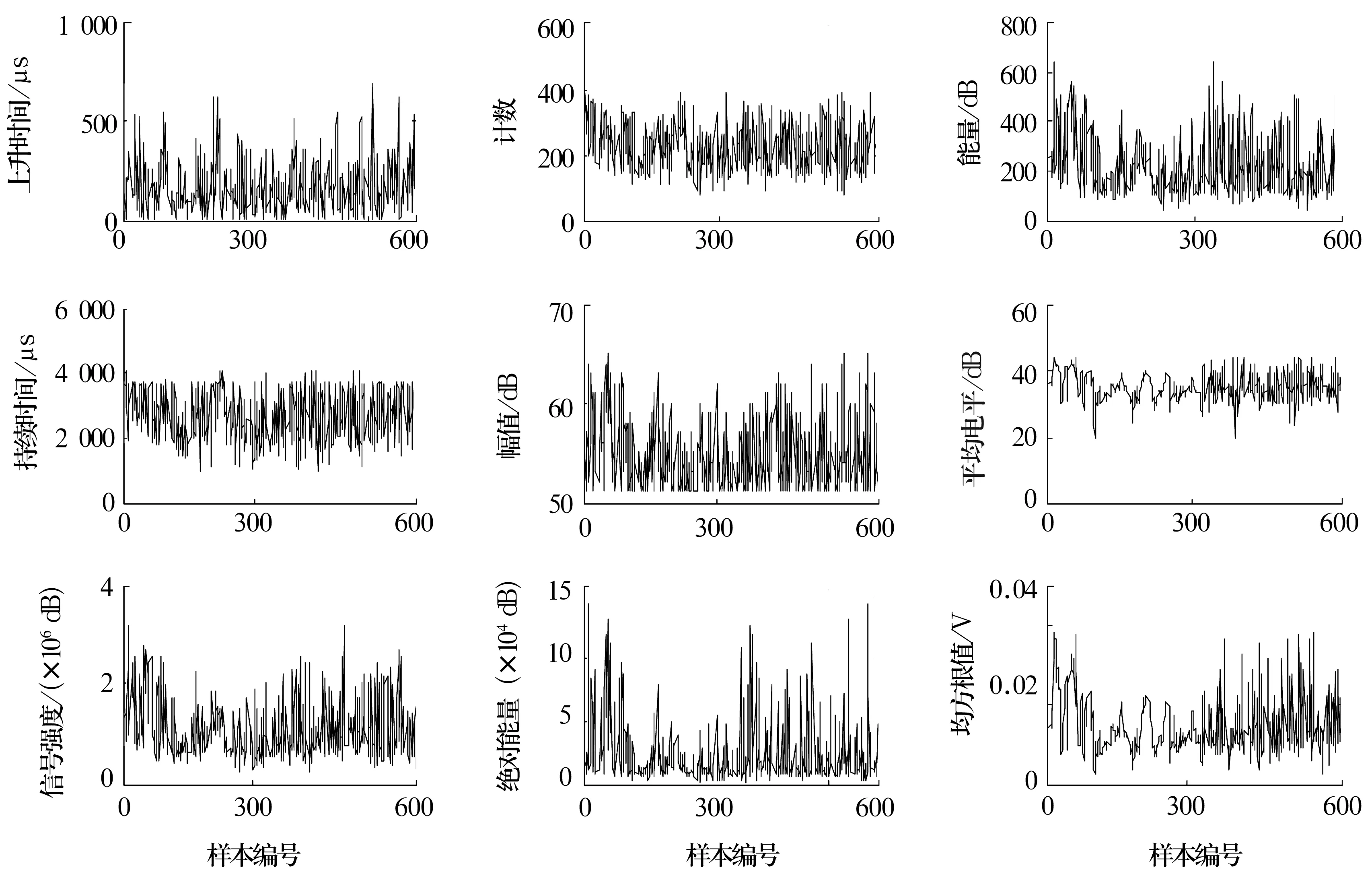
圖5 B爐訓練樣本的特征值曲線
從圖中可以看出,B爐的特征值普遍高于A爐的特征值,可以初步判斷A爐的狀態優于B爐的狀態。但當新來一組樣本時,該如何判斷其狀態的好壞是進行故障診斷的關鍵。因此,需要研究分類識別的算法來進行故障診斷。首先,利用主成分分析方法對圖中的9個特征值進行特征提取,當取h=3時,可滿足(1)式的要求,將9個特征值融合為3個綜合參量,這3個綜合參量保留了原信號中80%以上的信息,可將它們輸入到分類器中進行模式識別。
為了評價分類識別的效果,需要定義一個評價指標以反映分類器對數據集分類識別的平均性能。用總體正確率表示為
(7)
式中:TA為A類樣本中被準確識別為A類的樣本個數;FA為A類樣本中被誤識別為B類的樣本個數;TB和FB以此類推。
為驗證本文方法的有效性,設計了3個試驗,見表1。
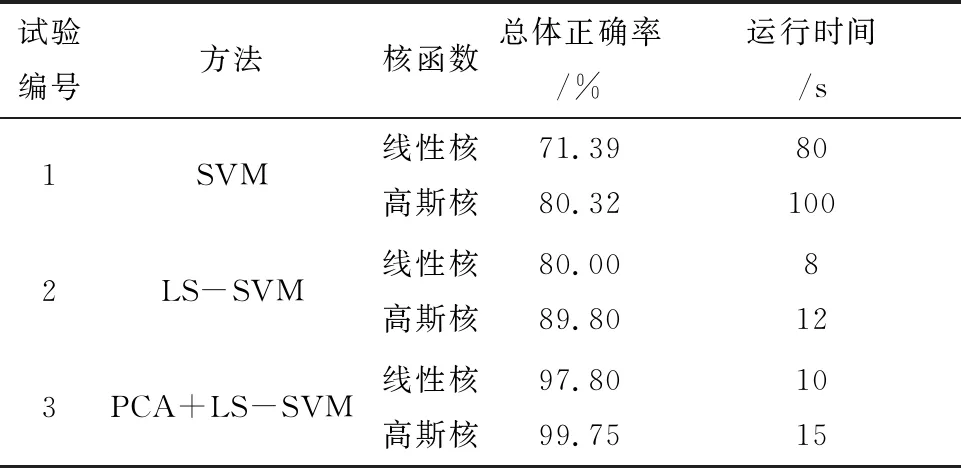
表1 轉爐耳軸軸承分類識別結果
比較試驗1與試驗2的結果可以看出:運用LS-SVM新的模式識別方法,核函數為線性核時,可以將傳統SVM方法的總體正確率從71.39%提高到80%,且運行時間縮短為原來的10%,當使用高斯核函數時,也有類似的結論。
比較試驗3和試驗2的結果可以看出:利用PCA方法進行特征提取后,再輸入到LS-SVM分類器中進行模式識別,總體正確率進一步提高到97.8%。更重要的是,在試驗3中可以看出:通過PCA降維處理后的數據,使用線性核函數與使用高斯核函數的總體正確率非常接近。而在試驗1和試驗2中,使用不同的核函數的總體正確率卻有近10%的差距,說明使用PCA進行特征提取后,不必再使用復雜的高斯核函數,使用線性核函數就可同樣得到較高的總體正確率,這樣不僅降低了算法的復雜度,也縮短了算法的運行時間。
經過現場油液分析的驗證,A爐耳軸軸承處于正常狀態,而B爐耳軸軸承存在磨損現象。為進一步說明方法的有效性,以線性核函數為例,給出了利用試驗3的方法對兩類樣本分類的結果,見表2。

表2 試驗3的分類結果
從表2可以看出,對正常狀態的樣本分類正確率為99%,對磨損狀態的樣本分類正確率為96.6%,說明所設計的分類器能夠較準確地識別出兩種不同的軸承狀態。
3 結論
(1)針對轉爐耳軸軸承低速、重載、非整周期、間歇旋轉的工作特點,采用聲發射技術對耳軸軸承進行狀態監測是一種新監測技術的有益嘗試,可以為具有類似工作特點的設備提供參考。
(2)將PCA特征提取方法和LS-SVM分類方法相結合,對正常和磨損狀態下的轉爐耳軸軸承進行故障識別,在使用線性核函數數時,總體正確率可達到97.8%,且算法復雜度低,運算速度快,可為轉爐耳軸軸承的在線監測與故障診斷提供有力支持。

