氣象測試系統現場校準誤差

劉紅霞 ， 黃 玲 ， 蔣 惠

（1.成都信息工程學院，四川 成都 610225；2.塔城地區氣象局，新疆 塔城 834700；3.呼圖壁縣氣象局，新疆 昌吉 831200）

0 引 言

在氣象測試中離不開壓力、溫度、濕度、風向的測量，為滿足氣象高精度測試的要求，通常配備了大量的數據測量、采集系統。對其實施準確的校準是控制測試系統準確度的主要途徑，也是保證測試數據準確可信的必要手段。

1 國內外進展情況

其實，國內外早就有“現場校準”的做法，但由于當時準確度低，在現場主要檢查儀器、儀表是否正常，還不能用來校準工作特性，也沒有“現場校準”的說法。

由于現場的環境條件和計量室的環境條件不一樣，使得在計量室校準獲得的工作特性不能滿足現場實際工作條件的需要，從而促進對實際工作環境和工作條件的現場校準技術的研究，尤其對現場校準儀的溯源和校準規范問題的解決。近年來，隨著ISO 9000標準的貫徹，提出了從產品研制生產過程中，從設計、研制、生產試驗和使用過程中都要實施“計量保證”的措施。現場校準就是測試儀表在使用過程中實施“計量保證”的有力措施之一。

2 測量誤差

2.1 測量誤差源

測試系統的每個測量環節都可能存在著測量誤差，造成測試系統與測量通道的基本誤差源可分為：

（1）校準誤差源；（2）數據采集誤差源；（3）數據處理誤差源。

2.2 測量誤差的分類

按照測量結果中存在誤差的特點與性質不同，測量誤差可分為系統誤差、隨機誤差和粗大誤差。需說明的是，雖可將誤差分為3類，但各類誤差在一定的條件下可以相互轉換。

3 測試系統的靜態特性與數據處理

3.1 概述

測試系統與其輸入、輸出之間的關系如圖1所示，其中x和y分別表示輸入量和輸出量，H（t）表示系統的傳遞特性，3者之間一般有如下3種關系：

圖1 測試系統框圖

（1）若已知輸入量和系統的傳遞關系，則可求出系統的輸出量；

（2）已知系統的輸入量和輸出量，則可知道系統的傳遞特性；

（3）已知系統的傳遞特性和輸出量，來推知系統的輸入量。

測試系統的輸出量y和輸入量x之間的函數關系如式（1），這一關系和時間無關，通常可以描述為

式中：ai——測試系統的標定系數，反映了系統靜態特性曲線的形態。當式（1）寫成

時，系統的靜態特性為一條直線，稱a0為零位輸出，a1為靜態傳遞系數（或靜態增益）。通常測試系統的零位是可以補償的，使系統的靜態特性變為

這時稱測試系統為線性的。

3.2 測試系統的靜態標定

靜態標定就是將原始基準器，或比被標定系統準確度高的各級標準，或已知輸入源作用于測試系統得出測試系統的激勵——相應關系的試驗操作。

標定的主要作用是：

（1）確定測試系統的輸入－輸出關系，賦予測試系統分度值；

（2）確定測試系統的靜態特性指標；

（3）消除系統誤差，改善測試系統的正確度。

通過標定，可得到測試系統的響應值γi和激勵值xi之間的對應關系，稱為測試系統的靜態特性，可以用一個多項式表示，即

式（4）稱為測試系統的靜態數學模型。靜態特性可用一條曲線表示，該曲線稱為測試系統的靜態特性曲線，有時也稱靜態校準曲線或靜態標定曲線，一般都以平均特性曲線作為測試系統的靜態特性。

3.3 測量不確定性的數學模型

測量的不確定性用不確定度表示：用測量的系統誤差和精密度（表征測量結果中隨機誤差大小的程度）的合成表示。不確定度按其數值評定方法的不同分為A、B兩類。計算使用“疊加”和“方根和”兩種數學模型（建議采用置信概率為95%）。

（1）疊加模型：

U=B+Ur（置信概率為99%）

4 現場校準

4.1 校準目的

提高測試參數的準確度，并使測試參數可溯源到國家標準或國際標準。如實際現場測試系統的測量精度要求高（比如壓力、溫度、濕度測量），此時，地方校準標準不能滿足預期要求，則現場使用的工作標準直接越級溯源到行業標準或國家最高標準。但值得注意的是，在估算該項測量系統的校準溯源鏈誤差時，誤差源則為國家標準減去現場工作標準或行業標準減去現場工作標準。

4.2 信號接入方式

在現場校準各類測量通道時，一般接入的為物理信號源（標準信號源），然后對包含傳感器或變送器在內的各個測量環節組成的測試系統進行校準。

4.3 測量誤差計算

4.3.1 校準誤差

校準誤差是測試系統的主要誤差，通過校準（檢定）可測得系統的主要誤差值而予以修正。

（1）平均值計算

正行程平均值：

（2）回程誤差計算

（3）校準系統誤差分量的計算

（4）實際校準偏差的計算

對呈正態分布的重復測量數據，按式（10）進行計算：

（5）校準隨機誤差的計算

對正態分布隨機誤差不確定度上限的計算公式為

式中：t95——學生氏分布的“t”因子，在置信概率為95%重復測量次數n=50（自由度μ=n-1）時，由t 分布，可查 t95≈2；

s——標準偏差，按式（10）計算的實際值代入。

4.3.2 數據采集和數據處理誤差

數據采集和數據處理誤差視其測量通道種類和測量環節組成的不同，來具體確定誤差種類和數量。但是，環境影響誤差和安裝方法影響誤差產生的附加誤差分量均是存在的，必須認真分析確定。

4.4 誤差的合成

4.4.1 系統誤差分量的合成

對于各相對獨立的系統誤差分量Bij，可用“方和根”方法進行合成。

當未修正的系統誤差呈均勻分布時，應在標準“方和根”方法合成的基礎上，對合成后的系統誤差乘上k倍的范圍因子，即得合成后總的系統誤差。

式中：k——范圍因子，當置信概率為95%，取k=1.1，如果未修正得系統誤差呈均勻分布，取k=1，本報告取k=1.1；

i——在j類誤差中第i種誤差；

j——測試系統誤差類別；

ΔBij——第j類、i類系統誤差分量絕對值。

4.4.2 隨機誤差分量得合成

對各種隨機誤差分量（ΔUr）ij2，可用“方和根”方法進行合成。

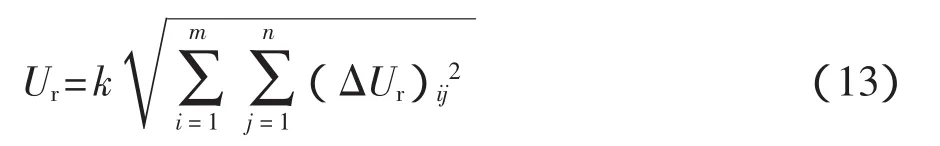
式中：（ΔUr）ij——第j類、i種隨機誤差分量絕對值。4.4.3 測量結果的相對誤差極限

4.5 系統附加誤差分量的計算

（1）在校準系統中已包括得測量環節不再參與計算，只是在數據采集中的小環節引起得附加系統誤差分量仍需逐一計算。

（2）原則上，把那些數值固定或遵循一定規律變化的誤差，以及環境溫度變化和時間漂移引起系統增益和零漂等附加誤差，均可視為系統誤差分量。而把那些無規律可循或隨機變化的誤差，如系統或測量環節的測量不重復性誤差、干擾、噪聲誤差等視為隨機誤差分量。

5 結束語

本文初步探討了氣象專業測試系統校準的原理以及測量誤差評定的方法，該方法能夠比較容易在現場得到實施和運用，對于提高測試系統的測試可信度有較大幫助，實踐證明該方法具有較高的合理性與先進性。

[1]JJG 1048—1995數據采集系統校準規范[S].北京：中國計量出版社，1995.

[2]趙慶海.測試技術與工程應用[M].北京：化學工業出版社，2005.