電阻法測量繞組溫升數據處理的方法及應用

韓強 黃柱鋒 陳鏡亮

（東莞出入境檢驗檢疫局 廣東東莞 523071）

1 引言

溫升試驗是家用電器、變壓器、電動工具等電子電器產品的重要檢測項目，是測定電器產品在規定條件下，例如：接線端子、外殼、觸頭、手柄、繞組等零部件的發熱溫度與環境溫度的差值，是否符合相應標準規定的溫升限值的檢測項目；是評價產品元氣件、絕緣材料部件質量，考核電器產品防止火焰蔓延、防止灼傷以及整體電氣安全，以及是否對使用者或周圍環境產生危險的關鍵項目。

在對繞組進行的溫升試驗中，常用的測量溫度或溫升的方法，除了電阻測溫法之外，還有紅外線測溫法，熱電偶測溫法。但是，熱電偶法、紅外線法都局限于被測樣品的表面，以及由于測溫點選定的隨機性，不能真實的反應內部溫度；電阻測溫法由于其準確度高，可以通過計算得到線圈內部的溫度而廣泛應用。

2 電阻法測量溫度的基本原理

電阻法是根據銅、鋁等金屬其電阻隨溫度變化呈現某一規律的特性，通過繞組在發熱時電阻的變化，來計算繞組的溫度。具體方法是利用繞組的直流電阻，在溫度升高后電阻值相應增大的關系來確定線圈的溫度，其測得是繞組溫度的平均值。在一定的溫度范圍內，變壓器繞組的電阻值將隨著溫度的上升而相應的增加，而且其阻值與溫度之間存在著一定的函數關系。

繞組的溫升值按照以下公式計算：

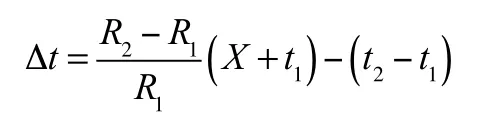
式中：

△t——高于t 的溫升，最高溫度為△t+t；

R——在環境溫度為t時，試驗開始時的繞組電阻，單位是歐姆；

R——當達到穩定狀態時，試驗結束時的繞組電阻，單位是歐姆；

X——對于銅線繞組為234.5，對于鋁線繞組為225；

t——試驗開始時的環境溫度，單位是攝氏度；

t 試驗結束時的環境溫度，單位是攝氏度；

試驗開始時，繞組的溫度應等于環境溫度。

冷態時的電阻R (試驗開始測得的電阻)和熱態時的電阻R (試驗結束測得的電阻)必須在被測繞組同一出線端測得。

要精確測量線圈電阻，只能使用高精度的數字電橋。而數字電橋只能在被測繞組斷電的環境下才能開展測量，它對電流非常敏感，繞組從電源斷開后還需短路幾秒鐘(實際操作一般是5秒)再接到電橋上測電阻，以避免殘余電量燒壞電橋。

由于這個原因，我們沒辦法得到繞組斷電瞬間To時的線圈電阻值R ，因此，只能通過間接的方法來得出R ，即根據繞組導體電阻隨溫度變化呈現某一規律的特性，推算出斷電瞬時的電阻值R ，就可推算出線圈溫升△t。繞組斷開電源后，其溫度逐漸下降，所以測得的電阻值并不是線圈斷電瞬時的電阻值，我們可以通過短時間等間隔讀取的電阻測量值，利用作圖法和回歸分析法來確定斷電瞬時的電阻值，從而推算出繞組溫升。

3 繞組斷電瞬時的電阻值R的確定

確定斷電瞬時的電阻值R一般有兩種方法：作圖法和回歸分析法。

3.1 作圖法

作圖法是在直角坐標系上畫出“電阻—時間”的相關曲線，然后通過相關曲線來確定斷電瞬時的電阻值R 。為了能準確繪制電阻與時間變化的曲線，測量次數應在10次左右，而且第一個測量值越快，測試準確度越高，作圖法比較直觀。用作圖法處理數據時，我們通常采用的是“目測法”，這種方法雖然簡單明了，易學易用，但常常受人為因素影響較大，即使對同一組數據來說，不同的人員也會得出不同的結果來。因此， 該方法只在進行快速估算的情況下使用。對于檢測實驗室，不推薦使用此種方法。

3.2 回歸分析法

所謂回歸分析法，是在掌握大量觀察數據的基礎上，利用數理統計方法建立因變量與自變量之間的回歸關系函數表達式（稱回歸方程式）。

具體在電阻法測量繞組溫升的實際應用中，是根據多次測量的繞組斷電后時間及與其對應的繞組電阻值，再結合一些數理統計方面的知識，運用回歸分析的方法，在數學上嚴格地確定電阻與時間的相關曲線，最后找出斷電零時刻的電阻值。

在回歸分析中，當研究的因果關系只涉及因變量和一個自變量時，叫做一元回歸分析；當研究的因果關系涉及因變量和兩個或兩個以上自變量時，叫做多元回歸分析。此外，回歸分析中，又依據描述自變量與因變量之間因果關系的函數表達式是線性的還是非線性的，分為線性回歸分析和非線性回歸分析。通常線性回歸分析法是最基本的分析方法，遇到非線性回歸問題可以借助數學手段化為線性回歸問題處理。

3.2.1 一元線性回歸方程

一般地，用線性函數a+bx來估計Y的數學期望的問題，稱為一元線性回歸問題。稱方程

為Y的關于x的線性回歸方程。稱斜率b為回歸系數。對于x的每個值，設：

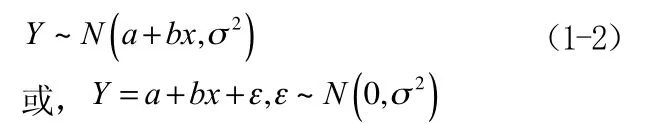
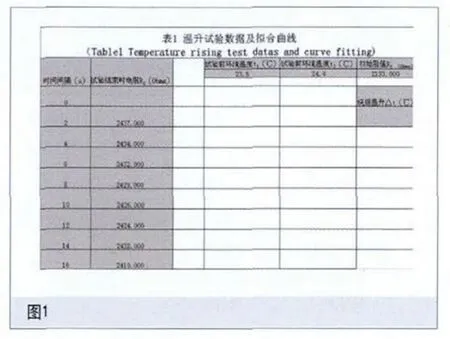
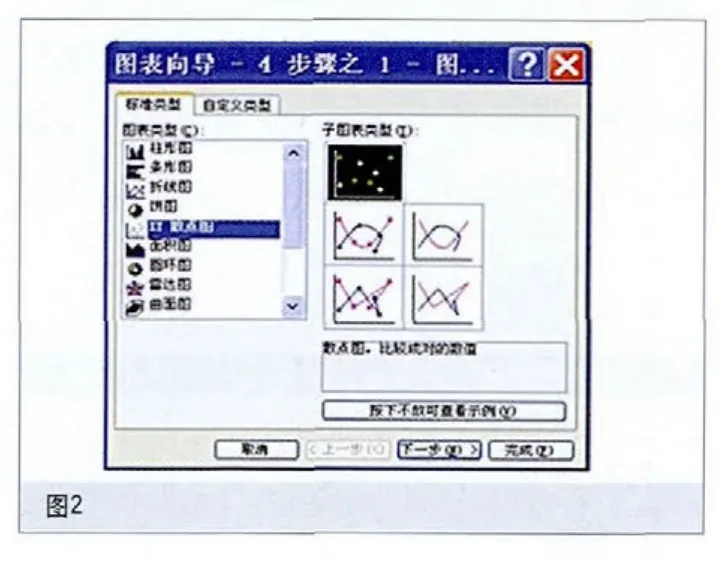
其中a,b,σ是與x無關的常數。對于已知數據(x,y) (i=1,2,…,n) ，用最小二乘法來估計a和b，離差平方和：

為了使Q取得最小值，將Q分別對a和b求偏導數，并令它們等于零，得

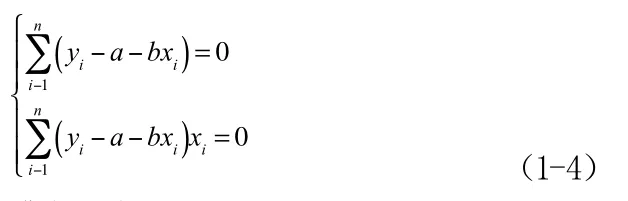
或者寫成

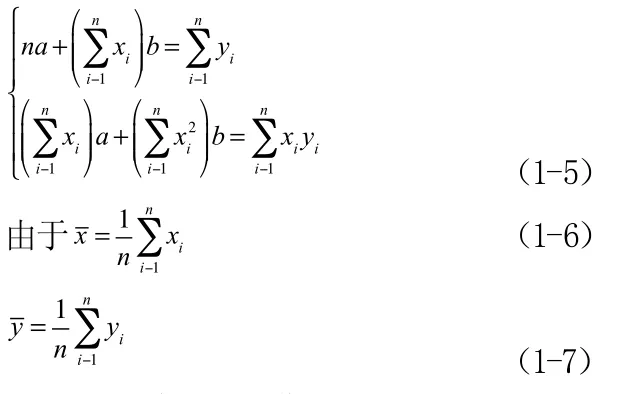
則（1－5）式可以寫作

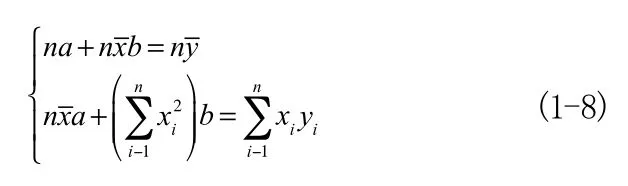
方程組（1-8）稱為正規方程組，該方程組有唯一的一組解

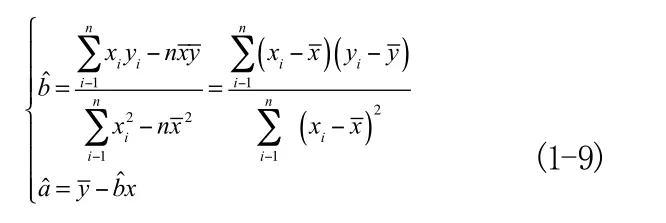
記:

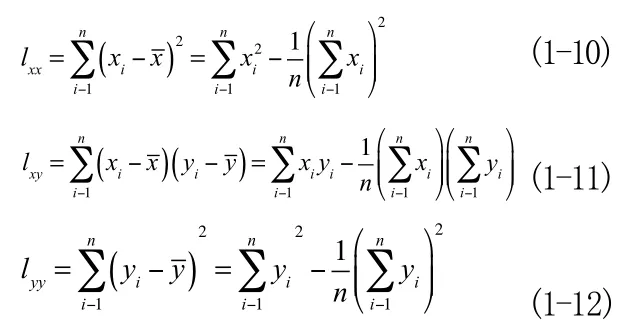
分別成l 和l 為x和Y的離差平方和，稱l 為x和Y的離差乘積和。則有

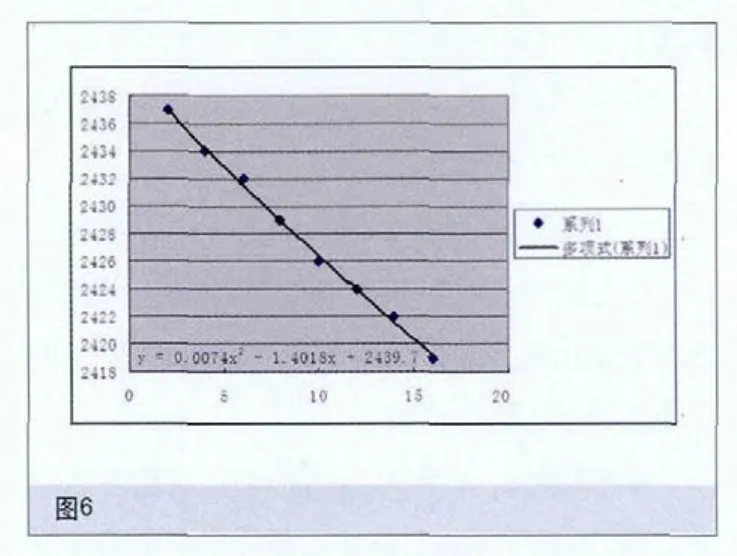
將（1－13）代入到回歸方程（1-1）中,則得到經驗回歸方程

3.2.2 一元非線性回歸方程

上節討論的回歸分析與回歸模型都假定是線性的，而在使用“電阻法測溫升”通過作圖法發現測得的數據并不是線性分布的，因此，為了得到準確的數據，我們需要建立的一元多次非線性回歸模型。由于線性回歸方程比較簡單，所以在遇到非線性模型時，最好將其轉換為線性模型。

由此可見，求一元多次的多項式回歸的問題就轉化為多元線性回歸模型。具體可參考相關數學書籍。通過實踐證明，一元多次回歸求出的R值比一元一次回歸要更接近真實值，而且次數越高，數值越精確。為了減少計算量，在滿足試驗精度要求的情況下，一般推薦使用一元二次方程來求R值。

4 Excel軟件在數據處理中的應用

隨著計算機應用日益普及，用Excel軟件處理實驗數據已經逐步推廣。Excel軟件在實驗數據曲線(直線)方程擬合、作圖、計算公式值和常用函數值、計算測量列平均值、標準偏差和不確定度等都有獨特的功能。利用Excel軟件圖表功能可以很方便對實驗數據作圖,并對測量點添加趨勢線,得擬合曲線函數關系式，實現對檢測數據的回歸分析。

下面就介紹一下利用Excel的繪制散點圖功能，對數據進行曲線擬合及生成該組數據函數方程的過程。假定在變壓器溫升試驗中獲得表1數據。

(1)根據上組數據新建一張Excel數據表，輸入試驗數據，并選中，如圖1。

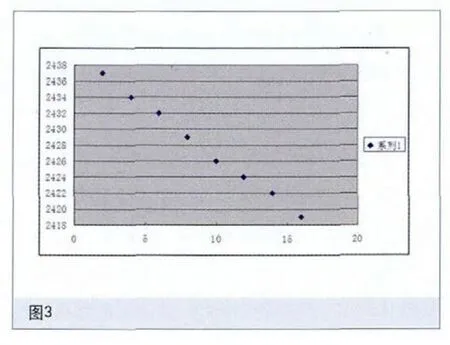
(2)在“插入”欄中選擇“圖表”，屏幕上顯示如圖2所示的”圖表向導”，然后選“XY散點圖”連續按下一步，完成“圖表向導”4步驟。在表格中就會顯示如圖3所示的曲線圖。

(3)在所得的曲線上擊右鍵，選中“添加趨勢線” 然后如圖4所示，在“類型”框中選擇“多項式”，并在“階數“欄中確定階數，在滿足試驗精度要求的情況下，一般設定為2階。

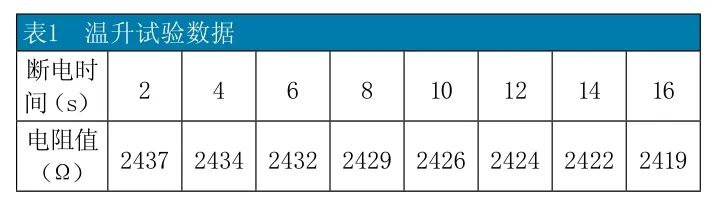
表1 溫升試驗數據斷電時間（s） 2 4 6 8 10 12 14 16電阻值（Ω） 2437 2434 2432 2429 2426 2424 2422 2419

(4)在“添加趨勢線“的”選項“框中，選中”顯示公式“(圖5)，再按確定，曲線擬合就完成了，擬合好的公式圖6所示，顯示在曲線圖圖6上。

(5)根據顯示的公式

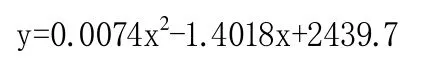
可計算出當斷電瞬間T=0s即x=0時，繞組電阻y=2439.7Ω。

5 結束語

由此可見，電阻法測量繞組溫升的方法和精度都會對產品的合格性評定產生決定性的影響，很多產品都會因為在涉及溫升的測試中出現問題。利用Excel的可繪制散點圖的功能，實現對檢測數據的曲線擬合，數據處理準確、直觀、快捷、簡易。

[1]謝秀杰.電阻法測溫的原理及數學計算[J].電子質量.2008年第12期

[2]張紅飚.電阻變化法測量繞組溫升的探討[J].福建分析測試.2005年第3期

[3]IEC61558-1:2005+A1:2009，Safety of power transformers, power supplies, reactors and similar products Part 1: General requirements and tests [S].

[4]GB 19212.1-2008, 電力變壓器、電源裝置和類似產品的安全 第1部分：通用要求[S].

[5]何曉群，劉文卿.《應用回歸分析》第二版[S].

[6]盛驟等.《概率論與數理統計》[S].