導熱反問題在身管傳熱中的應用

陳 剛，周淵鍵，吳 斌

(解放軍陸軍軍官學院 a.機械工程教研室;b.研究生管理大隊1 隊;c.裝甲兵系，合肥 230031)

導熱反問題是相對導熱正問題而言的一個交叉學科，它涉及傳熱學、物理學、數學、計算機、實驗技術等眾多的領域，在實際工程中有著廣泛的應用前景［1-5］。

導熱反問題在各領域中有著廣泛的應用背景，但其非適定性、非線性、計算量大等特點，使得求解比較困難［6-8］。導熱反問題作為一個優化問題，已有一些求解方法，如基于梯度的優化方法Levenberg-Marquardt 算法、遺傳算法、貝葉斯方法等［9-11］。

文中以對火炮發射時內膛熱交換過程的分析，基于導熱反問題的研究方法，根據Levenberg-Marquardt 算法建立由結構內部一個或多個溫度測點的測量值計算內膛壁溫度與熱流密度的數學模型。

1 導熱正問題

模擬三維水平火炮身管物理模型如圖1 所示，內徑為50 mm，外徑70 mm，長200 mm。本文中假設xoy 面為對稱面，水平身管上下熱工情況相同，因此只取水平身管的一側進行討論。水平身管的內外壁分別為第一類與第三類邊界條件，其控制方程及邊界條件為:

本文使用有限單元法求解導熱問題，采用八節點六面體等參單元離散模型，如圖1 所示。在內壁邊界條件及身管導熱系數已知情況下，求解導熱正問題，獲得身管內壁溫度場。式(1)～式(5)構成三維火炮身管瞬態導熱初邊值定解問題。已知內外壁邊界條件及初始溫度，即可計算出身管隨時間變化的溫度分布。

圖1 網格模型

2 導熱反問題

在求解導熱正問題時，內外壁邊界條件已知，需要求解的未知量為外壁面的溫度;而在進行反問題分析時，內壁面的溫度分布為未知參量，需要根據外壁面的測量溫度，利用反演算法求得。

本文待反演的參量為身管內壁面的溫度分布，屬于函數估計問題。Su 等借鑒有限單元法中單元形函數的思想，把反問題中的函數估計轉化為參數估計問題。本文亦用此法，把內壁溫度場的反演轉化為內壁有限結點溫度的反演。

在水平身管內壁面的軸向方向，溫度值為

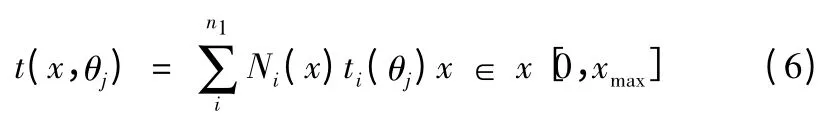
式中:t(x，θj)為在橫坐標為x 的橫截面上ti(θj)為身管內壁面圓周方向上θj角處的溫度值，為已知值，在反問題分析中為待反演參量;Ni(x)為身管內壁軸向上的形函數，本文算例中采用線性插值函數，類似地，在水平身管內壁面圓周方向，溫度值由式(7)確定

本文研制的是一種無機泡沫吸波材料，是利用碎玻璃或火山灰等為主要原材料，在其中添加電磁損耗物質，熔融發泡而成的一種隱身材料，如圖7所示。

式中:t(xj，θ)為橫坐標為xj的橫截面是θ 角處的溫度值，θ為變量;ti(xj)為管內壁橫坐標為xj的橫截面上的溫度值，為已知值，在反問題分析中為待反演參量;Ni(θ)為身管內壁圓周上的形函數，本文算例采用線性插值函數。

利用式(6)和式(7)，反問題由函數估計問題轉化為參數估計問題。為了構建導熱反問題的目標函數，先把未知參量表示為向量形式

式中:pi表示內壁面選定點處的溫度;N 為選定待反演未知參量的總數。

構建反問題目標函數

式中:T(Pm)為未知向量P 時計算導熱正問題得到的在測量點處的溫度值;Zm為測量溫度值;m = 1，2，…，M，M 為測點總數。

式(9)可寫為

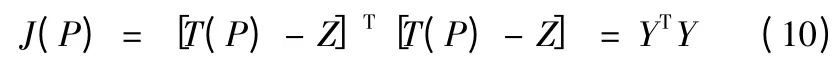
式中:Y 為測量點計算溫度值與測量溫度值的向量差，且Ym=Tm-Zm。由此，導熱反問題即可視為一個優化問題，即利用一定的反演算法，構造出內壁邊界條件，以使目標函數J(P)達到最小。

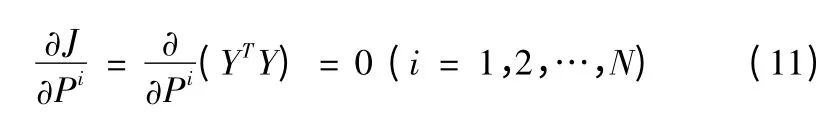
對Y(P)進行Tayor 展開，并省去二階以上高階項，代人式(11)并整理成迭代式得

式中:R 為Jacobian 矩陣。

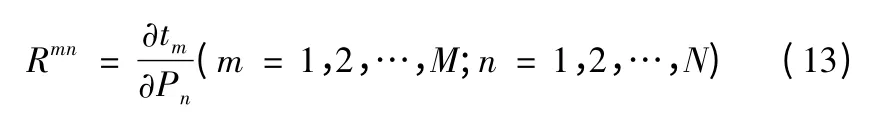
引入修正系數a 調節收斂速度，得Levenberg-Marquar 算法迭代式

式中，I 為(n+1)階單位矩陣。

通過不斷地計算正問題，由式(14)求得新的反演參量，直到未知參量值P 滿足迭代終止條件式(16)

式中:ε 為較小的正數，如1 ×10-6。

3 試驗驗證

針對前面提出的問題，以直角坐標系為例，通過計算鋼-耐火纖維-鋼三層材料組成結構的外表面溫度、熱流密度來驗證上述數學計算模型的正確性。試件結構及尺寸如圖2所示，試件總厚度為80 mm，外殼是厚度為15 mm 的不銹鋼元件，內殼不銹鋼元件厚度為15 mm，中間層為隔熱緩沖層，厚度為50 mm。

假設在距外壁面5 mm，10 mm，25 mm 處各布置有一對熱電偶測溫點，分別命名為1#，2#，3#測溫點。為了計算方便，其初始條件假設為室溫25 ℃，已知邊界條件假設為絕熱邊界。通過三角波形熱流變化模擬和驗證導熱反問題在外壁熱流在該變化情況下的反演計算，并考察測溫點位置、數目及時間步長對計算結果誤差的影響。

首先假設真實熱流變化變化曲線如圖2 所示，以圖2 中三角波形熱流作為初始條件，通過計算導熱正問題方程可得到結構內部溫度場，其中外壁面溫度變化曲線如圖3 所示;然后取3 個測溫點所在位置的溫度變化歷程作為反問題計算輸入條件，可以得到反問題計算熱流及外壁面溫度變化曲線如圖4 和圖5。

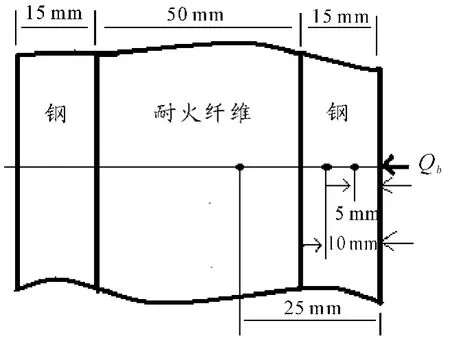
圖2 組合結構和熱電偶分布

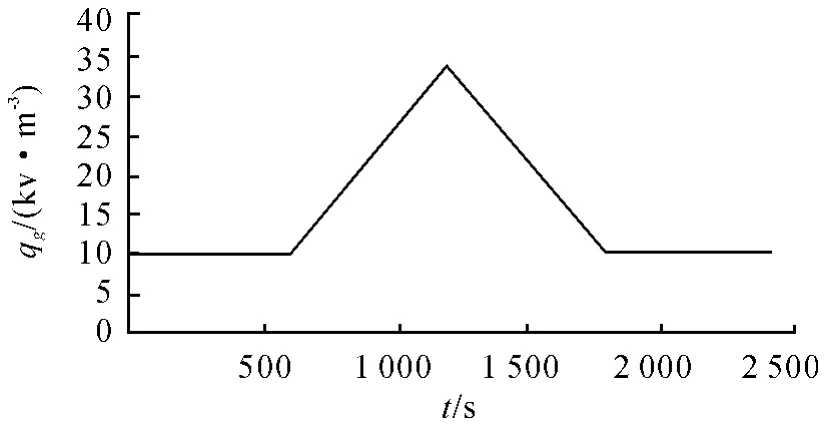
圖3 實際熱流變化曲線

圖4 正問題計算外壁面溫度曲線

圖5 反演熱流變化曲線

從圖2 ～5 可以看出，利用正問題計算得到的內部測溫點溫度值，作為導熱反問題輸入條件的導熱反問題方法，對于三角波形變化熱流(也即緩變熱流)情況下的計算，無論是外壁熱流值還是外壁面溫度值都符合較好。

圖6 反問題計算外壁面溫度曲線

4 結束語

本文所討論的導熱反問題方法，適用于對航天器、火炮身管、核電及化工等大型工程設備進行瞬態傳熱研究時計算介質對容器內壁的放熱系數，該方法不需要布置熱電偶和熱流密度計，而僅需要在容器外壁或內壁布置熱電偶，大大簡化了試驗難度。通過計算模擬鋼-耐火纖維-鋼三層材料組成結構的外表面溫度、熱流密度來驗證上述數學計算模型的正確性。

［1］薛齊文，楊海天.應用共軛梯度法求解非線性多宗量穩態熱傳導反問題［J］.計算力學學報，2005(22):51-54.

［2］陶文銓.傳熱學［M］.西安:西安工業大學出版社，2006:78-103.

［3］吳斌，夏偉，湯勇，等.射擊過程中熱影響及身管熱控制措施綜述［J］.兵工學報，2003，24(4):525-529.

［4］Beck J V，Blackwell B，St C R.clair inverse heat conduction-Ill posed problems［M］. New York: Wiley - Interscience，1985(1):218-243.

［5］Beck J V.Methodology for comparison of inverse heat conduction methods［J］. J. of heat transfer，1988( 110): 30-37.

［6］Lawton B. Thermal-chemical erosion in gun barrels［J］.Wear，2001(251):827-838.

［7］楊冬，陳聽寬.導熱反問題方法在瞬態傳熱過程中的應用［J］.核動力工程，1997，18(6):553-558.

［8］李明海.鋼-木組合結構的火燒熱響應模擬與導熱反問題在火燒試驗中的應用［D］.重慶:重慶大學，1998:42-60.

［9］薛齊文，楊海天.應用共軛梯度法求解非線性多宗量穩態熱傳導反問題［J］.計算力學學報，2005(22):51-54.

［10］楊海天，薛齊文.兩級敏度分析求解非線性穩態多宗量熱傳導反問題［J］. 工程熱物理學報，2003，24(3):463-465.

［11］王靖君，赫信鵬. 火炮概論［M］. 北京: 兵器工業出版社，1997.

［12］趙金輝，何忠波，傅建平，等.火炮發射過程中身管溫度場及彎曲度的有限元計算［J］. 火力與指揮控制，2011(5):106-109.