基于非線性耦合法的張力腿平臺動力特性分析

潘陽，楊樹耕

（天津大學建筑工程學院，天津 300072）＊

張力腿平臺是一種垂直系泊的順應式深水浮式平臺，在深海石油開采中得到了廣泛應用。張力腿平臺作業環境惡劣，同時受到風、波浪、海流等多種環境載荷的作用。對于深水張力腿平臺，隨著水深的增加，錨泊系統和立管系統重力也相應增加，其所受波流載荷、粘性阻尼、非線性錨泊和立管回復力等對系統運動響應的影響也越來越顯著。因此對平臺的運動性能和安全性進行評估時，考慮浮體、錨泊系統和立管系統相互影響的全耦合分析方法是必要的。

波浪載荷作為環境載荷的主要形式之一，是影響深水張力腿平臺安全性的重要因素。張力腿平臺在波浪作用下的運動響應分為波頻響應（WF）、低頻響應（LF）和高頻響應（HF）。波頻響應是由一階波浪力所引起的結構運動響應，幅值較大，是產生波浪載荷的主要形式。由于海浪是含有多種頻率成分的隨機波浪，不同頻率的波浪疊加會產生差頻力與和頻震蕩力，這也正是浮式結構低頻響應和高頻響應的來源。二階波浪力幅值相對一階波浪力較小，但是考慮低頻作用，結構可能產生明顯的定常漂移和周期慢漂運動，高頻波浪會導致明顯的彈振運動（springing）［1］。

文中借助耦合時域分析法，對設計的延伸式張力腿平臺運動性能進行了評估，并在此基礎上，結合二階傳遞函數法［2］（QTF法），計算了準確的二階波浪力的大小，得到了低頻波浪和高頻波浪作用對張力腿平臺的影響，并與Newman近似法［3］得到的結果進行了比較。

1 主要計算理論

1.1 浮體時域計算理論

根據傅里葉變換和卷積積分的方法，時域下的運動方程［4］可寫為

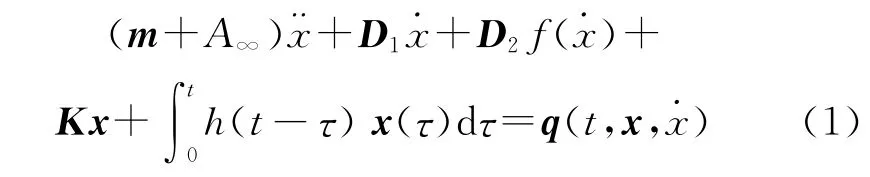
式中：m為結構質量矩陣；D1為線性阻尼矩陣；D2為二階阻尼矩陣；K為回復力剛度矩陣；x為位置矢量；q為激勵力矢量；A∞＝A（ω＝∞），A為與頻率相關的附加質量。

h（τ）為遲滯函數，可通過與頻率相關的附加質量和阻尼變換得到，即

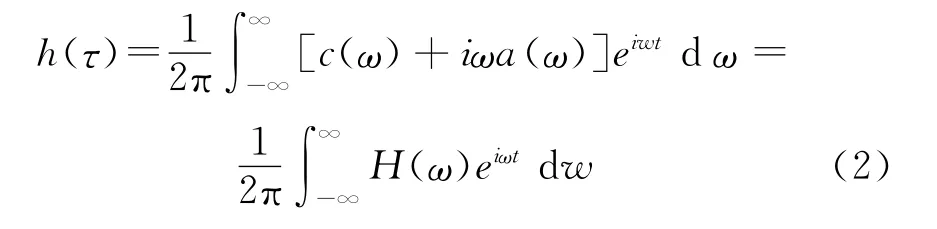
1.2 完整的QTF法及Newman近似法

作用于大尺度結構物上的波浪力的計算［5］以輻射和繞射理論［6］為基礎，其中線性波浪傳遞函數（RAO）的計算考慮了自由表面的線性化的近似，二階波浪力的計算則采用完整的二階傳遞函數法（QTF法），建立了自由表面模型（free surface model），考慮了自由液面上流體質點速度的非線性特點，得到二階傳遞函數QTF（quadratic transfer function），進一步在時域中求解得到二階波浪力的大小。

二階波浪力的一般表達式為

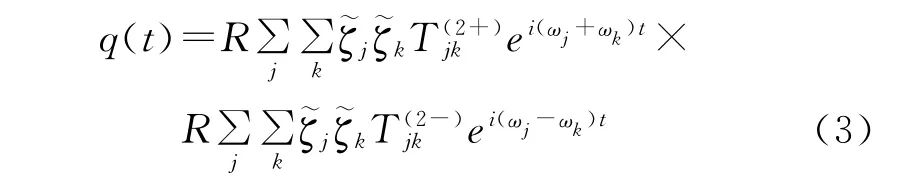
QTF 法是在上式基礎上直接求解波浪力的二階傳遞函數，進一步求解平臺的二階波浪力和運動響應，具有較高的準確性，但計算量大，耗費時間長。當忽略和頻波浪的影響，應用Newman（1974）的定義，即

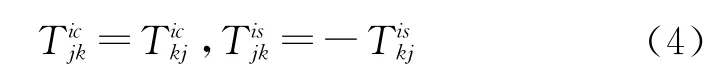
Newman（1974）提出對上式各項進行近似，這樣可大幅度減少計算時間，無需計算二級速度勢。Newman近似的內容可寫為

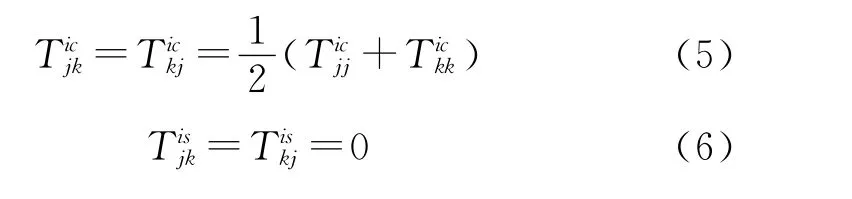
2 延伸式張力腿平臺和模型

2.1 設計平臺主要數據

本文設計的平臺為延伸式張力腿平臺，主要分為3部分：船體及上部結構（TLP）、張力腿系統、立管系統。其中每個懸臂梁各有2根筋腱，水上井口連接有8根生產立管，1根鉆井立管。平臺排水量48327.7t，總質量30510.2t。主要參數如表1，錨泊系統和立管系統如表2。

表1 平臺主體參數 m

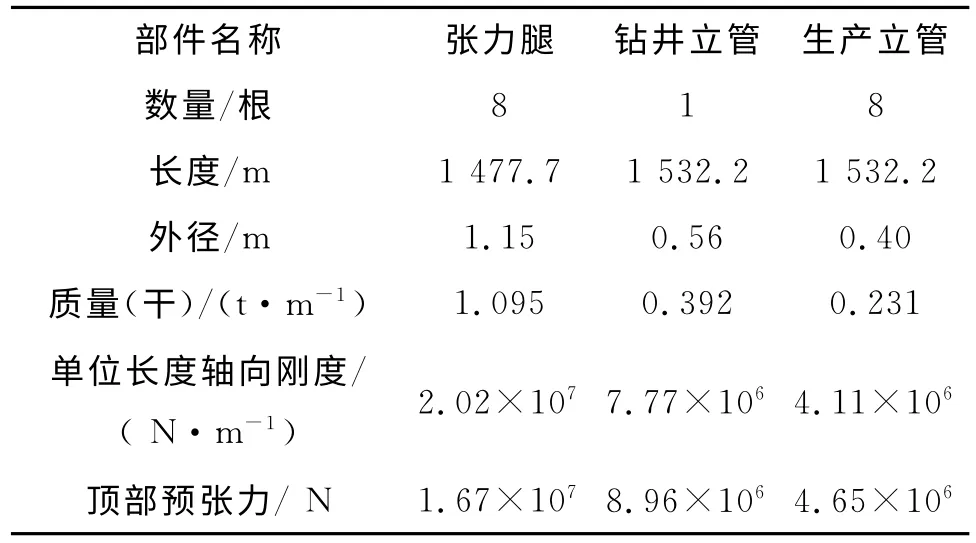
表2 張力腿及立管參數

2.2 載荷條件和計算模型

文中采用SESAM 軟件建模計算，選取適用于南海波浪條件的改進的P－M 波浪譜模擬波浪條件。計算模型主要包括Structrual Model、Hydro Model和Vessel Riser Coupled Model，其中Hydro Model包括Panel Model、Morison Model、Mass Model、Free Surface Model，用以計算一階和二階傳遞函數。圖1為水動力模型，圖2為結構模型。

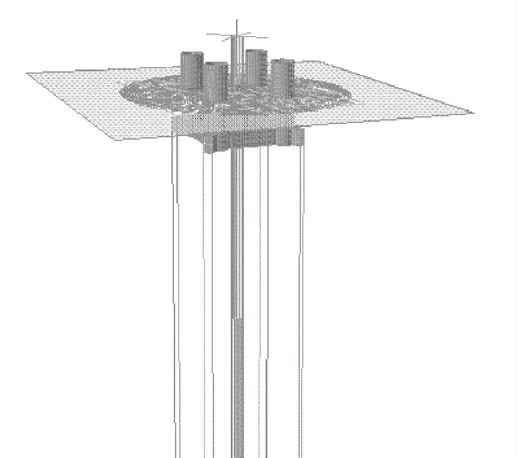
圖1 水動力模型

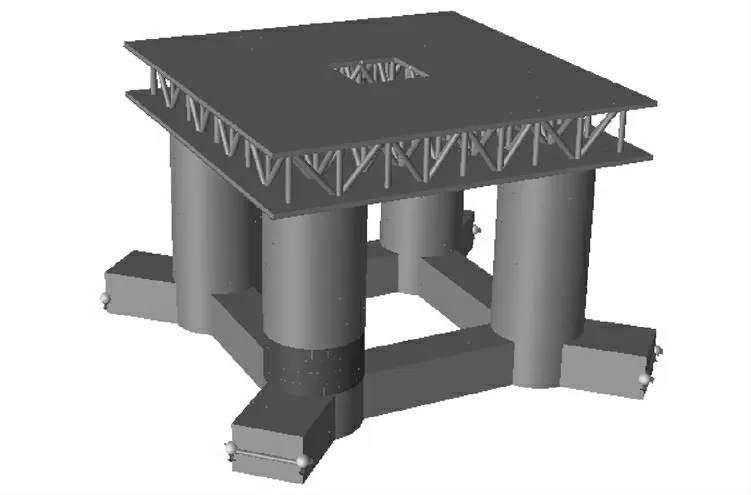
圖2 結構模型

3 一階動力響應分析

綜合考慮風、浪、流的作用，分別計算張力腿平臺在作業工況下和極端工況下平臺的動力響應。表3為2種工況的環境條件［7］。

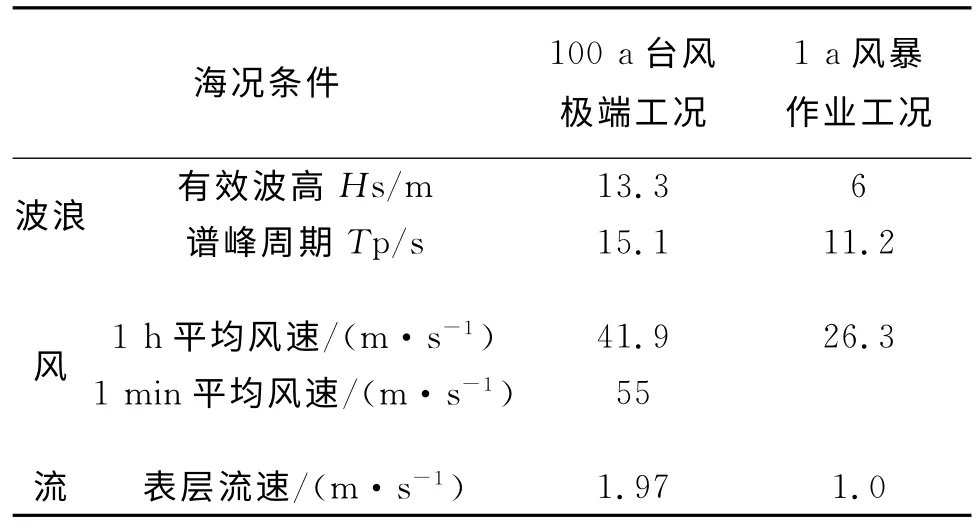
表3 環境條件

表4為2種工況下平臺的動力響應。

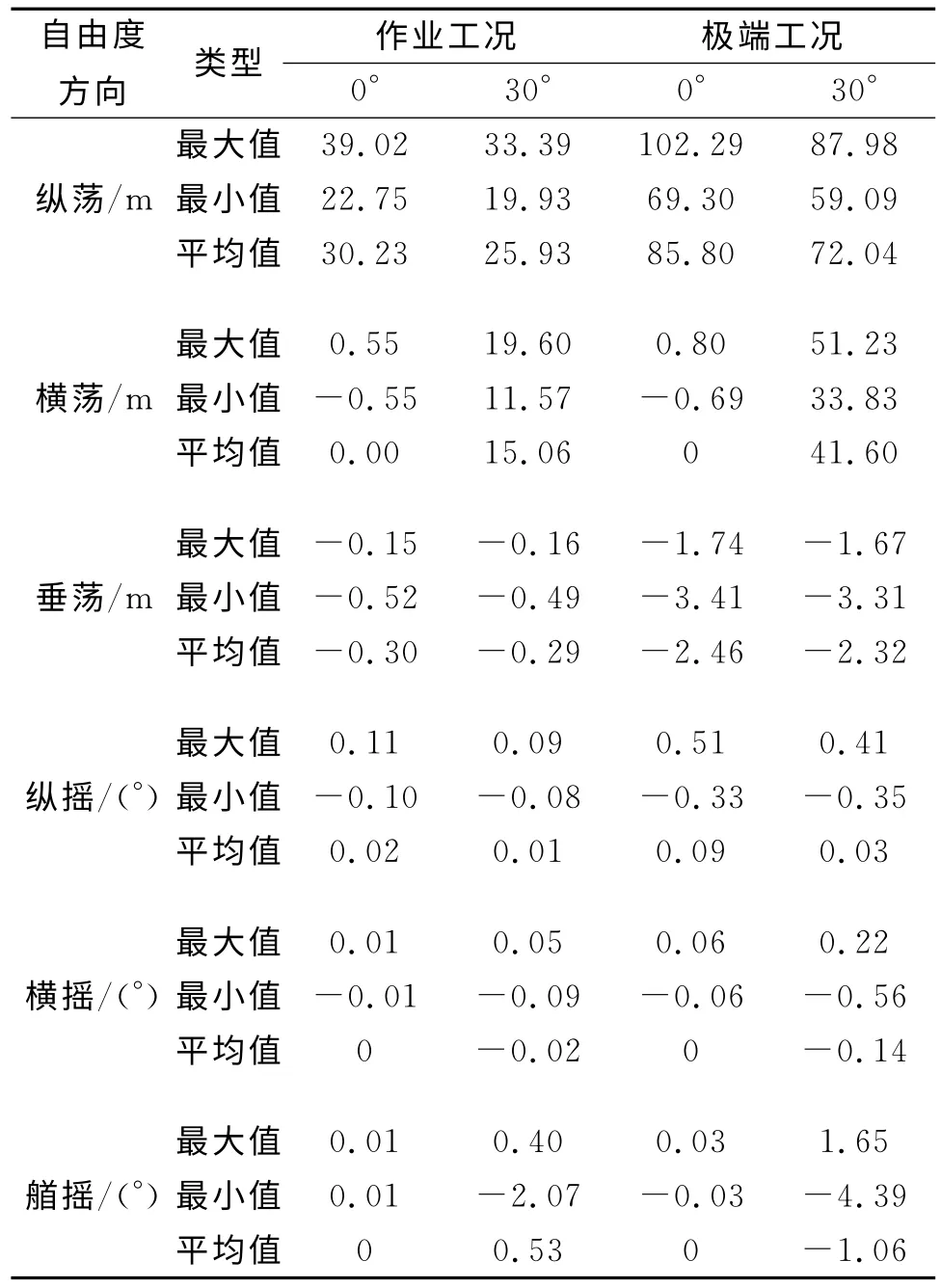
表4 一階平臺運動響應

由運動響應可得：作業工況下，當波流入射角為0°時，TLP的水平運動幅值最大，為39.02 m，約為工作水深的2%～3%，小于水深的5%，同時平臺垂蕩＜±1m，搖擺＜±3°，滿足鉆井作業對平臺運動性能的要求；自存工況下，當入射角為0°時，平臺的水平運動幅值最大，為102.3m，約為水深的7%，小于工作水深的10%，滿足極端工況下一般浮式深水平臺的運動性能要求。

4 基于QTF法的二階波浪力研究

為得到準確的二階波浪力計算結果及對平臺的影響，采用完全QTF 法，選取有效波高13.3m，譜峰周期15.5s，海流表層流速1.2m／s，波流入射角為0°進行計算。水平波浪力計算結果如表5。

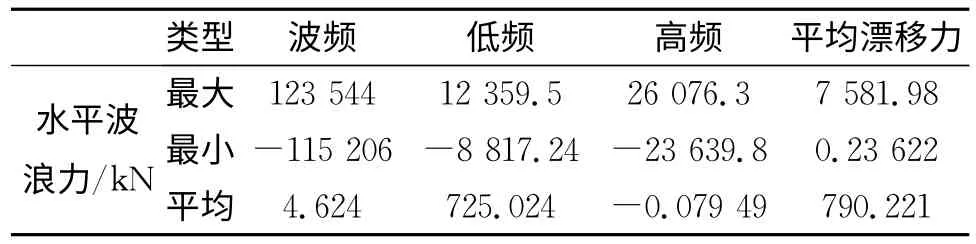
表5 水平波浪力計算結果

由上述計算結果可知：在該結構形式和波譜條件下，二階波浪力、平均漂移力峰值為一階波浪力的1／10～1／5，在TLP設計中不可忽略。圖3～4分別為一階水平波浪力和高頻水平波浪力絕對值的概率分布。

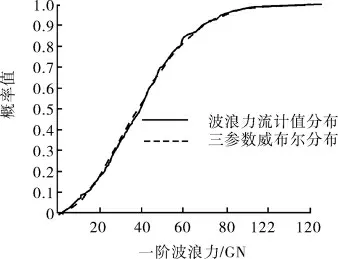
圖3 一階波浪力概率分布

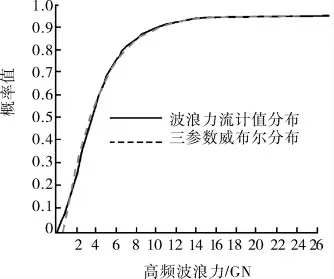
圖4 高頻波浪力概率分布

由波浪力概率分布圖可得：高頻波浪力概率分布曲線明顯較陡，波浪力集中分布在峰值的40%以下，這部分概率達到0.95；一階波浪力分布則相對較為平均，同等比例下的概率只有0.7。

取3500～6500s時段內一階波浪力和二階波浪力統計值，對其數據處理可發現：一階波浪力的大小平均為高頻波浪力的50倍，但在某些時刻，二階波浪力與一階波浪力的值大小相當甚至更大。例如，t＝3689.5s時，波頻波浪力為－5570.4kN，高頻波浪力－11195.8kN。平臺主要運動自由度下的運動響應如表6。

由考慮低頻波浪作用的平臺縱蕩計算結果可知：由于低頻波浪頻率與結構縱蕩固有頻率接近，結構產生了較大的水平漂移，漂移距離可達十幾米，低頻波浪作用的影響十分明顯。

選取xy 正向的其中1根張力腿錨鏈和生產立管，提取其頂端節點處所受拉力，分析二階波浪力對延伸式張力腿平臺錨泊系統和立管系統的影響。

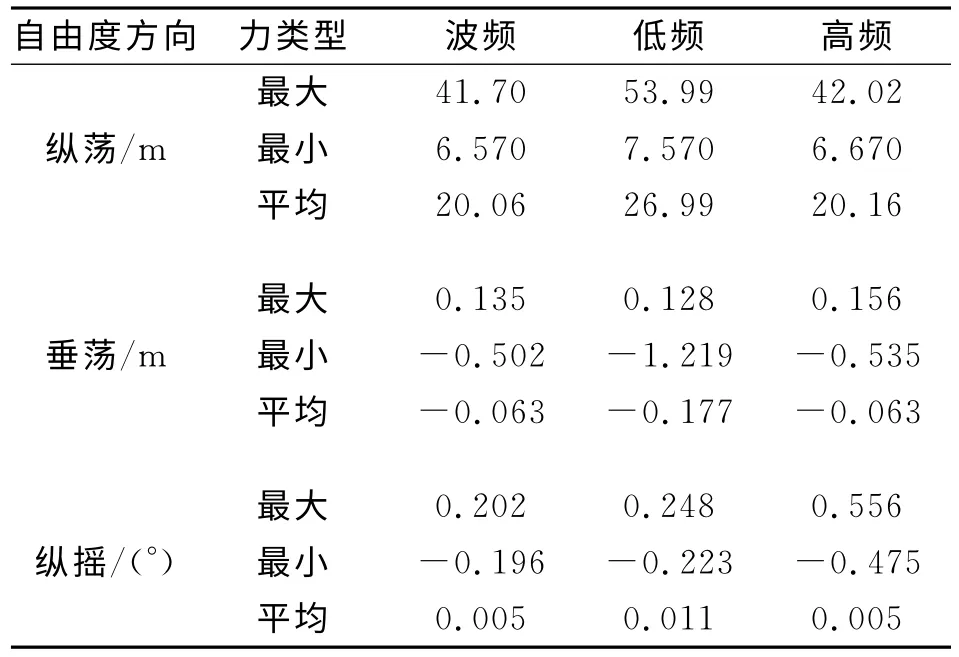
表6 張力腿平臺運動響應

張力腿和立管張力統計值如表7，圖5為只考慮波頻和同時考慮波頻、高頻波浪作用張力腿的張力時程曲線對比。

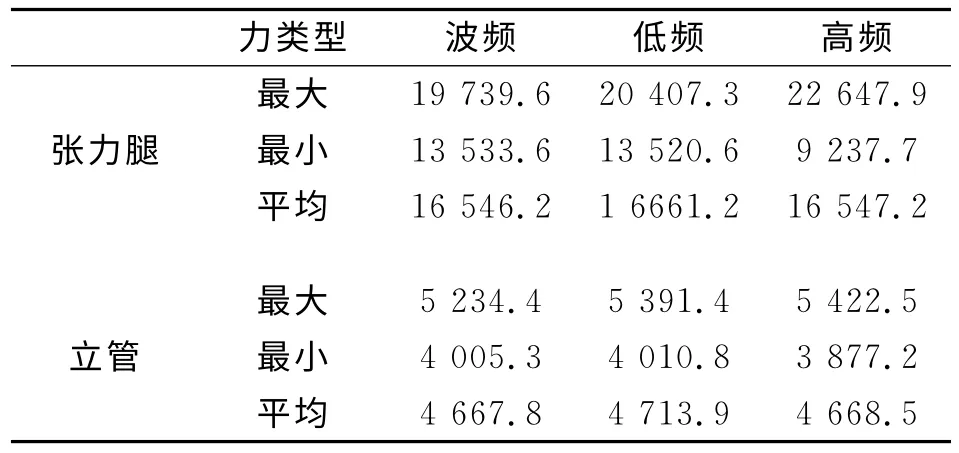
表7 張力腿和立管張力值 kN

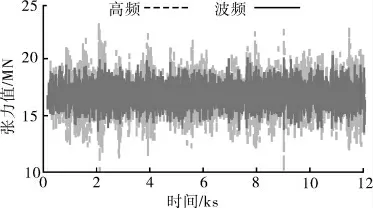
圖5 波頻和高頻波浪作用下張力曲線

由表7和圖5可得：張力腿錨鏈在高頻波浪的作用下，動張力變化幅度顯著增大，為波頻作用下拉力變化幅度的2倍以上，且高頻作用下動張力變化十分劇烈。例如8000s左右時，拉力由20000kN急劇降低為9300kN，這對系索的極限承載力和疲勞壽命的計算有重要影響。生產立管剛度相對較小，承擔的張力較小，因此立管的動張力的變化不明顯。

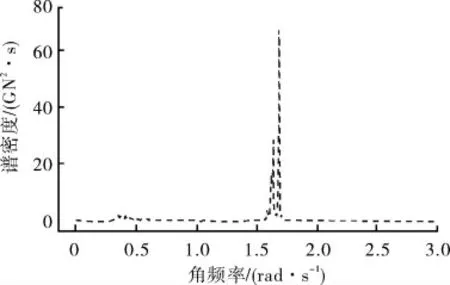
圖6 高頻波浪作用下張力計算譜

5 Newman近似法和QTF法結果比較

QTF法通過求解二階速度勢，得到完整的二階傳遞函數（quadratic transfer function），進一步求解二階波浪力，是二階波浪力的精確解法；Newman近似法忽略了波浪中和頻的成分，根據平均漂移力，對低頻波浪力作了簡化計算，大幅減小了計算量和計算時間。

以自存工況0°入射為例，對2種計算方法結果進行比較，2種方法的得到的縱蕩響應如表8。由表8可得：2種方法得到的縱蕩響應的峰值和平均值誤差不超過1%，QTF 法得到的縱蕩值波動相對較大。

事實上，根據表5，由二階傳遞函數得到的低頻波浪力最大值為12359.5kN，最小值為－8817.2 kN，平均值為725.2kN；Newman近似法得到的二階力雖然峰值偏小，變化幅度較小，平均值為790.2 kN，與QTF法相比誤差僅為10%。因此，在深水平臺的波浪二階力計算中，采用Newman近似的方法來模擬低頻慢漂力作用，具有較高的精度。

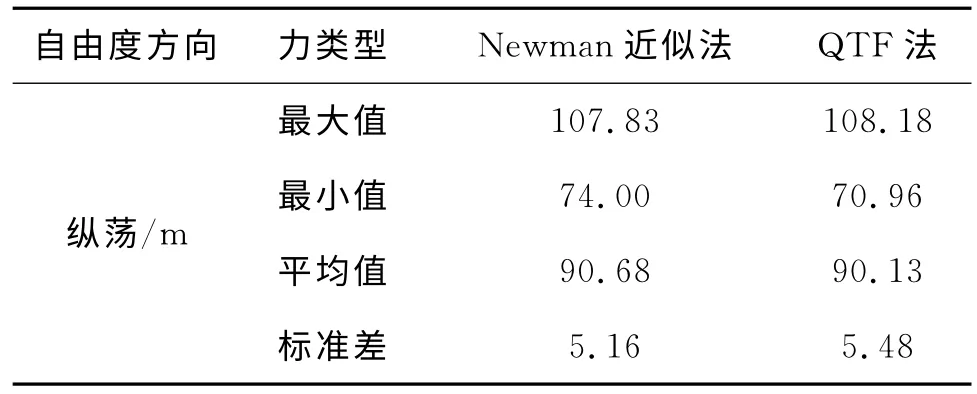
表8 Newman法和QTF法縱蕩響應比較

但是，由于Newman近似法忽略了和頻項，不能反映高頻波浪的影響，因此在實際計算中，為減少計算量，節省計算時間，可以采用Newman近似法和QTF法相結合的方法。

6 結論

1）作業工況下，TLP的最大運動幅值約為工作水深的2%～3%，小于水深的5%，平臺垂蕩＜±1m，搖擺＜±3°；自存工況下，平臺的最大運動幅值約為水深的7%，小于工作水深的10%。該平臺運動幅值在許可的范圍內，有較好的運動性能。

2）二階波浪力的幅值可達到一階波浪力的1／10～1／5，一階波浪力的大小平均為二階波浪力的50倍；但在某些時刻，二階波浪力與一階波浪力的值大小相當甚至更大。低頻二階波浪力會導致張力腿平臺發生明顯的水平漂移，漂移的最大距離超過十幾米。高頻二階力作用會引起張力腿錨鏈所受最大張力顯著增加，并產生劇烈的動張力，變化幅度甚至可達到靜力平衡時錨鏈張力的2／3。

3）對于深水張力腿平臺，Newman近似法在計算低頻平臺響應時，有較高的準確性，誤差＜1%。

［1］董艷秋.深海采油平臺波浪載荷及響應［M］.天津：天津大學出版社，2005.

［2］Lee C H，Newman J N，Kim M H，et al.The computation of second－order wave loads［J］.OMAE’91conference proceedings，Stavanger，Norway，1991：299－302.

［3］楊建民，譯.海洋工程環境載荷［M］.上海：上海交通大學出版社，2006.

［4］Harald O，Elizabeth P.Riflex User Manual［M］.Sesam Users Manual，2008：45－46.

［5］Newman J N.Marine Hydrodynamics［M］.The MIT Press，1997.

［6］Det Norske Veritas.Wave analysis by diffraction and morison theory（Wadam）［M］.Sesam Users Manual，2005：165－168.

［7］陳孝建，劉玉卿，楊樹耕，等，特征參數對延伸式張力腿平臺運動性能影響［J］.石油礦場機械，2012，41（4）：21－24.