（2+1）維Boiti-Leon-Pempinelli方程的精確解

趙艷麗

（成都理工大學工程技術學院 基礎部，四川 樂山 614000）

（2+1）維Boiti-Leon-Pempinelli方程的精確解

趙艷麗

（成都理工大學工程技術學院 基礎部，四川 樂山 614000）

介紹了求解非線性偏微分方程的方法—(G′/G)-展開法。通過使用該方法，并借助Maple得到了（2+1）維Boiti-Leon-Pempinelli（簡稱BLP）方程的多種新精確解，其中包括雙曲函數解、三角函數解和有理函數解等。

（2+1）維BLP方程；(G′/G)-展開法；扭結孤子解；符號計算

尋找非線性偏微分方程的精確解是研究非線性偏微分方程的非常重要的問題，因為物理領域中的許多現象都可以用非線性偏微分方程來描述。近年來，人們一直在想辦法通過直接探討非線性偏微分方程的準確解的結構來得到它的精確解，已獲得了許多求解非線性方程的準確解的方法，例如：雙曲正切函數展開法［1-3］、正弦-余弦法［2-3］、指數函數法［3-4］、Hirota's雙線性法［5］、Jaco?bi橢圓函數展開法［6］、修改的tanh展開法［7］、輔助微分方程［8-10］等，文獻［11］提出了(G′/G)-展開法，本文將利用這一方法構造BLP方程的精確解。

1 (G′/G)-展開法

首先，利用一個行波變換 ξ=α(x+y+ct)將非線性偏微分方程

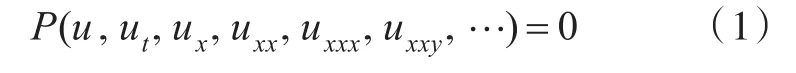
變成常微分方程

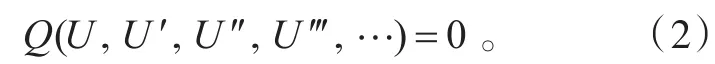
下一步，把未知量U展開為含有(G′/G)的冪級數

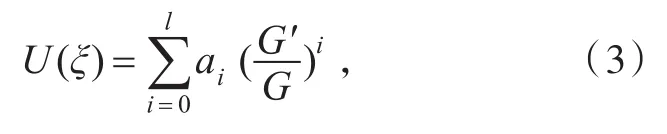
其中αi(i=0，1，2，…，l)是待定常數，正整數l由平衡方程（2）的最高階導數項和最高階非線性項來決定，G滿足

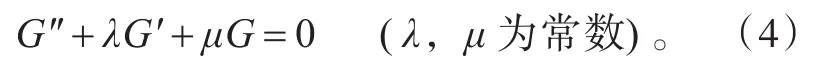
由方程（4）的解，我們可以得到關于(G′/G)的下列結果：

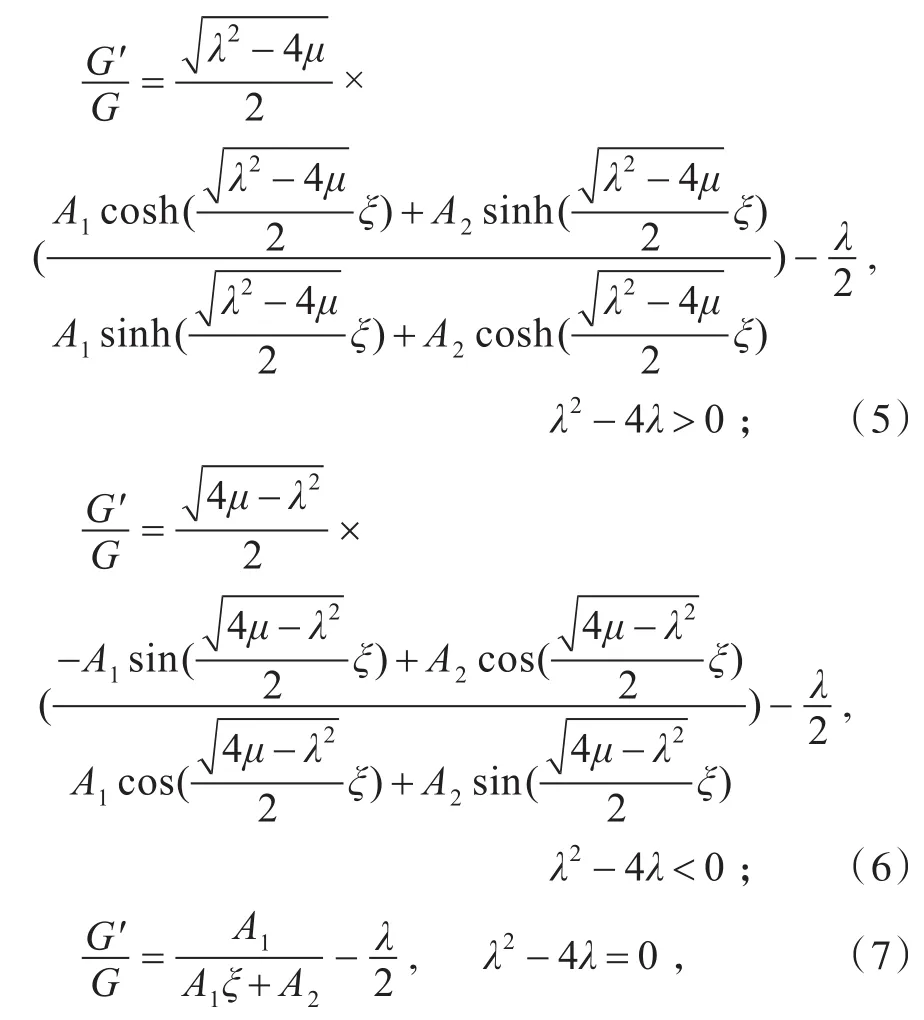
其中 A1，A2為任意實數。把方程（3）、（4）代入方程（2），可以得到一組關于(G′/G)的代數方程。合并(G′/G)的同冪次項，令同冪次項的系數為零，可以得到一組關于αi(i=0，1，2，…，l)，α，c的代數方程。借助Maple求解這個代數方程組，得到方程組（2）的精確解。

2 （2+1）維BLP方程的精確解

近年來，數理學家對(2+1)維BLP方程

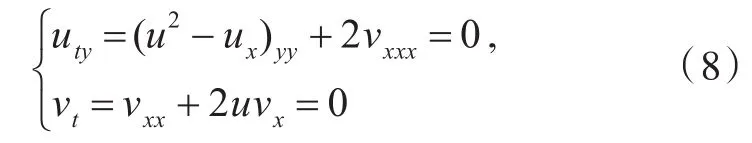
做了很多研究［12-15］。文獻［12-13］采用雙曲正切方法，文獻［14］采用廣義代數方法，文獻［15］采用改進的Riccati方程方法，分別得到了方程組（8）的扭結孤子解和行波解。

為了尋找方程組（8）的精確解，引入行波變換ξ=α(x+y-ct)，將方程組（8）轉變為常微分方程組

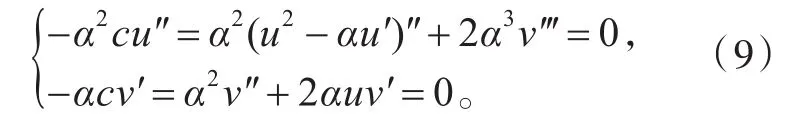
對方程組（9）的第一個方程積分兩次，忽略積分常數，得

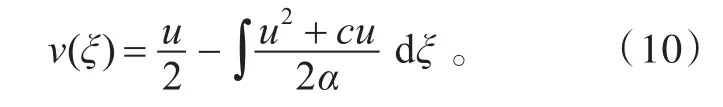
把方程（10）代入方程組（9）的第二個方程中，得到一個非線性的常微分方程

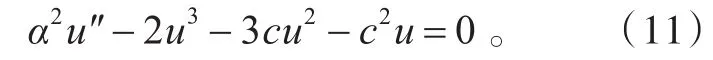
利用方程（3）和方程（4），在方程（11）中，平衡φ″和φ3，得l=1。因此，

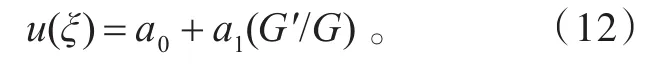
將（12）式代入（11）式，令所有(G′/G)的同冪次的系數等于零，得到下列關于a0，a1，α，c的代數方程

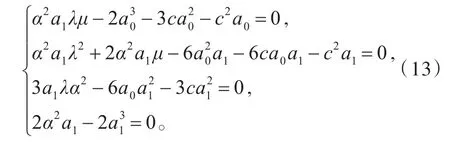
借助Maple，求解方程組（13），得到下列幾種情形：

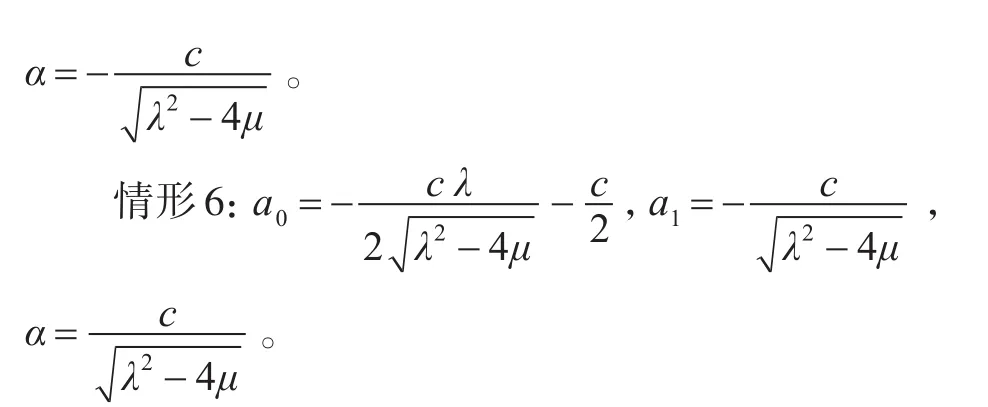
其中c為任意常數。

將上述結果代入方程組（8），利用方程（5）～方程（7），得到方程組（8）的下列精確解。

利用情形1，有

（a1）：當 λ2-4μ＞0時，方程組（8）有如下形式的雙曲函數解

如果 A1=0，A2≠0，λ＞0，μ=0，由（14），（15）式得u1、v1的另一種形式為

特別地，u1.3是（2+1）維BLP方程的扭結孤子解。

如果 A1≠0，A2=0，λ＞0，μ=0，由（14）、（15）式，u1、v1的另一種形式為

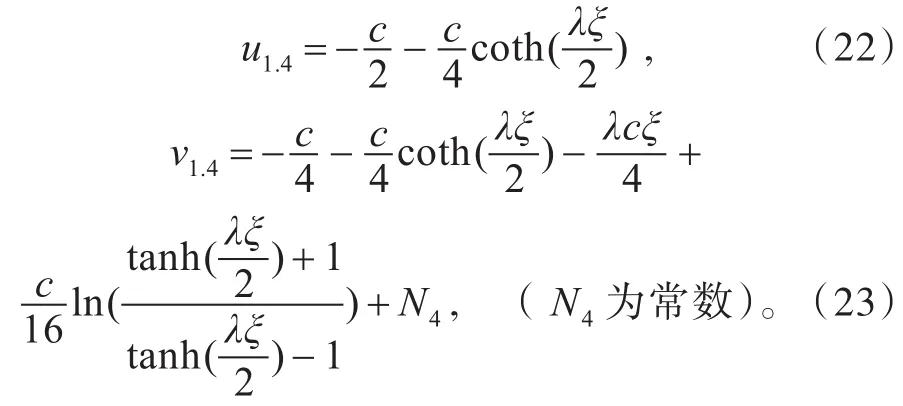
（a2）：當 λ2-4μ＜0時，方程組（8）有如下形式的三角函數解

（a3）：當 λ2-4μ=0時，方程組（8）有如下形式的有理函數行波解

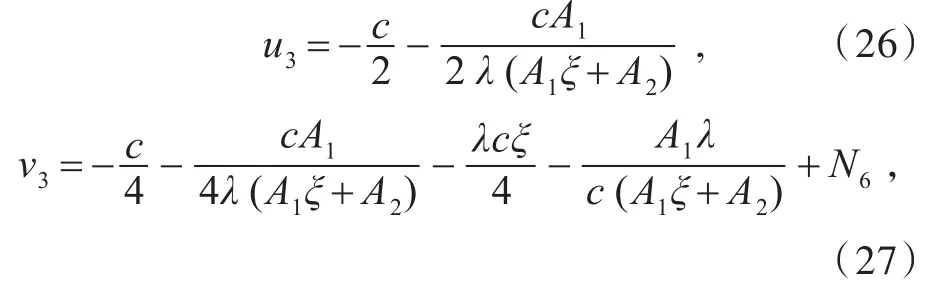
利用情形2～情形6以及方程組（10）和方程組（12）的廣義解，可以得到方程組（8）的更多精確解。簡單起見，這里不再一一論述。

3 結語

筆者采用 (G′/G)-展開法獲得了（2+1）維BLP方程的精確解，這些解包括雙曲函數解、三角函數解和有理函數解等。其中的一些結果在不同的系數條件下可以轉換為孤子形式，而且對比文獻［10-13］，本文的結果更為豐富。

［1］ 范恩貴.可積系統與計算機代數［M］.北京：科學出版社，2004.

［2］ 閆振亞.復雜非線性波的構造性理論及其應用［M］.北京：科學出版社，2007.

［3］ Moghaddam M Y，Asgari A，Yazdani H.Exact travellingwave solutions for the generalized nonlinear Schr?inger（GNLS） equation with a source by Extended tanh-coth，sine-cosine and Exp-Function methods［J］. Applied Mathematics and Computation，2009，210（2）：422-435.

［4］ Khanib F，Hamedi-Nezhadc S，Darvishia M T，et al. New solitary wave and periodic solutions of the foam drainage equation using the Exp-function method［J］. Nonlinear Analysis：Real World Applications，2009，10（3）：1904-1911.

［5］ Xu X G，Meng X H，Gao Y T，et al.Analytic N-soli?tary-wave solution of a variable-coefficient Gardner equation from fluid dynamics and plasma physics［J］. Applied Mathematics and Computation，2009，210（2）：313-320.

［6］ 劉式適，傅遵濤，劉式達，等.Jacobi橢圓函數展開法及其在求解非線性波動方程中的應用［J］.物理學報，2001，50（11）：2068-2073.

［7］ El-Wakil S A，Abdou M A.Modified extended tanhfunction method for solving nonlinear partial differential equations［J］.Chaos，Solitons and Fractals，2007，31（5）：1256-1264.

［8］ Chen Y，Wang Q.A series of new soliton-like solutions and double-likeperiodic solutions of a（2+1）-dimen?sional dispersive long wave equation［J］.Chaos，Soli?tons and Fractals，2005，23（3）：801-807.

［9］ Elgarayhi A.New solitons and periodic wave solutions for the dispersive long wave equations［J］.Physica A，2006，361（2）：416-428.

［10］Sun Y H，Ma Z M，Li Y.Explicit solutions for general?ized（2+1）-dimensional nonlinear zakharov-kuznetsov equation［J］.Commun Theor Phys，2010，54（3）：397-400.

［11］Wang M L，Li X Z，Zhang J L.The（G’/G）-expansion method and travelling wave solutions of nonlinear evolu?tion equations in mathematical physics［J］.Physics Let?ters A，2008，372（4）：417-423.

［12］Feng W G，Li K M，Li Y Z，et al.Explicit exact solu?tions for（2+1）-dimensionnal Boiti-Leon-Pempinelli equation［J］.Commun Nonlinear Sci Numer Simulat，2009，14（5）：2013-2017.

［13］Lü Z S，Zhang H Q.Soliton like and multi-soliton like solutions for the Boiti-Leon-Pempinelli equation［J］. Chaos，Solitons and Fractals，2004，19（3）：527-531.

［14］Ren Y J，Liu S T，Zhang H Q.A new generalized alge?bra method and its application in the（2+1）dimen?sional Boiti-Leon-Pempinelli equation［J］.Chaos，Soli?tons and Fractals，2007，32（5）：1655-1665.

［15］Huang D J，Zhang H Q.Exact travelling wave solutions for the Boiti-Leon-Pempinelli equation［J］.Chaos，Soli?tons and Fractals，2004，22（1）：243-247.

Exact Solution of（2+1）-dimensional Boiti-Leon-Pempinelli Equation

ZHAO Yan-li
（Foundations Department，Engineering and Technical College，Chengdu University of Technology，Leshan 614000，Sichuan，China）

The(G′/G)-expansion method is brief introduced to solve nonlinear partial differen?tial equations.Many exact solutions of the（2+1）-dimensional Boiti-Leon-Pempinelli equation（BLPE）are obtained with this method and with the aid of Maple，these solutions include hyperbolic function solution，trigonometric function solutions and rational function solutions ect.

（2+1）-dimensional Boiti-Leon-Pempinelli equation；(G′/G)-expansion meth?od；kink soliton solution；symbolic computation

O175.23

：A

：1673-0143（2013）01-0019-04

（責任編輯：強士端）

2012－12－02

國家自然科學基金資助項目（11271066）

趙艷麗（1980—），女，助教，碩士，研究方向：偏微分方程。