風速波動下風電場變參數等值建模方法

蘇勛文 徐殿國 卜樹坡

（1.哈爾濱工業大學電氣工程博士后流動站 哈爾濱 150001 2.黑龍江科技學院電氣與信息工程學院 哈爾濱 150027 3.蘇州工業職業技術學院電子與通信工程系 蘇州 215104）

1 引言

隨著風電技術的快速發展以及“陸上三峽”的實施，大型風電場以及風電場群已經形成。在風電場并網系統的仿真分析中，若對每臺風電機組進行詳細建模將極大增加仿真的復雜度，導致計算時間長、資源利用率低。因此風電場等值建模方法的研究已成為當前熱點[1-11]。

國家電網公司于2009年10月頒布了風電場接入電網技術規定實施細則[12]。技術規定中提出了需確保風電場并網點的最大輸出功率及功率變化率不超過電網調度部門給定值，為此需要能準確地反映風速波動下風電場并網點動態特性的等值建模方法，本文主要研究風速波動下定速機組風電場的等值建模方法。

目前，常用的定速機組風電場等值方法為單機表征法[13-19]，即把風電場等值成一臺風力機和一臺發電機，其輸入為平均風速（常用等值方法1）；或保留所有風力機和風速模型，并以疊加的機械轉矩作為等值發電機的輸入（常用等值方法2）。文獻[13]指出：當風電場風速差異較大時，風速波動下利用常用動態等效建模方法得到的風電場等效模型會存在一定的無功功率誤差。為此，文獻[18]針對機端加裝固定電容器的情況給出了一種變參數補償的方法，但其計算公式中含有等值前每臺風電機組的電壓，因此該方法難以實現。關于定速機組風電場的動態等效建模研究一般僅考慮機端按固定電容器補償的情況，而缺少對機端按分組投切電容器補償的風電場動態等效建模方法進行研究。

鑒于此，本文提出一種適合風速波動下定速機組風電場的變參數電容補償等值建模方法。通過誤差原因分析，推導變參數電容的計算方法，分別給出機端兩種無功補償方式的等值處理方法，同時在PSCAD/EMTDC 仿真平臺上建立了風電場變參數模型。通過仿真驗證了方法的有效性。

2 變參數等值建模方法的主要思想

文獻[13]指出了常用等值方法建立的等值模型出現無功功率誤差的原因是：①等值風電機組輸出的無功功率與等值前所有風電機組輸出的無功功率之和并不相等；②等值方法中等值并聯電容器計算方法的前提是假定所有機組的機端電壓相同，但對于大型風電場，每臺風電機組的機端電壓各不相同，因此會造成誤差；③等值方法中沒有考慮風電場內電纜充電電容對風電場出口側無功功率的影響。由于風速是變化的，從而無功功率誤差的大小也是變化的。為此給出一種變參數電容來補償等值前后無功功率的誤差。

變參數等值建模方法是將風電場等值成一臺風電機組，采用機械功率疊加的方法得到等值風電機組的輸入機械功率，并將變參數電容連接到等值風電機組的機端。

該方法需解決的主要問題有：①推導出變參數電容的計算方法；②分別給出機端固定電容器和分組投切電容器兩種無功補償方式的等值模型結構；③在仿真平臺下建立風電場變參數模型。

3 變參數電容計算方法

變參數電容由兩部分組成，它們分別對應無功功率誤差產生的前兩個原因，其表達式為

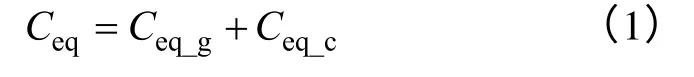
式中，Ceq為變參數電容；Ceq_g為補償風電機組無功誤差的變參數電容；Ceq_c為補償機端電容器無功誤差的變參數電容。

對于第三個誤差原因，由于其充電電容補償是固定值，且不在風電機組機端，因此將在后面考慮。下面分別給出兩種機端無功補償方式變參數電容的詳細描述。

3.1 機端固定電容器補償方式

3.1.1 補償風電機組無功誤差的變參數電容計算

圖1 給出了機端固定電容器補償的定速風電機組模型。

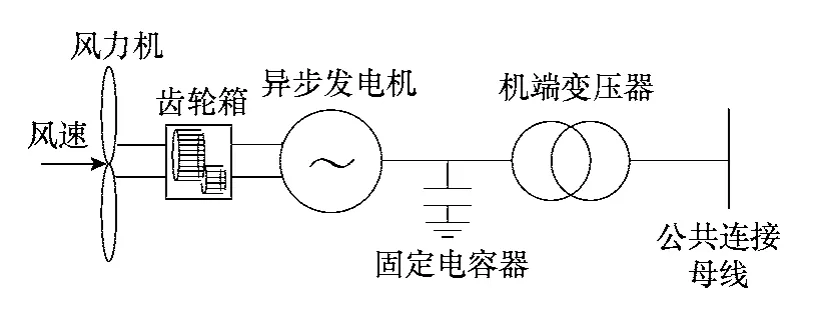
圖1 固定電容器補償的定速風電機組模型Fig.1 Fixed-speed wind turbine of fixed capacitor compensation

由感應電機理論可知，電機的電磁轉矩為[20]

式中，x1、x2分別為發電機定子電抗和轉子電抗；r2為發電機轉子電阻；s為轉差；U為發電機機端電壓。用風電機組的機械功率代替電磁轉矩，經整理可得轉差為

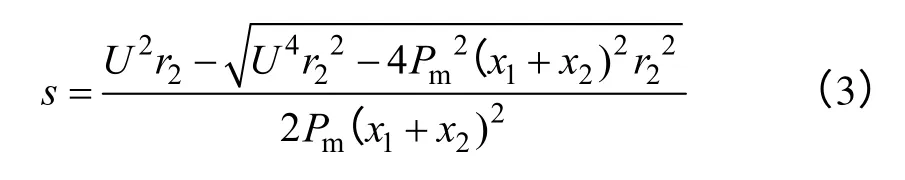
式中，Pm為機械功率。進一步可得定速風電機組吸收的無功功率與有功功率之間的關系為

式中，Qe為無功功率；Pe為有功功率；xm為勵磁電抗；xk為定子和轉子電抗之和。式（4）可簡寫成

式中，f(·)為風電機組吸收的無功功率與有功功率之間的對應函數。等值前所有風電機組吸收的無功功率為

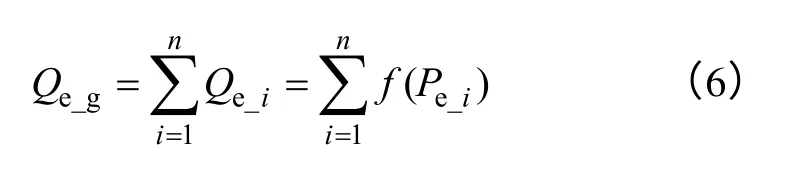
式中，Pe_i為等值前第i臺風電機組的有功功率；Qe_i為等值前第i臺風電機組的無功功率；n為風電場內風電機組的臺數。

等值后等值風電機組吸收的無功功率為

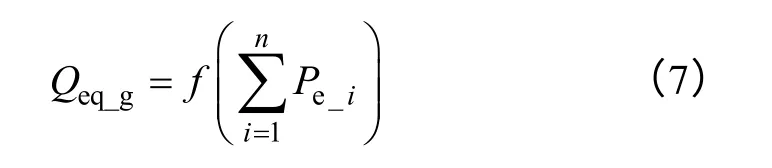
由于等值前后Qeq_g≠Qe_q，所以在等值模型中需要用變參數電容來補償等值前后風電機組的無功功率差值。其計算公式為

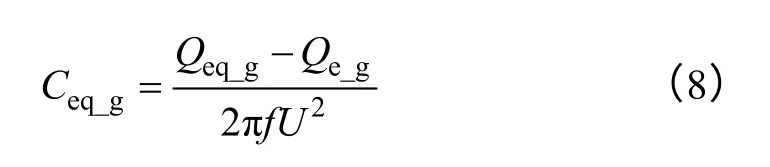
式中，f為頻率；U為等值風電機組機端電壓，應用時電壓標幺值可近似取為1。

根據等值前后固定電容器發出的無功功率相等，可得

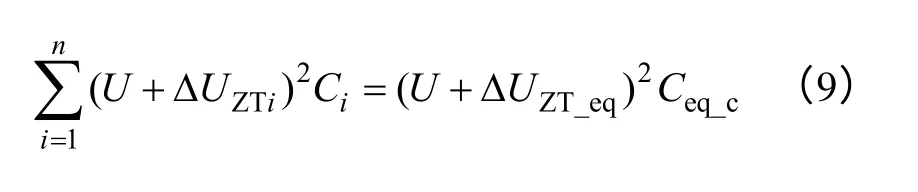
式中，ΔUZTi、Ci分別為等值前第i臺定速風電機組的機端變壓器電壓降落和固定電容器的電容值；ΔUZT_eq為等值定速風電機組的等值變壓器電壓降落。利用歐姆定律變壓器壓降ΔUZTi=IiZTi，等值后變壓器電流為等值前所有風電機組電流之和，則有，代入上式，展開后可得變參 數電容為

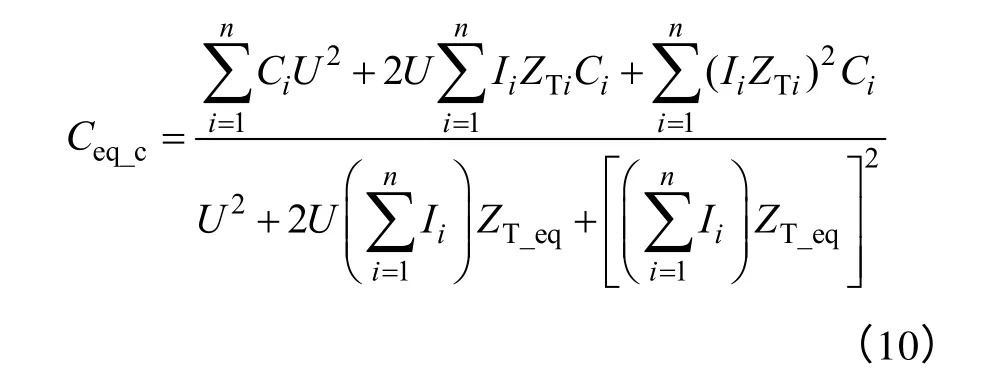
式中，Ii為等值前第i臺定速風電機組的輸出電流；ZTi為等值前第i臺定速風電機組的機端變壓器阻抗；ZT_eq為等值變壓器的阻抗。

風電機組的電流和視在功率存在如下關系

把式（11）代入式（10）中，并假定無功補償裝置使得風機機端功率因數近似等于1，可用風電機組有功功率替代視在功率，得等值電容計算公式為

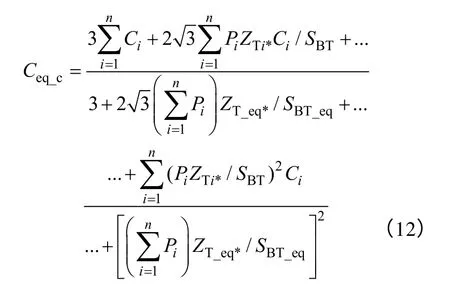
式中，SBT、SBT_eq分別為等值前、后變壓器阻抗的基準容量；ZTi*、ZT_eq*分別為等值前、后變壓器阻抗標么值；Pi為等值前第i臺風電機組的有功功率。

式（12）表明，只需已知等值前風電機組的輸出功率及相關參數，不需要知道等值前每臺風電機組機端電壓，就可方便地計算變參數電容。在實際應用中可通過風速預測以及風電機組的功率曲線得到風電機組的輸出功率，因此上述方法易于實現。

3.2 機端分組投切電容器補償方式

本文采用河北某風電場750kW 風電機組進行分析，該機組機端采用分組投切電容器補償方式，其控制規律見表1。該分組投切電容器分五級，電容器組的投切是根據風電機組的輸出功率進行控制。其結構如圖2 所示。圖2 中S1～S4分別表示第2～5 組電容器的開關。

互聯網金融簡言之是將金融功能以互聯網技術為載體，依托云計算在互聯網平臺形成的金融服務體系。互聯網金融在人們普遍認識和接受互聯網的基礎上，將互聯網與傳統金融結合，形成的滿足目前市場需求的新型金融模式，其本質是金融，媒介是互聯網。互聯網金融發展快、覆蓋率高、效率高、成本低，明顯彌補了傳統金融市場的短板[1]。但是互聯網金融發展時間短，模式尚存在漏洞，如管理弱，風險管控困難，目的不明確等缺點。

表1 分組投切電容器的分組與補償容量Tab.1 Grouping and compensation capacity of grouping switching capacitor

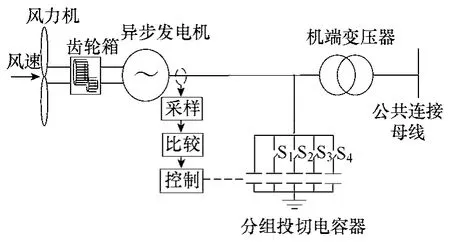
圖2 分組投切電容器補償的定速風電機組模型Fig.2 Fixed-speed wind turbine of grouping switching capacitor compensation

機端按分組投切電容器補償的變參數電容計算方法同機端按固定電容器補償的情況。其中，補償風電機組無功誤差的變參數電容按式（8）計算，補償機端電容器無功誤差的變參數電容計算按式（12）計算，不同點是，式中的Ci需要首先根據分組投切電容器的控制規律得到，再代入式（12）計算。

4 風速波動下風電場等值建模

4.1 等值風電機組的參數計算

設風電場由n臺相同型號的風電機組組成，利用變參數的等值建模方法是將風電場等值成一臺風電機組，采用機械功率疊加的方法得到等值風電機組的輸入機械功率，等值風電機組的各部分參數（有名值）計算公式分別為

（1）等值感應電機參數

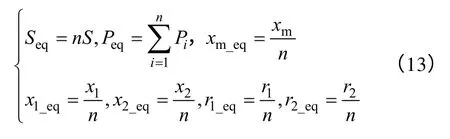
式中，下標eq 表示等值后；S、P分別表示容量、有功功率。

（2）軸系參數

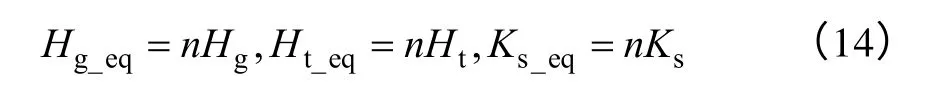
式中，Ht、Hg分別為風力機和發電機的轉子慣性時間常數；Ks為軸系剛度系數。

（3）電容器和變壓器參數

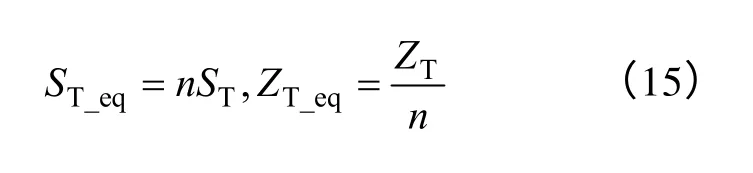
式中，ST為機端變壓器容量；ZT分別表示機端變壓器阻抗。

（4）等值電纜充電電容。對于電纜充電電容的等值處理，可忽略風電場內的電壓差異，等值電纜充電電容等于等值前所有電纜的充電電容之和。

4.2 變參數電容補償的等值步驟

（1）根據式（8）計算補償風電機組無功誤差的變參數電容。

（2）根據式（12）計算補償機端固定電容器的變參數計算，如果機端是分組投切電容器補償的情況，首先根據控制規律計算每臺風電機組的Ci，再代入式（12）中計算變參數電容。

（3）首先將前兩步計算結果相加，得到變參數電容，然后將所有風電機組按機械功率疊加的方法合并成一臺等值風電機組，并把變參數電容接到等值風電機組機端。

（4）計算等值風電機組的其他參數，得出風電場變參數等值模型。

4.3 PSCAD/EMTDC 平臺的變參數風電場模型

在PSCAD/EMTDC 平臺上搭建了變參數風電場等值模型，圖3 給出了機端固定電容器補償方式的風電場變參數等值模型結構，圖4 給出了機端分組投切電容器補償方式的風電場變參數等值模型結構。

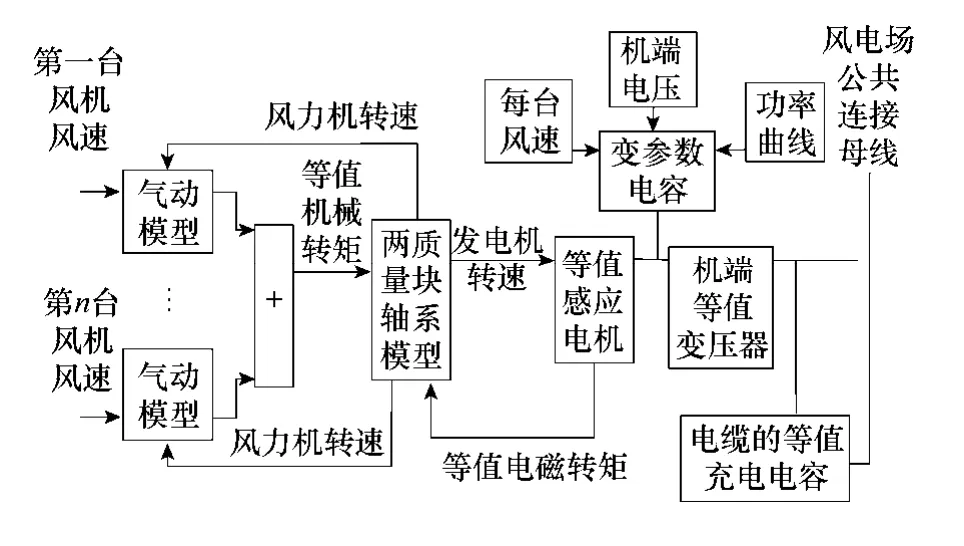
圖3 固定電容器補償的風電場變參數等值模型Fig.3 Wind farm variable parameter equivalent model of fixed capacitor compensation

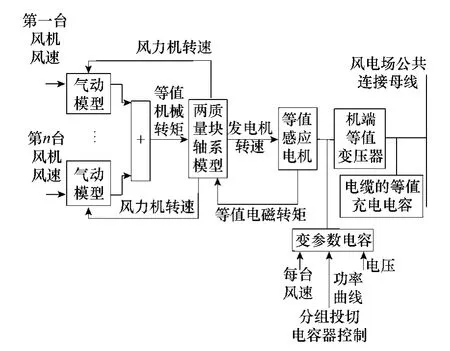
圖4 分組投切電容器補償的風電場變參數等值模型Fig.4 Wind farm variable parameter equivalent model of grouping switching capacitor compensation

4.4 等值模型誤差分析

為了比較不同等值方法的優劣，定義了兩個評價指標，分別是有功相對誤差EP和無功相對誤差EQ，其計算公式為

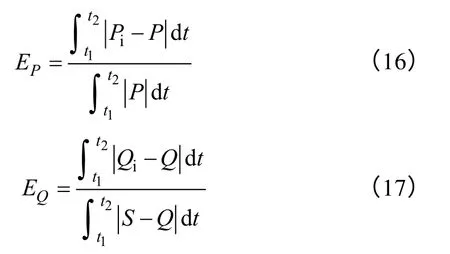
式中，P、Q為風電場詳細模型在風電場出口側的有功功率、無功功率；Pi、Qi為等值方法i的風電場等值模型在風電場出口側的有功功率、無功功率；S為風電場的裝機容量；t1、t2分別為誤差分析的起始和終止時間。

5 算例分析

5.1 測試系統及參數

圖5 是風電場算例的結構示意圖，該風電場由25 臺定速風電機組組成，風電機組經并聯電容器組、機端變壓器（10.5kV/690V）和電纜連接 PCC上，并通過風電場出口變壓器（110kV/10.5kV）和架空線路連接到外部電網。其中，風力機、發電機、變壓器和電纜等主要參數見表2。

5.2 機端按固定電容器補償

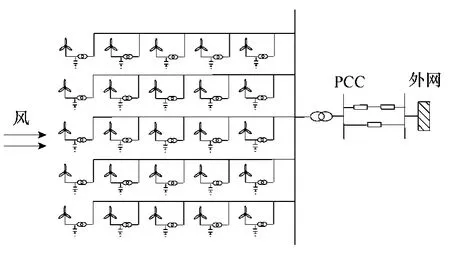
圖5 風電場系統單線示意圖Fig.5 Single line diagram of wind farm

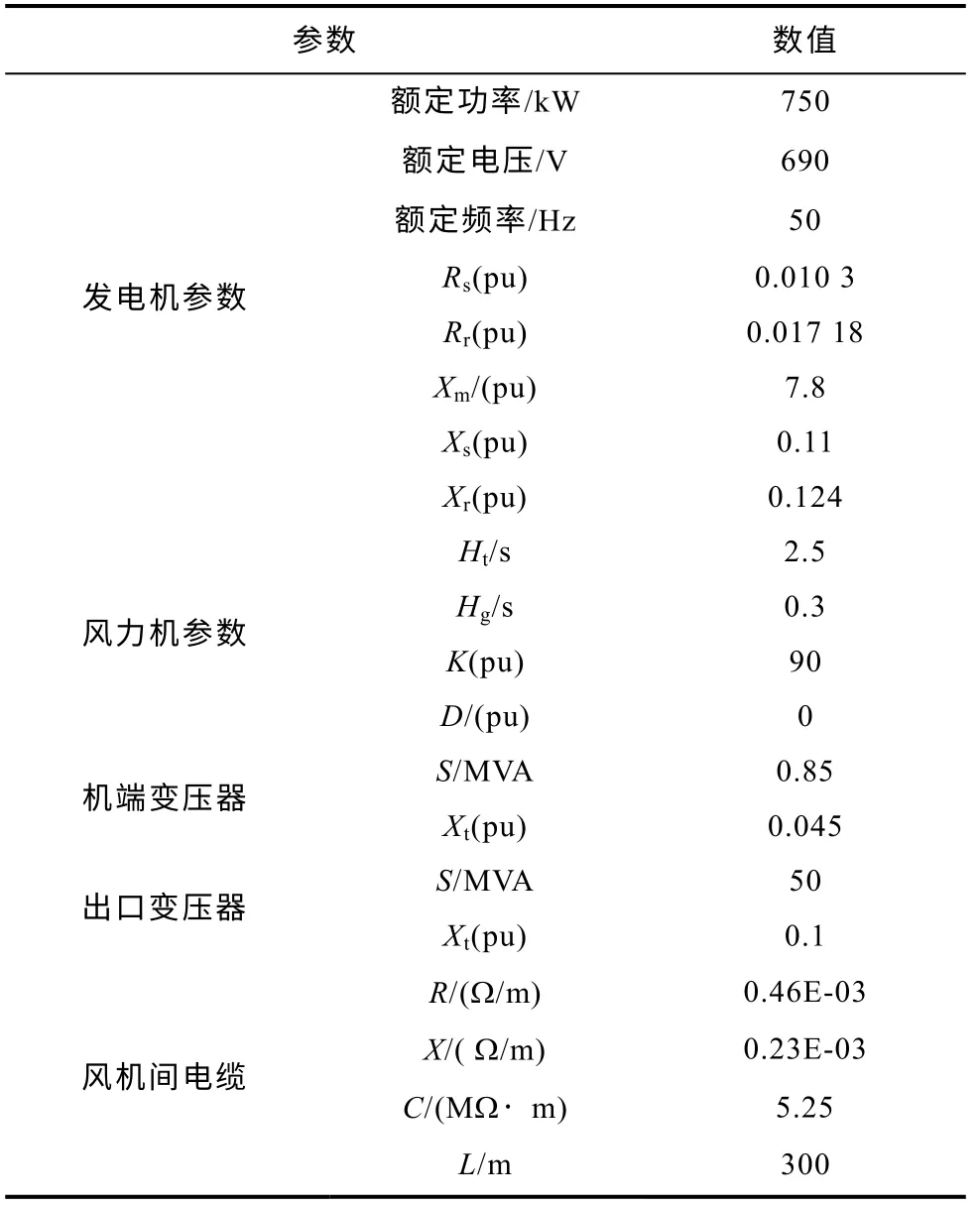
表2 風電場電氣參數Tab.2 Electric parameters of wind farm

機端固定電容器補償按照每臺風電機組1 500μF 補償。由文獻[13]可知，風電場常用等值方法2 優于常用等值方法1，因此本文對常用等值方 法2 和提出的變參數電容補償法進行了比較。圖5中風電場由5 排5 列25 臺風電機組組成，風機間以及風機與PCC 母線的電纜長度均為300m，風由左向右吹過風電場，并考慮尾流效應和時滯的影響。當考慮尾流效應時，假定第二排風速比第一排風速小2m/s，其他排風速比前排風速小1m/s；當考慮時滯時，后排風速相比前排的延遲時間為25s。圖6給出了風電場詳細模型、等值方法2的模型以及變參數電容補償等值方法的模型在并網點A的有功功率、無功功率以及電壓的動態響應過程曲線，同時給出了迎風向第一排風速曲線。并分別根據式（16）、式（17）計算有功功率和無功功率的誤差指標，其結果見表3。

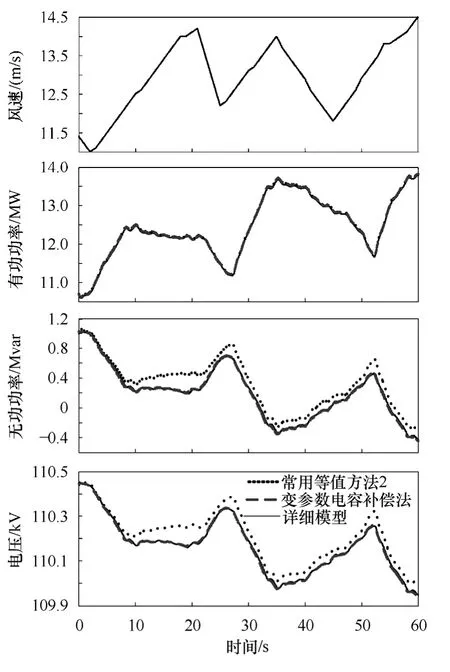
圖6 固定電容器補償風電場并網點的動態響應Fig.6 Dynamic response of wind farm at point of interconnection under fixed capacitor compensation

表3 等值方法的誤差Tab.3 Error of equivalence methods

從圖6 和表3 可以看出，變參數電容補償法的有功功率誤差、無功功率誤差分別為 1.51%和0.85%，而常用等值方法2的有功功率誤差、無功功率誤差分別為2.03%和為6.8%。仿真結果表明，變參數等值建模方法可有效降低其無功功率誤差，得到與風電場詳細模型基本一致的動態特性。有效解決了常用等值方法建立風電場模型的無功功率誤差問題。

為深入分析變參數電容補償法中三種措施（即補償風電機組無功誤差的變參數電容、補償機端電容器無功誤差的變參數電容以及等值電纜的充電電容）對降低誤差的貢獻大小，分別進行了只考慮一種措施的變參數電容補償法的仿真驗證。當僅考慮補償風電機組無功誤差的變參數電容時，無功功率誤差EQ為0.93%；當僅考慮補償機端電容器無功誤差的變參數電容時，無功功率誤差EQ為7.01%；當僅考慮等值電纜的充電電容時，無功功率誤差EQ為7.02%。從計算結果可以看出，變參數電容補償法中的第一項措施補償風電機組無功誤差的變參數電容對降低誤差起主要貢獻。當分別僅考慮第二、三項措施時，其無功功率誤差比常用等值方法2 略大，其原因是：

（1）與常用等值方法2 相比，第二、三項措施計算出來的變參數電容將會使等值模型發出更多的無功，而第一項措施計算出來的變參數電容為負，將會使等值模型吸收更多的無功。

（2）從圖6的無功功率可以看出，常用等值方法2 建立模型的輸出無功功率大于風電場詳細模型的輸出無功功率，因此當分別僅考慮第二、三項措施時，無功功率誤差會更大，當僅考慮第一項措施時，無功功率誤差會減小。但并不是第二、三項措施不重要，當風機間電纜長度增加、風電場內機組較多導致風機機端電壓差距較大時，第二、三項措施對降低誤差的貢獻將會增大。

5.3 機端按分組投切電容器補償

由于目前有關機端采用分組投切電容器補償的風電場等值建模方法研究較少，因此本文主要比較風電場詳細模型與本文提出的風電場變參數模型。采用與機端按固定電容器補償風電場算例相同的結構和相同的輸入風速等仿真條件，不同點是機端補償方式為分組投切電容器，其控制規律見表1。圖7 給出了風電場詳細模型和變參數電容補償等值方法的模型在并網點A 有功功率、無功功率以及電壓的動態響應過程曲線。

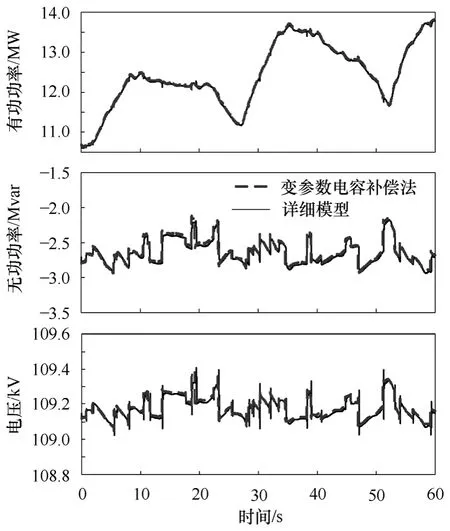
圖7 分組投切電容器補償風電場并網點的動態響應Fig.7 Dynamic response of wind farm at point of interconnection under grouping switching capacitor compensation

從圖7 可以看出，采用變參數電容補償法建立的等值模型得到了與風電場詳細模型基本一致的動態響應，從而證實了該等值方法可應用于機端按分組投切電容器補償的風電場動態等值建模。

6 結論

針對風速波動下常用風電場等值方法建立的模型存在無功功率誤差問題，提出了一種變參數等值建模方法。分別給出了兩種無功補償方式的風電場等值模型結構及其變參數電容的計算方法。并深入分析了變參數等值建模方法中各種措施對降低無功功率誤差的貢獻大小。仿真結果表明，該方法可有效降低等值模型的無功功率誤差，得到與風電場詳細模型基本一致的動態特性。

[1]Hector A Pulgar Painemal，Peter W Sauer.Towards a wind farm reduced-order model[J].Electric Power Systems Research,2011,81(8):1688-1695．

[2]Jacques Brochu,Christian Larose,Richard Gagnon.Validation of single-and multiple-machine equivalents for modeling wind power plants[J].IEEE Transactions on Energy Conversion,2011,26(2):532-541.

[3]陳樹勇,王聰,申洪,等.基于聚類算法的風電場動態等值[J].中國電機工程學報,2012,32(4):11-19.Chen Shuyong,Wang Cong,Shen Hong,et al.Review on equivalent modeling for large-scale wind power field[J].Proceedings of the CSEE,2012,32(4):11-19.

[4]栗然,唐凡,劉英培,等.基于自適應變異粒子群算法的雙饋風電機組等值建模[J].電力系統自動化,2012,36(4):22-27.Li Ran,Tang Fan,Liu Yingpei,et al.Equivalent model of doubly-fed wind turbine generator systems based on auto mutation particle swarm optimization algorithm[J].Automation of Electric Power Systems,2012,36(4):22-27.

[5]李光允,陳小虎,唐國慶.大型風力發電場等值建模研究綜述[J].華北電力大學學報,2006,33(1):42-46.Li Guangyun,Chen Xiaohu,Tang Guoqing.Review on equivalent modeling for large-scale wind power field[J].Journal of North China Electric Power University,2006,33(1):42-46.

[6]曹娜,趙海翔,陳默子,等.潮流計算中風電場的等值[J].電網技術,2006,30(9):53-56.Cao Na,Zhao Haixiang,Chen Mozi,et al.Equivalence method of wind farm in steady-state load flow Calculation[J].Power System Technology,2006,30(9):53-56.

[7]包能勝,徐軍平,倪維斗,等.大型風電場失速型機組等值建模的研究[J].太陽能學報,2007,28(11):1284-1289.Bao Nengsheng,Xu Junpin,Ni Weidou,et al.Investigation of equivalent modeling of multiple stall wind turbine system on larges scale wind farm[J].Acta Energiae Solaris Sinic,2007,28(11):1284-1289.

[8]孫建鋒,焦連偉,吳俊玲,等.風電場發電機動態等值問題的研究[J].電網技術,2004,28(7):58-61.Sun Jianfeng,Jiao lianwei,Wu Junling,et al.Reserch on multi-machine dynamic aggregation in wind farm[J].Power System Technology,2004,28(7):58-61.

[9]米增強,蘇勛文,楊奇遜,等.風電場動態等值模型的多機表征方法[J].電工技術學報,2010,25(5):162-169.Mi Zengqiang,Su Xunwen,Yang Qixun,et al.Multimachine representation method for dynamic equivalent model of wind farms[J].Transactions of China Electrotechnical Society,2010,25(5):162-169.

[10]米增強,蘇勛文,余洋,等.雙饋機組風電場動態等值模型研究[J].電力系統自動化,2010,34(17):72-77.Mi Zengqiang,Su Xunwen,Yu Yang,et al.Study on dynamic equivalence model of wind farms with doubly fed induction generator wind turbines[J].Automation of Electric Power Systems,2010,34(17):72-77.

[11]喬嘉賡,魯宗相,閔勇,等.風電場并網的新型使用等效方法[J].電工技術學報,2009,24(4):209-213.Qiao Jiageng,Lu Zongxiang,Min Yong,et al.New dynamic equivalence method for grid-connected wind farm[J].Transactions of China Electrotechnical Society,2009,24(4):209-213.

[12]風電場接入電網技術規定實施細則[S].國家電網公司,2009.

[13]蘇勛文,米增強,王毅.風電場常用等值方法的適用性及其改進研究[J].電網技術,2010,34(6):175-180.Su Xunwen,Mi Zengqiang,Wang Yi.Study on applicability and improvement of wind farm common equivalent methods[J].Power System Technology,2010,34(6):175-180.

[14]黃梅,萬航羽.在動態仿真中風電場模型的簡化[J].電工技術學報,2009,24(9):147-152.Huang Mei,Wang Hangyu.Simplification of wind farm model for dynamic simulation[J].Transactions of China Electrotechnical Society,2009,24(9):147-152.

[15]Perdana A,Uski Joutsenvuo S,Carlson O,et al.Comparison of an aggregated model of a wind farm consisting of fixed-speed wind turbines with field measurement[J].Wind Energy,2008,11(1):13-27.

[16]Trudnowski D J,Gentile A,Khan J M.Fixed-speed wind-generator and wind-park modeling for transient stability studies[J].IEEE Transactions on Power Systems,2004,19(4):1911-1917.

[17]Shafiu A,Anaya-Lara O,Bathurst G.Aggregated wind turbine models for power system dynamic studies[J].Wind Engineering,2006,30(3):171-186.

[18]Fernández L M,Saenz J R,Jurado F.Dynamic models of wind farms with fixed speed wind turbines[J].Renewable Energy,2006,31(8):1203-1230.

[19]Akhmatov V,Knudsen H.An aggregate model of a grid-connected,large-scale,offshore wind farm for power stability investigations-importance of windmill mechanical system[J].Electrical Power Energy Systems,2002,24(9):709-717.

[20]倪以信,陳壽孫,張寶霖.動態電力系統的理論與分析[M].北京:清華大學出版社,2002.