基于預測無差拍算法的永磁同步發電機無傳感器控制

童 力 鄒旭東 豐樹帥 黃清軍 張 允 康 勇

（1.華中科技大學強電磁工程與新技術國家重點實驗室 武漢 430074 2.湖南省電力公司供電服務中心 長沙 410007）

1 引言

風能因其可大規模開發和無污染利用，而被廣泛視作傳統化石能源發電應用的替代能源[1,2]。當前，主流的風力發電技術包括雙饋式和直驅式，而適應更低轉速[3]的永磁同步發電機（PMSG）使直驅式風力發電系統在省卻齒輪箱的同時，呈現出高效、可靠以及出色的電網故障適應性[4,5]，因而極具應用前景。為實現PMSG的高效運行，常用光電編碼器或旋轉變壓器為其高性能矢量控制提供精確的轉子位置和轉速信息。但隨著風電機組功率等級和機械尺寸的提升，機械式傳感器變得難以安裝且極易受工作環境干擾，運行可靠性大幅降低、甚至會影響到發電機組的安全與穩定運行。為此，研究PMSG的無傳感器控制技術具有十分重要的理論意義和工程應用價值[6,11]。

永磁同步發電機的無傳感器控制需要觀測轉子的位置和轉速，來參與發電機的磁場定向與速度反饋控制。一方面，基于高頻信號注入的觀測方法[6]利用電機的凸極效應在轉速低至零時仍可實現觀測，但局限于凸極電機，且額外引入的高頻信號會降低電機的控制性能。另一方面，基于反電動勢的觀測方法[7,9]，其本身具備出色的動靜態性能，但在極低轉速時難以滿足觀測精度。考慮到實際風力機組僅在切入風速以上發電運行，PMSG 無需零速啟動且不會運行在過低的轉速區域，本文提出基于估算反電動勢的同步鎖相環（SRF-PLL）技術[10,11]，來觀測轉子的位置角和轉速以實現無傳感器控制。

一般地，反電動勢的估算精度依賴于電機模型參數和定子電流的跟蹤控制性能，并影響著PMSG無傳感器控制的整體性能。在數字控制系統中，由電流采樣、占空比更新和死區等因素引起的控制延遲[12]，會降低系統的控制性能，而電機參數的變化會使性能進一步惡化。為此，需要有效的定子電流環控制方案，以適應控制延遲和參數時變對控制性能造成的影響。目前，PMSG的電流控制方法主要包括：滯環控制、同步旋轉坐標系下的PI 控制和預測控制。滯環控制實現簡單、動態性能好[13]，但開關頻率不確定且存在較大的電流跟蹤誤差。同步旋轉坐標系下的PI 控制具有出色的穩態跟蹤性能，但受制于帶寬限制、動態性能較差，需要額外的延時補償來提高電流環的性能[12,14]。相比較而言，預測控制可以得到更出色的動態響應和穩態跟蹤性能。其中，基于目標函數直接確定變換器開關動作的直接預測控制[10,15,16]，電流響應速度快，但較高的實時性要求和受效率限制的開關頻率降低了其控制性能，會產生較大的電流紋波；而根據預測方程得到電流跟蹤所需的電壓指令，并結合空間矢量調制（SVPWM）技術將電壓指令轉換成開關狀態的無差拍控制[17-19]，可有效減少算法對實時性的要求，并具有較好的動態性能和較小的電流紋波。

本文在建立永磁同步發電機數學模型的基礎上，利用電流控制器生成的定子電壓指令實現反電動勢的估算后，給出了基于SRF-PLL的轉子位置與轉速的觀測模型。為了獲得優異的無傳感器控制性能，本文提出了一種預測無差拍控制算法：通過對估算反電動勢進行串聯補償再引入到無差拍控制器中，改善系統穩定性的同時，實現了定子電流的無靜差跟蹤；在此基礎上，基于Luenberger 算法對定子電流超前預測以補償數字控制一拍滯后的影響，并在維持系統穩定性的前提下，根據離散控制模型設計控制器參數，改善了定子電流環的動態響應及其適應電機參數變化的魯棒性。最后，通過仿真和實驗證明了本文所提控制方案的有效性及其在實際風力發電應用中的可行性。

2 系統拓撲與數學建模

2.1 系統拓撲結構

基于永磁同步發電機的直驅式風力發電系統結構如圖1 所示。風力機與PMSG（表貼式或內置式）同軸相連，并通過由公共直流環節耦合形成背靠背結構的并網變流器連接至電網。通常，只有當檢測到預設的切入風速時，接觸開關K1導通，并同時啟動機側變換器（Generator Side Converter,GSC）對PMSG 實施相應的控制策略進行風能捕獲。與此同時，經由LC 濾波器和隔離變壓器連接于電網的網側變換器（Network Side Converter,NSC）則始終維持直流母線電壓的恒定，以實現高質量的電能傳輸以及所需的無功補償。本文將針對直驅風力發電系統中PMSG的無傳感器控制技術進行理論分析和實驗研究。

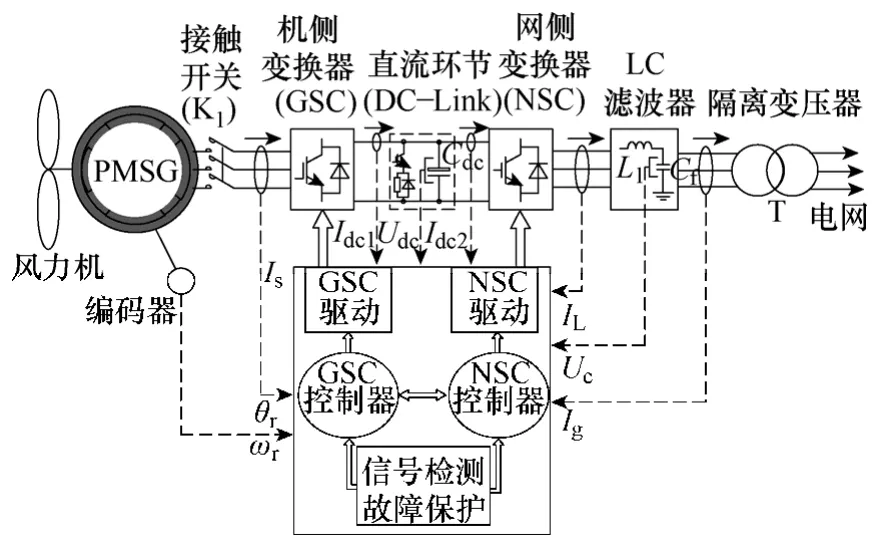
圖1 基于永磁同步發電機的直驅風力發電系統結構Fig.1 System structure of PMSG-based driect-driven wind power generation system

2.2 PMSG的離散域數學模型

一般地，永磁同步發電機的高性能矢量控制是在轉子位置角參與同步定向的旋轉坐標系下實施的。取定子電流矢量為Is(t)=[Isd(t)Isq(t)]T，反電動勢矢量為Es(t)=[Esd(t)-Esq(t)]T以及定子端電壓矢量為ur(t)=[urd(t)urq(t)]T，式中下標d 和q 表示在旋轉坐標系下所對應的狀態量。于是，選擇定子電流為狀態變量，得到PMSG 在同步定向后的連續域狀態空間模型為

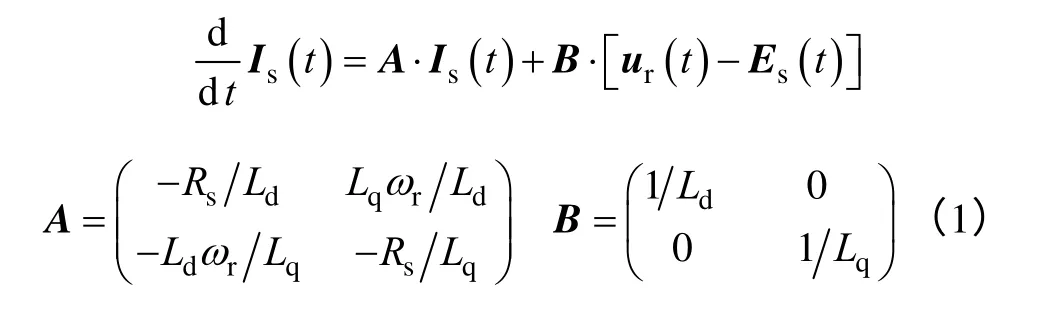
式中ωr——轉子的電氣角速度；

Rs——定子相電阻；

Ld，Lq——交、直軸同步電感。

忽略數字采樣過程中的延遲，由式(1)求解出連續時間狀態的定子電流可表示為

取離散采樣時間分別為t0=kTs和t=(k+1)Ts，可以得到離散時間狀態的定子電流為

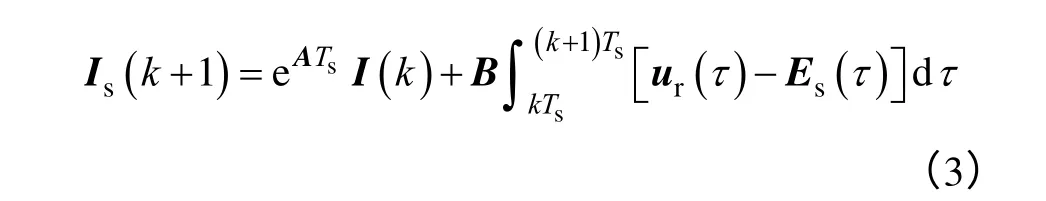
式中，“k”代表離散的采樣時間點，k=1,2,3,…,n。

在系統采樣周期Ts較小的情況下，同步旋轉坐標系中的反電動勢矢量Es和定子端電壓矢量ur在kTs～(k+1)Ts的時間間隔內可近似視作恒定，于是

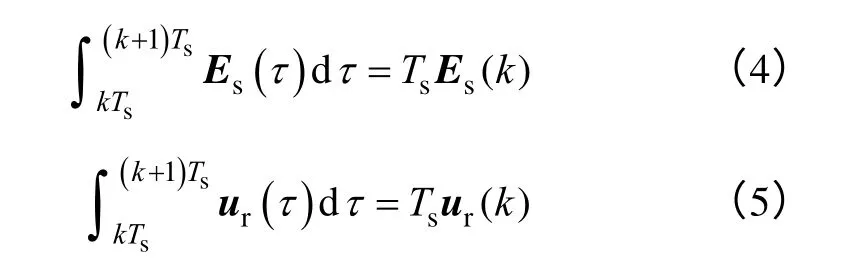
聯立式（3）～式（5）并結合泰勒級數展開式，得到PMSG 離散域狀態空間模型如下：

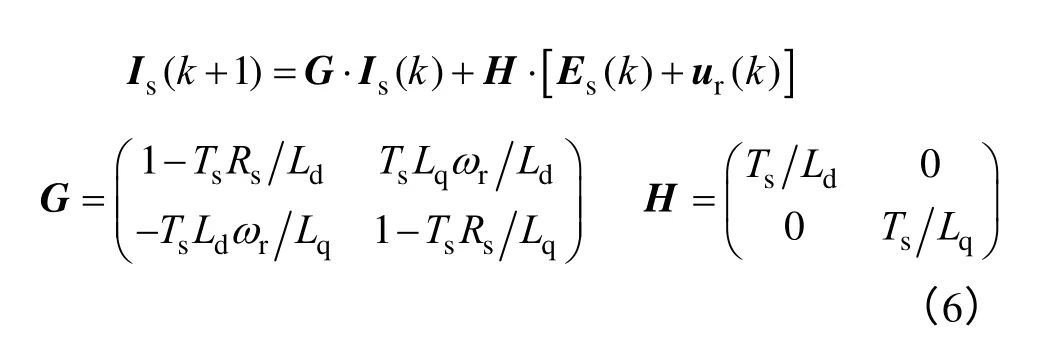
于是，根據式（6）可以執行基于電機模型的反電動勢估算，以實現轉子位置角和轉速的觀測。

3 基于SRF-PLL的無傳感器觀測算法

當PMSG 在永磁體磁場定向的參考坐標系下采取“零d 軸電流控制”策略時[20]，電磁轉矩與定子q 軸電流間的正比例關系將使得發電機呈現出如直流電機般出色的控制性能。因此，無傳感器控制方案的實現，首先需要觀測轉子的位置角。圖2 所示為實際磁場定向的γ-Δ參考坐標系與觀測的d-q 軸參考坐標系的空間矢量圖。其中，兩個旋轉坐標系分別以電氣角速度ωr和ωe旋轉。

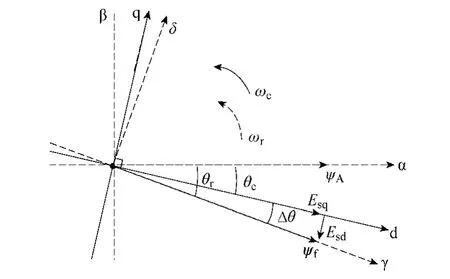
圖2 實際與觀測的同步定向坐標系空間矢量圖Fig.2 Space vector diagram with actual and observed synchronized orientation frames

圖2 中，θr和θe分別代表著實際的和觀測的轉子位置角。初始階段，兩者間存在一定的角度誤差（即Δθ≠0）。此時，觀測定向參考坐標系下的d-q軸反電動勢Esd和Esq，實際是由永磁體磁通量ψf所確定的反電動勢空間矢量投影所得，因而可得到其d 軸分量Esd與觀測誤差角Δθ之間近似相等的關系。因此，可將Esd作為同步鎖相環的反饋輸入，并通過 PI 控制器來調節觀測輸出的轉子位置角θe，使Esd趨近于零（即Δθ≈0），實現轉子信息的無傳感器觀測。為了避免直接采樣PWM 波形狀的定子端電壓，本文利用電流控制器生成的電壓指令來參與基于電機模型的反電動勢估算。于是，在觀測定向的d-q 坐標系下，基于電機模型參數新生成的系數 矩陣Jm和1m-H，得到估算的反電動勢矢量如下：

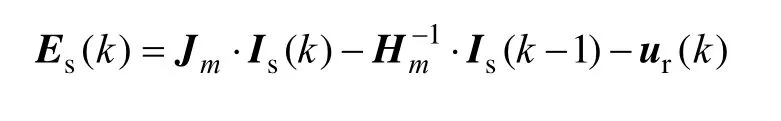
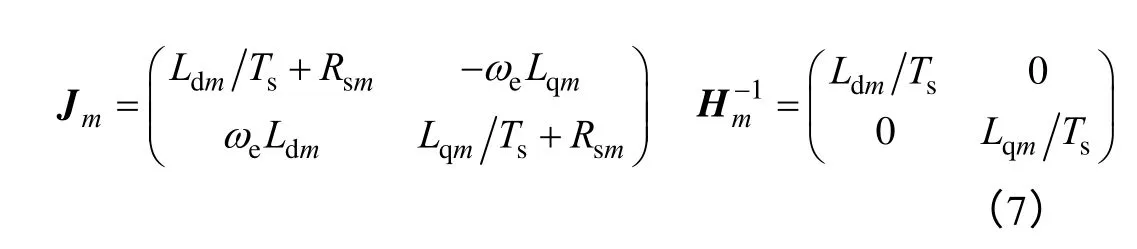
式中，“m”定義為測量的與實際電機參數間的比值，即m=Lm/L=Rsm/Rs。

取式（7）中的d 軸分量Esd作為反饋，并進一步將基于q 軸反電動勢Esq的前饋控制量式（8）疊加至PI 控制器的輸出。最終，得到觀測的轉子電氣角速度，如式（9）所示。

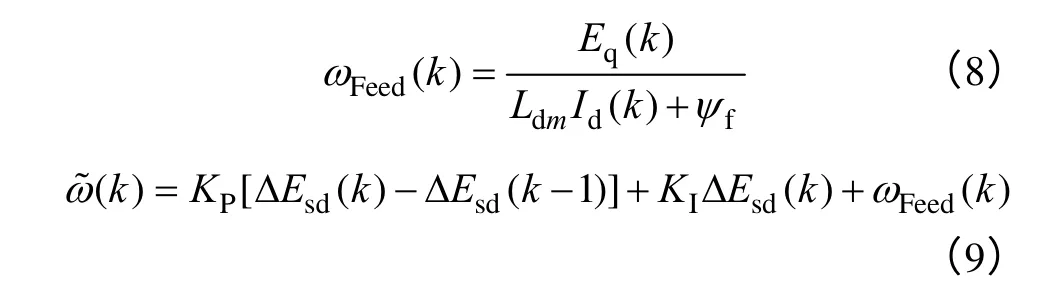
式中Kp和KI——鎖相環PI 控制器的比例和積分 控制系數；

ΔEsd——d 軸反電動勢的估算誤差。

事實上，基于式（9）的觀測轉速已包含轉子的位置角信息，但也同時存在著高頻噪聲[10]。為此，常采用低通濾波器（LPF）濾除式（9）中的高頻分量后再對其進行積分運算，得到轉子位置角觀測的離散狀態表達式為

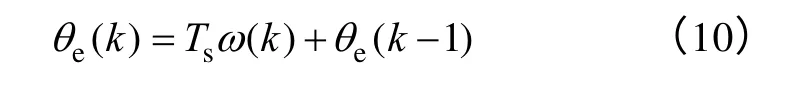
根據式（7）～式（10），可以得到基于反電動勢估算、采用SRF-PLL的無傳感器觀測模型，如圖3 所示。當選取適當的PI 控制器和低通濾波器參數，便可有效地改善該觀測方法的動態響應、擾動抑制能力及其他系統響應特性[10]。

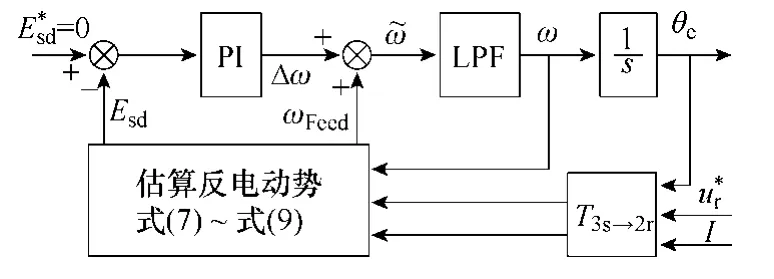
圖3 基于SRF-PLL的無傳感器觀測模型原理框圖Fig.3 Block diagram of SRF-PLL based sensor-less observation model

盡管鎖相環本身具備出色的動態響應特性，但轉子位置角的觀測很大程度上還將由反電動勢的估算精度所決定。通過與精確磁場定向和無靜差定子電流跟蹤控制下的參考反電動勢相比較，近似得到觀測誤差角Δθ的表達式為

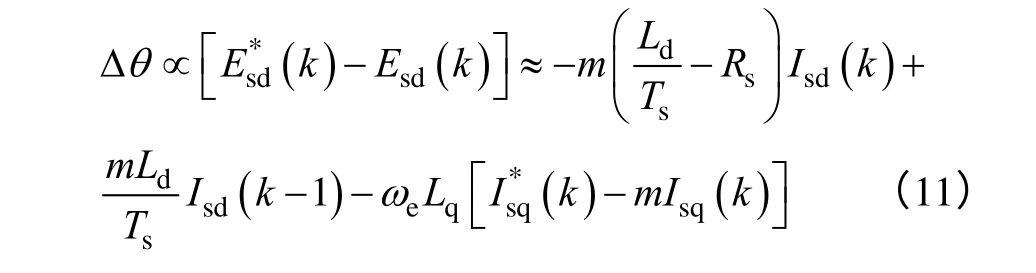
式中，上標“*”表示參考指令值。

通過式（11）可以看到，在基于反電動勢估算的SRF-PLL 無傳感器觀測方法中，轉子位置角的觀測精度是由電機模型參數和定子電流的跟蹤控制所決定，而轉子的位置角與其轉速緊密相關。因此，在準確測量電機參數的前提下（即m=1.0 時），定子電流出色的靜態跟蹤特性（即）將能夠實現觀測誤差的最小化控制。

4 魯棒的預測無差拍電流控制

期望在下個控制周期(k+1)Ts結束之前實現電流指令跟蹤的無差拍控制器，無疑將使無傳感器控制的PMSG 呈現出優異的動靜態響應特性。首先，為了實現定子電流的無靜差跟蹤，引入式（7）中的估算反電動勢，并由此得到當前時刻kTs的電壓控制指令表達式為

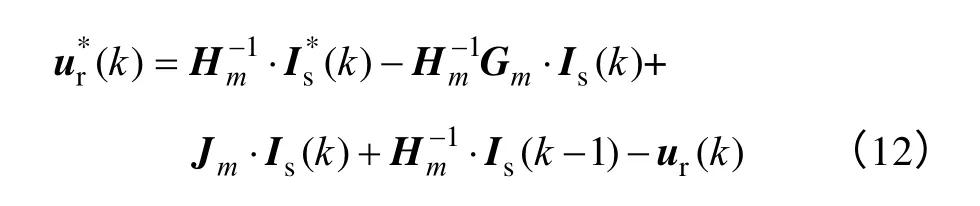
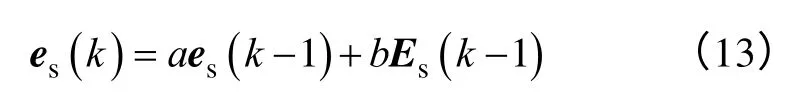
式中，a和b是串聯補償器的控制系數。

于是，由式（12）、式（13）可得到新的無差拍電壓控制指令為

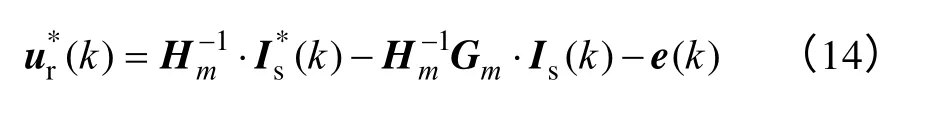
考慮數字控制的一拍滯后，基于式（7）、式（13）和式（14）可得到如圖4 所示的采用串聯補償器的無差拍控制系統模型。

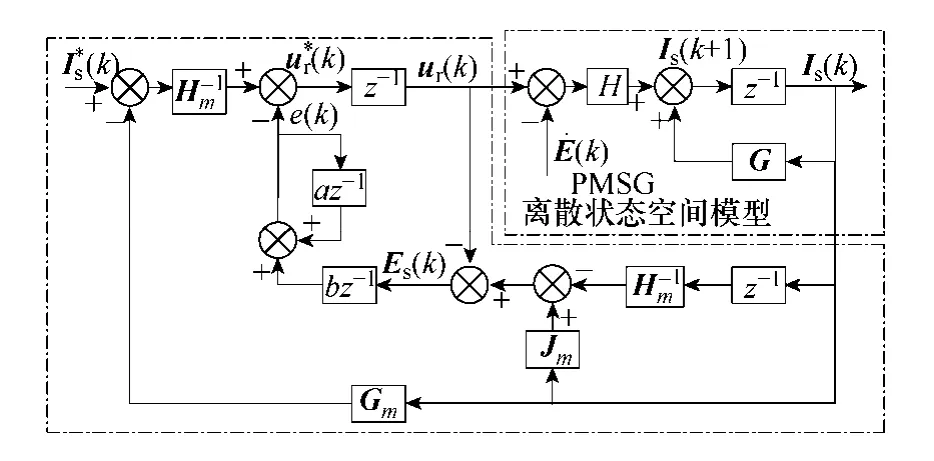
圖4 帶有串聯補償器的無差拍控制系統模型Fig.4 Model of dead-beat algorithm based control system with the cascade compensator

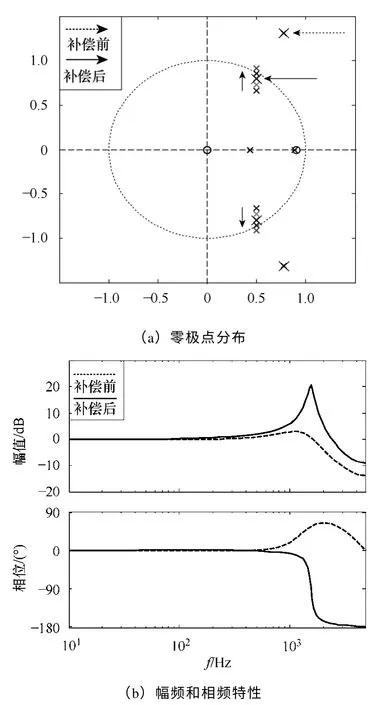
圖5 有、無串聯補償器的無差拍控制系統閉環特性分析Fig.5 Closed-loop characteristics of dead-beat control based system with or without compensator

在不考慮電機參數變化的前提條件下（即m=1.0 時），串聯補償前、后的無差拍控制系統閉環特性如圖5 所示。圖5a 中，補償前的系統閉環主導 極點處在遠離單位圓之外的位置，而補償后的主導極點將回到單位圓內。但此時系統的主導共軛極點十分靠近單位圓，這意味著惡劣的動態響應以及匱乏的穩定裕度。此外，如圖5b 中系統的閉環頻率響應特性所示，盡管能夠在低頻段實現零增益、零相移的控制特性，但額外引入的諧振峰還可能在定子電流中產生一定諧波分量，進而造成電機控制性能的下降。

通過上述分析可知，需要補償滯后一拍對電流環動、靜態響應特性的影響，尤其是當電機參數發生變化時，進一步提高PMSG 無傳感器控制的魯棒性。為此，在對估算反電動勢引入串聯補償器的基礎上，本文基于Luenberger 算法[19]對定子電流進行一拍超前預測，得到預測電流的表達式為

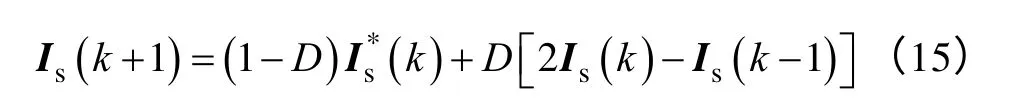
式中，系數D定義為預測權值，并設定在[0,1]的范圍內變化。

將超前預測的定子電流Is(k+1)代入式（14）中，得到基于預測無差拍算法的電壓控制指令為

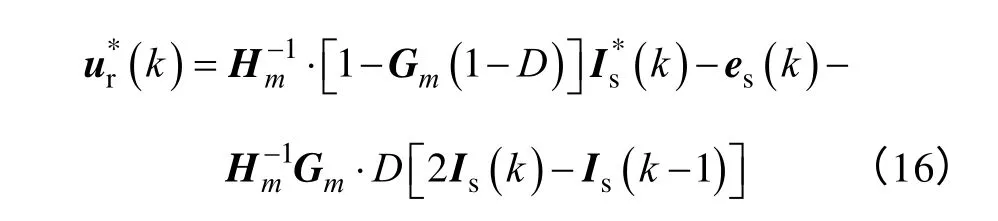
同樣地，結合式（7）、式（13）和式（16），在觀測的d-q 參考坐標系下，可以進一步得到基于預測無差拍算法的系統控制模型，如圖6 所示。

圖6 基于預測無差拍控制算法的系統模型Fig.6 Model of predictive dead-beat algorithm based control system

通過離散傳遞函數的推導，可知圖6 中所示的控制模型是一個四階系統，其響應特性很大程度上是由預測權值“D”和電機參數的變化程度“m”所共同決定的。近似忽略所有的無窮小項，得到簡化后的閉環系統特征方程表達式為

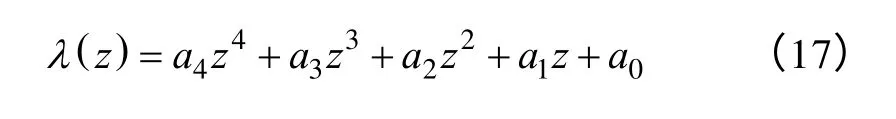
式中，a4=1；a3=–(1+a)；a2=2Dm+a–b；a1=b–(2a+1)Dm+bm；a0=aDm–bm。

于是，在保證系統穩定性的前提條件下，通過Juri 判據將能夠分析得到本文預測無差拍控制算法的魯棒性能，即不同預測權值“D”所能夠適應的電機參數變化范圍“m”，如圖7a 所示。可以看到，圖中所示的陰影區域界定了預測無差拍控制算法適應電機參數變化的穩定運行范圍，其單調遞減的曲線特性表明選取較小的預測權值“D”將使控制系統具有更出色的魯棒性。

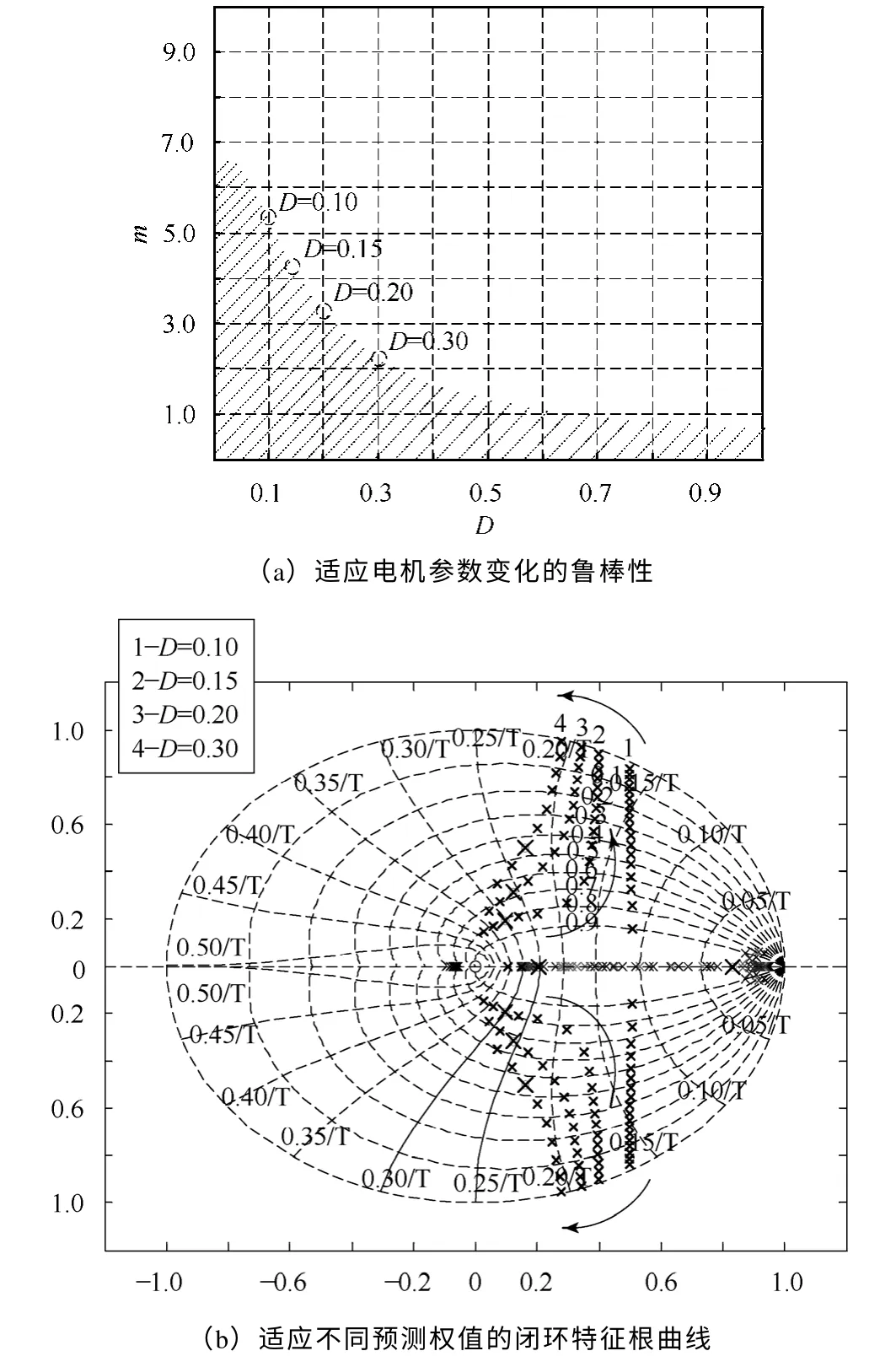
圖7 基于預測無差拍控制的閉環特性分析Fig.7 Closed-loop characteristics of predictive dead-beat algorithm based control system

不過，由圖7b 中所示系統的閉環特征根曲線圖可知，過分優化的電機參數魯棒性反而會降低系統的動態響應速度。伴隨著預測權值“D”的增大，系統的特征根曲線將移向高帶寬區域，此時系統的動態響應速度得到提高，但適應的電機參數變化也會隨之減小。因此，預測無差拍控制參數的設計，需要同時兼顧系統的動態響應和適應電機參數變化的魯棒性能。

事實上，在長期的運行過程中，電機參數的變化趨勢通常無法預測。因此，本文建議：優化選取的預測權值“D”能夠在±50%的電機參數變化范圍內（即m=[0.5,1.5]），滿足定子電流控制對動態響應和魯棒性能的要求。于是，本文取D=0.3，并由此得到系統的閉環頻率響應Bode 圖，如圖8 所示。

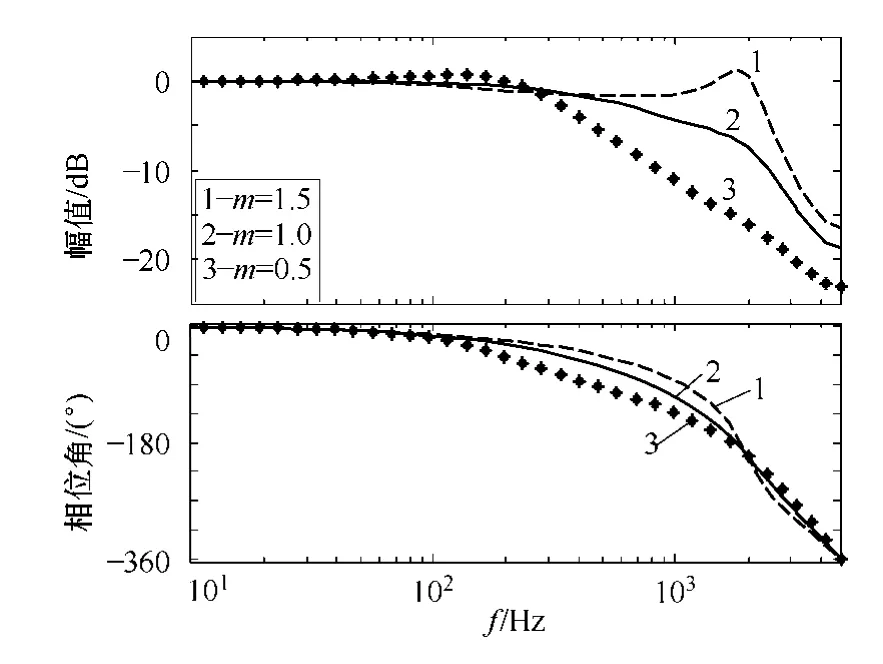
圖8 不同電機參數條件下的閉環頻率響應曲線Fig.8 Closed-loop frequency responses with vaired motor parameters

為了進一步實現PMSG的無傳感器速度反饋調節，基于式（13）中串聯補償后的q 軸反電動勢，可得到觀測轉速的離散狀態表達式為

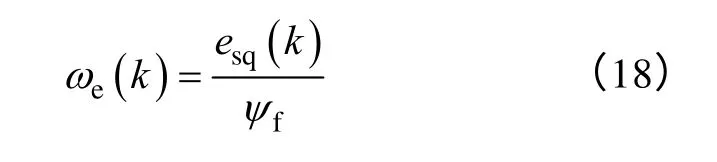
最后，在觀測定向的d-q 參考坐標系下，采用預測無差拍電流控制，并基于式（18）實現電機的轉速反饋，得到PMSG 完整的無傳感器控制方案原理框圖，如圖9 中所示。

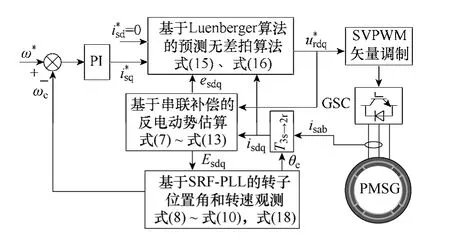
圖9 完整的PMSG 無傳感器控制原理框圖Fig.9 Complete block diagram of the sensor-less control schecme for the PMSG

5 實驗研究

5.1 試驗系統說明

為了驗證本文基于預測無差拍算法的無傳感器控制方案，如圖1 構建一套基于10kW PMSG的直驅發電試驗系統，參數見下表。系統中采用獨立調速的永磁同步電動機代替風力機，直接與PMSG 同軸相連，如圖10 所示，而直流母線電壓則由NSC建立并維持恒定，以使PMSG 能夠由GSC 實施正常的發電控制。

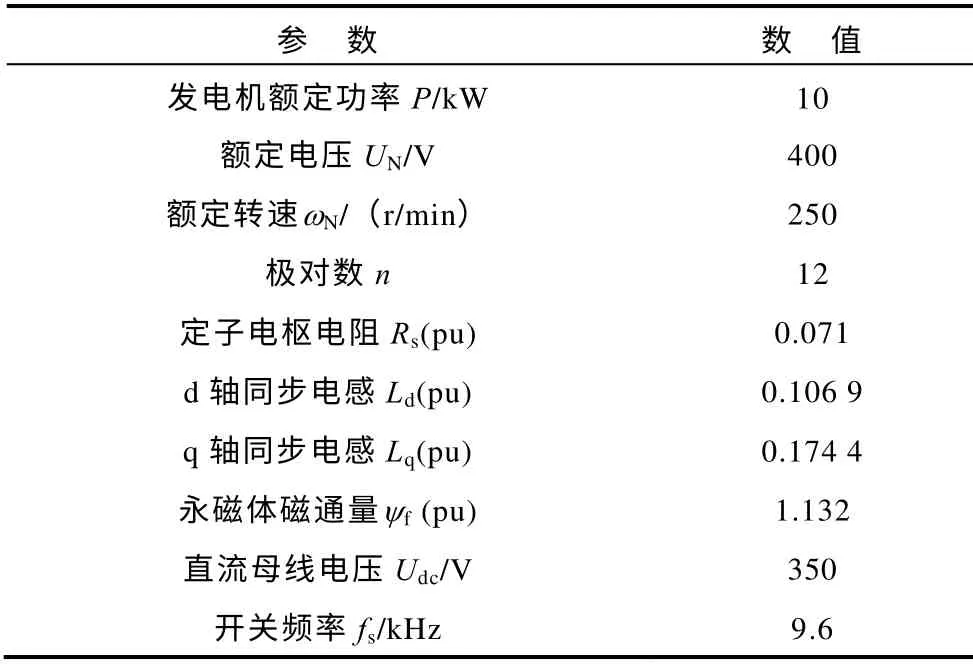
表 試驗系統的主要參數Tab. Main parameters of the experiment system

圖10 原動機與發電機的試驗模型Fig.10 Prototype of prime-motor and PMSG

控制單元以32 位浮點運算的TMS 320F 28335 DSP 為核心，并采集兩相定子電流和電壓分別實現控制與保護功能。PMSG 裝載的11 位光電編碼器，則作為本文無傳感器觀測算法的參考依據。在系統啟動以前，接觸開關K1隔離發電機組與并網變流器的連接，此時PMSG 由原動機帶動，在50r/min的初始轉速條件下空載運行。

5.2 基于預測無差拍的無傳感器控制實驗

在實驗過程中，根據精確測量的電機參數（即m=1.0）和優化設計的控制器（D=0.3），實現如圖9中所示的方案。考慮到原動機的轉速由其調速裝置獨立調節的，無法完全模擬實際的風力機特性，但其足以驗證本文對PMSG 所提出的無傳感器控制。于是，首先在沒有轉速外環的條件下，通過人為設定PMSG的轉速和轉矩電流，得到PMSG 無傳感器控制的動靜態響應波形，如圖11～圖13 所示。

當電機空載運行在50r/min 時，閉合K1并以6A的轉矩電流啟動PMSG 進入發電狀態。如圖11 所示，SRF-PLL 在經過短暫的調節過程后，觀測到的轉子位置角θe迅速跟蹤編碼器輸出的參考位置角θr，考慮編碼器和D-A 芯片本身的精度，圖中示出的觀測誤差角近似為零（Δθ≈0），滿足對觀測精度的要求。于此同時，A、B 兩相定子電流幾乎沒有 超調地達到穩態，充分證明了本文預測無差拍控制出色的動態響應特性。隨后，將轉速和轉矩電流分別提高至100r/min 和10A，如圖12 所示，看到此時的觀測位置角θe與其參考θr基本重合，而通過FFT 分析，A、B 相定子電流的THD 分別為1.23%和1.42%，具有較好的靜態跟蹤性能。圖13 所示為估算反電動勢在α-β 坐標系下的李薩如圖，平滑的近似圓形間接驗證了本文無傳感器控制方案的出色性能。

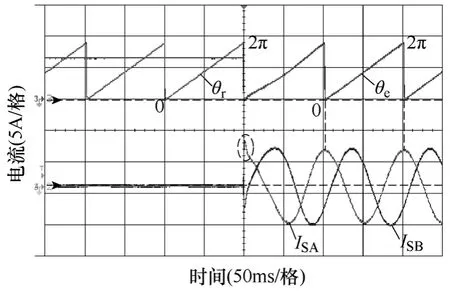
圖11 PMSG 無傳感器控制的動態響應波形Fig.11 Dynamic performance of the sensor-less vector controlled PMSG

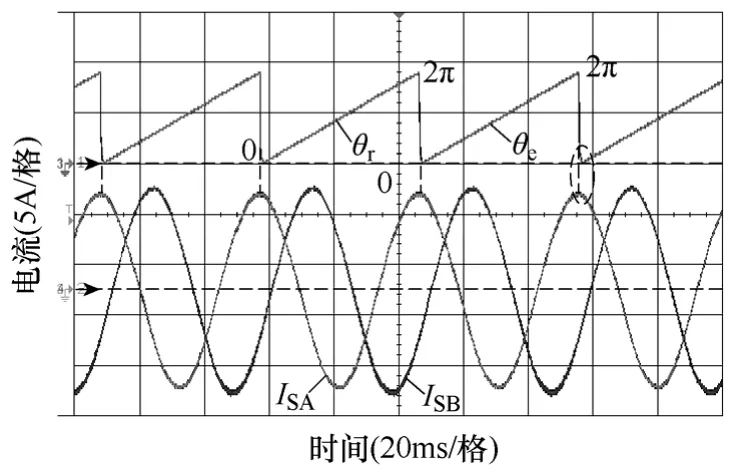
圖12 PMSG 無傳感器控制的靜態響應波形Fig.12 Static performance of the sensor-less vector controlled PMSG

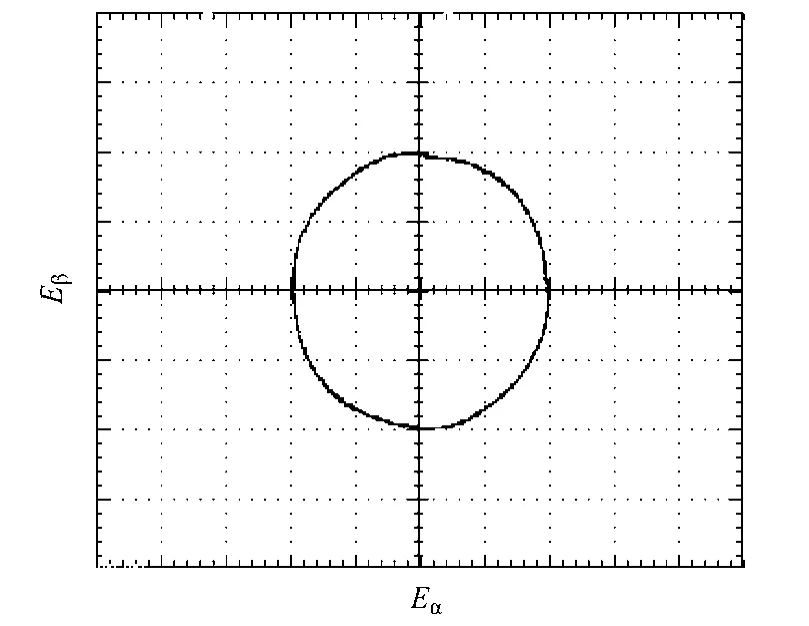
圖13 估算反電動勢在靜止α-β坐標系下的李薩如圖Fig.13 Lissajous figure of the estimated back EMF in stationary α-β frame

5.3 電機參數魯棒性實驗

在長期發電運行過程中，電機參數的變化不可避免、且無法預測，因而要求所采用的控制方案在一定范圍內對參數變化具有魯棒適應性。為此，本文采取主動改變電機模型參數的方式，包括交、直軸電感Ld和Lq,，以及電樞電阻Rs，使其發生±50%變化（即m=0.5 或1.5），以驗證控制方案的魯棒性。于是，當電機運行在100r/min，突然將轉矩電流由6A 增大至10A，得到增大（m=0.5）和減小（m=1.5）電機模型參數時PMSG的動態響應過程，分別如圖14a 和14b 所示。通過對比分析，除了θe與θr之間出現短暫的偏離過程，PMSG的無傳感器控制性能幾乎未受影響；而伴隨轉矩電流突減至6A，通過另一組魯棒性實驗波形，如圖15a 和15b 所示，也可以得到同樣的結論：即本文所提出的無傳感器控制方案具有出色的魯棒性能。

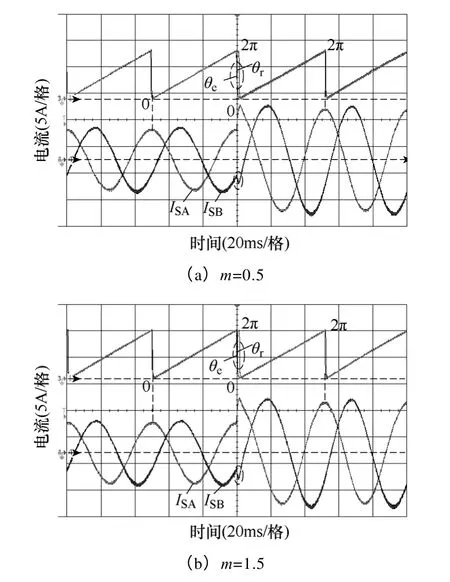
圖14 改變電機模型參數的魯棒性實驗：PMSG 突增 發電功率的動態響應Fig.14 Robustness experiments with varied motor parameters:dynamic performances by suddenly increased power generation

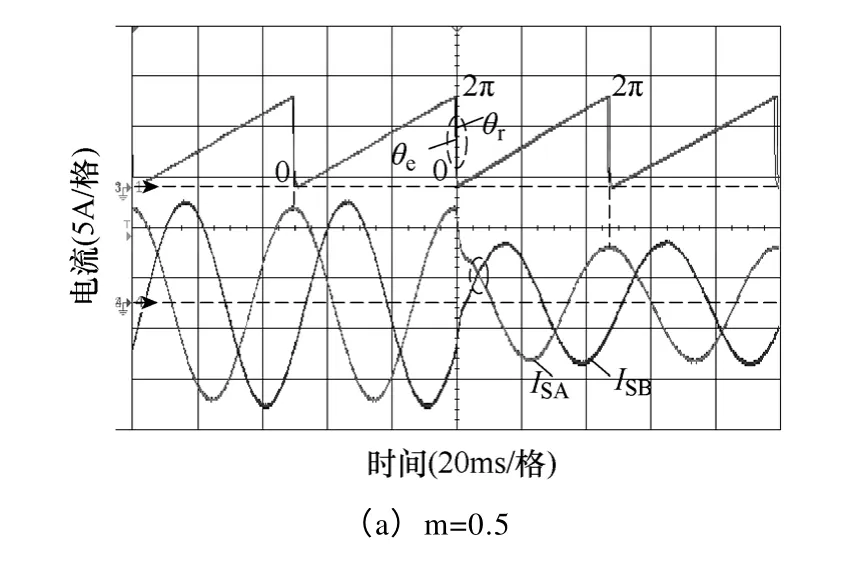
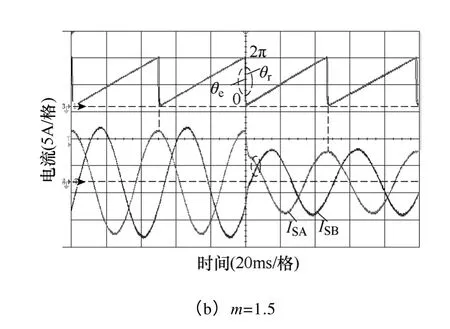
圖15 改變電機模型參數的魯棒性實驗：PMSG 突減 發電功率的動態響應Fig.15 Robustness experiments with varied motor parameters:dynamic performances by suddenly decreased power generation

隨后，在增大預測權值（即D=0.5）的條件下，使控制模型中的電機參數發生相同程度的變化（即m從1.0 升至1.5），將導致PMSG的異常運行，包括畸變的定子電流、觀測的轉子位置角θe及其參考值θr，如圖16 所示，這樣充分驗證了系統動態響應與魯棒性之間需要協調設計、合理兼顧。

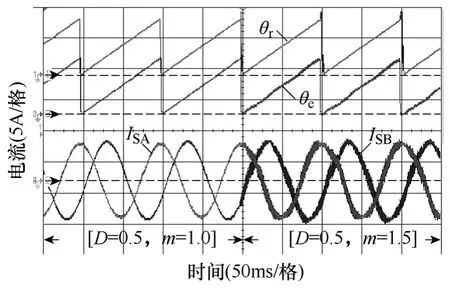
圖16 改變預測權值系數“D”的魯棒性實驗：突增 電機模型參數“m”的動態響應波形Fig.16 Robustness experiments with predictive weight value “D”:dynamic performances by suddenly increased motor parameters “m”

5.4 觀測轉速的反饋調節實驗

最后，加入觀測轉速反饋，進一步實現圖9 中所示完整的無傳感器控制方案，此時，原動機停止運行而僅作為大慣性環節，PMSG 則控制運行在電動狀態。當人為設定轉速指令由 30r/min 升高至150r/min 再回落至30r/min 時，得到PMSG 無傳感器控制的動態響應波形，如圖17 所示。由圖17 可以看到，基于觀測轉速ωme的反饋調節能夠快速、準確地實現速度指令跟蹤；而轉矩電流則在轉速的突變過程中，總是會快速上升至限幅值，以便增大電磁轉矩、加快轉速跟蹤的調節過程。而在完成速度跟蹤后，PMSG 又將以很小的轉矩電流來維持轉矩的平衡和速度的恒定，這也間接地證明了此時轉子位置角觀測的準確性。

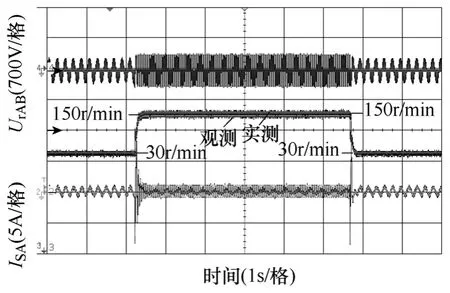
圖17 無傳感器控制PMSG的速度調節響應性能Fig.17 Speed regulation performance of the sensor-less controlled PMSG

6 總結

本文針對直驅風力發電系統中的永磁同步發電機提出了一套基于預測無差拍算法的無傳感器控制方案，通過深入的理論分析和實驗研究，可以得到以下結論：

（1）基于估算反電動勢、采用同步鎖相環的無傳感器觀測方法，能夠快速、準確地獲得轉子的位置角和轉速信息。

（2）預測無差拍控制算法使無傳感器控制的PMSG 呈現出優異的動靜態響應特性，并具有滿意的電機參數魯棒性能。

（3）最后，基于觀測轉速的速度反饋調節實驗充分證明了本文所提控制方案在實際直驅式風力發電系統中的可行性。

[1]Chinchilla M,Arnaltes S,Burgos J C,et al.Control of permanent-magnet generators applied to variable speed wind-energy systems connected to the grid[J].IEEE Transactions on Energy Conversion,2006,21(1):130-135.

[2]趙仁德,王永軍,張家勝.直驅式永磁同步風力發電系統最大功率追蹤控制[J].中國電機工程學報,2009,29(27):106-111.Zhao Rende,Wang Yongjun,Zhang Jiasheng.Maximum power point tracking control of the wind energy generation system with direct-driven permanent synchronous generators[J].Proceedings of the CSEE,2009,29(27):106-111.

[3]Spooner E,Williams A C.Direct coupled permanent magnet generators for wind turbine applications[J].IEE Electronic Power Application，1996，143(1)：1-8．

[4]Li H,Chen Z.Overview of different wind generator systems and their comparisons[J].IET Renewable Power Generation,2008,2(2):123-128.

[5]Hansen A D,Michale G.Multi-pole permanent magnet synchronous generator wind turbines’ grid support capability in uninterrupted operation during grid faults[J].IET Renewable Power Generation,2009,3(3):333-348.

[6]Bianchi N,Bolognai S,Jang Ji Hong,et al.Comparison of PM motor structures and sensorless control techniques for zero-speed rotor position detection[J].IEEE Transactions on Industry Electronics,2007,22(6):2466-2475.

[7]齊放,鄧智泉,仇志堅,等.一種永磁同步電機無速度傳感器的矢量控制[J].電工技術學報,2007,22(10):30-35.Qi Fang,Deng Zhiquan,Qiu Zhijian,et al.A method of sensorless vector control of PMSM[J].Transactions of China Electrotechnical Society,2007,22(10):30-35.

[8]Qiao W,Yang X,Gong X.Wind speed and rotor position sensorless control for direct-drive PMG wind turbines[J].IEEE Transactions on Industry Electronics,2012,48(1):3-11.

[9]Kim H,Son J B,Lee J Y.A high-speed sliding-mode observer for the sensor-less speed control of PMSM[J].IEEE Transactions on Industry Electronics,2011,47(3):1337-1343.

[10]Prendl M,Schaltz E.Sensorless model predictive direct current control using novel second-order PLL observer for PMSM drive systems[J].IEEE Transactions on Industry Electronics,2011,58(9):4087-4095.

[11]年珩,李嘉文,萬中奇.基于參數在線辨識的永磁風力發電機無位置傳感器控制技術[J].中國電機工程學報,2012,32(12):146-154.Nian Heng,Li Jiawen,Wan Zhongqi.Sensor-less control technique of PMSG for wind power application based on on-line parameter identification[J].Proceedings of the CSEE,2012,32(12):146-154.

[12]王宏佳,楊明,牛里,等.永磁交流伺服系統電流環帶寬擴展研究[J].中國電機工程學報,2010,30(12):56-62． Wang Hongjia,Yang Ming,Niu Li,et al.Current loop bandwidth extension for permanent magnet AC servo system[J].Proceedings of the CSEE,2010,30(12):56-62.

[13]Ho C N,Cheung V,Chung H S H.Constant-frequency hysteresis current control of grid-connected VSI without bandwidth control[J].IEEE Transactions on Power Electronics,2009,24(11):2484-2495.

[14]Kim K H,Youn M J.A simple and robust digital current control technique of a PM synchronous motor using time delay control approach[J].IEEE Transactions on Power Electronics,2001,16(1):72-82.

[15]Rodriguez J,Pontt J,Silva C A,et al.Predictive current control of a voltage source inverter[J].IEEE Transactions on Industrial Electronics,2007,54(1):495-503.

[16]Cortes P,Kazmierkowski M,Kennel R,et al.Predictive control in power electronics and drives[J].IEEE Transactions on Industrial Electronics,2008,55(12):4312-4324.

[17]Morel F,Shi X F Lin,Retif J M,et al.A comparative study of predictive current control schemes for a permanent magnet synchronous machine drive[J].IEEE Transactions on Industry Electronics,2009,56(7):2715-2728.

[18]Huerta J M E,Moreno J C,Fischer J R,et al.A synchronous reference frame robust predictive current control for three-phase grid-connected inverters[J].IEEE Transactions on Industry Electronics,57(3):956-962.

[19]Huerta J M E,Castello J,Gil R G,et al.An adaptive robust predictive current control for three-Phase grid-connected inverters[J].IEEE Transactions on Industry Electronics,58(8):3537-3546.

[20]陳榮.永磁同步電機的控制系統[M].北京:中國水利水電出版社,2009.