θ型奇異積分算子在加權Morrey空間中的有界性

葉曉峰，王騰飛，胡媛媛，王 蒙

（華東交通大學基礎科學學院，江西南昌330013）

算子在加權Lebesgue空間Lp(w)有界問題可以追溯到1972年Muckenhoupt在1972年文[1]中對Har?dy-Littlewood極大算子的討論。文中提出了Ap權的概念，由此順利解決了極大算子的加權有界性，并且使得加權理論如今成為調和分析的主要分支之一。2009年，Komori和Shirai在文[2]中首次提出了加權Mor?rey空間的概念，他們在文中討論了極大算子以及Calderón-Zygmund奇異積分算子、分數次積分算子及其交換子在加權Morrey空間中的有界性。最近出現了很多這方面的結果，具體參見文獻[3-8]。另外加權Morrey空間在偏微分方程中的應用，也得到了相應的推廣，詳見參考文獻[9]。

奇異積分算子尤其是Calderón-Zygmund奇異積分算子在各種函數空間中的有界性的討論是當代調和分析研究的主要問題。1952年，Calderón和Zygmund將這一算子推廣到了Rn上，他們運用實變方法解決了算子在Lebesgue空間Lp(Rn)的有界性問題從而使調和分析在高維空間中有了新的發展。1985年，Yabuta在文[10]中首次提出了θ型奇異積分算子，并得到了Lp有界性， 1＜p＜∞。最近文[11]討論了θ型奇異積分算子Lipschitz有界性的一個等價條件。另一方面，Hyt?nen在文[12]得到了θ型Calderón-Zygmund奇異積分算子在加權Lebesgue空間中的L2(w)有界性，并指出其最優上界為C(n，T，2)[w]A2。

2 定理及其證明

首先，我們來介紹加權Morrey空間的定義

定義1設1＜p＜∞，0＜κ＜1，w是權函數，對于Rn中的局部可積函數f(x)若滿足，則稱f(x)屬于加權Morrey空間，并記其范數為

注意到當κ=0時，Lp，0(w)=Lp(w)是對經典的加權Lebesgue空間的推廣。下面給出Ap權的如下定義

定義2設1＜p＜∞，若存在常數C≥1使得對于任意的正方體Q有

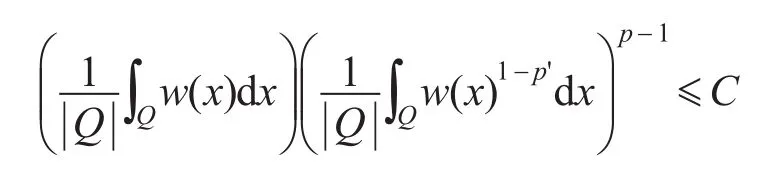
為了介紹θ型Calderón-Zygmund奇異積分算子，先給出連續模的定義。

定義3設θ(0)=0，稱θ:[0，∞)→[0，∞)是一個連續模，若θ是次可加的，即θ(t+u)≤θ(t)+θ(u)，并且單調遞增。

從而可以定義θ型Calderón-Zygmund奇異積分算子為

定義4設θ(t)滿足Dini條件，T是帶有核K(x，y)且L2(Rn)有界的線性算子，滿足：

2）對于任意的 ||x-y＞2 ||x-x'＞0有

則K稱為θ型Calderón-Zygmund核，稱為θ型Calderón-Zygmund奇異積分算子。

因此，得到本文主要定理：

定理1設1＜p＜∞，w∈Ap，θ是連續模，并且T是θ型Calderón-Zygmund奇異積分算子，則T是Lp，κ(w)→Lp，κ(w)有界的。

為了證明該定理，需要如下引理。

引理1設w∈A2，函數θ是連續模，T是帶有核K(x，y)的θ型Calderón-Zygmund奇異積分算子，則有

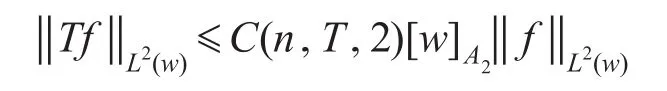
根據上面的結果，我們就可以通過外推法得到T的Lp(w)有界性，因此有必要介紹這一重要的定理，其證明可參考文獻[13-14]。

引理2設T是次線性算子，滿足存在p0:1＜p0＜∞使得對于任意的w∈Ap0有，則對任意的p:1＜p＜∞以及w∈Ap有

3 定理的證明

證明在方體3Q上考慮算子T的分解

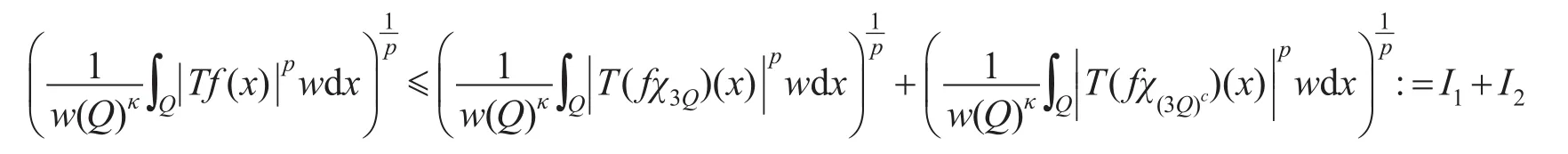
其中：χ3Q和χ(3Q)c為特征函數。

由引理1和引理2有

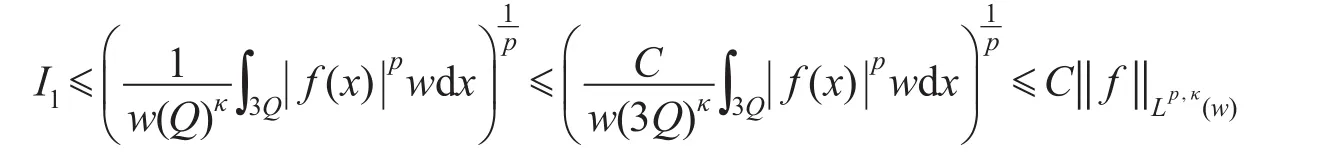
至于I2，取Rn中的范數為：，設Q的邊長為l，x0為Q的中心，由幾何關系知，對于任意的x∈Q以及y∈(3Q)c有。估計

對于任意的p＞1，取p0使得1＜p0＜p。由于存在，且，使得

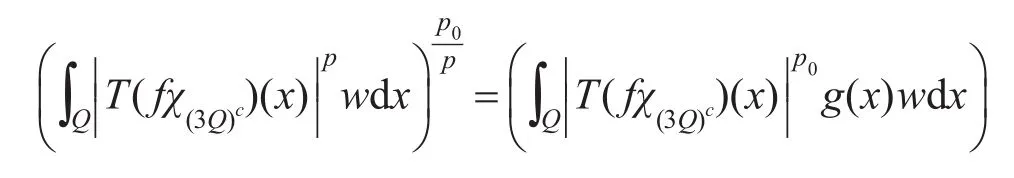
從而由H?lder不等式、Ap權定義有

結合前面I1的部分，從而有

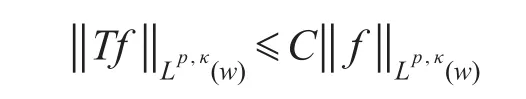
因此結論成立。

[1]MUCKENHOUPT B.Weighted norm inequalities for the Hardy maximal function[J].Trans.of the Amer Math Soc ，1972，165：207-226.

[2]KOMORI Y，SHIRAI S.Weighted Morrey spaces and a singular integral operator[J].Math Nachr，2009，282（2）：219-231.

[3]YE X F.Some estimates for multilinear commutators on the weighted Morrey spaces[J].Mathematical Sciences，2012，6（33），6-11.

[4]王華，劉和平.Bochner-Riesz算子在加權Morrey空間上的一些估計[J].數學學報，2012，55（3）：551-560.

[5]WANG H.The boundedness of some operators with rough kernel on the weighted Morrey spaces[EB/OL].（2010-11-26）[2013-01-07].http：//arxiv.org/pdf/1011.5763.

[6]WANG H.Some estimates for commutators of fractional integrals associated to operators with Gaussian kernel bounds on weighted Morrey spaces[EB/OL].（2012-08-15）[2013-01-07].http：//arxiv.org/abs/1202.5740.

[7]WANG H.Boundedness of fractional integral operators with rough kernels on weighted Morrey spaces[EB/OL].（2012-03-07）[2013-01-07].http：//arxiv.org/pdf/1203.1441.

[8]WANG H.Intrinsic square function on the weighted Morrey spaces[J].Journal of Mathematical Analysis and Applications.2012，396（1）：302-314.

[9]FU Z，LU S Z，SHI S G.Boundedness of sublinear operators on weighted Morrey spaces and applications[EB/OL].（2012-08-03）[2013-01-07].http：//arxiv.org/pdf/1208.4788.

[10]YABUTAK.Generaization of Calderón-Zygmund operator[J].Studia Math，1985，82：17-31.

[11]陳躍輝，葉曉峰，刁俊東.一類帶θ(t)型核的奇異積分算子的有界性[J].華東交通大學學報，2010，27（5）：81-84.

[12]HYT?NEN T.TheA2Theorem with the Dini condition[EB/OL].（2012-12-16）[2013-01-07].http：//arxiv.org/abs/1212.3842.

[13]GARCíAC J.An extrapolation theorem in the theory ofApweights[J].ProcAmer Math Soc，1983，87（3）：422-426.

[14]周民強.調和分析講義[M].北京：北京大學出版社1999：185-186.